Тригонометрические функции
Вариант 1
А. Выберите правильный ответ.
A1. Найдите область определения функции у = 2sin x + tg x.
1) х – любое число; 2) х R, кроме х=0; 3) х
R, кроме х=0; 3) х R, кроме
R, кроме  ;
;
4) х R, кроме х=1.
R, кроме х=1.
А2. Какими свойствами обладает функция у = 2 – sin 3x ?
1) нечетная, периодическая; 2) ни четная ни нечетная, непериодическая;
3) четная, периодическая; 4) ни четная ни нечетная, периодическая.
А3. Найдите все корни уравнения tg x = 1, принадлежащие промежутку [-; 2].
1) 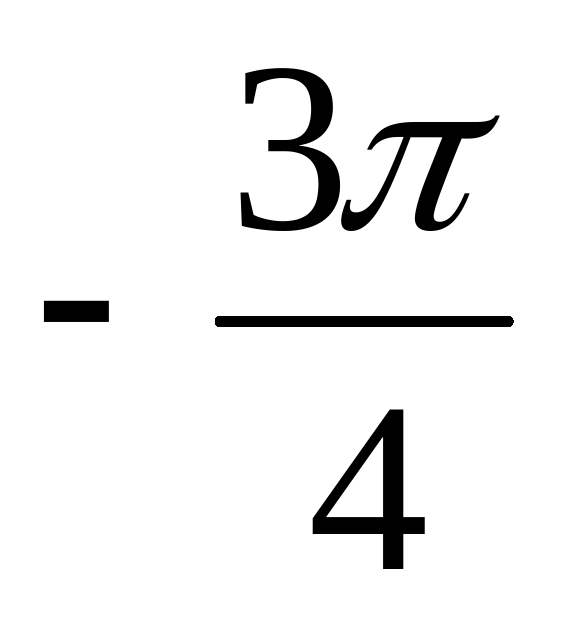 ;
; 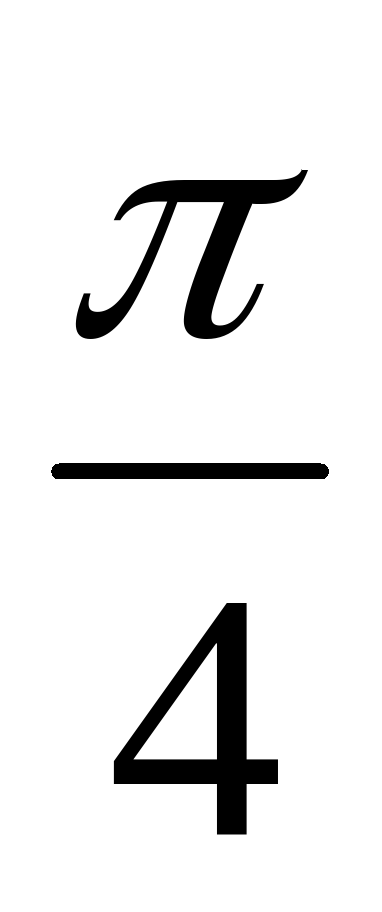 ;
;  ; 2)
; 2) 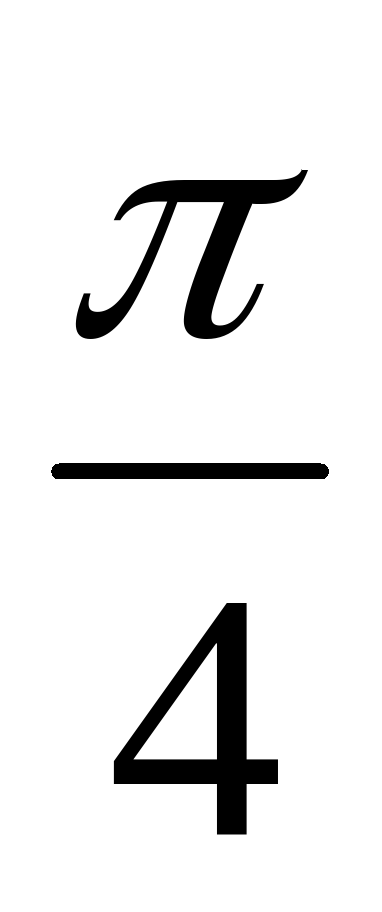 ;
; 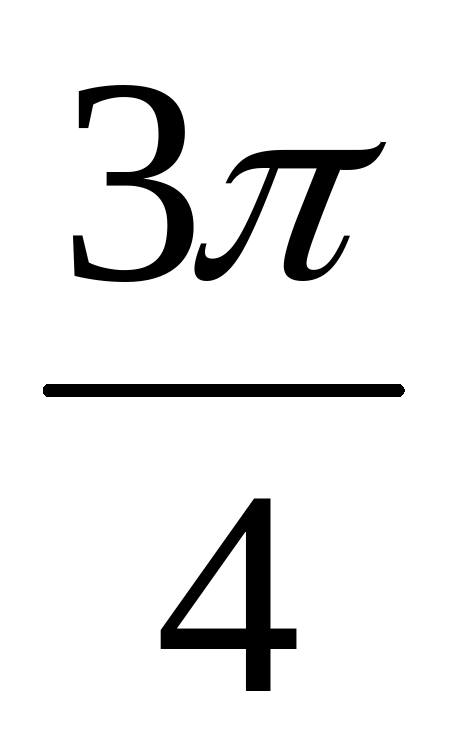 ;
;  ; 3)
; 3) 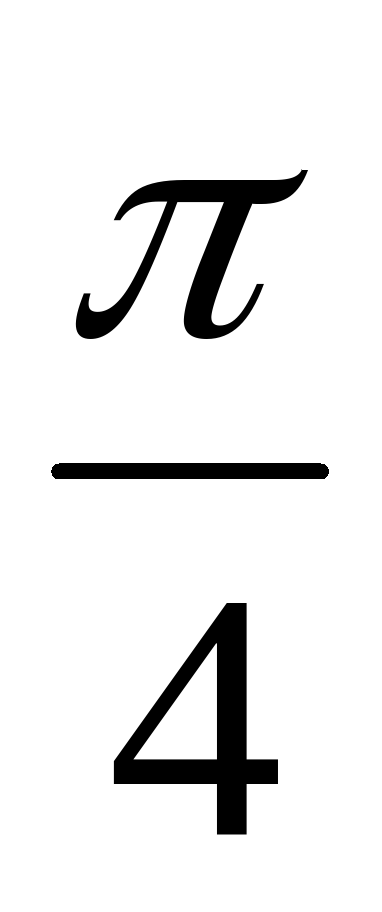 ;
;  ; 4)
; 4) 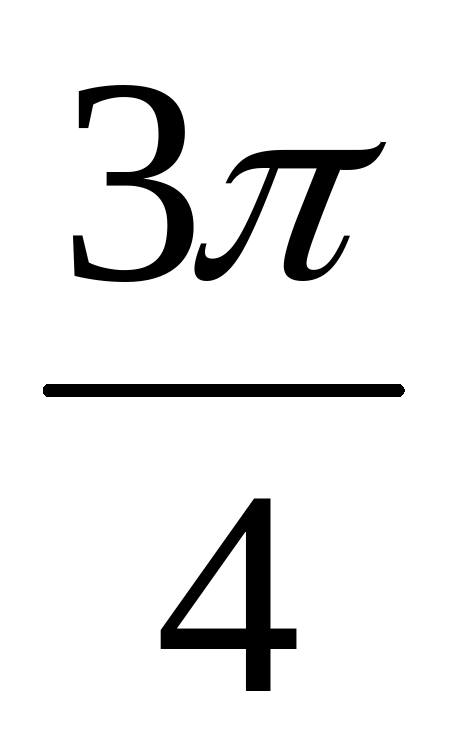 ;
;  ;
; 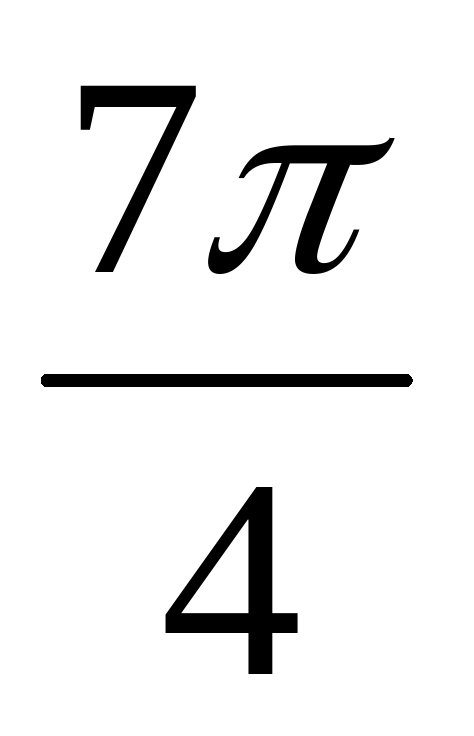 .
.
А4. Найдите наименьший положительный период функции у = 2sin 3x.
1) ; 2) 3; 3) 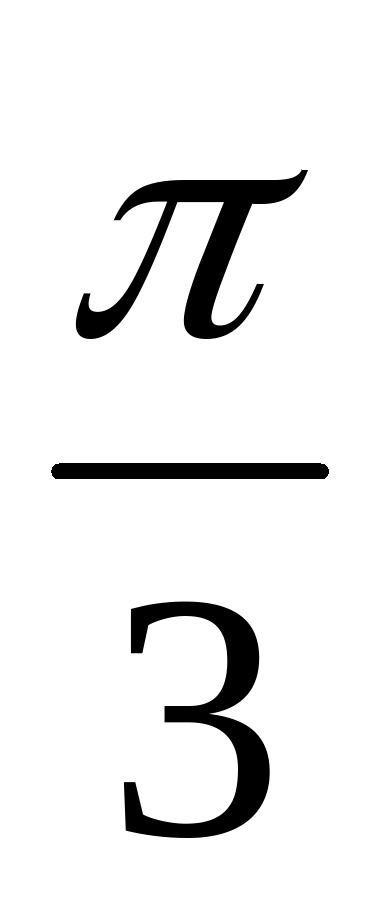 ; 4)
; 4) 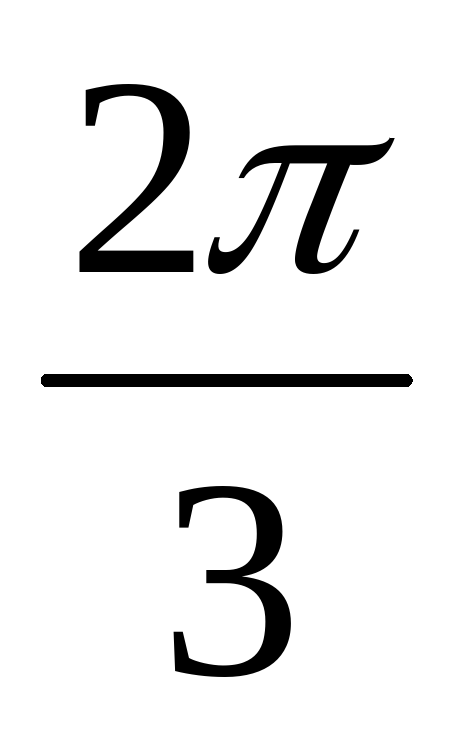 .
.
А5. Выберите верное неравенство:
1) tg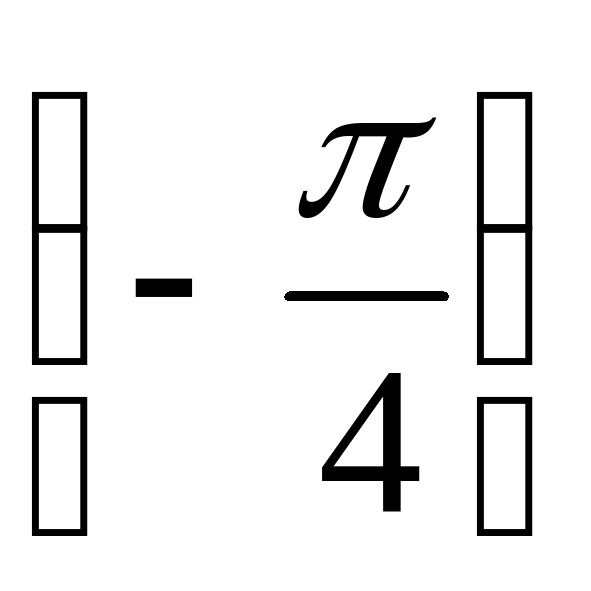
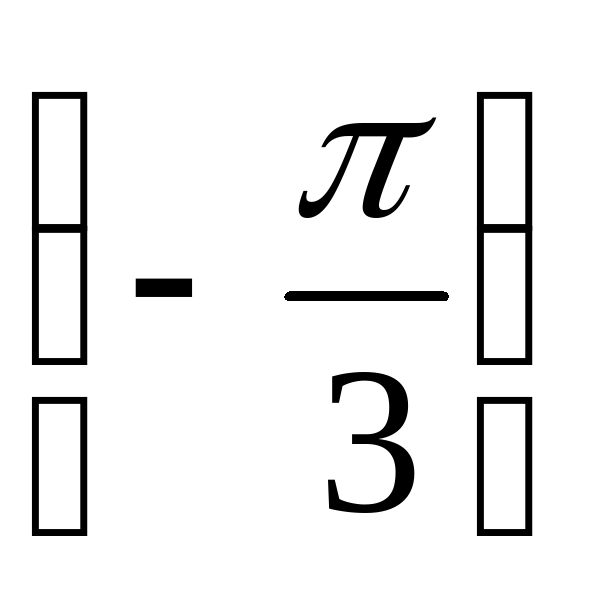 ; 2) tg
; 2) tg 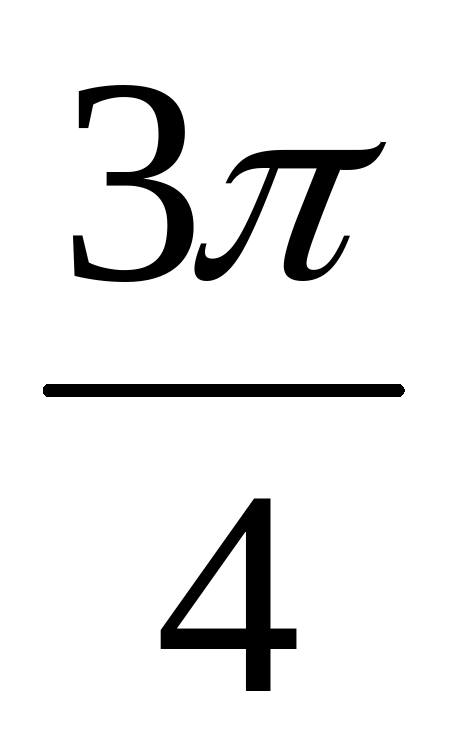
 ; 3) tg
; 3) tg 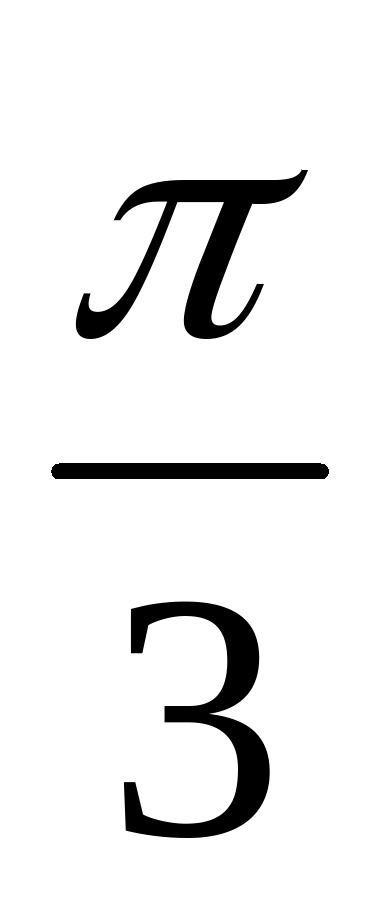 tg
tg 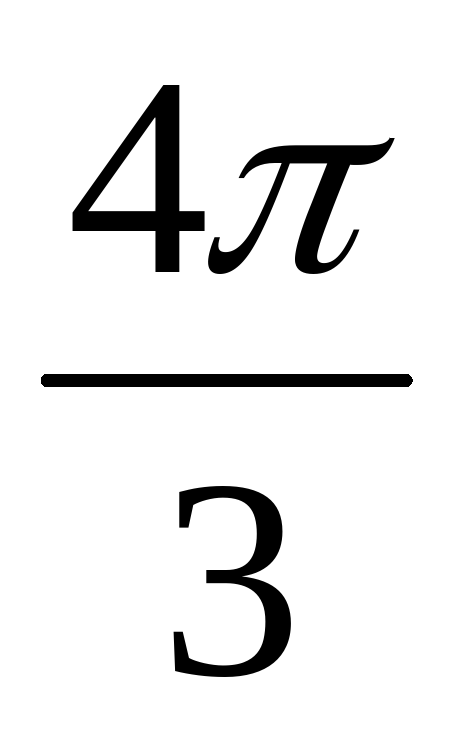 ; 4) tg
; 4) tg 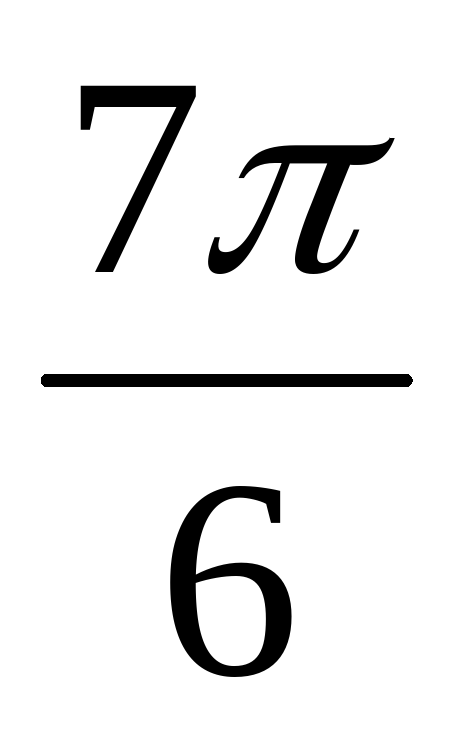
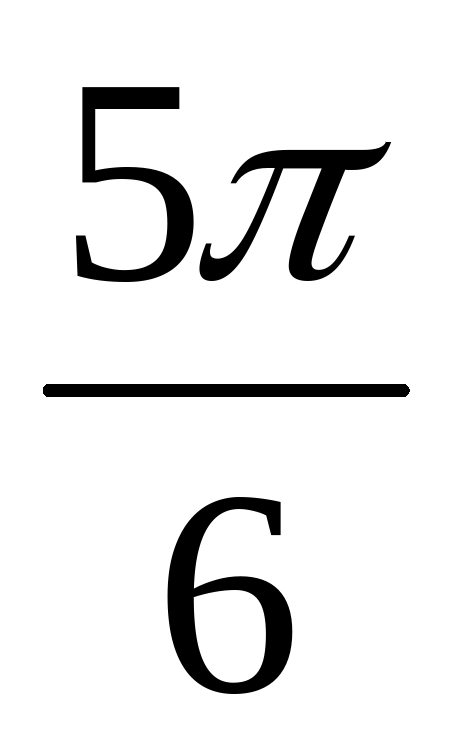 .
.
B. Запишите правильный ответ.
В1. Найдите длину отрезка, который является областью значений функции
В2. Найдите сумму всех корней уравнения , принадлежащие промежутку .
В3.Сколько целых чисел из промежутка принадлежит области определения функции ?
С. Для каждого задания приведите решение и укажите ответ.
С1. Найдите все значения х, при которых функция у = 1 – 2cos2 x принимает положительные значения.
С2. Найдите множество значений функции у = 2sin x , если х принадлежит промежутку .
С3. Постройте график функции у = |cos x|.
Нормы оценок: «3» - любые 4А «4» - 4А + 1В «5» - 3А + 2В + 1С
Тригонометрические функции
Вариант 2
А. Выберите правильный ответ.
A1. Найдите область определения функции .
1) х R; 2) х
R; 2) х R, кроме х=0; 3) х
R, кроме х=0; 3) х R, кроме
R, кроме  ; 4) х
; 4) х R, кроме х=1.
R, кроме х=1.
А2. Какими свойствами обладает функция у = 3x + cos x.
1) нечетная, периодическая; 2) ни четная ни нечетная, непериодическая;
3) четная, периодическая; 4) ни четная ни нечетная периодическая.
А3. Найдите все корни уравнения sin x = , принадлежащие промежутку[-;2].
1) 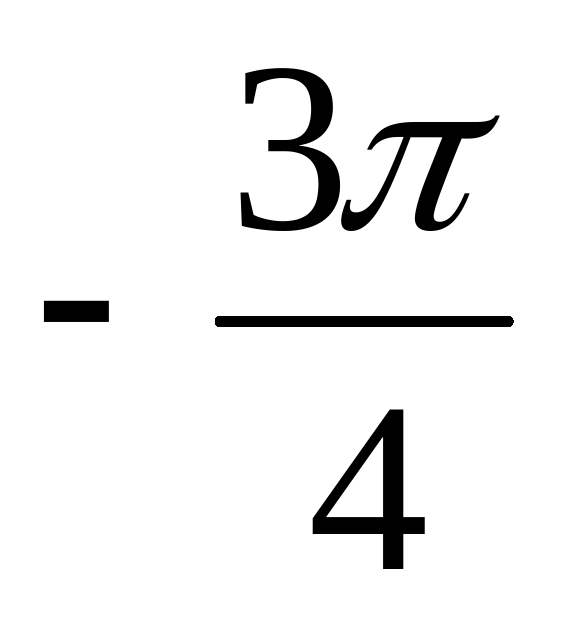 ;
; 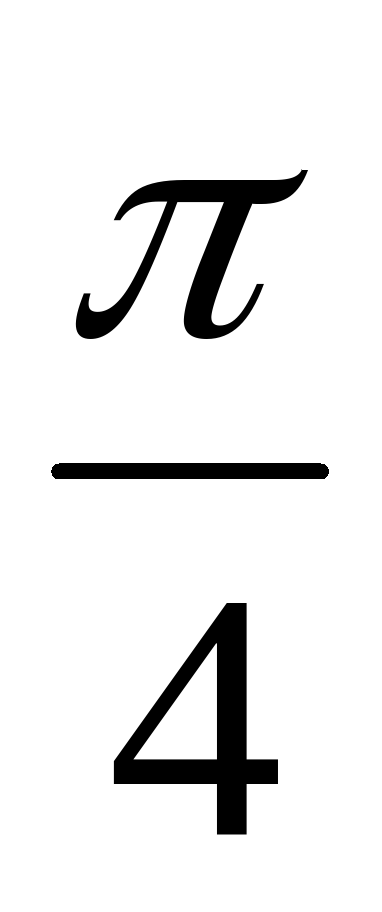 ;; 2)
;; 2) 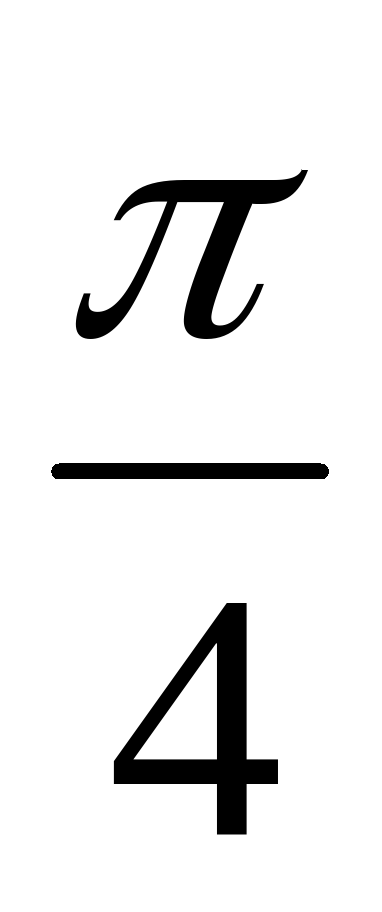 ;
; 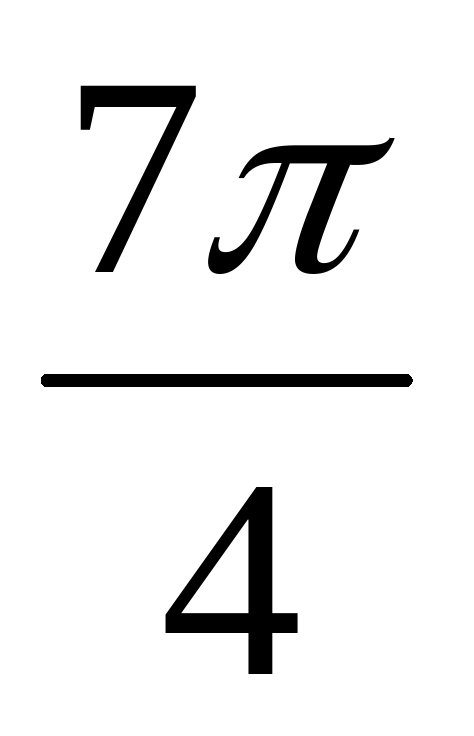 ; 3)
; 3) 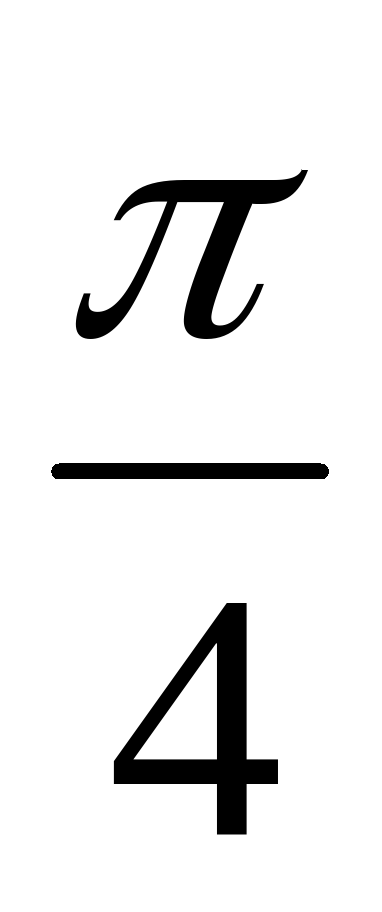 ;
;  ; 4)
; 4) 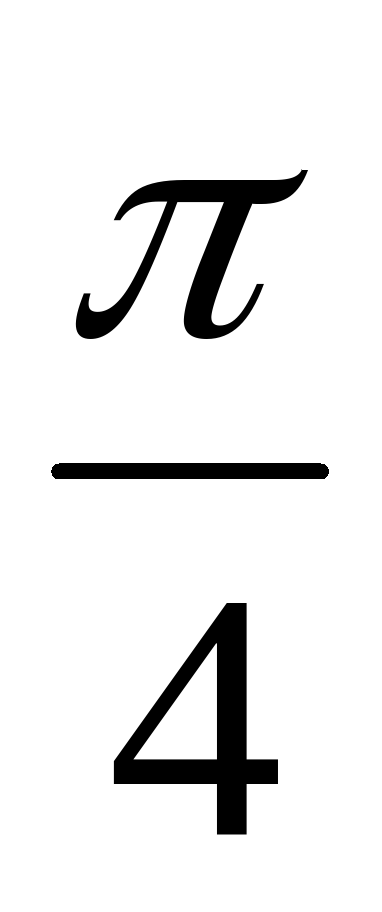 ;
;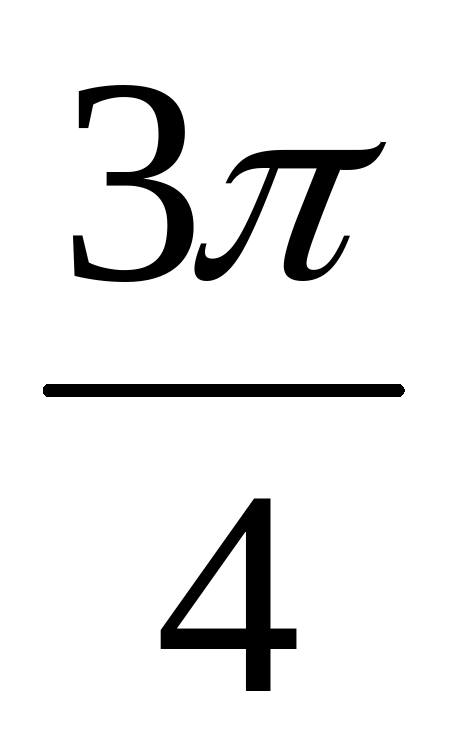 .
.
А4. Найдите наименьший положительный период функции у = 2sin .
1) 6; 2) 3; 3) 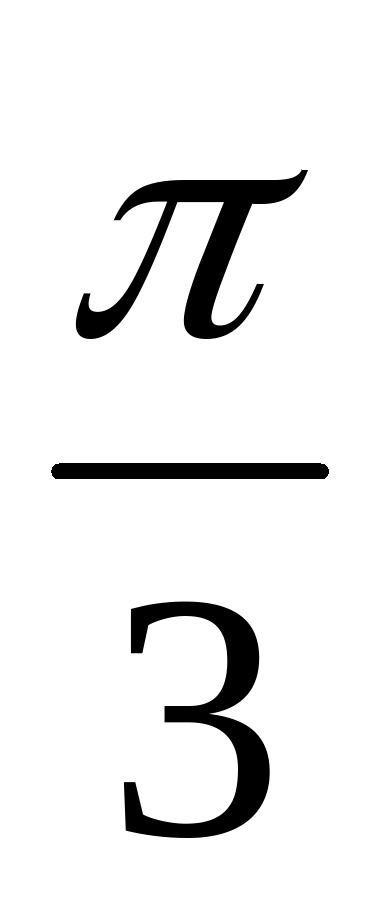 ; 4)
; 4) 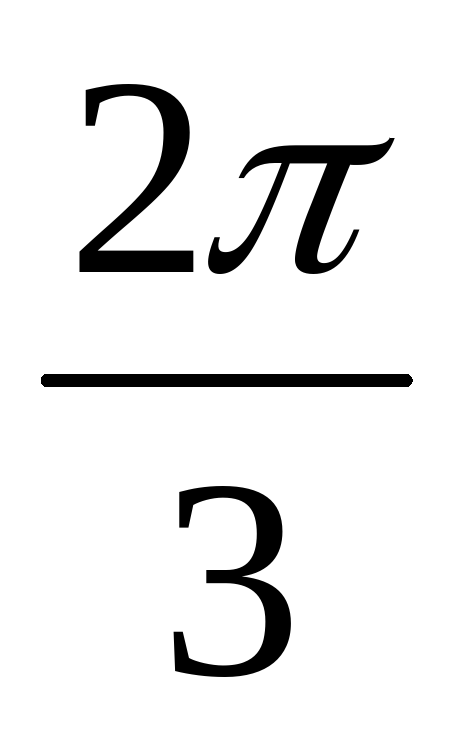 .
.
А5. Выберите верное неравенство:
1) sin  sin
sin  ; 2) sin
; 2) sin 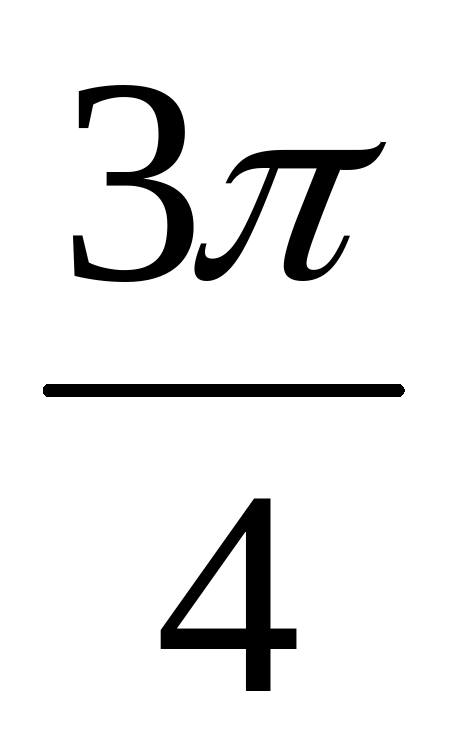 sin
sin  ; 3) sin
; 3) sin 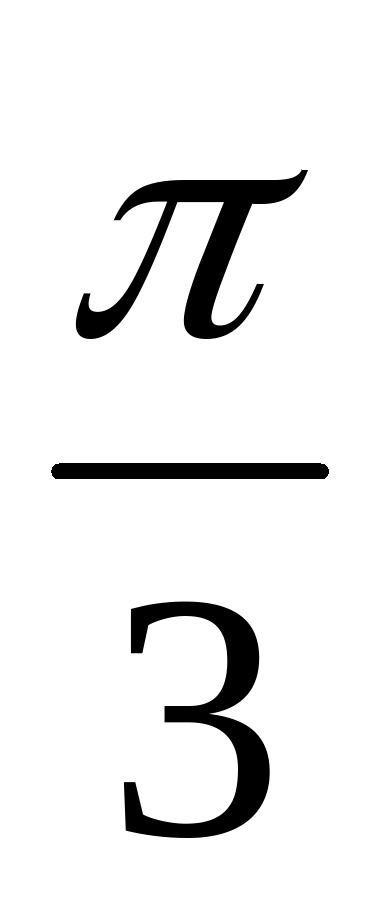 sin
sin 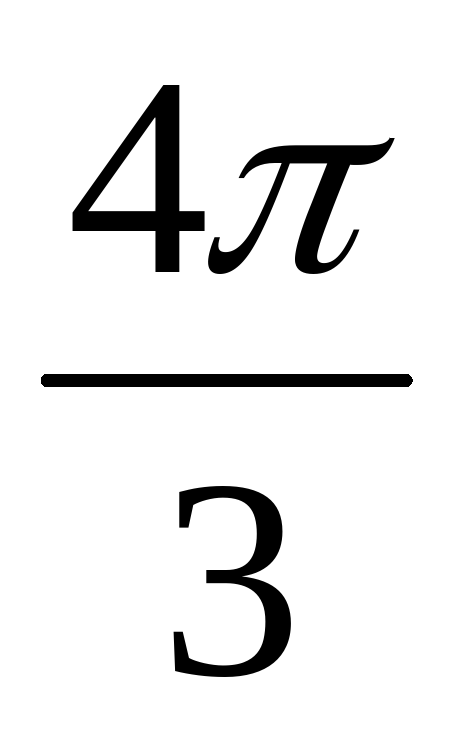 ; 4) sin
; 4) sin 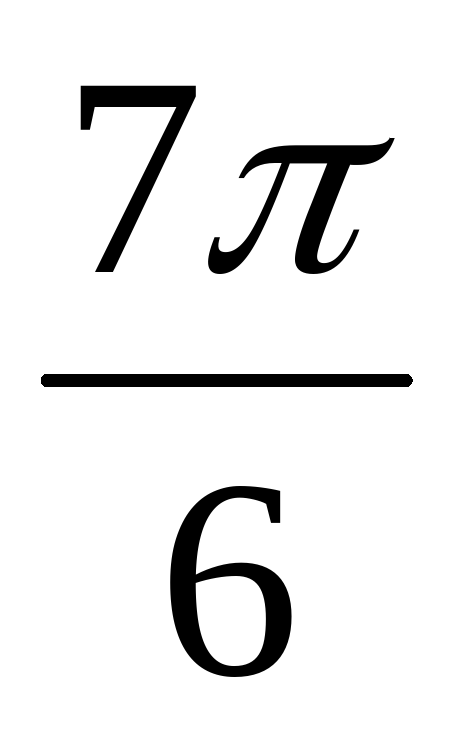 sin
sin 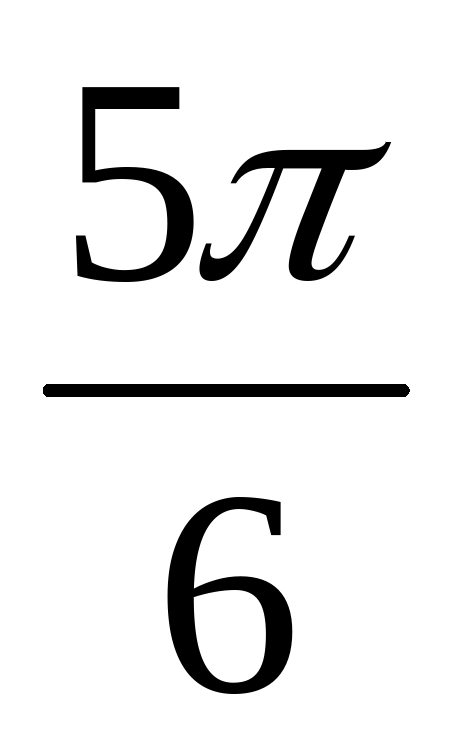 .
.
B. Запишите правильный ответ.
В1. Найдите длину отрезка, который является областью значений функции
В2. Найдите сумму всех корней уравнения , принадлежащие промежутку .
В3. Сколько целых чисел из промежутка принадлежит области определения функции ?
С. Для каждого задания приведите решение и укажите ответ.
С1. Найдите все значения х, при которых функция у = 1,5 – 2cos2 x принимает положительные значения.
С2. Найдите множество значений функции у = 6sin2 x – 8cos2 x .
С3. Постройте график функции у = tg |x|.
Нормы оценок: «3» - любые 4А «4» - 4А + 1В «5» - 3А + 2В + 1С
Тригонометрические функции
Вариант 3
А. Выберите правильный ответ.
A1. Найдите область определения функции у = 2sin x + tg x.
1) х – любое число; 2) х R, кроме х=0; 3) х
R, кроме х=0; 3) х R, кроме х=1;
R, кроме х=1;
4) х R, кроме
R, кроме  .
.
А2. Какими свойствами обладает функция у = 2 – sin 3x ?
1) ни четная ни нечетная, периодическая; 3) четная, периодическая;
2) ни четная ни нечетная, непериодическая; 4) нечетная, периодическая.
А3. Найдите все корни уравнения tg x = 1, принадлежащие промежутку [-; 2].
1) 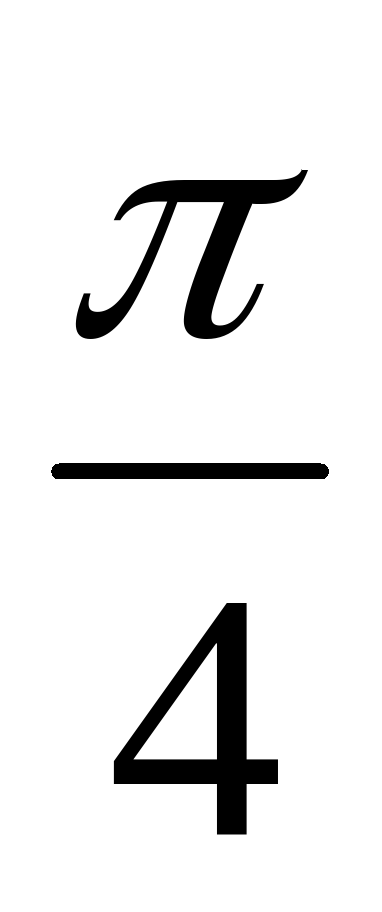 ;
;  ; 2)
; 2) 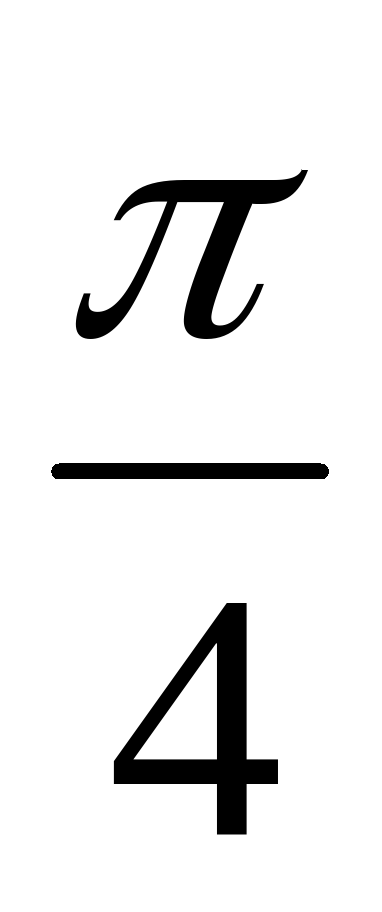 ;
; 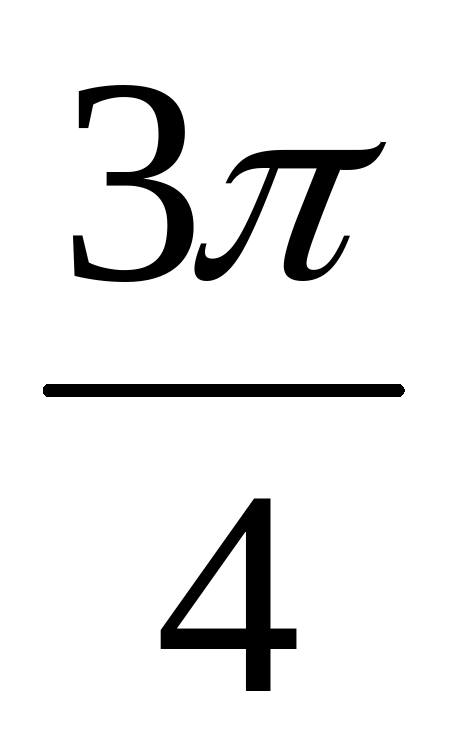 ;
;  ; 3)
; 3) 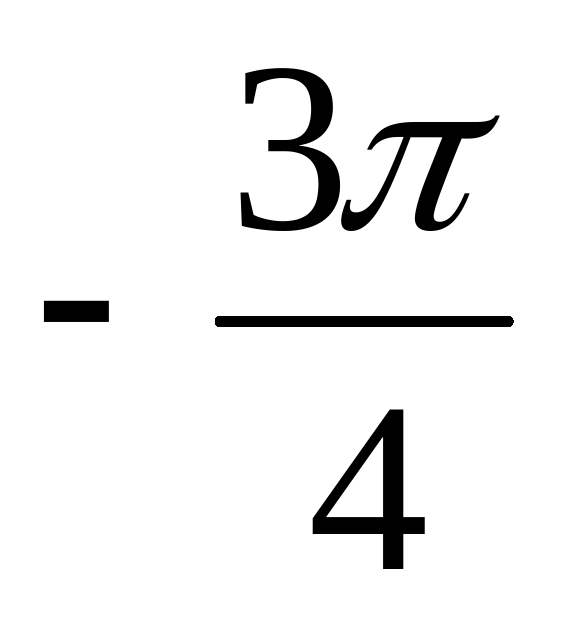 ;
; 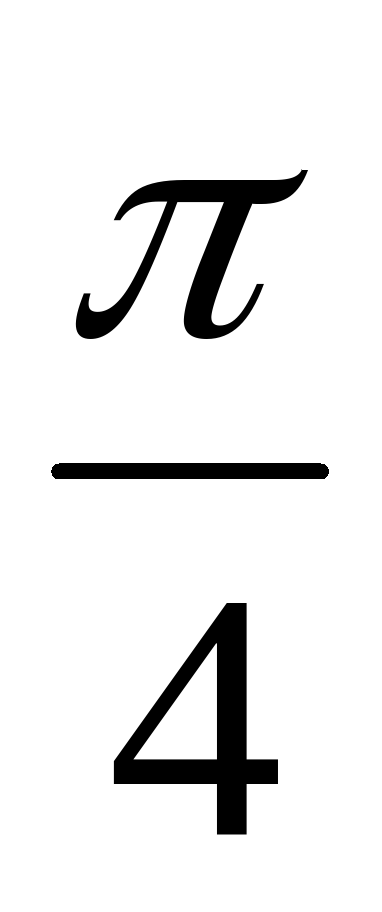 ;
;  ; 4)
; 4) 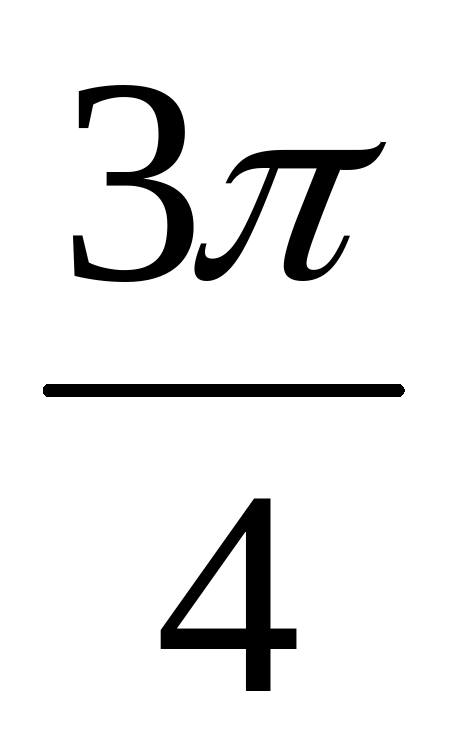 ;
;  ;
; 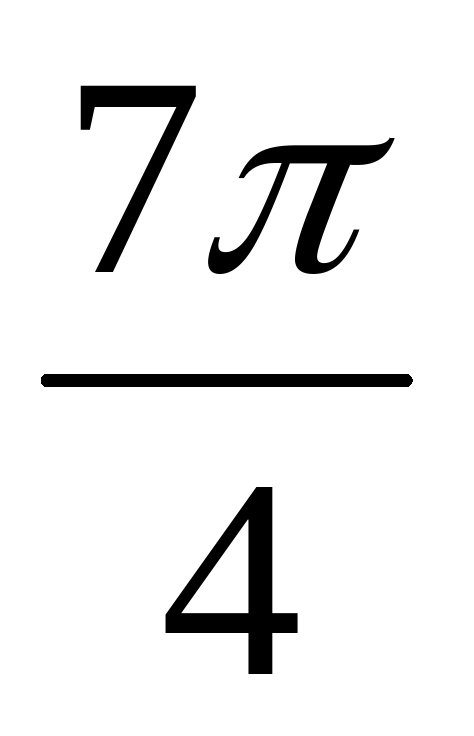 .
.
А4. Найдите наименьший положительный период функции у = 2sin 3x.
1) ; 2) 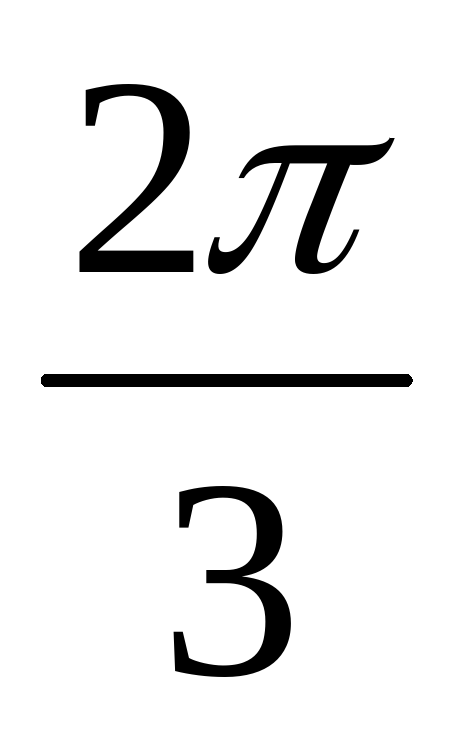 ; 3)
; 3) 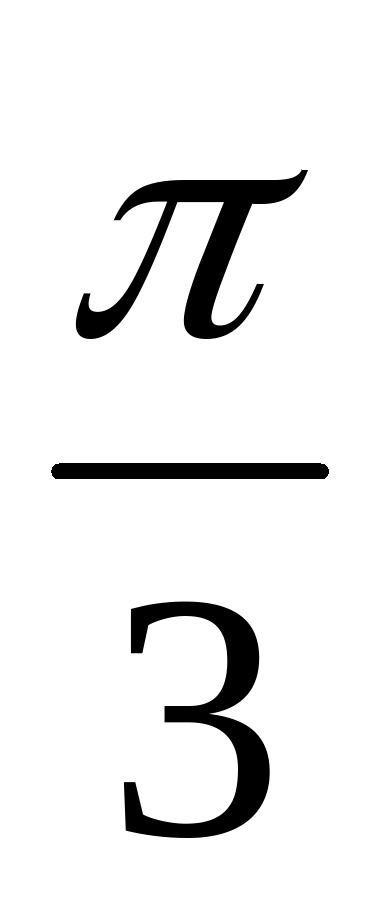 ; 4) 3.
; 4) 3.
А5. Выберите верное неравенство:
1) tg tg
tg ; 2) tg
; 2) tg 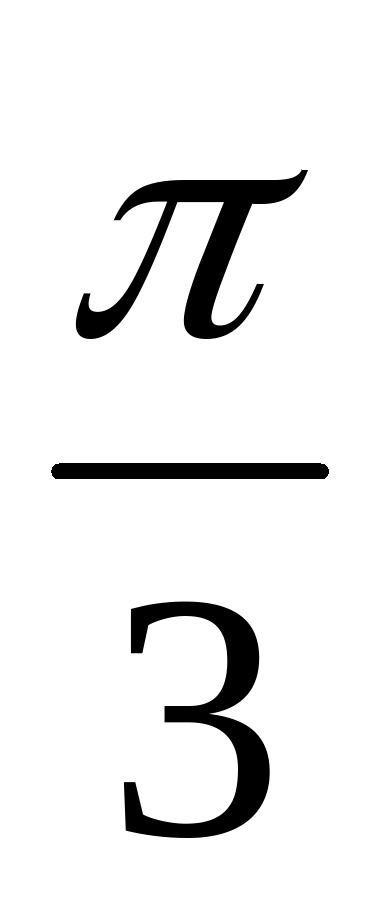 tg
tg 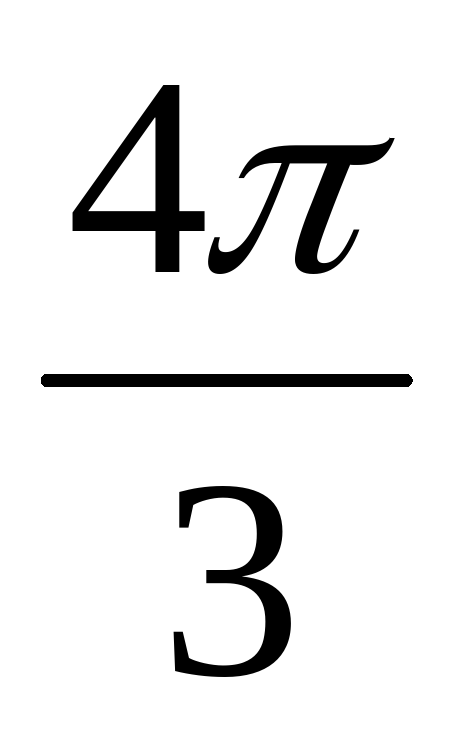 ; 3) tg
; 3) tg 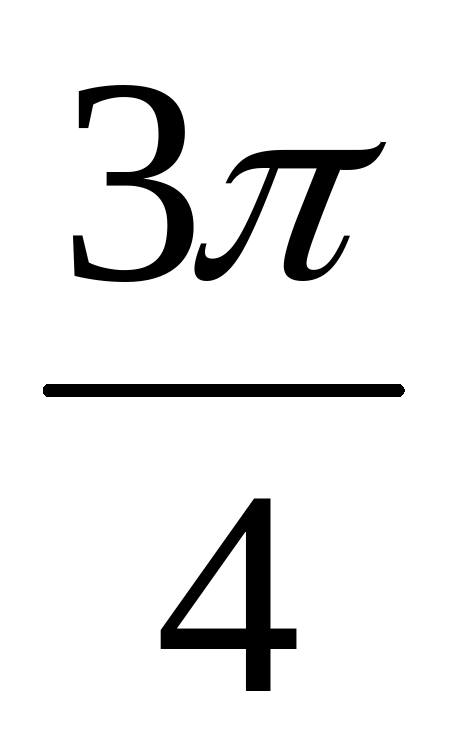 tg
tg  ; 4) tg
; 4) tg 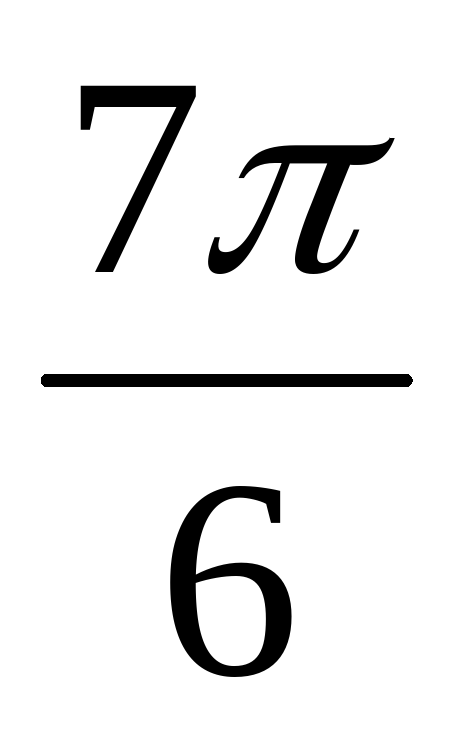 tg
tg 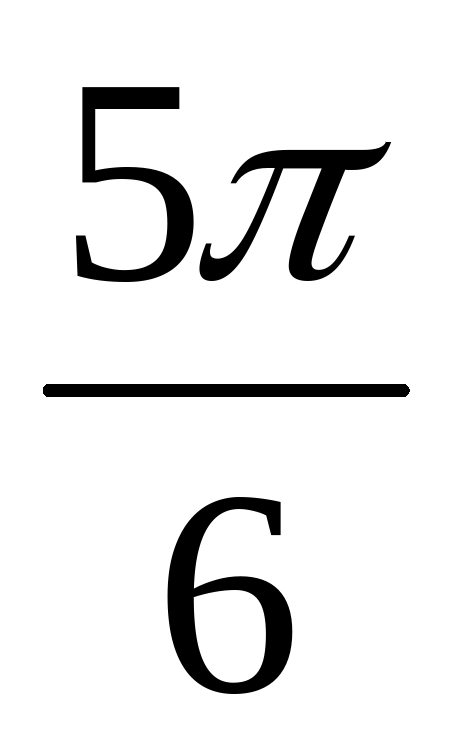 .
.
B. Запишите правильный ответ.
В1. Найдите длину отрезка, который является областью значений функции
В2. Найдите сумму всех корней уравнения , принадлежащие промежутку .
В3.Сколько целых чисел из промежутка принадлежит области определения функции ?
С. Для каждого задания приведите решение и укажите ответ.
С1. Найдите все значения х, при которых функция у = 1 – 2sin2 x принимает положительные значения.
С2. Найдите множество значений функции у = 2sin x , если х принадлежит промежутку .
С3. Постройте график функции у = |cos x|.
Нормы оценок: «3» - любые 4А «4» - 4А + 1В «5» - 3А + 2В + 1С
Тригонометрические функции
Вариант 4
А. Выберите правильный ответ.
A1. Найдите область определения функции .
1) х R, кроме х=0; 2) х
R, кроме х=0; 2) х R; 3) х
R; 3) х R, кроме
R, кроме  ; 4) х
; 4) х R, кроме х=1.
R, кроме х=1.
А2. Какими свойствами обладает функция у = 3x2 + cos x.
1) нечетная, периодическая; 2) ни четная ни нечетная, непериодическая;
3) четная, непериодическая; 4) ни четная ни нечетная периодическая.
А3. Найдите все корни уравнения sin x = , принадлежащие промежутку[-p;2p].
1) 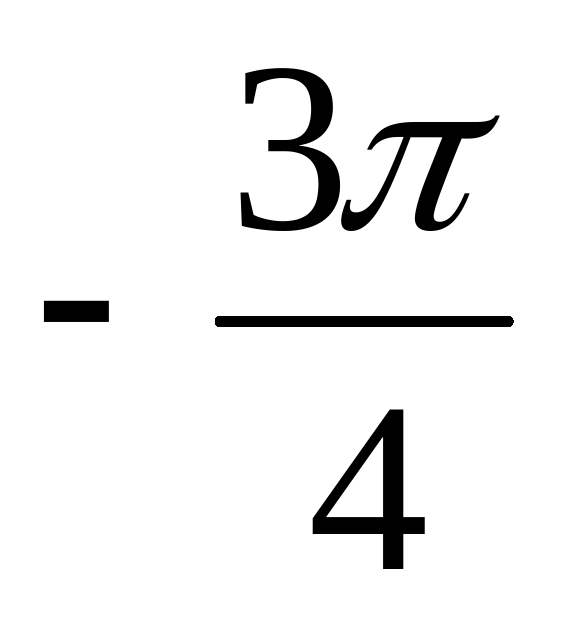 ;
; 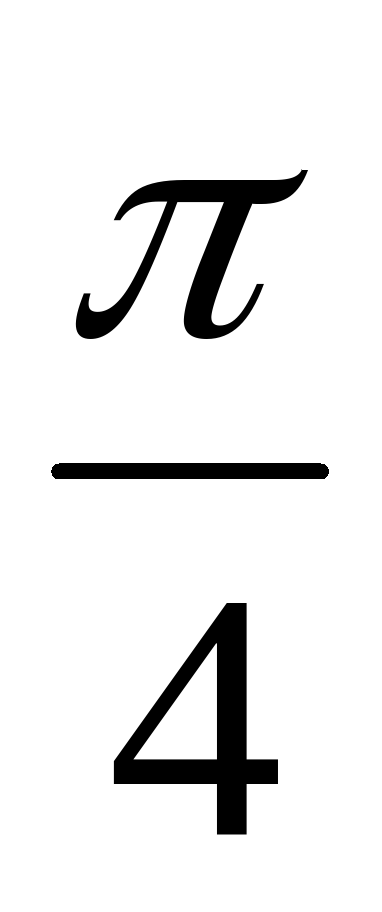 ;; 2)
;; 2) 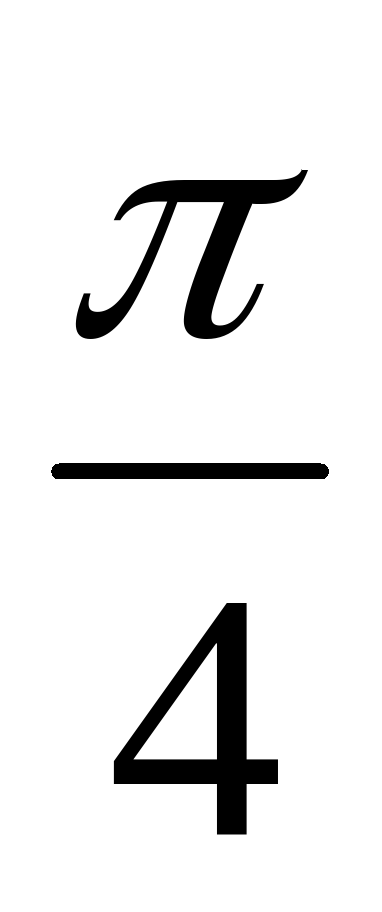 ;
;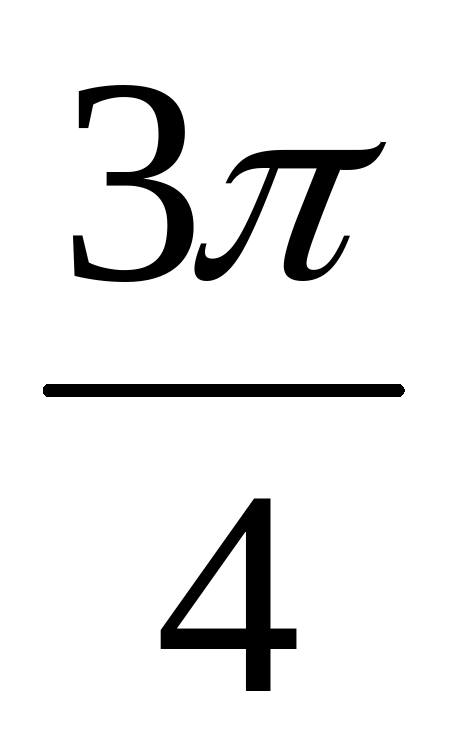 ; 3)
; 3) 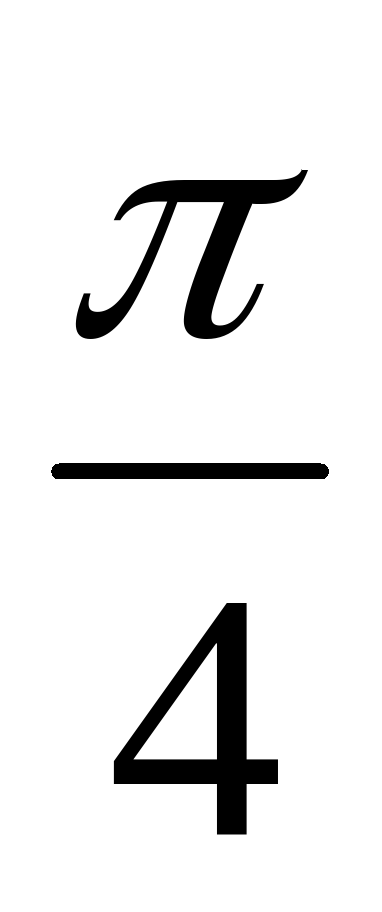 ;
;  ; 4)
; 4) 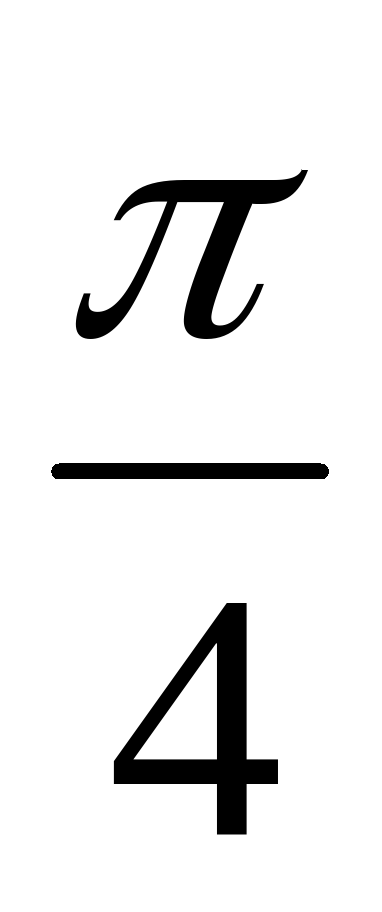 ;
;  .
.
А4. Найдите наименьший положительный период функции у = 2sin .
1) 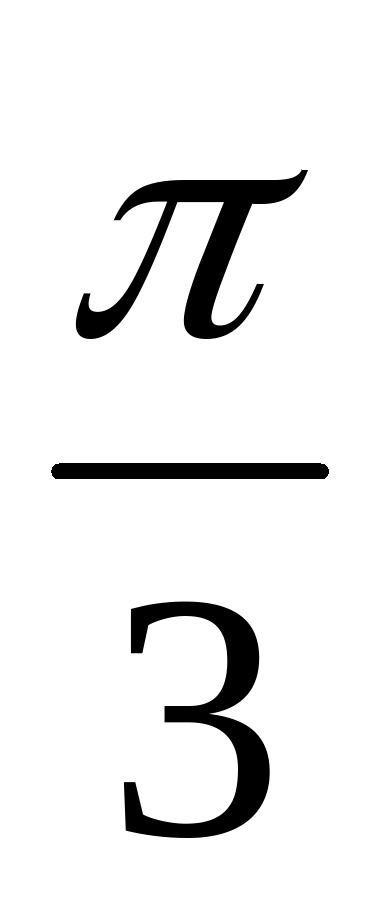 ; 2) 3p; 3) 6p; 4)
; 2) 3p; 3) 6p; 4) 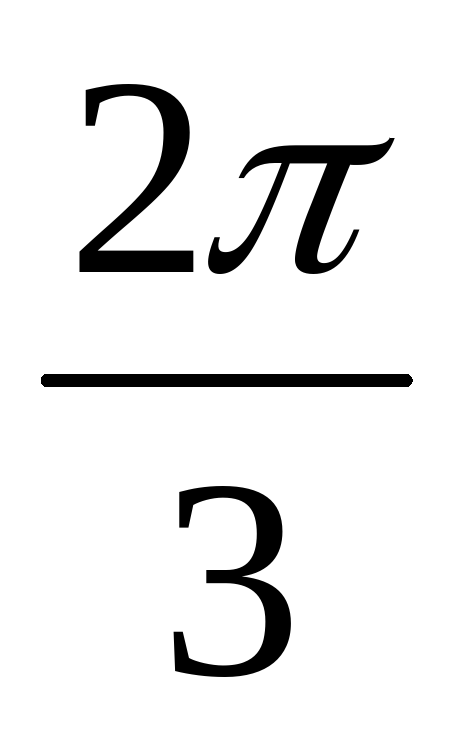 .
.
А5. Выберите верное неравенство:
1) sin 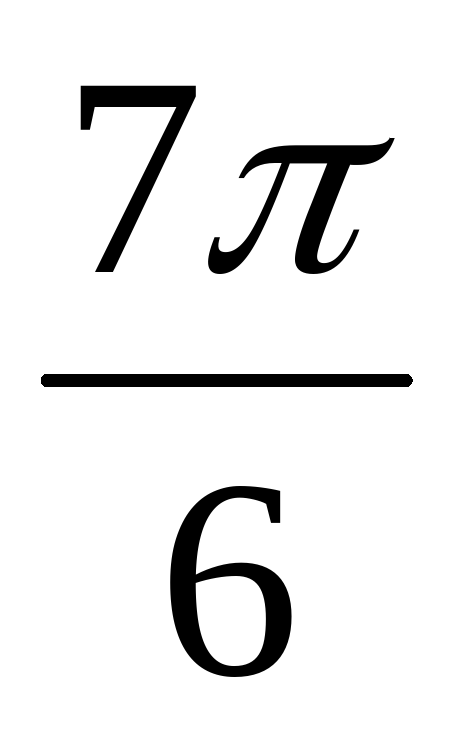 sin
sin 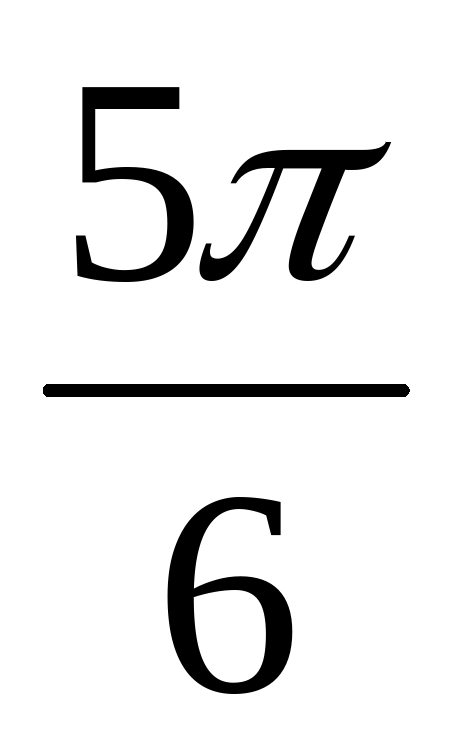 ; 2) sin
; 2) sin 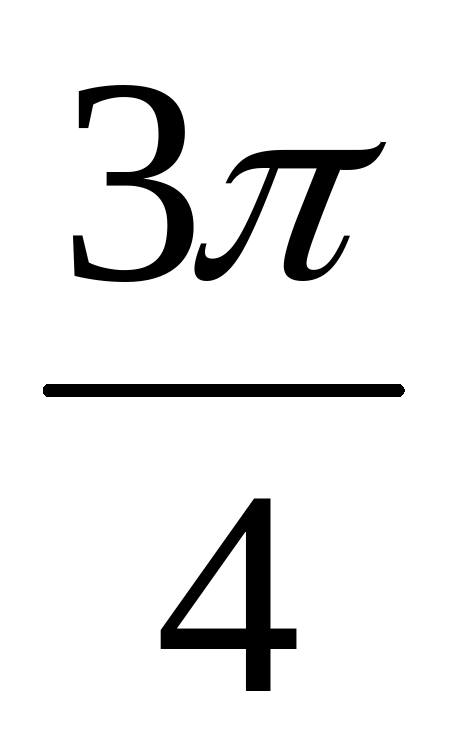 sin
sin  ; 3) sin
; 3) sin 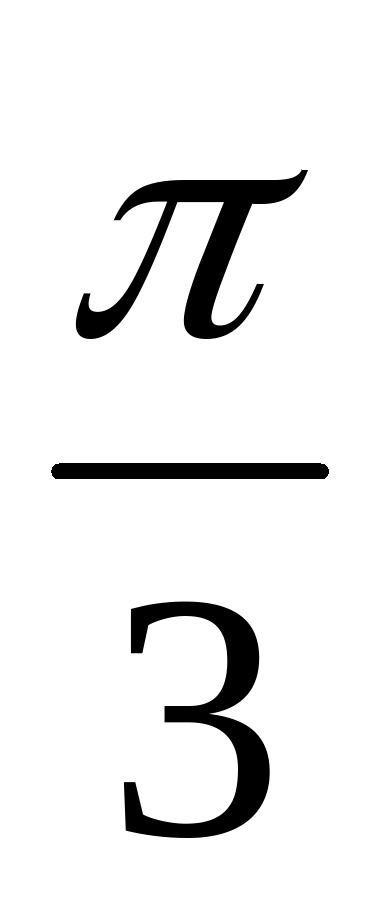 sin
sin 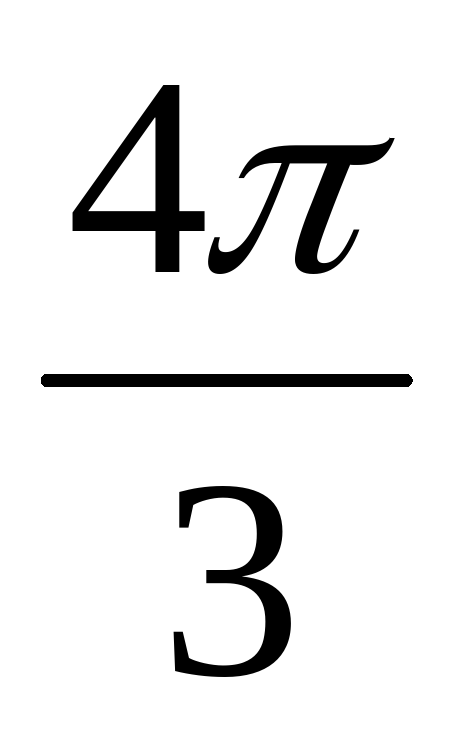 ; 4) sin
; 4) sin  sin
sin  .
.
B. Запишите правильный ответ.
В1. Найдите длину отрезка, который является областью значений функции
В2. Найдите сумму всех корней уравнения , принадлежащие промежутку .
В3. Сколько целых чисел из промежутка принадлежит области определения функции ?
С. Для каждого задания приведите решение и укажите ответ.
С1. Найдите все значения х, при которых функция у = 1,5 – 2cos2 x принимает положительные значения.
С2. Найдите множество значений функции у = 6sin2 x – 8cos2 x .
С3. Постройте график функции у = tg |x|.
Нормы оценок: «3» - любые 4А «4» - 4А + 1В «5» - 3А + 2В + 1С
Ответы к тестам «Тригонометрические функции»
| Вариант | А1 | А2 | А3 | А4 | А5 | В1 | В2 | В3 |
| 1 | 3 | 4 | 1 | 4 | 2 | 4 | | 5 |
| 1 | 2 | 2 | 4 | 1 | 1 | 4 | | 8 |
| 3 | 4 | 1 | 3 | 2 | 3 | 6 | | 6 |
| 4 | 1 | 3 | 2 | 3 | 4 | 2 | | 3 |


























