Тесты по математике
Тест знаний учащихся по теме: Первообразная и неопределённый
интеграл
Будет ли F(x) первообразной для функции f(x) на указанном промежутке:  ,
,
 , (-
, (- ; +
; + ).
).
а) да б) нет в) зависит от ситуации
Сопоставьте функцию и её первообразную:
| f(x) | F(x) |
| 1) 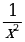 | а) 3x3 |
| 2) 0 | б) - cosx |
| 3) cos5x | в)  |
| 4) sinx | г) 4x +  + 5 + 5 |
| 5) 9x2 | д)  sin5x sin5x |
| 6) 4 +  x x | е) c |
1) - 4) -
2) - 5) -
3) - 6) -
Процесс отыскания функции по заданной производной называется:
а) дифференцированием;
б) интегрированием;
в) отысканием экстремума.
Верно ли рассуждение? Если да, то укажите правило, которым вы пользуетесь. Если нет, то укажите, в чём ошибка.
Найдём первообразную функции y=2xcosx. Первообразная для 2x – x2, для cosx – sinx. Значит первообразной для функции y=2xcosx будет служить функция y=x2sinx.
а) Да, используем правило___________________________________________
б) Нет, т.к._______________________________________________________________
Найдите первообразную для функции y=(4 – 5x)7
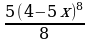 ;
;
 ;
;
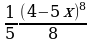 ;
;
 ;
;
7(4-5x)6;
-5∙7(4 -5x)6;
Продолжите фразу: первообразная суммы равна
а) сумме первообразных;
б) первообразной первой функции, умноженной на вторую функцию, плюс первообразная второй функции, в) умноженная на первую.
г) у этой фразы нет продолжения.
Заполните пропуски.
Если функция у=f(x) имеет на промежутке Х первообразную y=F(x), то___________________________________________________________________________________________________ называют неопределённым интегралом от функции y=f(x) и обозначают_______________.
Блок 1
1. Найдите общий вид первообразных для функции f
a) f(x)=2– х4 . Решение: воспользуемся правилами нахождения первообразных.
f(x) есть сумма двух функций y=2 и y= –x4, т.е. можно воспользоваться правилом нахождения первообразных №1(первообразная суммы равна сумме первообразных), для функции у=2 первообразной является у=2х, для того чтобы вычислить первообразную у функции у= –х4 необходимо воспользоваться правилом нахождения первообразных № 2(постоянный сомножитель можно вынести за знак первообразной), т.е. можно вынести -1, у функции у=х4 первообразной является функция у= ,следовательно у= –х4 имеет первообразную у= –
,следовательно у= –х4 имеет первообразную у= – , а функция f(x) имеет первообразную F(x)=2x–
, а функция f(x) имеет первообразную F(x)=2x– ; Ответ: F(x)=2x–
; Ответ: F(x)=2x– +С.
+С.
б) f(x)=  . Решение воспользуемся правилом нахождения первообразных №3 (если функция y=g(x) имеет первообразную y=G(x) ,то функция y=g(tx+m) имеет первообразную y=
. Решение воспользуемся правилом нахождения первообразных №3 (если функция y=g(x) имеет первообразную y=G(x) ,то функция y=g(tx+m) имеет первообразную y=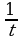 G(tx+m)), т.е. t= –15, m=4 , а g(x)=
G(tx+m)), т.е. t= –15, m=4 , а g(x)= , следовательно
, следовательно
F(x)=  . Ответ: F(x)=
. Ответ: F(x)= 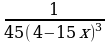 +С.
+С.
в) f(x)=  . Ответ: F(x)= –2tg(π/3–x);
. Ответ: F(x)= –2tg(π/3–x);
г) f(x)=7–3x+6x2–4x3. Ответ:F(x)=7x –1,5x2+2x3 –x4;
д) f(x)=2сos(2x–1). Ответ: F(x)= sin(2x-1).
2. Найдите неопределённый интеграл
a) 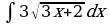 Решение: воспользуемся правилами нахождения неопределённого интеграла:
Решение: воспользуемся правилами нахождения неопределённого интеграла:  .
.
Ответ: 
б) 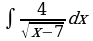 . Ответ: 8
. Ответ: 8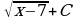 ; в)
; в) 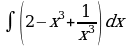 . Ответ: 2х –0,25х4 –0,5х –2+С;
. Ответ: 2х –0,25х4 –0,5х –2+С;
г)  ; Ответ: –0,25(3+8х)–2 –0,5sin2x; д)
; Ответ: –0,25(3+8х)–2 –0,5sin2x; д)  . Ответ: 0,5х2 –sinx –4x –4;
. Ответ: 0,5х2 –sinx –4x –4;
3. Вычислите интегралы: a)  . Решение: воспользуемся формулой Ньютона–Лейбница
. Решение: воспользуемся формулой Ньютона–Лейбница  .
. 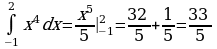 . Ответ:
. Ответ:  б)
б)  . Ответ: 1; в)
. Ответ: 1; в)  . Ответ: 20;
. Ответ: 20;
4. Вычислите площадь фигуры, ограниченной линиями y= , y=0, x=–1, x=1. Фигура ограниченная данными линиями является криволинейной трапецией и её площадь равна:
, y=0, x=–1, x=1. Фигура ограниченная данными линиями является криволинейной трапецией и её площадь равна:  Ответ: 0,4.
Ответ: 0,4.
Блок 1 Тест самоконтроля
1. Является ли функция F первообразной для функции f на указанном промежутке:
a) F(x)=3–sinx, f(x)=cosx, xÎ(- ;
;  );
);
б) F(x)=5– , f(x)= – 4
, f(x)= – 4 , xÎ(-
, xÎ(- ;
;  );
);
в) F(x)=соsx–4, f(x)= – sinx, xÎ(- ;
;  );
);
г) F(x)=3x+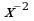 , f(x)=
, f(x)= 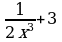 , xÎ(0;
, xÎ(0;  )?
)?
Ответ: нет, да, да, нет.
2. Правильно ли вычислены интегралы:
а)  ; б)
; б)  ; в)
; в) 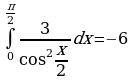 ; г)
; г)  ; д)
; д)  ?
?
Ответ: нет, да, нет, да, да.
3. Вычислите площадь фигуры, ограниченной линиями y=sinx, y=0, x=0, x=p.
Ответ:2.
4. Верны ли равенства:
а)  ; б)
; б)  ; в)
; в) 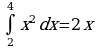 ;
;
г)  д)
д)  ;
;
е)  ?
?
Ответ: а) да; б) нет; в) нет; г) нет; д) да; е) нет.
Тест знаний учащихся по теме: Первообразная и неопределённый интеграл
Будет ли F(x) первообразной для функции f(x) на указанном промежутке:  ,
,
 , (-
, (- ; +
; + ).
).
а) да б) нет в) зависит от ситуации
Сопоставьте функцию и её первообразную:
| f(x) | F(x) |
| 1) 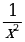 | а) 3x3 |
| 2) 0 | б) - cosx |
| 3) cos5x | в)  |
| 4) sinx | г) 4x +  + 5 + 5 |
| 5) 9x2 | д)  sin5x sin5x |
| 6) 4 +  x x | е) c |
1) - 4) -
2) - 5) -
3) - 6) -
Процесс отыскания функции по заданной производной называется:
а) дифференцированием;
б) интегрированием;
в) отысканием экстремума.
Верно ли рассуждение? Если да, то укажите правило, которым вы пользуетесь. Если нет, то укажите, в чём ошибка.
Найдём первообразную функции y=2xcosx. Первообразная для 2x – x2, для cosx – sinx. Значит первообразной для функции y=2xcosx будет служить функция y=x2sinx.
а) Да, используем правило___________________________________________
б) Нет, т.к._______________________________________________________________
Найдите первообразную для функции y=(4 – 5x)7
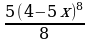 ;
;
 ;
;
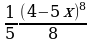 ;
;
 ;
;
7(4-5x)6;
-5∙7(4 -5x)6;
Продолжите фразу: первообразная суммы равна
а) сумме первообразных;
б) первообразной первой функции, умноженной на вторую функцию, плюс первообразная второй функции, в) умноженная на первую.
г) у этой фразы нет продолжения.
Заполните пропуски.
Если функция у=f(x) имеет на промежутке Х первообразную y=F(x), то___________________________________________________________________________________________________ называют неопределённым интегралом от функции y=f(x) и обозначают_______________
Тест знаний учащихся по теме определённый интеграл
Определенным интегралом от функции y =f(x) по отрезку [a;b] называют:
 , где
, где  и
и 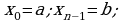
число равное F(b) - F(a)
F(x)+C

Запишите формулу Ньютона-Лейбница______________________
Геометрический смысл определённого интеграла состоит в следующем:
перемещение точки;
угол наклона касательной;
ограничивает криволинейную трапецию;
площадь криволинейной трапеции
Верно ли записано утверждение: для любой функции f(x) на отрезке [a,b] справедливо равенство: 
да;
нет;
не знаю.
Допишите свойства определённого интеграла
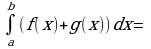
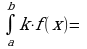
Если а, то
Площадь фигуры, ограниченной линиями x = a и x = b, и графиками функции у =f(x), y =g(x), непрерывных на отрезке [b, a] и таких, что для всех x из этого отрезка выполняется неравенство f(x)≤g(x), вычисляется по формуле:
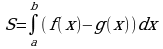



нет правильного ответа
Блок 1
1. Найдите общий вид первообразных для функции f
a) f(x)=2– х4 . Решение: воспользуемся правилами нахождения первообразных.
f(x) есть сумма двух функций y=2 и y= –x4, т.е. можно воспользоваться правилом нахождения первообразных №1(первообразная суммы равна сумме первообразных), для функции у=2 первообразной является у=2х, для того чтобы вычислить первообразную у функции у= –х4 необходимо воспользоваться правилом нахождения первообразных № 2(постоянный сомножитель можно вынести за знак первообразной), т.е. можно вынести -1, у функции у=х4 первообразной является функция у= ,следовательно у= –х4 имеет первообразную у= –
,следовательно у= –х4 имеет первообразную у= – , а функция f(x) имеет первообразную F(x)=2x–
, а функция f(x) имеет первообразную F(x)=2x– ; Ответ: F(x)=2x–
; Ответ: F(x)=2x– +С.
+С.
б) f(x)=  . Решение воспользуемся правилом нахождения первообразных №3 (если функция y=g(x) имеет первообразную y=G(x) ,то функция y=g(tx+m) имеет первообразную y=
. Решение воспользуемся правилом нахождения первообразных №3 (если функция y=g(x) имеет первообразную y=G(x) ,то функция y=g(tx+m) имеет первообразную y=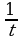 G(tx+m)), т.е. t= –15, m=4 , а g(x)=
G(tx+m)), т.е. t= –15, m=4 , а g(x)= , следовательно
, следовательно
F(x)=  . Ответ: F(x)=
. Ответ: F(x)= 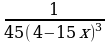 +С.
+С.
в) f(x)=  . Ответ: F(x)= –2tg(π/3–x);
. Ответ: F(x)= –2tg(π/3–x);
г) f(x)=7–3x+6x2–4x3. Ответ:F(x)=7x –1,5x2+2x3 –x4;
д) f(x)=2сos(2x–1). Ответ: F(x)= sin(2x-1).
2. Найдите неопределённый интеграл
a) 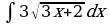 Решение: воспользуемся правилами нахождения неопределённого интеграла:
Решение: воспользуемся правилами нахождения неопределённого интеграла:  .
.
Ответ: 
б) 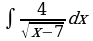 . Ответ: 8
. Ответ: 8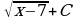 ; в)
; в) 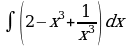 . Ответ: 2х –0,25х4 –0,5х –2+С;
. Ответ: 2х –0,25х4 –0,5х –2+С;
г)  ; Ответ: –0,25(3+8х)–2 –0,5sin2x; д)
; Ответ: –0,25(3+8х)–2 –0,5sin2x; д)  . Ответ: 0,5х2 –sinx –4x –4;
. Ответ: 0,5х2 –sinx –4x –4;
3. Вычислите интегралы: a)  . Решение: воспользуемся формулой Ньютона–Лейбница
. Решение: воспользуемся формулой Ньютона–Лейбница  .
. 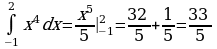 . Ответ:
. Ответ:  б)
б)  . Ответ: 1; в)
. Ответ: 1; в)  . Ответ: 20;
. Ответ: 20;
4. Вычислите площадь фигуры, ограниченной линиями y= , y=0, x=–1, x=1. Фигура ограниченная данными линиями является криволинейной трапецией и её площадь равна:
, y=0, x=–1, x=1. Фигура ограниченная данными линиями является криволинейной трапецией и её площадь равна:  Ответ: 0,4.
Ответ: 0,4.
Блок 1 Тест самоконтроля
1. Является ли функция F первообразной для функции f на указанном промежутке:
a) F(x)=3–sinx, f(x)=cosx, xÎ(- ;
;  );
);
б) F(x)=5– , f(x)= – 4
, f(x)= – 4 , xÎ(-
, xÎ(- ;
;  );
);
в) F(x)=соsx–4, f(x)= – sinx, xÎ(- ;
;  );
);
г) F(x)=3x+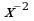 , f(x)=
, f(x)= 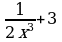 , xÎ(0;
, xÎ(0;  )?
)?
Ответ: нет, да, да, нет.
2. Правильно ли вычислены интегралы:
а)  ; б)
; б)  ; в)
; в) 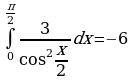 ; г)
; г)  ; д)
; д)  ?
?
Ответ: нет, да, нет, да, да.
3. Вычислите площадь фигуры, ограниченной линиями y=sinx, y=0, x=0, x=p.
Ответ:2.
4. Верны ли равенства:
а)  ; б)
; б)  ; в)
; в) 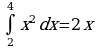 ;
;
г)  д)
д)  ;
;
е)  ?
?
Ответ: а) да; б) нет; в) нет; г) нет; д) да; е) нет.
Блок 1 Контрольный тест Вариант 1
1. Найдите неопределённый интеграл:
а) 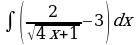 ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д) 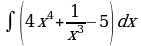 ; е)
; е)  .
.
2. Вычислите интегралы:
а) 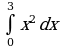 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
3. Вычислите площадь фигуры, ограниченной линиями:
а) y=1– x3, y=0, x=0;
б) y=sinx, y=0, x=p/6, x=p/3.
Блок 1 Контрольный тест Вариант 2
1. Найдите неопределённый интеграл:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е)  .
.
2. Вычислите интегралы:
а)  ; б)
; б) 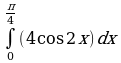 ; в)
; в)  ; г)
; г)  ;
;
3. Вычислите площадь фигуры, ограниченной линиями:
а) y= x4, y=1;
б) y=2sinx, y=0, x=p/6, x=p/3.
Блок 2 Задачи
1. Найдите неопределённый интеграл:
а)  . Решение: заметим, что подынтегральная функция не является функцией из таблицы в явном виде, поэтому её необходимо преобразовать:
. Решение: заметим, что подынтегральная функция не является функцией из таблицы в явном виде, поэтому её необходимо преобразовать: 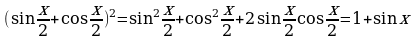 , интеграл от полученной функции легко вычисляется:
, интеграл от полученной функции легко вычисляется:  . Ответ:
. Ответ:  +С.
+С.
б) 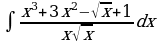 . Решение: аналогично примеру под буквой а) упрощаем подынтегральную функцию и вычисляем интеграл:
. Решение: аналогично примеру под буквой а) упрощаем подынтегральную функцию и вычисляем интеграл:  .
.
Ответ: 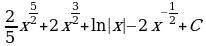 .
.
2. Для функции f(х)=2cosx найти первообразную, график которой проходит через точку М(–0,5p;1). Решение: Найдём множество первообразных функции f(x), F(x)=2sinx+C, известно что график первообразной проходит через точку M, значит F(-0,5π)=1, но F(x)=2sinx+C, следовательно 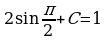 , откуда С= –1. Ответ: F(x)=2sinx –1.
, откуда С= –1. Ответ: F(x)=2sinx –1.
3. Вычислите интеграл:
 ; Решение: упрощаем подынтегральную функцию и вычисляем определённый интеграл:
; Решение: упрощаем подынтегральную функцию и вычисляем определённый интеграл:  . Ответ:
. Ответ: 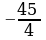 .
.
4. Вычислите площадь фигуры, ограниченной линиями:
а) y= (x+2)2, y=0, x=0. Решение: площадь искомой фигуры является площадью соответствующей криволинейной трапеции, которую можно вычислить с помощью определённого интеграла, нижний предел интегрирования равен –2 т.к. в точке
(–2;0) график функции пересекает прямую у=0, верхний предел интегрирования равен 0, т.к. фигура ограничена прямой х=0. 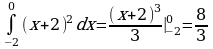 .
.
Ответ:  .
.
Блок 2 Тест самоконтроля
1. Является ли функция F первообразной для функции f на указанном промежутке:
a) F(x)=2x +cos , f(x)= 2 –
, f(x)= 2 –  sin
sin , xÎ(-
, xÎ(- ;
;  ); б) F(x)=
); б) F(x)= , f(x)= –
, f(x)= –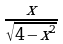 , xÎ(-2;2);
, xÎ(-2;2);
в) F(x)= 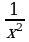 , f(x)=
, f(x)= 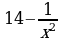 , xÎ(0;
, xÎ(0;  ); г) F(x)=
); г) F(x)= 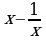 , f(x)=
, f(x)= 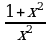 , xÎ(0;
, xÎ(0;  )?
)?
Ответ: да, да, нет, да.
2. Для функции f(х)= найдите первообразную, график которой
найдите первообразную, график которой
проходит через точку М(4;5):
а) F(х)= +3; б) F(х)=2
+3; б) F(х)=2 +1; в) F(х)=2
+1; в) F(х)=2 +3; г) F(х)=
+3; г) F(х)= +5.
+5.
Ответ: б)
3.Верны ли равенства:
а)  ; б)
; б) ; в)
; в) ;
;
г)  ; д)
; д) ?
?
Ответ: да, да, да, нет, да.
Блок 2 Контрольный тест Вариант 1
1. Найдите неопределённый интеграл:
а)  ; б)
; б) ; в)
; в) 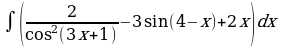 ; г)
; г)  ;
;
д)  .
.
2. Графики первообразных F1 и F2 функции f(x)=3x2 –2x+4 проходят через точки М(–1;1) и N(0;3). Какова разность этих двух первообразных? Какой из графиков F1 и F2 расположен выше?
3. Вычислите интегралы:
а)  ; б)
; б)  ; в)
; в) 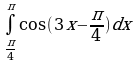 .
.
4. Вычислите площадь фигуры, ограниченной линиями:
а) y= x2 –2x+4, y=3, x=–1;
б) y=sinx, y=1/2, x=p/6, x=5p/6.
Блок 2 Контрольный тест Вариант 2
1. Найдите неопределённый интеграл:
а)  ; б)
; б) ; в)
; в)  ; г)
; г)  ;
;
д) 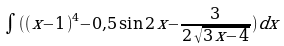 .
.
2. Графики первообразных F1 и F2 функции f(x)=–6x2 +4x+1 проходят через точки М(0;2) и N(1;3). Какова разность этих двух первообразных? Какой из графиков F1 и F2 расположен выше?
3. Вычислите интегралы:
а)  ; б)
; б)  ; в)
; в) 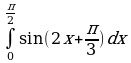 .
.
4. Вычислите площадь фигуры, ограниченной линиями:
а) y= x3 , y=8, x=1;
б) y=cosx, y=1, x=–p/3, x=p/3.
Блок 3 Задачи.
Покажите, что функции F1 (x)=tg2x, F2 (x)=  , F3 (x)=
, F3 (x)= 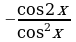 являются первообразными функции f(x)=
являются первообразными функции f(x)= 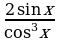 на интервале (-p/2; p/2). Найдите первообразную для функции f на интервале
на интервале (-p/2; p/2). Найдите первообразную для функции f на интервале
(-p/2; p/2), график которой проходит через точку (0;10).
2. Найдите уравнение кривой, проходящей через точку (2;3), если угловой коэффициент касательной в точке x равен 3x2 .
3. Материальная точка движется по координатной прямой со скоростью v(t)= sint cost. Найдите уравнение движения точки, если при t=p/4 её координата равна 3.
4. Найдите площадь фигуры, ограниченной параболой 2x–4x2 , линией x=–2 и касательной к данной параболе, проведённой через её точку с абсциссой x=0.
5. В каком отношении делится площадь квадрата параболой, проходящей через две его соседние вершины и касающейся одной стороной в её середине?
Блок 3 Тест самоконтроля
1.Приведите пример функции f и её первообразной F, заданных на R таких, что F(x)=f(p/2–x).
Ответ: f(x)=cosx, F(x)=sinx.
2. Являются ли первообразными для одной и той же функции F1(x)=2соs2x, F2(x)=cos2x, F3(x)=3соs2x+ sin2x ? Если да, то укажите эту функцию.
Ответ: f(x)=–2sinx, F2(x)= F1(x)–1, F3(x)= F1(x)+1.
3. Найдите уравнение кривой, проходящей через точку (3;7), если угловой коэффициент касательной в точке x равен x2 .
Ответ: y=1/3x3–2 (угловой коэффициент касательной в точке x – производная в этой точке).
4. Материальная точка движется по координатной прямой со скоростью v(t)= 2соs  . Найдите уравнение движения точки, если при t=p/3 её координата равна 4.
. Найдите уравнение движения точки, если при t=p/3 её координата равна 4.
Ответ: x(t)= 4sin  +2 ( x’(t)= v(t) ).
+2 ( x’(t)= v(t) ).
5. Найдите площадь фигуры, ограниченной параболой y=2,5+2x–0,5x2 , линией x=–1 и касательной к данной параболе, проведённой через её точку с абсциссой x=3.
Ответ: 10
Блок 3 Контрольный тест Вариант 1
1.Приведите пример ограниченной на интервале функции с неограниченной на этом интервале первообразной.
2.Приведите пример функции f и её первообразной F, заданных на R таких, что f(x)=2F(p/2–2x).
3. Найдите уравнение кривой, проходящей через точку (p/4 ;5 ), если угловой коэффициент касательной в точке x равен 6cosx .
), если угловой коэффициент касательной в точке x равен 6cosx .
4.Точка движется по координатной прямой с ускорением а(t)=–2t. В начальный момент t0 =1 её координата x0 =4 и скорость v0 =2. Найдите уравнение движения точки.
5. Найдите площадь фигуры, ограниченной параболой x2– 4x+5 и касательными к ней, проведёнными через её точки с абсциссами x=1 и x=3.
Блок 3 Контрольный тест Вариант 2
1.Приведите пример ограниченной на R функции с ограниченной на R первообразной.
2.Приведите пример функции f и её первообразной F, заданных на R таких, что F(x)=–f(p/2–x).
3. Найдите уравнение кривой, проходящей через точку (p/4 ;–3 ), если угловой коэффициент касательной в точке x равен sinx .
), если угловой коэффициент касательной в точке x равен sinx .
4.Точка движется по координатной прямой с ускорением а(t)=sint. В начальный момент t0 =p/2 её координата x0 =2 и скорость v0 =1. Найдите уравнение движения точки.
5. Найдите площадь фигуры, ограниченной параболой y=8x–2x2 , линией x=0 и касательной к данной параболе, проведённой через её вершину.
Блок 4
1. Докажите следующую формулу:  , где u, v –произвольные функции, dv, du – производные функций v и u.соответственно.
, где u, v –произвольные функции, dv, du – производные функций v и u.соответственно.
2. Используя выше доказанную формулу найти интеграл 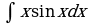
3.Найдите наибольшее и наименьшее значение интеграла 
Уровневая контрольная работа
1. Найдите неопределённый интеграл
а)  ;
;
б) 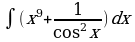 ;
;
2. Вычислите площадь фигуры ограниченной графиками функций
 и
и 
3. Вычислите определённый интеграл
а) 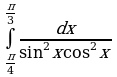 ;
;
б) 
4. Найдите площадь фигуры ограниченной графиком функции 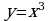 , касательной к нему в точке х=1 и осью у.
, касательной к нему в точке х=1 и осью у.
5. При каком отрицательном значении параметра а площадь фигуры, ограниченной линиями  равна
равна 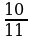 .
.
При составлении тестов использовались задания учебников [2, 5, 9, 11, 14].







 ,
, , (-
, (- ; +
; +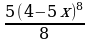 ;
; ;
;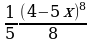 ;
; ;
; ,следовательно у= –х4 имеет первообразную у= –
,следовательно у= –х4 имеет первообразную у= – . Решение воспользуемся правилом нахождения первообразных №3 (если функция y=g(x) имеет первообразную y=G(x) ,то функция y=g(tx+m) имеет первообразную y=
. Решение воспользуемся правилом нахождения первообразных №3 (если функция y=g(x) имеет первообразную y=G(x) ,то функция y=g(tx+m) имеет первообразную y=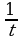 G(tx+m)), т.е. t= –15, m=4 , а g(x)=
G(tx+m)), т.е. t= –15, m=4 , а g(x)= , следовательно
, следовательно  . Ответ: F(x)=
. Ответ: F(x)= 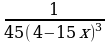 +С.
+С. . Ответ: F(x)= –2tg(π/3–x);
. Ответ: F(x)= –2tg(π/3–x); 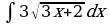 Решение: воспользуемся правилами нахождения неопределённого интеграла:
Решение: воспользуемся правилами нахождения неопределённого интеграла:  .
.
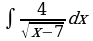 . Ответ: 8
. Ответ: 8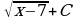 ; в)
; в) 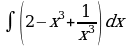 . Ответ: 2х –0,25х4 –0,5х –2+С;
. Ответ: 2х –0,25х4 –0,5х –2+С; ; Ответ: –0,25(3+8х)–2 –0,5sin2x; д)
; Ответ: –0,25(3+8х)–2 –0,5sin2x; д)  . Ответ: 0,5х2 –sinx –4x –4;
. Ответ: 0,5х2 –sinx –4x –4; . Решение: воспользуемся формулой Ньютона–Лейбница
. Решение: воспользуемся формулой Ньютона–Лейбница  .
. 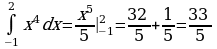 . Ответ:
. Ответ:  б)
б)  . Ответ: 1; в)
. Ответ: 1; в)  . Ответ: 20;
. Ответ: 20; , y=0, x=–1, x=1. Фигура ограниченная данными линиями является криволинейной трапецией и её площадь равна:
, y=0, x=–1, x=1. Фигура ограниченная данными линиями является криволинейной трапецией и её площадь равна:  Ответ: 0,4.
Ответ: 0,4.  , xÎ(-
, xÎ(-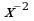 , f(x)=
, f(x)= 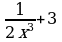 , xÎ(0;
, xÎ(0;  ; б)
; б)  ; в)
; в) 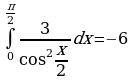 ; г)
; г)  ; д)
; д)  ?
? ; б)
; б)  ; в)
; в) 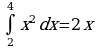 ;
;  д)
д)  ;
; ?
? , где
, где  и
и 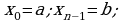

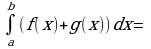
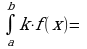
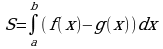



 ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
; 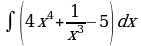 ; е)
; е)  .
. 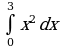 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;  ; е)
; е)  .
.  ; б)
; б) 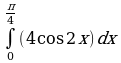 ; в)
; в)  ; г)
; г)  ;
;  . Решение: заметим, что подынтегральная функция не является функцией из таблицы в явном виде, поэтому её необходимо преобразовать:
. Решение: заметим, что подынтегральная функция не является функцией из таблицы в явном виде, поэтому её необходимо преобразовать: 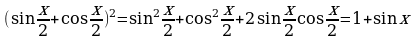 , интеграл от полученной функции легко вычисляется:
, интеграл от полученной функции легко вычисляется:  . Ответ:
. Ответ:  +С.
+С. 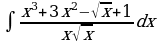 . Решение: аналогично примеру под буквой а) упрощаем подынтегральную функцию и вычисляем интеграл:
. Решение: аналогично примеру под буквой а) упрощаем подынтегральную функцию и вычисляем интеграл:  .
. 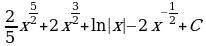 .
.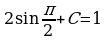 , откуда С= –1. Ответ: F(x)=2sinx –1.
, откуда С= –1. Ответ: F(x)=2sinx –1. ; Решение: упрощаем подынтегральную функцию и вычисляем определённый интеграл:
; Решение: упрощаем подынтегральную функцию и вычисляем определённый интеграл:  . Ответ:
. Ответ: 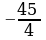 .
.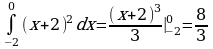 .
.  .
. , f(x)= 2 –
, f(x)= 2 –  sin
sin , f(x)= –
, f(x)= –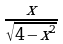 , xÎ(-2;2);
, xÎ(-2;2);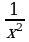 , f(x)=
, f(x)= 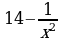 , xÎ(0;
, xÎ(0; 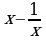 , f(x)=
, f(x)= 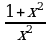 , xÎ(0;
, xÎ(0;  найдите первообразную, график которой
найдите первообразную, график которой +3; б) F(х)=2
+3; б) F(х)=2 ; б)
; б) ; в)
; в) ;
; ; д)
; д) ?
? ; б)
; б) ; в)
; в) 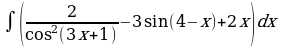 ; г)
; г)  ;
;  .
. ; б)
; б)  ; в)
; в) 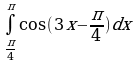 .
. ; б)
; б) ; в)
; в)  ; г)
; г)  ;
; 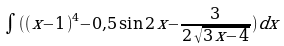 .
. ; б)
; б)  ; в)
; в) 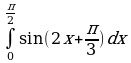 .
. , F3 (x)=
, F3 (x)= 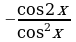 являются первообразными функции f(x)=
являются первообразными функции f(x)= 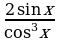 на интервале (-p/2; p/2). Найдите первообразную для функции f на интервале
на интервале (-p/2; p/2). Найдите первообразную для функции f на интервале  . Найдите уравнение движения точки, если при t=p/3 её координата равна 4.
. Найдите уравнение движения точки, если при t=p/3 её координата равна 4.
 ), если угловой коэффициент касательной в точке x равен 6cosx .
), если угловой коэффициент касательной в точке x равен 6cosx . , где u, v –произвольные функции, dv, du – производные функций v и u.соответственно.
, где u, v –произвольные функции, dv, du – производные функций v и u.соответственно.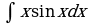

 ;
;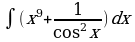 ;
; и
и 
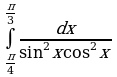 ;
;
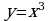 , касательной к нему в точке х=1 и осью у.
, касательной к нему в точке х=1 и осью у. равна
равна 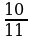 .
.
















