Теорема Эйлера.

Теорема Эйлера

Выполнила: Трубецкая Кристина

Проверила: Дубинская И.А.

Эйлерова характеристика

• X= В – Р + Г

Обозначение:

X – эйлерова характеристика

В – кол-во вершины многогранника

Р – кол-во ребер многогранника

Г – кол-во граней многогранника

Формулировка теоремы

• Для любого выпуклого многогранника эйлерова характеристика равна 2

• В – Р + Г = 2

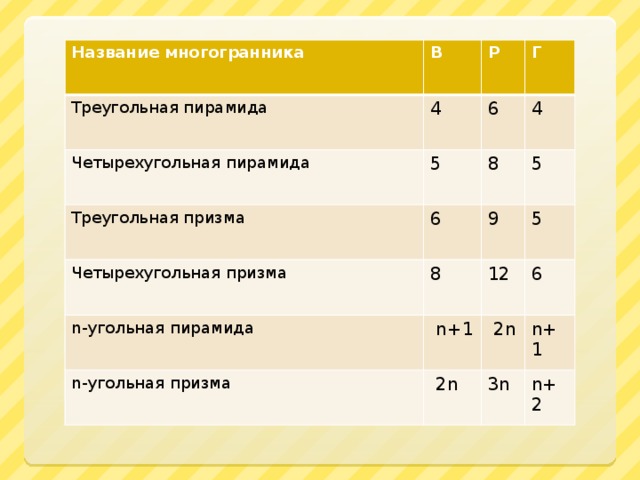
Название многогранника

В

Треугольная пирамида

Р

4

Четырехугольная пирамида

Г

6

5

Треугольная призма

6

Четырехугольная призма

4

8

n-угольная пирамида

8

5

9

5

12

n+1

n-угольная призма

6

2n

2n

3n

n+1

n+2

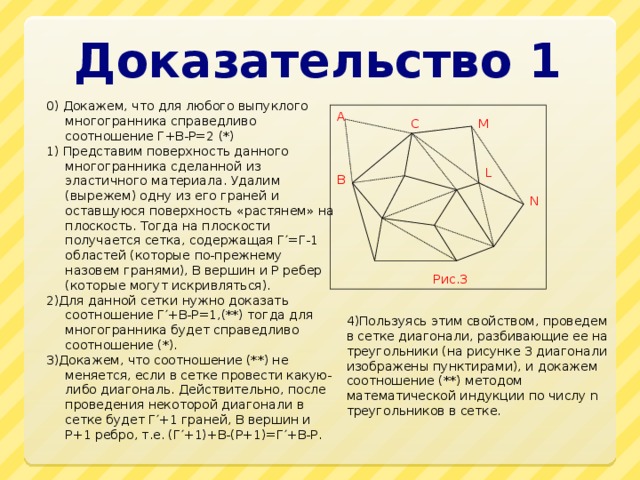
Доказательство 1

0) Докажем, что для любого выпуклого многогранника справедливо соотношение Г+В-Р=2 (*)

1) Представим поверхность данного многогранника сделанной из эластичного материала. Удалим (вырежем) одну из его граней и оставшуюся поверхность «растянем» на плоскость. Тогда на плоскости получается сетка, содержащая Г′=Г-1 областей (которые по-прежнему назовем гранями), В вершин и Р ребер (которые могут искривляться).

2)Для данной сетки нужно доказать соотношение Г′+В-Р=1,(**) тогда для многогранника будет справедливо соотношение (*).

3)Докажем, что соотношение (**) не меняется, если в сетке провести какую-либо диагональ. Действительно, после проведения некоторой диагонали в сетке будет Г′+1 граней, В вершин и Р+1 ребро, т.е. (Г′+1)+В-(Р+1)=Г′+В-Р.

A

C

M

L

B

N

Рис.3

4)Пользуясь этим свойством, проведем в сетке диагонали, разбивающие ее на треугольники (на рисунке 3 диагонали изображены пунктирами), и докажем соотношение (**) методом математической индукции по числу n треугольников в сетке.

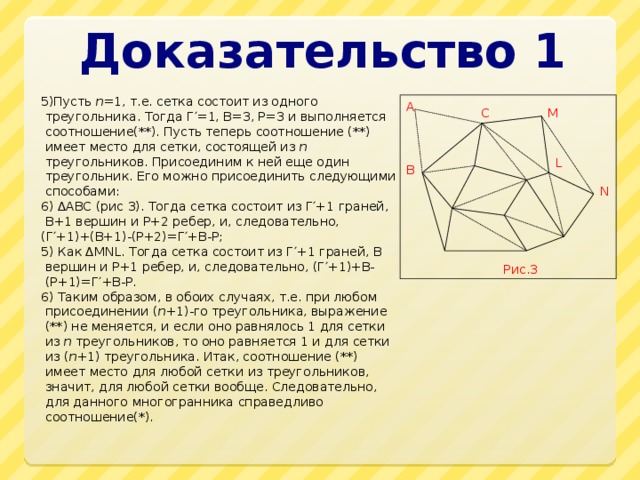
Доказательство 1

5)Пусть n =1, т.е. сетка состоит из одного треугольника. Тогда Г′=1, В=3, Р=3 и выполняется соотношение(**). Пусть теперь соотношение (**) имеет место для сетки, состоящей из n треугольников. Присоединим к ней еще один треугольник. Его можно присоединить следующими способами:

6) ∆ABC (рис 3). Тогда сетка состоит из Г′+1 граней, В+1 вершин и Р+2 ребер, и, следовательно,

(Г′+1)+(В+1)-(Р+2)=Г′+В-Р;

5) Как ∆MNL. Тогда сетка состоит из Г′+1 граней, В вершин и Р+1 ребер, и, следовательно, (Г′+1)+В-(Р+1)=Г′+В-Р.

6) Таким образом, в обоих случаях, т.е. при любом присоединении ( n +1)-го треугольника, выражение (**) не меняется, и если оно равнялось 1 для сетки из n треугольников, то оно равняется 1 и для сетки из ( n +1) треугольника. Итак, соотношение (**) имеет место для любой сетки из треугольников, значит, для любой сетки вообще. Следовательно, для данного многогранника справедливо соотношение(*).

A

C

M

L

B

N

Рис.3

Доказательство 2

• 1)Возьмем с наружи многогранника точку О вблизи от какой-либо грани F и спроектируем остальные грани на F из центра О (рис. 9). Их проекции образуют разбиение грани F на многоугольники.
• Подсчитаем двумя способами сумму α углов всех полученных многоугольников и самой грани F.
• Сумма углов n-угольника равна ∏(n - 2).
• Сложим эти числа для всех граней (включая грань F). Сумма членов вида ∏n равна общему числу сторон всех граней, т.е. 2Р - ведь каждое из Р рёбер принадлежит двум граням. А так как у нас всего Г слагаемых, α = ∏(2Р - 2Г).
• Теперь найдем сумму углов при каждой вершине разбиения и сложим эти суммы. Если вершина лежит внутри грани F, то сумма углов вокруг нее равна 2∏. Таких вершин В-k, где k- число вершин самой грани F, а значит, их вклад в равен 2∏(В - k). Углы при вершинах F считаются в сумме дважды (как углы F и как углы многоугольников разбиения); их вклад равен 2∏(k - 2). Таким образом,

α = 2∏(B - k) + 2∏(k - 2) = 2∏(B - 2). Приравнивая два результата и сокращения на 2π, получаем требуемое равенство Р - Г = В - 2.

Следствия

• Р + 6≤ 3В и Р + 6≤ 3Г;

• Г + 4≤ 2В и В + 4≤ 2Г;

• У всякого многогранника есть хотя бы одна треугольная, четырехугольная или пятиугольная грань, а также хотя бы один трехгранный, четырехгранный или пятигранный пространственный угол;

• Сумма плоских углов всех граней многогранника равна 2∏ В- 4∏.