В.1.
1. Найдите значение выражения 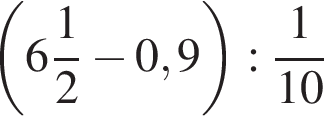 .
.
2. Найдите значение выражения 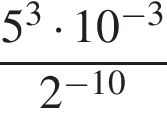 .
.
3. Налог на доходы составляет 13 % от заработной платы. После удержания налога на доходы Мария Константиновна получила 17 400 рублей. Сколько рублей составляет заработная плата Марии Константиновны?
4. Площадь четырёхугольника можно вычислить по формуле 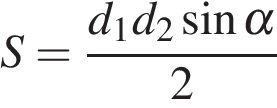 , где
, где 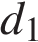 и
и 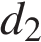 — длины диагоналей четырёхугольника,
— длины диагоналей четырёхугольника,  — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали
— угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали 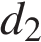 , если
, если 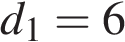 ,
, 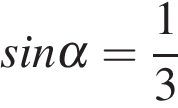 , а
, а 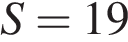 .
.
5. Найдите значение выражения 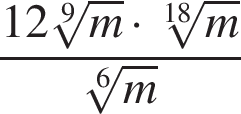 при
при  .
.
6. Для ремонта квартиры требуется 63 рулона обоев. Сколько пачек обойного клея нужно купить, если одна пачка клея рассчитана на 6 рулонов?
7. Найдите корень уравнения 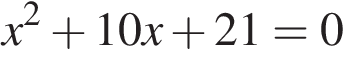 . Если уравнение имеет более одного корня, в ответе укажите меньший из них.
. Если уравнение имеет более одного корня, в ответе укажите меньший из них.
8. 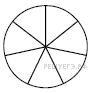 На рисунке показано, как выглядит колесо с 7 спицами. Сколько будет спиц в колесе, если угол между соседними спицами в нём будет равен 18°?
На рисунке показано, как выглядит колесо с 7 спицами. Сколько будет спиц в колесе, если угол между соседними спицами в нём будет равен 18°?
9. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | | ВОЗМОЖНЫЕ ЗНАЧЕНИЯ |
| А) результат при прыжке в высоту Б) высота полёта самолёта В) толщина рыболовной сетки Г) длина стены в комнате | | 1) 520 см 2) 8 км 3) 1,8 м 4) 0,3 мм |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
10. Помещение освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,15. Найдите вероятность того, что в течение года обе лампы перегорят.
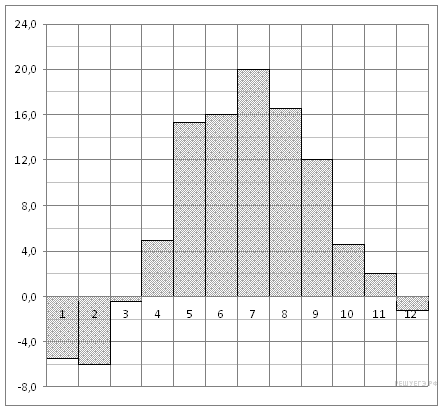
11. На диаграмме показана среднемесячная температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев, когда среднемесячная температура была отрицательной.
12. В магазине одежды объявлена акция: если покупатель приобретает товар на сумму свыше 10 000 руб., он получает сертификат на 1000 рублей, который можно обменять в том же магазине на любой товар ценой не выше 1000 руб. Если покупатель участвует в акции, он теряет право возвратить товар в магазин.
Покупатель И. хочет приобрести куртку ценой 9500 руб., футболку ценой 800 руб. и носки ценой 900 руб. В каком случае И. заплатит за покупку меньше всего:
1) И. купит все три товара сразу.
2) И. купит сначала куртку и футболку, носки получит за сертификат.
3) И. купит сначала куртку и носки, получит футболку за сертификат.
В ответ запишите, сколько рублей заплатит И. за покупку в этом случае.
13. 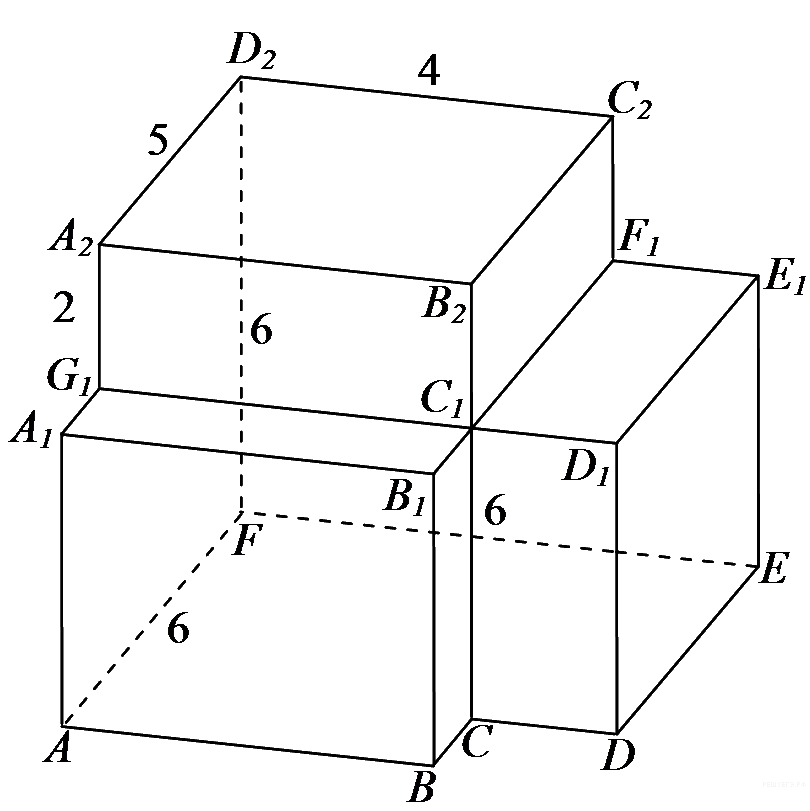 Найдите угол АД2Е многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
Найдите угол АД2Е многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
14. На рисунке изображён график функции, к которому проведены касательные в четырёх точках.
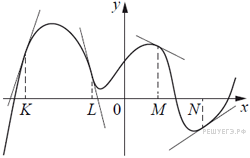
Ниже указаны значения производной в данных точках. Пользуясь графиком, поставьте в соответствие каждой точке значение производной в ней.
| ТОЧКИ | | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
| А) K Б) L В) M Г) N | | 1) −4 2) 3 3)  4) −0,5 |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
15. 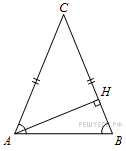 В треугольнике АВС
В треугольнике АВС  , высота
, высота  равна 4,
равна 4, 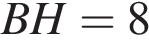 . Найдите tgВАС..
. Найдите tgВАС..
16. 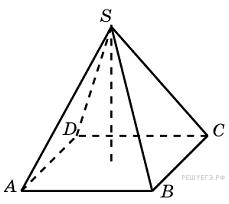 В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.
В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.
17. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | | РЕШЕНИЯ |
| А) 0,5x ≥ 2 Б) 0,5x ≤ 2 В) 2x ≤ 2 Г) 2x ≥ 2 | | 1) x ≥ −1 2) x ≥ 1 3) x ≤ −1 4) x ≤ 1 |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
18. Некоторые сотрудники фирмы летом 2014 года отдыхали в Крыму, а некоторые ― в Сочи. Все сотрудники, которые отдыхали в Сочи, не отдыхали в Крыму. Выберите утверждения, которые верны при указанных условиях.
1) Если сотрудник этой фирмы летом 2014 года отдыхал в Крыму, то он отдыхал и в Сочи.
2) Каждый сотрудник этой фирмы отдыхал летом 2014 года в Крыму.
3) Среди сотрудников этой фирмы, которые не отдыхали в Сочи летом 2014 года, есть хотя бы один, который отдыхал в Крыму.
4) Нет ни одного сотрудника этой фирмы, который летом 2014 года отдыхал и в Крыму, и в Сочи.
В бланк ответов запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
19. Вычеркните в числе 53164018 три цифры так, чтобы получившееся число делилось на 15. В ответе укажите ровно одно получившееся число.
20. Саша пригласил Петю в гости, сказав, что живёт в восьмом подъезде в квартире № 468, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом двенадцатиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
В.2.
1. Найдите значение выражения 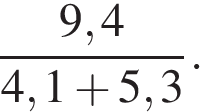
2. Найдите значение выражения 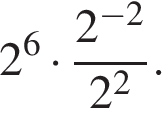
3. Студент получил свой первый гонорар в размере 900 рублей за выполненный перевод. Он решил на все полученные деньги купить букет лилий для своей учительницы английского языка. Какое наибольшее количество лилий сможет купить студент, если удержанный у него налог на доходы составляет 13% гонорара, лилии стоят 120 рублей за штуку и букет должен состоять из нечетного числа цветов?
4. Теорему косинусов можно записать в виде где 
 и
и  — стороны треугольника, а
— стороны треугольника, а  — угол между сторонами
— угол между сторонами  и bПользуясь этой формулой, найдите величину если и c=11.
и bПользуясь этой формулой, найдите величину если и c=11.
5. Найдите значение выражения
6. Сырок стоит 17 рублей 60 копеек. Какое наибольшее число сырков можно купить на 130 рублей?
7. Найдите корень уравнения .
8. Два садовода, имеющие прямоугольные участки размерами 35 м на 40 м с общей границей, договорились и сделали общий прямоугольный пруд размером 20 м на 14 м (см. чертёж), причём граница участков проходит точно через центр. Какова площадь (в квадратных метрах) оставшейся части участка каждого садовода?
9. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | | ВОЗМОЖНЫЕ ЗНАЧЕНИЯ |
| А) масса взрослого человека Б) масса грузового автомобиля В) масса книги Г) масса пуговицы | | 1) 8 т 2) 5 г 3) 65 кг 4) 300 г |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
10. В кармане у Миши было четыре конфеты — «Грильяж», «Белочка», «Коровка» и «Ласточка», а также ключи от квартиры. Вынимая ключи, Миша случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Грильяж».
11. На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат — температура двигателя в градусах Цельсия. Определите по графику, сколько минут двигатель нагревался от температуры 60 °C до температуры 90 °C.
12. В таблице указаны доходы и расходы фирмы за 5 месяцев.
| Месяц | Доход, тыс. руб. | Расход, тыс. руб. |
| Июль | 115 | 110 |
| Август | 125 | 130 |
| Сентябрь | 140 | 120 |
| Октябрь | 120 | 110 |
| Ноябрь | 130 | 90 |
Пользуясь таблицей, поставьте в соответствие каждому из указанных периодов времени характеристику доходов и расходов.
| ПЕРИОДЫ
ВРЕМЕНИ | | ХАРАКТЕРИСТИКИ |
| А) август Б) сентябрь В) октябрь Г) ноябрь | | 1) расход в этом месяце больше, чем расход в предыдущем 2) доход в этом месяце меньше, чем доход в предыдущем 3) наибольший доход в период с августа по ноябрь 4) наибольшая разница между доходом и расходом |
13. Цилиндр описан около шара. Объем шара равен 38. Найдите объем цилиндра.
14. На рисунке показано изменение температуры воздуха на протяжении суток. По горизонтали указывается время суток, по вертикали — значение температуры в градусах Цельсия.
Пользуясь диаграммой, установите связь между промежутками времени и характером изменения температуры.
| ПРОМЕЖУТКИ ВРЕМЕНИ | | ХАРАКТЕР ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ |
| А) 00:00−06:00 Б) 06:00−12:00 В) 15:00−18:00 Г) 18:00−00:00 | | 1) Температура снижалась быстрее всего 2) Температура сначала уменьшалась, а затем возрастала 3) Температура росла быстрее всего 4) Температура росла медленнее всего |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
15. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
16. Найдите объем правильной четырехугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно  .
.
17. Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого столбца. Установите соответствие между неравенствами и множествами их решениями.
| НЕРАВЕНСТВА | | РЕШЕНИЯ |
| А) Б) В) Г) | | |
Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
18. В зоомагазине в один из аквариумов запустили 20 рыбок. Длина каждой рыбки больше 3 см, но не превышает 13 см. Выберите утверждения, которые следуют из данной информации.
1) Десять рыбок в этом аквариуме меньше 8 см.
2) В этом аквариуме нет рыбки длиной 14 см.
3) Разница в длине любых двух рыбок не больше 10 см.
4) Длина каждой рыбки больше 10 см.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
19. Сумма цифр трёхзначного натурального числа А делится на 12. Сумма цифр числа (А + 6) также делится на 12. Найдите наименьшее число А, удовлетворяющее условию А 700.
20. Во всех подъездах дома одинаковое число этажей, а на каждом этаже одинаковое число квартир. При этом число этажей в доме больше числа квартир на этаже, число квартир на этаже больше числа подъездов, а число подъездов больше одного. Сколько этажей в доме, если всего в нём 110 квартир?
В.3.
1. Найдите значение выражения 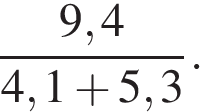
2. Найдите значение выражения .
3. Налог на доходы составляет 13% от заработной платы. После удержания налога на доходы Мария Константиновна получила 6960 рублей. Сколько рублей составляет заработная плата Марии Константиновны?
4. Найдите  из равенства если
из равенства если  и
и
5. Найдите значение выражения при .
6. В пачке 500 листов бумаги формата А4. За неделю в офисе расходуется 600 листов. Какого наименьшего количества пачек бумаги хватит на 6 недель?
7. Найдите корень уравнения .
8. Пожарную лестницу длиной 13 м приставили к окну дома (см. рисунок). Нижний конец лестницы отстоит от стены дома на 5 м. На какой высоте расположено окно? Ответ дайте в метрах.
9. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | | ВОЗМОЖНЫЕ ЗНАЧЕНИЯ |
| А) объём воды в Азовском море Б) объём ящика с инструментами В) объём грузового отсека транспортного самолёта Г) объём бутылки растительного масла | | 1) 150 м3 2) 1 л 3) 76 л 4) 256 км3 |
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
10. На экзамене 40 вопросов. Дима не выучил 6 из них. Найдите вероятность того, что ему попадется выученный вопрос.
11. В соревнованиях по метанию молота участники показали следующие результаты:
| Спортсмен | Результат попытки, м |
| I | II | III | IV | V | VI |
| Донников | 49 | 50,5 | 50 | 51 | 51 | 49,5 |
| Мелихов | 51 | 52,5 | 49,5 | 50 | 52 | 51,5 |
| Иванов | 50,5 | 50 | 49 | 51,5 | 51 | 51,5 |
| Теплицын | 52 | 51 | 52 | 50,5 | 51,5 | 51 |
Места распределяются по результатам лучшей попытки каждого спортсмена: чем дальше он метнул молот, тем лучше. Каков результат лучшей попытки (в метрах) спортсмена, занявшего второе место?
12. На игре КВН судьи поставили следующие оценки командам за конкурсы:
| Команда | Баллы за конкурс
«Приветствие» | Баллы за конкурс
«СТЭМ» | Баллы за музыкальный
конкурс |
| «АТОМ» | 30 | 21 | 26 |
| «Шумы» | 27 | 24 | 24 |
| «Топчан» | 28 | 23 | 25 |
| «Лёлек и Болек» | 30 | 22 | 27 |
Для каждой команды баллы по всем конкурсам суммируются, победителем считается команда, набравшая в сумме наибольшее количество баллов. Сколько в сумме баллов у команды-победителя?
13. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?
14. На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На горизонтальной оси отмечено число оборотов в минуту, на вертикальной оси — крутящий момент в Н · м.
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику крутящего момента.
| ИНТЕРВАЛЫ ВРЕМЕНИ | | ХАРАКТЕРИСТИКИ |
| А) 0 − 1000 об./мин Б) 1500 − 2000 об./мин В) 3000 − 4000 об./мин Г) 4000 − 6000 об./мин | | 1) Крутящий момент рос быстрее всего. 2) Крутящий момент падал. 3) Крутящий момент не менялся. 4) Крутящий момент не превышал 20 H · м на всем интервале.. |
В таблице под каждой буквой укажите соответствующий номер.
15. В параллелограмме . . Найдите высоту, опущенную на сторону  .
.
16. Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 7 и 9, а второго — 2 и 9. Во сколько раз площадь боковой поверхности первого конуса больше площади боковой поверхности второго?
17. На координатной прямой отмечены числа  и
и  .
.

Расположите числа в порядке убывания:
18. Баскетбольная команда на площадке состоит из пяти игроков. Средний рост игроков составляет 195 см, при этом рост наиболее высокого игрока равен 205 см, а наиболее низкого — 190 см. Выберите утверждения, которые непосредственно следуют из приведённых данных.
1) По крайней мере два игрока команды имеют рост менее 195 см
2) Средний рост трёх остальных игроков меньше 195 см
3) Каждый из трёх остальных игроков ниже 195 см
4) Рост второго по высоте игрока больше 195 см
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
19. Сумма цифр трёхзначного числа A делится на 13. Сумма цифр числа A+5 также делится на 13. Найдите такое число A.
20. В корзине лежат 25 грибов: рыжики и грузди. Известно, что среди любых 11 грибов имеется хотя бы один рыжик, а среди любых 16 грибов хотя бы один груздь. Сколько рыжиков в корзине?
В.4.
1. Найдите значение выражения .
2. Найдите значение выражения .
3. Футболка стоила 500 рублей. После снижения цены она стала стоить 390 рублей. На сколько процентов была снижена цена на футболку?
4. Мощность постоянного тока (в ваттах) вычисляется по формуле где  — сила тока (в амперах),
— сила тока (в амперах),  — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление
— сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление  (в омах), если мощность составляет 144,5 Вт, а сила тока равна 8,5 А.
(в омах), если мощность составляет 144,5 Вт, а сила тока равна 8,5 А.
5. Найдите значение выражения .
6. В летнем лагере 150 детей и 21 воспитатель. В одном автобусе можно перевозить не более 20 пассажиров. Какое наименьшее количество таких автобусов понадобится, чтобы за один раз перевезти всех из лагеря в город?
7. Найдите корень уравнения
8. Рыболовное хозяйство строит бассейн для разведения рыбы. Бассейн имеет форму прямоугольника со сторонами 4 м и 12 м. В центре бассейна находится техническая постройка, которая имеет форму прямоугольника со сторонами 2 м и 3 м. Найдите площадь оставшейся части бассейна.
9. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | | ВОЗМОЖНЫЕ ЗНАЧЕНИЯ |
| А) площадь классной доски Б) площадь озера Байкал В) площадь листа А4 Г) площадь Евразии | | 1) 32 тыс. км2 2) 55 млн км2 3) 600 см2 4) 4 м2 |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
10. На олимпиаде в вузе участников рассаживают по трём аудиториям. В первых двух по 120 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчёте выяснилось, что всего было 250 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
11. На диаграмме приведены данные о протяжённости восьми крупнейших рек России. Первое место по протяжённости занимает Лена. На каком месте по протяжённости находится Амур?
12. Клиент хочет арендовать автомобиль на сутки для поездки протяжённостью 700 км. В таблице приведены характеристики трёх автомобилей и стоимость их аренды.
| Автомобиль | Топливо | Расход топлива
(л на 100 км) | Арендная плата
(руб. за 1 сутки) |
| А | Дизельное | 5 | 4200 |
| Б | Бензин | 11 | 2700 |
| В | Газ | 16 | 3000 |
Помимо аренды, клиент обязан оплатить топливо для автомобиля на всю поездку. Цена дизельного топлива — 30 рублей за литр, бензина — 35 рублей за литр, газа — 20 рублей за литр. Сколько рублей заплатит клиент за аренду и топливо, если выберет самый дешёвый вариант?
13. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
14. На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
| ПЕРИОДЫ ВРЕМЕНИ | | ХАРАКТЕРИСТИКИ |
| А) A Б) B В) C Г) D | | 1) 1,4 2) −0,7 3) 0,5 4) −1,8 |
В таблице под каждой буквой укажите соответствующий номер.
15.
Найдите площадь прямоугольного треугольника, если его катеты равны 9 и 18.
16. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности.
17. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | | РЕШЕНИЯ |
| А) Б) В) Г) | | |
В таблице под каждой буквой укажите соответствующий номер.
18. На зимней Олимпиаде сборная Канады завоевала медалей больше, чем сборная Нидерландов, сборная Белоруссии — меньше, чем сборная Нидерландов, а сборная Швейцарии — меньше, чем сборная Канады. Выберите утверждения, которые верны при указанных условиях.
1) Сборная Канады завоевала больше медалей, чем каждая из остальных трёх сборных.
2) Сборная Белоруссии завоевала меньше медалей, чем сборная Канады.
3) Среди названных сборных есть три, завоевавшие равное количество медалей.
4) Из названных сборных команда Белоруссии заняла второе место по числу медалей.
19. Найдите трёхзначное число A, обладающее всеми следующими свойствами:
· сумма цифр числа A делится на 4;
· сумма цифр числа (A + 2) делится на 4;
· число A больше 200 и меньше 400.
В ответе укажите какое-нибудь одно такое число.
20. Врач прописал пациенту принимать лекарство по такой схеме: в первый день он должен принять 20 капель, а в каждый следующий день — на 3 капли больше, чем в предыдущий. После 15 дней приёма пациент делает перерыв в 3 дня и продолжает принимать лекарство по обратной схеме: в 19-й день он принимает столько же капель, сколько и в 15-й день, а затем ежедневно уменьшает дозу на 3 капли, пока дозировка не станет меньше 3 капель в день. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 200 капель?
ОТВЕТЫ
| В1 | 1 | 56 | | 2 | 128 | | 3 | 20000 | | 4 | 19 | | 5 | 12 | | 6 | 11 | | 7 | -7 | | 8 | 20 | | 9 | 3241 | | 10 | 0,0225 | | 11 | 4 | | 12 | 10300 | | 13 | 60 | | 14 | 2143 | | 15 | 0,5 | | 16 | 13 | | 17 | 3142 | | 18 | 34 | | 19 | 53160 | | 20 | 10 |
| В2
| 1 | 1 | | 2 | 4 | | 3 | 5 | | 4 | 0,2 | | 5 | 0,75 | | 6 | 7 | | 7 | 3 | | 8 | 1260 | | 9 | 3142 | | 10 | 0,25 | | 11 | 3 | | 12 | 1324 | | 13 | 57 | | 14 | 4312 | | 15 | 2 | | 16 | 16 | | 17 | 3124 | | 18 | 23 | | 19 | 798 | | 20 | 11 |
| В3
| 1 | 1 | | 2 | 5 | | 3 | 8000 | | 4 | 85 | | 5 | 0,4 | | 6 | 8 | | 7 | -0,5 | | 8 | 12 | | 9 | 4312 | | 10 | 0,85 | | 11 | 52 | | 12 | 79 | | 13 | 3 | | 14 | 4132 | | 15 | 9 | | 16 | 3,5 | | 17 | 4321 | | 18 | 12 | | 19 | 899 | | 20 | 15 |
| В4
| 1 | 10 | | 2 | 900 | | 3 | 22 | | 4 | 2 | | 5 | 42 | | 6 | 9 | | 7 | -2 | | 8 | 42 | | 9 | 4132 | | 10 | 0,04 | | 11 | 7 | | 12 | 5240 | | 13 | 104 | | 14 | 4132 | | 15 | 81 | | 16 | 22 | | 17 | 1243 | | 18 | 12 | | 19 | 299 | | 20 | 7 |
|







 На рисунке показано, как выглядит колесо с 7 спицами. Сколько будет спиц в колесе, если угол между соседними спицами в нём будет равен 18°?
На рисунке показано, как выглядит колесо с 7 спицами. Сколько будет спиц в колесе, если угол между соседними спицами в нём будет равен 18°?
 Найдите угол АД2Е многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
Найдите угол АД2Е многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
 В треугольнике АВС
В треугольнике АВС  В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.
В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды. 









