МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«САРАТОВСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ
Н.Г. ЧЕРНЫШЕВСКОГО»
Кафедра основ математики и информатики на базе
МАОУ «Лицей математики и информатики» г. Саратова
ОТЧЕТ ПО ОЗНАКОМИТЕЛЬНОЙ ПРАКТИКЕ
студента 1 курса 121 группы
направление 44.03.01 Педагогическое образование (профиль – математическое образование) механико-математического факультета
Фроловой Юлии Александровны
| Место прохождения практики: | по месту жительства |
| Сроки прохождения практики: | 09.03.2021 – 22.03.2021 |
| Оценка |
|
Руководитель практики
| ассистент |
|
|
| А.А. Вдовиченко |
|
|
| подпись, дата |
|
|
Саратов 2021
СОДЕРЖАНИЕ
Введение…………………………………………………………………. 3
Задание 1. Работа с первоисточником………………………………… 4
Задание 2. Структурирование материала …………………………….. 5
Задание 3. Методическая разработка по теме ……………………….. 13
Заключение ………………………………………………………………18
Список использованных источников…………………………………..19
ВВЕДЕНИЕ
Учебная ознакомительная практика проходила в сроки с 09.03.2021 по 22.03.2021.
Цель практики– обеспечение готовности к профессиональной деятельности, формирование общепрофессиональных и профессиональных компетенций:
ОПК-8 – способность осуществлять педагогическую деятельность на основе специальных научных знаний;
ПК-1 – способность осуществлять педагогическую деятельность по профильным предметам (дисциплинам, модулям) в рамках программ основного общего и среднего общего образования, по программам дополнительного образования детей;
ПК-4 – способность вести научно-исследовательскую работу в области профильной дисциплины и методики ее преподавания;
ПК-6 – владение навыками участия в разработке и реализации различного типа проектов в образовательных организациях в педагогической сфере.
Задачи практики:
– формирование конкретных знаний, направленных на решение теоретических и практических задач в области элементарной математики;
– выработка умения формулировать суждения и выводы, логически последовательно и доказательно их излагать;
– адаптация теоретического математического материала из области «элементарной математики» для осуществления культурно-просветительской деятельности в области школьного математического образования.
Отчёт по практике состоит из введения, трёх заданий, заключения и списка использованных источников.
Задание 1. Работа с первоисточником
Изучение треугольника Паскаля весьма актуально в настоящее время, так как он часто встречается в разнообразных олимпиадных заданиях по математике.
В. А. Успенский в книге «Треугольник Паскаля» [1] изложил теорию и свойства теории треугольника Паскаля.
Фукс Д. и Фукс М. в работе «Арифметика биномиальных коэффициентов» [2] изложил свойства треугольника Паскаля и доказол их.
Галкин Е.В.@ Нестандартные задачи по математике. Задачи логического характера»[4] задачи на математическое и логическое мышление
Соловьева, О. А. «Комбинаторные приложения треугольника Паскаля» [4] задачи на математическое и логическое мышление.
Цель исследования – систематизировать и адаптировать теоретический и практический материал по теме «Треугольник Паскаля» для учащихся общеобразовательных школ.
Для достижения поставленной цели сформулируем и решим следующие задачи:
1. Локально упорядочить теоретический материал, связанный треугольником Паскаля.
2. Выявить и решить серию задач для школьников по теме «Треугольник Паскаля».
Отчет состоит из введения, двух разделов, заключения и списка из 3 использованных источников
Задание 2. Структурирование материала
Теоретическое обоснование основных положений темы «Треугольник Паскаля»
Рассмотрим какую-нибудь строчку чисел 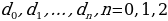 . Образуем из нее новую строчку чисел
. Образуем из нее новую строчку чисел 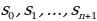 по следующему правилу:
по следующему правилу:
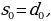 (1)
(1)
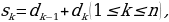 (2)
(2)
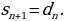 (3)
(3)
Про новую строчку будем говорить, что она получена из предыдущей по закону Паскаля.
Например, из строчки 2, 0, –2 по закону Паскаля получается строка 2, 2, –2, –2, а из этой, в свою очередь, 2, 4, 0, –4, –2.
З а м е ч а н и е 1. Если строчка 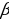 получена из строчки
получена из строчки 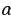 по закону Паскаля, то сумма членов строчки
по закону Паскаля, то сумма членов строчки 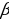 равна удвоенной сумме членов строчки
равна удвоенной сумме членов строчки 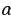 .
.
Действительно, если выполняются соотношения (1) – (3), то
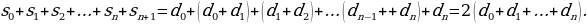 (4)
(4)
З а м е ч а н и е 2. Назовем строчку 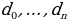 симметричной, если при любом целом k от 0 до n имеет место равенство
симметричной, если при любом целом k от 0 до n имеет место равенство
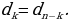 (5)
(5)
Строчка чисел 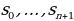 , получающаяся по закону Паскаля из симметричной точки
, получающаяся по закону Паскаля из симметричной точки 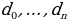 сама является симметричной.
сама является симметричной.
Рассмотрим строку, состоящую из одного числа – единицы. Назовем эту строку нулевой строкой Паскаля. Образуем из нее по закону Паскаля новую строку, которую назовем первой строкой Паскаля. Из первой строки Паскаля по закону Паскаля образуем вторую строку Паскаля и т.д. Поскольку при переходе к каждой следующей строке число членов этой строки возрастает на единицу, то в n-й строке Паскаля будет n+1 число. Из этого следует, что
сумма чисел n-й строки Паскаля равна 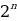 ;
;
все строки Паскаля симметричны.

Рисунок 1
Запишем строки Паскаля, начиная с нулевой, друг под другом, так чтобы каждое число каждый строки оказалось между теми числами предыдущей строки суммой которых оно является. Получаем бесконечную таблицу, называемую
арифметическим треугольником Паскаля, или
треугольником Паскаля (в соответствии с рисунком 1).
Члены каждой строки Паскаля обычно нумеруется слева направо, начиная с нулевого.
Обозначения: число, стоящее на k-м месте в n-й строке, будем обозначать через 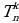 , так что, например,
, так что, например, 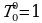 ,
, 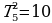 ,
, 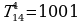 .
.
Свойства строк треугольника Паскаля:
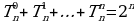 (6)
(6)
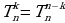 (7)
(7)
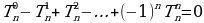 (8)
(8)
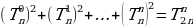 (9)
(9)
В силу своего определения числа 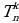 подчиняется следующему соотношениям:
подчиняется следующему соотношениям:
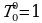 (10)
(10)
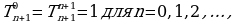 (11)
(11)
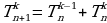 для n= 0, 1, 2,…; k = 1, 2,…, n. (12)
для n= 0, 1, 2,…; k = 1, 2,…, n. (12)
Пользуясь равенствами (10) – (12) можно построить сколько угодно строк треугольника Паскаля.
Треугольник Паскаля при расположении его членов, рассмотренном на рисунке 1, естественно называть треугольником Паскаля в равнобедренной форме, или короче равнобедренным треугольником Паскаля. Такую бесконечную таблицу естественно называют треугольником Паскаля в прямоугольной форме, или просто прямоугольным треугольником Паскаля. В прямоугольном треугольнике Паскаля на пересечении 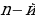 горизонтали и
горизонтали и 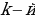 вертикали стоит число
вертикали стоит число 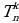 :
:
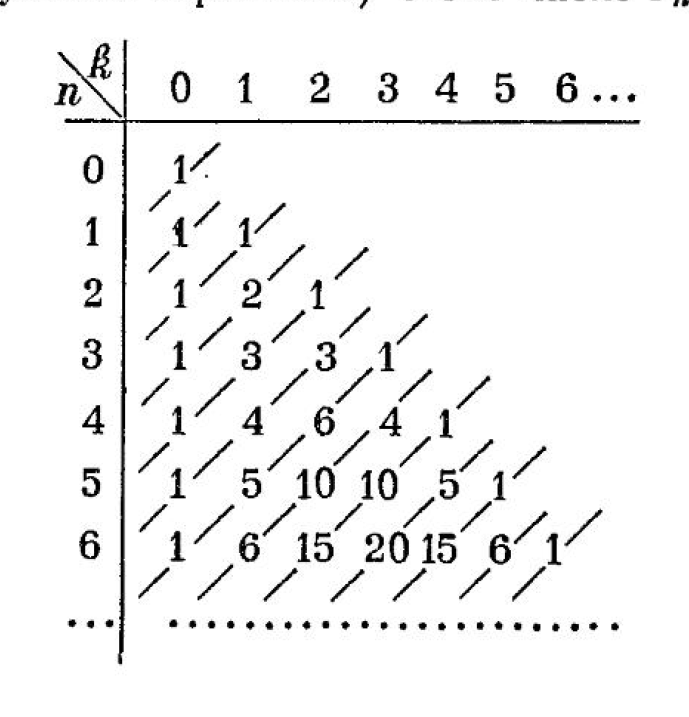
Рисунок 2
На 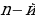 горизонтали здесь располагается
горизонтали здесь располагается 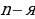 строка Паскаля; числа, стоящие на фиксированной вертикали, также достойны изучения. Помимо вертикалей и горизонталей, в прямоугольном треугольнике Паскаля легко прослеживаются диагонали. Различают восходящие и нисходящие диагонали. По главной нисходящие диагонали стоят единицы; по каждой из параллельных ей нисходящих диагоналей располагается – в силу симметрии строка Паскаля – та же последовательность чисел, что и по соответствующей вертикали; поэтому рассмотрение бесконечных рядов чисел, расположенных на нисходящих диагоналях, не дает ничего нового (рисунок 2).
строка Паскаля; числа, стоящие на фиксированной вертикали, также достойны изучения. Помимо вертикалей и горизонталей, в прямоугольном треугольнике Паскаля легко прослеживаются диагонали. Различают восходящие и нисходящие диагонали. По главной нисходящие диагонали стоят единицы; по каждой из параллельных ей нисходящих диагоналей располагается – в силу симметрии строка Паскаля – та же последовательность чисел, что и по соответствующей вертикали; поэтому рассмотрение бесконечных рядов чисел, расположенных на нисходящих диагоналях, не дает ничего нового (рисунок 2).
З а м е ч а н и е 3. Любое число (n+2)-й диагонали, кроме самых крайних единиц, являются суммой двух чисел, находящихся на двух предшествующих диагоналях, n-й и (n+1)-й.
Операции Паскаля
Задавшись произвольными п и k (n= О, 1, 2,…; k =О, 1,…n), можно, если располагать достаточными временем и терпением, найти 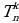 . Для этого надо начать выписывать треугольник Паскаля и продолжать до тех пор, пока мы не дойдем до k-го числа n-й строки. Или же можно просто воспользоваться соотношениями (12) эти соотношения позволят, совершив конечное число сложений, найти
. Для этого надо начать выписывать треугольник Паскаля и продолжать до тех пор, пока мы не дойдем до k-го числа n-й строки. Или же можно просто воспользоваться соотношениями (12) эти соотношения позволят, совершив конечное число сложений, найти 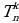 .
.
Задача.
Сколько сложений надо произвести, чтобы, применяя соотношения (12), вычислить 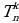
Операцию, состоящую в нахождении по числам п и k числа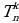 ., условимся называть операцией Паскаля. А если доопределить
., условимся называть операцией Паскаля. А если доопределить 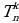 , так,
, так,
как было указано выше, то операция Паскаля будет определена для любого целого неотрицательного п и для любого целого k.
При помощи операции Паскаля легко записываются числа 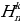 ., служащие ответом на олимпиадную задачу. С целью найти такую запись:
., служащие ответом на олимпиадную задачу. С целью найти такую запись:
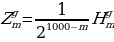 (14)
(14)
так что
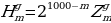 (15)
(15)
Тогда из соотношений (14) и (15) получаем
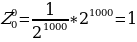 (16)
(16)
Подставим в соотношения (2), (4) и (3) вместо чисел 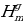 их выражения через
их выражения через 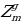 согласно (16). Мы получим из (2)
согласно (16). Мы получим из (2)
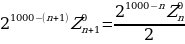 ,
,
откуда
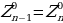 (17)
(17)
Точно так же мы получим из (4)
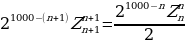 ,
,
откуда
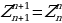 (18)
(18)
Наконец, из (3) мы получим
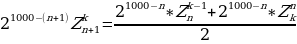 ,
,
откуда
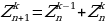 (19)
(19)
Равенства (18) — (519) показывают, что каждая строка
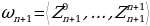
где n = 0, 1, .... 999, получается из предшествующей строки
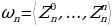
по закону Паскаля. Поскольку, как видно из равенства (16), начальная строка
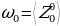
есть нулевая строка Паскаля, то следующая за ней строка 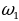 есть первая строка Паскаля, строка
есть первая строка Паскаля, строка 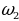 есть вторая строка Паскаля и т. д.; при каждом т от 0 до 1000’) строка
есть вторая строка Паскаля и т. д.; при каждом т от 0 до 1000’) строка 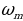 есть m-я строка Паскаля, и
есть m-я строка Паскаля, и
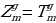 (20)
(20)
Следовательно, в силу (15), при каждом m = 0, 1, ... ,.., 1000 и каждом k=0, 1, ..., т
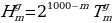 (21)
(21)
В частности,
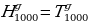 (22)
(22)
Итак, количества людей, пришедших на перекрестки тысячного ряда, суть не что иное, как члены тысячной же строки Паскаля. Если считать операцию Паскаля стандартной операцией, то равенство (522) даст решение задачи. В следующих двух параграфах мы увидим, как при помощи операции Паскаля можно найти решения двух важных задач [1].
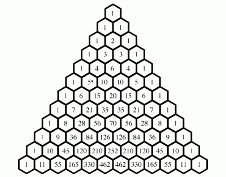
Основные свойства треугольника Паскаля [2]:
Каждое число равно сумме двух расположенных над ним чисел (рисунок 3). Треугольник можно продолжать неограниченно.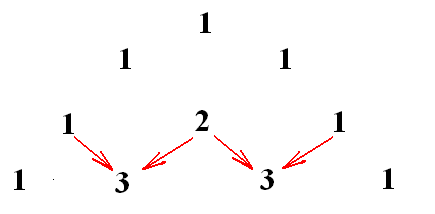
Рисунок 3
Первая диагональ треугольника Паскаля – это натуральные числа, идущие по порядку(рисунок 4).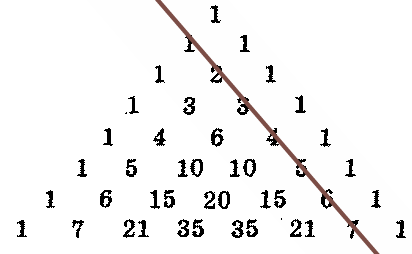
В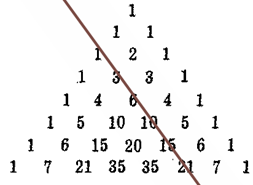
Рисунок 4
доль второй диагонали треугольника выстроены треугольные числа (Треугольное число — это число кружков, которые могут быть расставлены в форме правильного треугольника. Очевидно, с чисто арифметической точки зрения, n-е треугольное число — это сумма n первых натуральных чисел) и их обобщения на случай пространств всех размерностей (рисунок 5).
Рисунок 5
Т 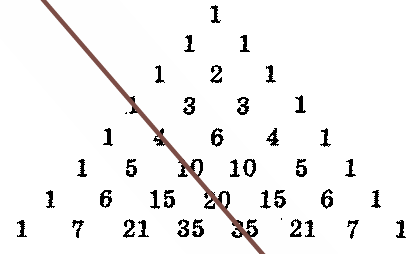
ретья диагональ треугольника Паскаля - это «пирамидальные» числа или, более точно, тетраэдральные числа, показывающие сколько шаров может быть уложено в виде треугольной пирамиды (тетраэдра) (рисунок 6).
Рисунок 6
Паскаль, наверное, не знал, что числа Фибоначчи скрыты в его треугольнике. Это обстоятельство было обнаружено только в XIX веке — элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, … в которой каждое последующее число равно сумме двух предыдущих чисел). Красным цветом выделены числа Фибоначчи. Сумма чисел n-й диагонали есть n-е число Фибоначчи (рисунок 7).
Рисунок 7
С 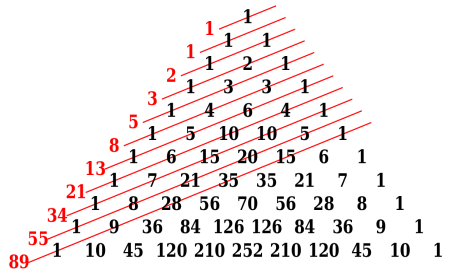
умма чисел, стоящих на четных местах, равна сумме чисел, стоящих на нечетных местах. Сумма чисел, стоящих в любой строке треугольника, вдвое больше суммы чисел, стоящей в предыдущей строке, поскольку при построении каждой строки числа, стоящие в предыдущей, сносятся дважды.
С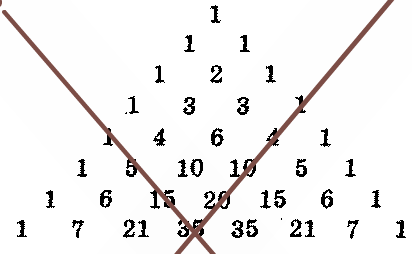
умма чисел первой (самой верхней) строки равна 1. Следовательно, суммы чисел, стоящих в строках треугольника Паскаля, образуют геометрическую прогрессию с первым членом, равным 1, и знаменателем 2: 1, 2, 4, 8, ...
Рисунок 8
К 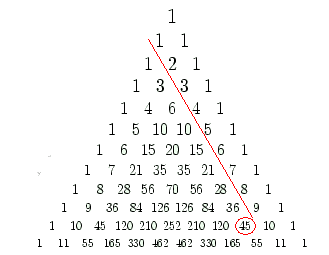
аждое число в таблице, будучи уменьшенным на единицу, равно сумме всех чисел, заполняющих пространство, ограниченный теми диагоналям, на пересечении которых стоит это число (рисунок 8). Каждое число треугольника Паскаля равно сумме предыдущей диагонали, стоящей над этим числом (рисунок 9).
Рисунок 9
Рисунок 10
Е 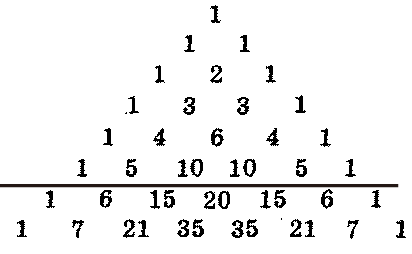
сли номер строки треугольника Паскаля – простое число, то все числа этой строки, кроме 1, делятся на это число (рисунок 10). Числа, стоящие на горизонтальных строках треугольника Паскаля, - это биномиальные коэффициенты, то есть коэффициенты разложения n (a+b) по степеням (рисунок 11).
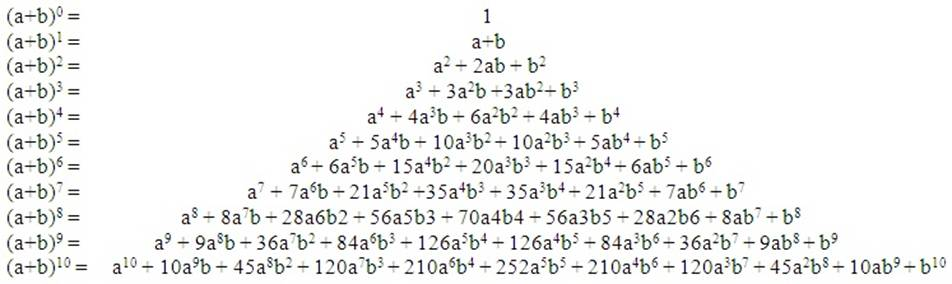
Рисунок 11
Задание 3. Методическая разработка по теме
Серия задач для школьников по теме «Треугольник Паскаля».
З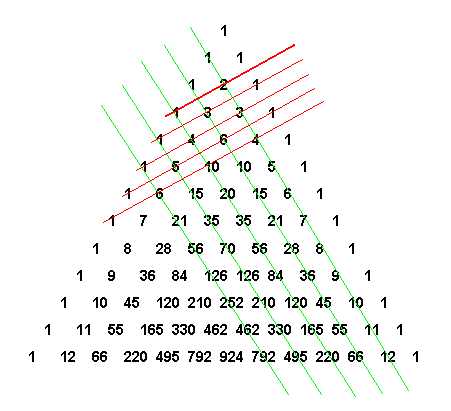 адача 1. В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
адача 1. В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
Решение:
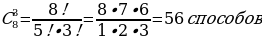


Рисунок 12
В треугольнике Паскаля число, показывающее, сколькими способами можно выбрать
k элементов из множества, содержащего
n различных элементов, стоит на пересечении
k-ой диагонали и
n-ой строки.

Нужно найти диагональ восьмую сверху и отсчитать три числа по горизонтали. Получим число 56 (рисунок 12).
Задача 2. Из шести врачей поликлиники двух необходимо отправить на курсы повышения квалификации. Сколькими способами это можно сделать?
Решение: 
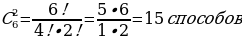
Н
Рисунок 13
ужно найти диагональ шестую сверху и отсчитать два числа по горизонтали. Получим число 15 (рисунок 13).
Задача 3. В пачке находятся одинаковые по размеру 7 тетрадей в линейку и 5 в клетку. Из пачки наугад берут 3 тетради. Какова вероятность того, что все три тетради окажутся в клетку?
Решение. Сначала найдём общее число возможных исходов, т.е. сколькими способами мы можем выбрать 3 тетради из 12 тетрадей
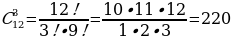

А сколькими способами мы можем выбрать 3 тетради в клетку из имеющихся 5 тетрадей?
сколькими способами мы можем выбрать 3 тетради в клетку из имеющихся 5 тетрадей?
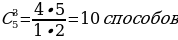
В
Рисунок 14
ероятностью Р наступления случайного события А называется отношение
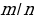
где n – число всех возможных исходов эксперимента, а m – число всех благоприятных исходов:
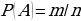
.
По формуле нахождения вероятности получим (рисунок 14).
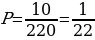
Задача 4. В кондитерском магазине продавались 4 сорта пирожных: э
клеры, песочные, наполеоны и слоеные. Сколькими способами можно купить 7 пирожных?
Решение: Покупка не зависит от того, в каком порядке укладывают купленные пирожные в коробку. Покупки будут различными, если они отличаются количеством купленных.
Рисунок 15
Следовательно, будем применять формулу сочетания с повторениями:
далее составляем треугольник Паскаля и найдем по нему решение для
числа сочетания 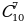 , где 7- диагональ, а 10 – строка. Их пересечение и будет нашим ответом (рисунок 15).
, где 7- диагональ, а 10 – строка. Их пересечение и будет нашим ответом (рисунок 15).
Ответ: 120 способов.
Задача 5. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти цветов?
Р
ешение: для решение данной задачи будем учитывать такие условия как все цвета различны, важен порядок и количество. Исходя из этого для решения данной задачи мы будем использовать формулу размещения без повторений:
Рисунок 16
Найдем по треугольнику Паскаля значение сочетания
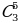
, где 3 - диагональ, 5- строка. Полученный ответ умножим на 3!. Произведение и будет нашим конечным ответом к задаче (рисунок 16).
При пересечении мы получили число 10. Далее считаем 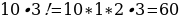 .
.
О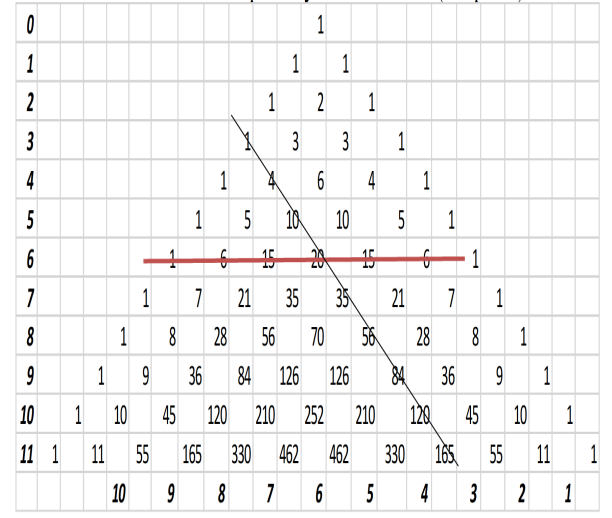
твет: 60 способов.
Задача 6. В магазине «Теплица» продается 6 различных сортов помидор. Сколькими способами можно выбрать из них 3 сорта помидор?
Рисунок 17
Решение: В данной задаче нам даны различные сорта, поэтому повторений не будет и порядок выбора сортов нам не важен, нам важно количество.
Следовательно, будем использовать формулу сочетаний без повторений для решения данной задачи.
Найдем решение с помощью нашего треугольника Паскаля, в котором пересечении 3-й диагонали и 6 строки будет наш ответ (рисунок 17).
Задача 7. Почему равенства 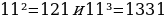 похожи на строчки треугольника Паскаля? Чему равно 114?
похожи на строчки треугольника Паскаля? Чему равно 114?
Решение
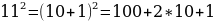 ;
;
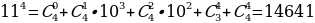
Ответ: 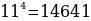 [3]
[3]
Задача 8. Сколько разных видов блинчиков может предложить «Матрена», исключая размеры блинчиков или их количество?
Решение. Начинки для каждого блинчика являются элементами подмножества множества всех возможных начинок, а пустое множество это блинчик без начинки. Общее число всевозможных блинчиков будет равно.
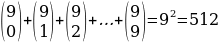
Таким образом, «Матрена» может предложить 512 различных блинчиков.
З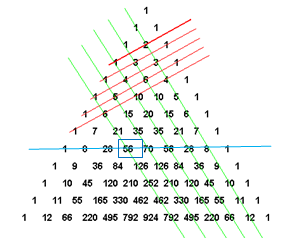
адача 9. На почте выставлены на продажу 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора? [4].
Решение:
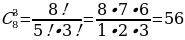 способов.
способов.
Рисунок 18
В треугольнике Паскаля число, показывающее, сколькими способами можно выбрать k элементов из множества, содержащего n различных элементов, стоит на пересечении k-ой диагонали и n-ой строки. Найдем восьмую диагональ сверху и отсчитаем три числа по горизонтали (рисунок 18).
Ответ: 56 способов

Рисунок 19
Задача 10. В город А можно попасть по единственному входу. На каждом перекрестке дорога расходится на две. В город вошли 2
10 человек. На каждом п
ерекрестке они делятся пополам. Сколько человек окажется на каждом перекрестке, когда они уже не смогут разделиться [4]?
Ответ:1,10,45,120,
210,252,210,120,45,
10,1ч.
ЗАКЛЮЧЕНИЕ
Основные выводы по практике.
В работе была дана общая характеристика треугольника как геометрической фигуры, был детально рассмотрен треугольник Паскаля, его свойства.
Одной из наиболее известных и изящных численных схем во всей математике является треугольник Паскаля. Треугольник Паскаля – понятие значительно шире, чем мне представлялось. Он обладает не только удивительными свойствами, но и применялся в архитектуре средних веков для построения схем пропорциональности и для построения прямых углов землемерами и архитекторами. Используя треугольник Паскаля, можно решить задачи из теории вероятности и комбинаторики. С комбинаторными задачами я встречалась на уроках математики в 6 классе и при решении олимпиадных задач.
Треугольник Паскаля применяется в курсе алгебры, при решении комбинаторных задач, для решения различных задач в области физики, а с появлением вычислительных машин построение треугольника Паскаля стало излюбленной задачкой для начинающих при изучении основ программирования.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.
Успенский, В.А. Треугольник Паскаля / В. А. Успенский. – 2-е изд. – Москва : Наука, 1979. – 48 с.
Фукс, Д. Арифметика биномиальных коэффициентов / Д. Фукс, М. Фукс // Квант. – 1970. – № 6. – С.17-25.
Галкин Е.В. Нестандартные задачи по математике. Задачи логического характера. Книга для учащихся 5-11кл. / Е. В. Галкин. Москва, «Просвещение», 1996г. – 194 с.
Соловьева, О. А. Комбинаторные приложения треугольника Паскаля / О. А. Соловьева // Молодой ученый. — 2016. — № 11 (115). — С. 75-79







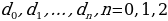 . Образуем из нее новую строчку чисел
. Образуем из нее новую строчку чисел 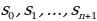 по следующему правилу:
по следующему правилу: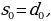 (1)
(1)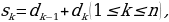 (2)
(2)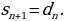 (3)
(3)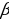 получена из строчки
получена из строчки 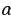 по закону Паскаля, то сумма членов строчки
по закону Паскаля, то сумма членов строчки 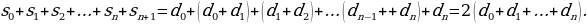 (4)
(4)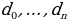 симметричной, если при любом целом k от 0 до n имеет место равенство
симметричной, если при любом целом k от 0 до n имеет место равенство 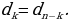 (5)
(5)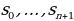 , получающаяся по закону Паскаля из симметричной точки
, получающаяся по закону Паскаля из симметричной точки 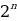 ;
;
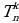 , так что, например,
, так что, например, 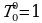 ,
, 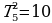 ,
, 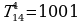 .
.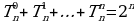 (6)
(6)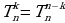 (7)
(7)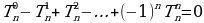 (8)
(8)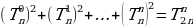 (9)
(9)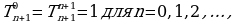 (11)
(11)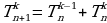 для n= 0, 1, 2,…; k = 1, 2,…, n. (12)
для n= 0, 1, 2,…; k = 1, 2,…, n. (12)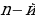 горизонтали и
горизонтали и 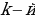 вертикали стоит число
вертикали стоит число 
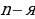 строка Паскаля; числа, стоящие на фиксированной вертикали, также достойны изучения. Помимо вертикалей и горизонталей, в прямоугольном треугольнике Паскаля легко прослеживаются диагонали. Различают восходящие и нисходящие диагонали. По главной нисходящие диагонали стоят единицы; по каждой из параллельных ей нисходящих диагоналей располагается – в силу симметрии строка Паскаля – та же последовательность чисел, что и по соответствующей вертикали; поэтому рассмотрение бесконечных рядов чисел, расположенных на нисходящих диагоналях, не дает ничего нового (рисунок 2).
строка Паскаля; числа, стоящие на фиксированной вертикали, также достойны изучения. Помимо вертикалей и горизонталей, в прямоугольном треугольнике Паскаля легко прослеживаются диагонали. Различают восходящие и нисходящие диагонали. По главной нисходящие диагонали стоят единицы; по каждой из параллельных ей нисходящих диагоналей располагается – в силу симметрии строка Паскаля – та же последовательность чисел, что и по соответствующей вертикали; поэтому рассмотрение бесконечных рядов чисел, расположенных на нисходящих диагоналях, не дает ничего нового (рисунок 2).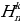 ., служащие ответом на олимпиадную задачу. С целью найти такую запись:
., служащие ответом на олимпиадную задачу. С целью найти такую запись: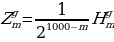 (14)
(14)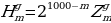 (15)
(15)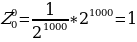 (16)
(16)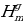 их выражения через
их выражения через 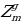 согласно (16). Мы получим из (2)
согласно (16). Мы получим из (2)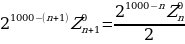 ,
,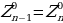 (17)
(17)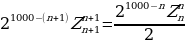 ,
,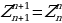 (18)
(18)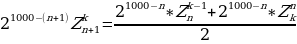 ,
,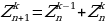 (19)
(19)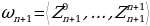
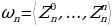
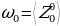
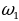 есть первая строка Паскаля, строка
есть первая строка Паскаля, строка 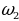 есть вторая строка Паскаля и т. д.; при каждом т от 0 до 1000’) строка
есть вторая строка Паскаля и т. д.; при каждом т от 0 до 1000’) строка 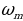 есть m-я строка Паскаля, и
есть m-я строка Паскаля, и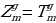 (20)
(20)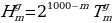 (21)
(21)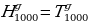 (22)
(22)







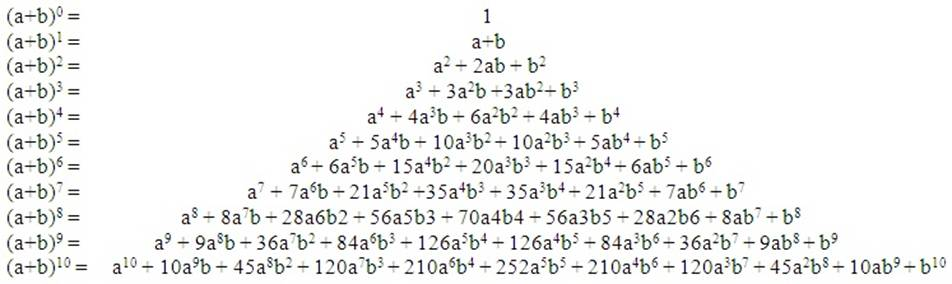
 адача 1. В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
адача 1. В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?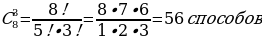




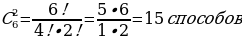
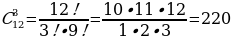
 сколькими способами мы можем выбрать 3 тетради в клетку из имеющихся 5 тетрадей?
сколькими способами мы можем выбрать 3 тетради в клетку из имеющихся 5 тетрадей?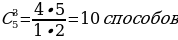

 где n – число всех возможных исходов эксперимента, а m – число всех благоприятных исходов:
где n – число всех возможных исходов эксперимента, а m – число всех благоприятных исходов: 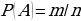 .
. 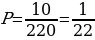

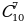 , где 7- диагональ, а 10 – строка. Их пересечение и будет нашим ответом (рисунок 15).
, где 7- диагональ, а 10 – строка. Их пересечение и будет нашим ответом (рисунок 15).
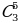 , где 3 - диагональ, 5- строка. Полученный ответ умножим на 3!. Произведение и будет нашим конечным ответом к задаче (рисунок 16).
, где 3 - диагональ, 5- строка. Полученный ответ умножим на 3!. Произведение и будет нашим конечным ответом к задаче (рисунок 16). 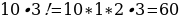 .
.
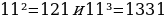 похожи на строчки треугольника Паскаля? Чему равно 114?
похожи на строчки треугольника Паскаля? Чему равно 114?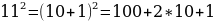 ;
;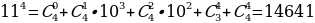
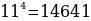 [3]
[3]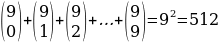

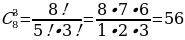 способов.
способов.











