Гомельская областная научно-практическая конференция учащихся
по естественно-научным и социально-гуманитарным направлениям
«Поиск»
Отдел образования, спорта и туризма Ельского райисполкома
ГУО «Движковский ясли-сад-базовая школа Ельского района»
Секция «Математика»
«Формула Пика»
Учебно-исследовательская работа
Выполнила
Тимощенко Наталья Леонидовна, учащаяся 9 класса
Руководитель
Черепанова Татьяна Михайловна учитель математики
Движки, 2019
Введение
Ни для кого не секрет, что изучение геометрии доставляет немало трудностей: необходимо знать не только определения понятий, их свойства и признаки, но «держать» в голове много различных формул. Изучая тему «Площади многоугольников», я задалась вопросом «Существует ли способ нахождения площадей, отличные от тех, которые мы изучали на уроках?»
Чтобы вычислить площадь изображённой фигуры, необходимо сделать дополнительные построения: разбить данную фигуру на несколько треугольников и прямоугольник, провести высоту в треугольнике. Возникли вопросы: в чём заключается особенность таких задач, существуют ли специальные методы и приёмы решения задач на вычисление площади фигур, изображённых на клетчатой бумаге.
Изучая литературу по данной теме, я нашла формулу Пика. Эта формула меня заинтересовала. Решив несколько задач используя данную формулу, пришла к выводу, что задачи решаются быстрее и легче. В связи с этим возникла гипотеза о том, что задачи на нахождение площади фигур, изображённых на клетчатой бумаге, с помощью формулы Пика можно решить более рационально.
Объект исследования: формула Пика.
Предмет исследования: рациональность применения формулы Пика при решении задач.
Цель работы: обосновать рациональность использования формулы Пика при решении задач на нахождение площади фигур, изображённых на клетчатой бумаге.
Задачи:
изучить литературу по данной теме.
прорешать задачи на нахождение площади фигур, изображённых на клетчатой бумаге геометрическим методом.
прорешать задачи на нахождение площади фигур, изображённых на клетчатой бумаге, используя формулу Пика.
сравнить и проанализировать результаты исследования.
Методы исследования: сравнение, обобщение.
Актуальность данного исследования состоит в том, что усвоение формулы может помочь школьникам быстро и легко решать задачи на вычисление площади различных фигур на клетчатой бумаге. При решении задач на клетчатой бумаге нам не понадобится знание основ планиметрии, а будут нужны именно смекалка, геометрическое воображение и достаточно простые геометрические сведения, которые известны всем.
Также при решении таких задач возникает ощущение математических открытий на уровне, доступном каждому ученику.
Теоретическая часть
К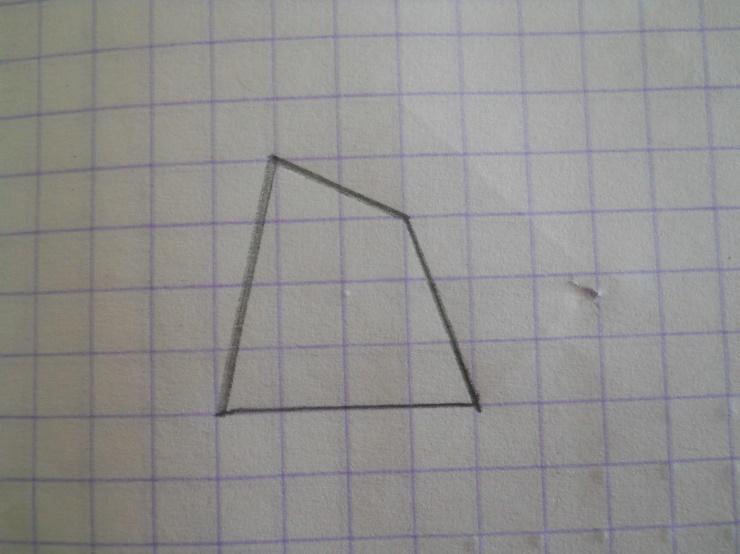 летчатая бумага (точнее — ее узлы), на которой мы часто предпочитаем рисовать и чертить, является одним из важнейших примеров точечной решетки на плоскости. Нарисуем на клетчатой бумаге какой-нибудь многоугольник (рисунок 1). Попробуем теперь рассчитать его площадь. Как это сделать? Наверное, проще всего разбить его на прямоугольные треугольники и трапецию, площади которых уже нетрудно вычислить и сложить полученные результаты.
летчатая бумага (точнее — ее узлы), на которой мы часто предпочитаем рисовать и чертить, является одним из важнейших примеров точечной решетки на плоскости. Нарисуем на клетчатой бумаге какой-нибудь многоугольник (рисунок 1). Попробуем теперь рассчитать его площадь. Как это сделать? Наверное, проще всего разбить его на прямоугольные треугольники и трапецию, площади которых уже нетрудно вычислить и сложить полученные результаты.
И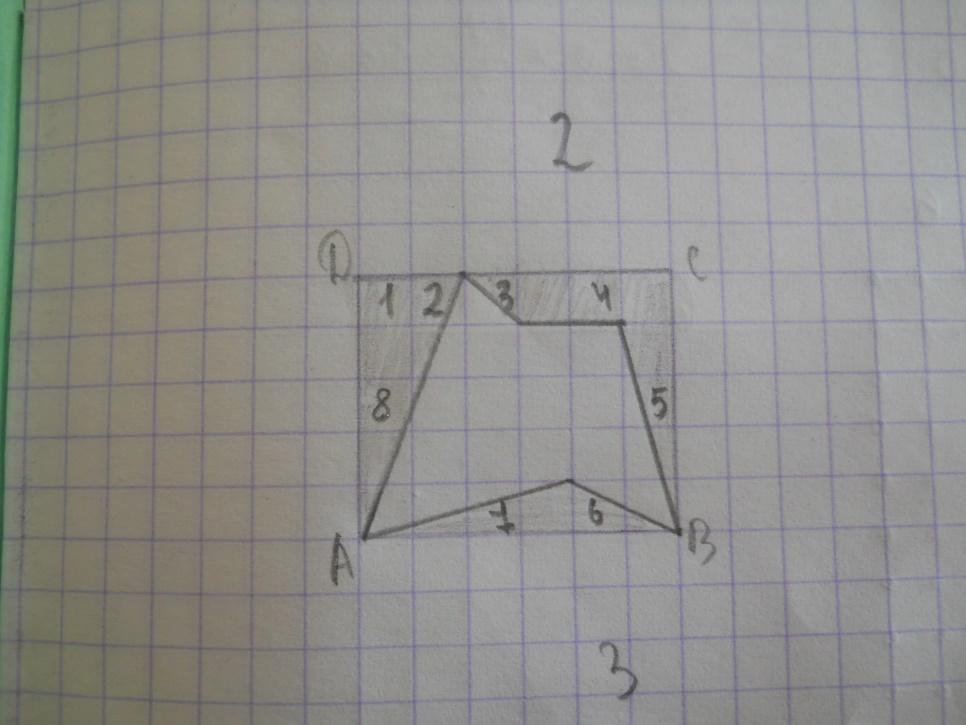 спользованный способ несложен, но очень громоздок, кроме того он годится не для всяких многоугольников. Так следующий многоугольник нельзя разбить на прямоугольные треугольники, так как мы это проделали в предыдущем случае (рисунок 2). Можно, например, попробовать дополнить его до «хорошего», нужного нам, то есть до такого, площадь которого мы сможем вычислить описанным способом, потом из полученного числа вычесть площади добавленных частей.
спользованный способ несложен, но очень громоздок, кроме того он годится не для всяких многоугольников. Так следующий многоугольник нельзя разбить на прямоугольные треугольники, так как мы это проделали в предыдущем случае (рисунок 2). Можно, например, попробовать дополнить его до «хорошего», нужного нам, то есть до такого, площадь которого мы сможем вычислить описанным способом, потом из полученного числа вычесть площади добавленных частей.
Однако оказывается, что есть очень простая формула, позволяющая вычислить площади таких многоугольников с вершинами в узлах квадратной сетки:
S = B + 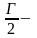 1, где
1, где
S - площадь многоугольника, выраженная в площадях единичных квадратиков сетки,
Г – количество узлов сетки, лежащих на границах многоугольника,
В – количество узлов сетки, лежащих внутри многоугольника.
Эту формулу открыл австрийский математик Пик Георг Александров (1859 – 1943 г.г.) в 1899 году. Кроме этой формулы Георг Пик открыл теоремы Пика, Пика–Жюлиа, Пика – Невалины, доказал неравенство Шварца–Пика.
Эта формула оставалась незамеченной в течение некоторого времени после того, как Пик её опубликовал, однако в 1949 г. польский математик Гуго Штейнгауз включил теорему в свой знаменитый «Математический калейдоскоп». С этого времени теорема Пика стала широко известна. В Германии формула Пика включена в школьные учебники [2].
Доказательство формулы Пика
1. Экспериментальное доказательство, что формула Пика верна для фигур:
1) без узлов внутри и на сторонах,
2) с узлами на сторонах,
3) с узлами внутри и на сторонах.
Доказательство производится в несколько этапов: от самых простых фигур до произвольных многоугольников:
б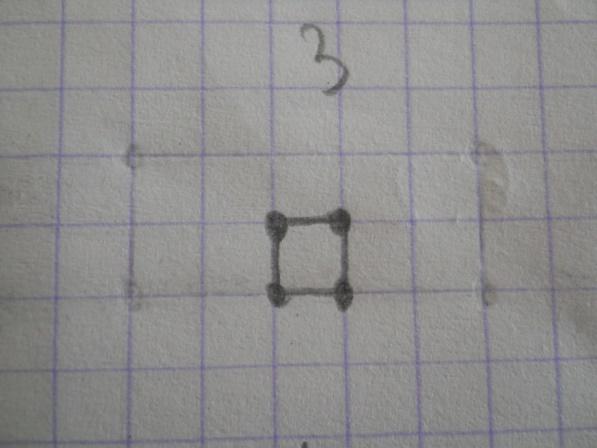 ез узлов внутри и на сторонах.
ез узлов внутри и на сторонах.
Доказательство: Рассмотрим единичный квадрат. В самом деле, для него  = 1, В = 0, Г= 4, и формула верна.
= 1, В = 0, Г= 4, и формула верна.
S = В + 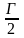 - 1.
- 1.
S=0+ 4/2 - 1 =1
с узлами на сторонах.
Д оказательство: Рассмотрим произвольный прямоугольник со сторонами, параллельными осям координат. Его площадь – это произведение длины и ширины, т.е. S = 1*10 = 10. Для доказательства формулы посчитаем В = 0, Г = 22. Непосредственной подстановкой убеждаемся, что формула Пика верна.
оказательство: Рассмотрим произвольный прямоугольник со сторонами, параллельными осям координат. Его площадь – это произведение длины и ширины, т.е. S = 1*10 = 10. Для доказательства формулы посчитаем В = 0, Г = 22. Непосредственной подстановкой убеждаемся, что формула Пика верна.
S = 0 + 22\2 – 1= 10
с узлами внутри и на сторонах.
Д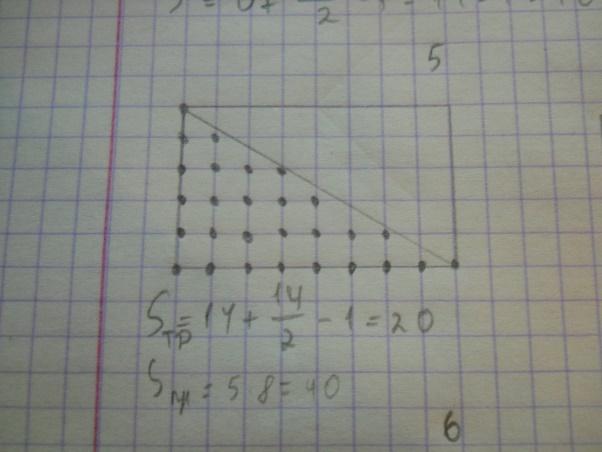 оказательство: Рассмотрим прямоугольный треугольник с катетами, параллельными осям координат.
оказательство: Рассмотрим прямоугольный треугольник с катетами, параллельными осям координат.
S = 5*8 = 40. Для проверки формулы Пика посчитаем: В=14, Г=14, тогда имеем: S=14+14/2–1=20. Формула Пика верна для такого треугольника.
Практическая часть
Нахождение площади фигур
геометрическим методом и по формуле Пика
Я решила убедиться в том, что формула Пика верна для разных многоугольников с вершинами в узлах сетки.
Оказывается, что если многоугольник можно разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.
Я рассмотрела некоторые задачи на клетчатой бумаге с клетками размером 1см 1см и провела сравнительный анализ по решению задач (Таблица№1).
1см и провела сравнительный анализ по решению задач (Таблица№1).
Таблица №1. Решение задач различными способами.
|
| Рисунок | По формуле геометрии | По формуле Пика |
| Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1. 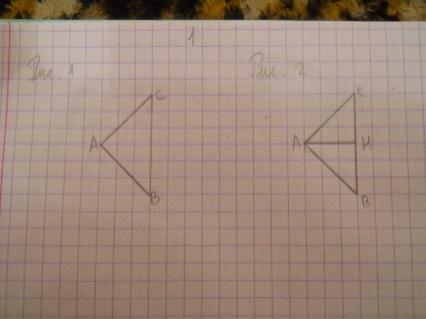
| Решение 1. Заметим, что данный треугольник ABC является прямоугольным (A = 90о). Воспользуемся тем, что диагональ квадратной клетки со сторонами, равными 1, равна 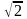 . Тогда катеты AB и AC данного треугольника будут равны . Тогда катеты AB и AC данного треугольника будут равны 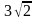 . Так как площадь прямоугольного треугольника равна половине произведения его катетов, то площадь данного треугольника будет равна 9. (Рис.1) . Так как площадь прямоугольного треугольника равна половине произведения его катетов, то площадь данного треугольника будет равна 9. (Рис.1) Решение 2. Проведем высоту AH. Тогда BC = 6, AH = 3 и, следовательно, S = 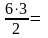 9. (Рис.2) Ответ: 9 . 9. (Рис.2) Ответ: 9 .
| Г = 12, В = 4, S = В + Г/2 – 1. S = 4 + 12/2 – 1 = 9. Ответ: 9.
|
| Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1. 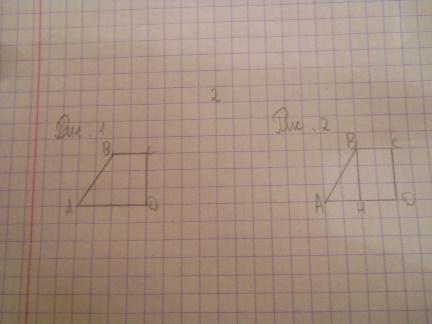
| Решение 1. Основания AD и BC данной трапеции равны соответственно 4 и 2. Высотой является боковая сторона CD = 3. Так как площадь трапеции равна произведению полусуммы оснований на высоту, то Sтр = 9. (Рис.1) Решение 2. Из точки B опустим перпендикуляр BH на AD. Он разобьет трапецию на прямоугольный треугольник ABH и прямоугольник HBCD. Катеты прямоугольного треугольника равны 2 и 3, следовательно, его площадь равна 3. Смежные стороны прямоугольника равны 2 и 3, следовательно, S = 6. Sтрап = Sтр + Sпр = 9. (Рис.2) Ответ. 9. | Г = 10, В = 5, S = В + Г/2 – 1. S = 5 + 10/2 – 1 =9. Ответ: 9.
|
3 | Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1.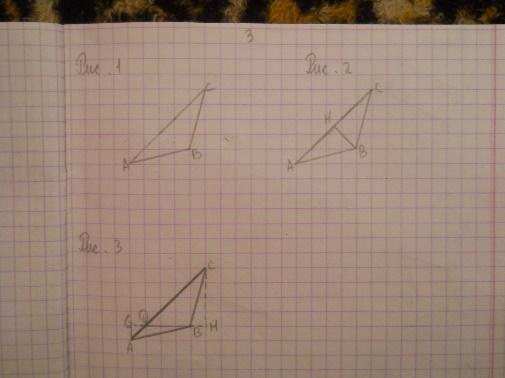 | Решение 1. Так как диагональ квадрата со стороной 1 равна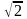 , то сторона AC треугольника ABC равна 5√2, высота BH, проведенная к этой стороне, равна 3√2/2. Следовательно, площадь данного треугольника равна 7,5. (Рис.2) , то сторона AC треугольника ABC равна 5√2, высота BH, проведенная к этой стороне, равна 3√2/2. Следовательно, площадь данного треугольника равна 7,5. (Рис.2) Решение 2. Разобьем данный треугольник ABC на два треугольника ABD и BDC. Их общая сторона BD равна 3, а высоты, к ней проведенные, равны соответственно 1 и 4. Площадь треугольника ABD равна 1,5, а площадь треугольника BDC равна 6. Площадь треугольника ABC равна сумме площадей этих треугольников и, следовательно, равна 7,5. (Рис.3). Ответ: 7,5. | Г = 7, В = 5, S = В + Г/2 – 1. S = 5 + 7/2 – 1= 7,5 Ответ: 7,5.
|
| Н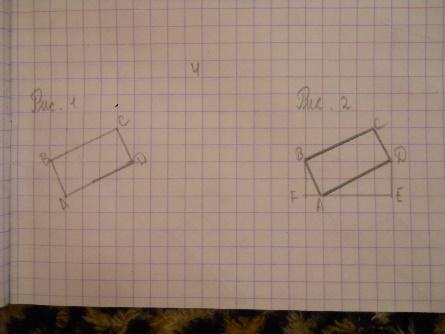 айдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1. айдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1. 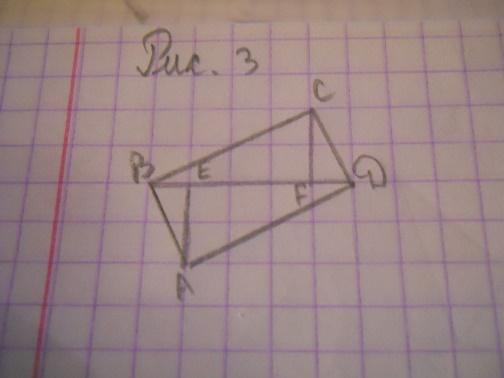
| Решение 1. Рассмотрим прямоугольный треугольник ADE. Катет AE равен 4, катет DE равен 2. Следовательно, по теореме Пифагора гипотенуза AD равна 2√5. Аналогично, для прямоугольного треугольника ABF катет AF равен 1, катет BF равен 2. Следовательно, гипотенуза AB равна √5. Площадь данного прямоугольника равна произведению его соседних сторон, т.е. равна 10. Решение 2. Разобьем данный прямоугольник ABCD на два треугольника ABD и BCD. Сторона BD у них общая и равна 5. Высоты AE и CF, опущенные на эту сторону, равны 2. Так как площадь треугольника равна половине произведения стороны на высоту, опущенную на эту сторону, то площадь каждого из этих двух треугольников будет равна 5 и, следовательно, Sпр = 10. Ответ. 10. | Г = 6, В = 8, S = В + Г/2 – 1, S = 8 + 6/2 – 1 = 10 Ответ: 10. |
| 5 | Найдите площадь ромба ABCD, считая стороны квадратных клеток равными 1. 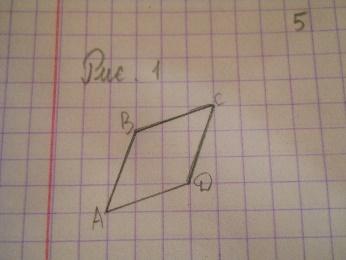
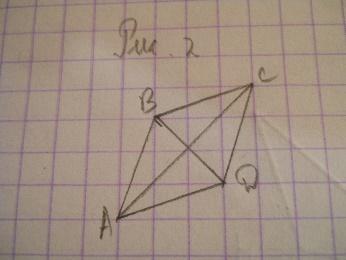 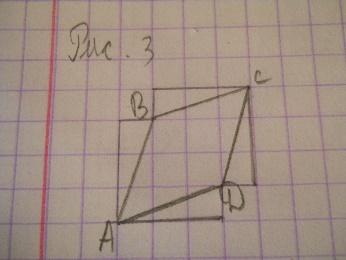
| Решение 1. Напомним, что площадь ромба равна половине произведения его диагоналей. Воспользуемся тем, что диагональ квадратной клетки со сторонами, равными 1, равна √2. Тогда диагонали АС и BD данного ромба будут равны соответственно 2√2 и 4√2, а его площадь будет равна 8. (Рис.2) Решение 2. Достроим на сторонах ромба четыре равных прямоугольных треугольника, катеты которых равны 1 и 3. Площадь каждого такого треугольника равна 1,5. Ромб вместе с этими треугольниками образует фигуру, состоящую из четырнадцати единичных квадратов. Следовательно, ее площадь равна 14. Вычитая из нее площадь четырех треугольников, получим, что площадь ромба равна 8. (Рис.3) Ответ. 8. | Г = 4, В = 7, S = В + Г/2 – 1. S = 7+4/2-1 = 8 Ответ: 8.
|
| 6 | Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1. 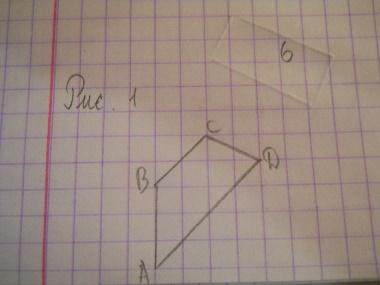
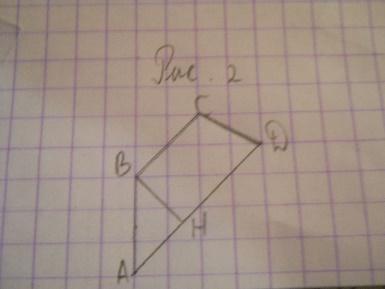
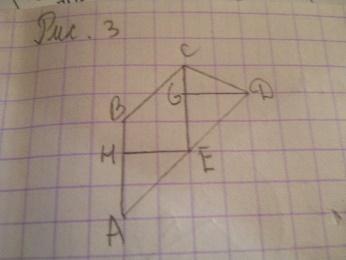
| Решение 1. Основания AD и BC трапеции равны соответственно 2√2 и 4√2. Высота BH трапеции равна 3√2/2. Так как площадь трапеции равна произведению полусуммы оснований на высоту, то площадь данной трапеции будет равна 9. (Рис.2) Решение 2. Разобьем трапецию на параллелограмм ABCE и треугольник CDE. (Рис.3). Сторона AB параллелограмма ABCE равна 3, высота EH, к ней проведенная, равна 2, следовательно, площадь этого параллелограмма равна 6. Сторона CE треугольника CDE равна 3, высота DG, к ней проведенная, равна 2, следовательно, площадь этого треугольника равна 3. Площадь трапеции равна сумме площадей параллелограмма и треугольника и, следовательно, равна 9. Ответ. 9. | Г=10, В =5, S = В + Г/2 – 1. S = 5+10/2-1 = 9 Ответ: 9.
|
| 7 | Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1. 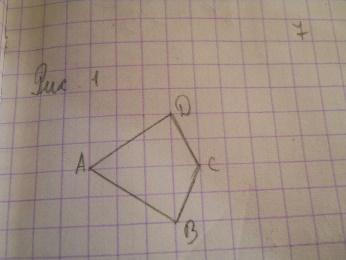
| Решение 1. Разобьем данный четырехугольник на два треугольника ABC и ACD. Сторона AC у них общая и равна 4. Высоты BH и DH равны 2. Следовательно, площади этих треугольников равны 4 и, значит, площадь четырехугольника равна 8. (рис.2) Решение 2. Разобьем данный четырехугольник на два треугольника ABD и BCD. Сторона BD у них общая и равна 4. Высоты AH и CH равны соответственно 3 и 1. Следовательно, площади этих треугольников равны соответственно 6 и 2. Значит, площадь четырехугольника равна 8. Ответ. 8. | 7. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1. Г= 4, В= 7, S = В + Г/2 – 1. S =7 + 4/2 – 1= 8 Ответ: 8.
|
| 8 | Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.
| Решение 1. Разобьем данный четырехугольник на два треугольника ACB и ACD. Сторона AC у них общая и равна 2√2. Высоты BH и DH равны 3√2/2. Следовательно, площади этих треугольников равны 3. Значит, SABCD =6. (Рис.2) Решение 2. Площадь данного четырехугольника равна разности площадей треугольников ABD и CBD. В треугольнике ABD сторона BD равна 3√2, высота AH = 5√2/2. Следовательно, его площадь равна 7,5. В треугольнике CBD сторона BD равна 3√2, высота CH равна √2/2. Следовательно, его площадь равна 1,5. Таким образом, SABCD =6/ Ответ: 6. | Г= 4, В= 5, S = В + Г/2 – 1, S = 5 + 4/2 – 1= 6 Ответ: 6. |
| 9 | Найдите площадь S сектора, считая стороны квадратных клеток равными 1. В ответе укажите S/π.
| Решение 1. Напомним, что площадь S кругового сектора вычисляется по формуле , где R – радиус круга,  - градусная величина угла сектора. В нашем случае - градусная величина угла сектора. В нашем случае  = 90о. Радиус R равен √5. Подставляя данные значения в формулу площади сектора, получим S = 5π/4. Откуда S/π=1,25. = 90о. Радиус R равен √5. Подставляя данные значения в формулу площади сектора, получим S = 5π/4. Откуда S/π=1,25. Решение 2. Заметим, что данный сектор является одной четвертой частью круга и, следовательно, его площадь равна одной четвертой площади круга. Площадь круга равна π R2, где R – радиус круга. В нашем случае R =√5 и, следовательно, площадь S сектора равна 5π/4. Откуда S/π=1,25. Ответ. 1,25. | 9. Найдите площадь S сектора, считая стороны квадратных клеток равными 1. В ответе укажите  . . Г= 5, В= 2, S = В + Г/2 – 1= 2 + 5/2 – 1= 3,5,  ≈ 1,11 ≈ 1,11 Ответ: ≈ 1,11.
|
| 10 | Н айдите площадь S кольца, считая стороны квадратных клеток равными 1. В ответе укажите  . .
| Решение. Площадь кольца равна разности площадей внешнего и внутреннего кругов. Радиус R внешнего круга равен 2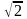 , радиус r внутреннего круга равен 2. Следовательно, площадь S кольца равна 4 , радиус r внутреннего круга равен 2. Следовательно, площадь S кольца равна 4 и, следовательно, и, следовательно,  . . Ответ:4. | Г= 8, В= 8, S = В + Г/2 – 1, S = 8 + 8/2 – 1=11,  ≈ 3,5 ≈ 3,5
Ответ: ≈3,5.
|
|
| Из решения задач №9 и №10 видим, что применение формулы Пика к фигурам, которые не являются многоугольниками, даёт приближённый результат. |
Нахождение площади поверхности пространственных форм
Проверим применимость этой формулы к пространственным формам.
Найти площадь полной поверхности прямоугольного параллелепипеда, считая стороны квадратных клеток равными 1.
К сожалению, подсчитать количество узлов решетки, попавших на границу параллелепипеда и внутрь параллелепипеда нельзя. Поэтому вычислить площадь полной поверхности по формуле Пика невозможно.
Это недостаток формулы.
Проанализировав способы решения задач, можно сделать следующие выводы:
Формула Пика даёт быстрое и простое решение задач на нахождение площади фигуры, вершины которой лежат в узлах решётки, то есть нахождения площадей многоугольников.
Использование формулы Пика для нахождения площади кругового сектора или кольца нецелесообразно, так как она даёт приближённый результат.
Формула Пика не применяется для решения задач в пространстве.
Из рассмотренных решений задач я увидела, что некоторые из них, легче решить, применяя геометрические формулы, так как высоту и основание можно определить по рисунку. Но в большинстве задач требуется разбиение фигуры на более простые или достраивание до прямоугольника, квадрата.
Из решения задач №9 и №10 я увидела, что применение формулы Пика к фигурам, которые не являются многоугольниками, даёт приближённый результат.
Для того чтобы проверить рациональность применения формулы Пика, я провела исследование на предмет затраченного времени (Приложение 1, таблица №2).
Вывод: решение задач с помощью формулы Пика, времени затрачивается гораздо меньше.
Заключение
В результате моей работы я расширила свои знания о решении задач на клетчатой бумаге, определила для себя классификацию исследуемых задач.
При выполнении работы были решены задачи на нахождение площади многоугольников, изображённых на клетчатой бумаге двумя способами: геометрическим и с помощью формулы Пика.
Анализ решений и эксперимент по определению затраченного времени показал, что применение формулы даёт возможность решать задачи на нахождение площади многоугольника, более рационально. Это позволяет экономить время на уроках математики.
Нахождение площади различных фигур, изображённых на клетчатой бумаге, позволило сделать вывод, что использование формулы Пика для вычисления площади кругового сектора и кольца нецелесообразно, так как она даёт приближённый результат, и, что формула Пика не применяется для решения задач в пространстве.
Выдвинутая мной гипотеза подтвердилась. Я пришла к выводу, что тема, которая меня заинтересовала, достаточно многогранна, задачи на клетчатой бумаге многообразны, методы и приёмы их решения также разнообразны.
Приложение 1
Таблица №2. Сравнительный анализ времени, затраченного на решение задач.
| № | Геометрический способ
| По формуле Пика |
|
| достраиванием | по формуле |
|
| 1 | 5 минут |
| 2 мин |
| 2 | 2 минут | 24 секунд | 1 минут 15 секунд |
| 3 | 2 минут |
| 1 минут 20 секунд |
| 4 | 4 минут |
| 1 минут 30 секунд |
| 5 | 4 минут |
| 46 секунд |
| 6 |
| 25 секунд | 50 секунд |
| 7 |
| 4 минут | 3 минут |
| 8 |
| 4 минут | 3 минут |
| 9 |
| 5 минут | 2 минут |
| 10 |
| 5 минут | 2 минут |
| Всего | 34 минут 36 секунд | 17 минут 41 секунд |







 летчатая бумага (точнее — ее узлы), на которой мы часто предпочитаем рисовать и чертить, является одним из важнейших примеров точечной решетки на плоскости. Нарисуем на клетчатой бумаге какой-нибудь многоугольник (рисунок 1). Попробуем теперь рассчитать его площадь. Как это сделать? Наверное, проще всего разбить его на прямоугольные треугольники и трапецию, площади которых уже нетрудно вычислить и сложить полученные результаты.
летчатая бумага (точнее — ее узлы), на которой мы часто предпочитаем рисовать и чертить, является одним из важнейших примеров точечной решетки на плоскости. Нарисуем на клетчатой бумаге какой-нибудь многоугольник (рисунок 1). Попробуем теперь рассчитать его площадь. Как это сделать? Наверное, проще всего разбить его на прямоугольные треугольники и трапецию, площади которых уже нетрудно вычислить и сложить полученные результаты. спользованный способ несложен, но очень громоздок, кроме того он годится не для всяких многоугольников. Так следующий многоугольник нельзя разбить на прямоугольные треугольники, так как мы это проделали в предыдущем случае (рисунок 2). Можно, например, попробовать дополнить его до «хорошего», нужного нам, то есть до такого, площадь которого мы сможем вычислить описанным способом, потом из полученного числа вычесть площади добавленных частей.
спользованный способ несложен, но очень громоздок, кроме того он годится не для всяких многоугольников. Так следующий многоугольник нельзя разбить на прямоугольные треугольники, так как мы это проделали в предыдущем случае (рисунок 2). Можно, например, попробовать дополнить его до «хорошего», нужного нам, то есть до такого, площадь которого мы сможем вычислить описанным способом, потом из полученного числа вычесть площади добавленных частей.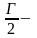 1, где
1, где 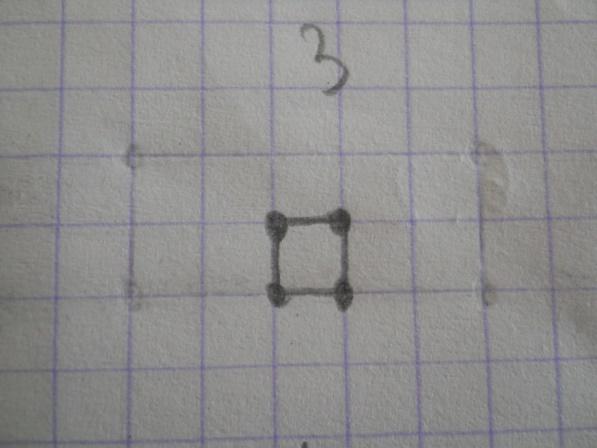 ез узлов внутри и на сторонах.
ез узлов внутри и на сторонах.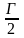 - 1.
- 1. оказательство: Рассмотрим произвольный прямоугольник со сторонами, параллельными осям координат. Его площадь – это произведение длины и ширины, т.е. S = 1*10 = 10. Для доказательства формулы посчитаем В = 0, Г = 22. Непосредственной подстановкой убеждаемся, что формула Пика верна.
оказательство: Рассмотрим произвольный прямоугольник со сторонами, параллельными осям координат. Его площадь – это произведение длины и ширины, т.е. S = 1*10 = 10. Для доказательства формулы посчитаем В = 0, Г = 22. Непосредственной подстановкой убеждаемся, что формула Пика верна. оказательство: Рассмотрим прямоугольный треугольник с катетами, параллельными осям координат.
оказательство: Рассмотрим прямоугольный треугольник с катетами, параллельными осям координат. 
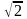 . Тогда катеты AB и AC данного треугольника будут равны
. Тогда катеты AB и AC данного треугольника будут равны 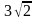 . Так как площадь прямоугольного треугольника равна половине произведения его катетов, то площадь данного треугольника будет равна 9. (Рис.1)
. Так как площадь прямоугольного треугольника равна половине произведения его катетов, то площадь данного треугольника будет равна 9. (Рис.1)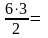 9. (Рис.2) Ответ: 9 .
9. (Рис.2) Ответ: 9 .

 айдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1.
айдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1. 

















