Государственное бюджетное профессиональное образовательное учреждение «Саткинский медицинский техникум»
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ
для обучающихся медицинских техникумов и колледжей
на тему: «Интегральное исчисление»
ЕН.01 Математика
Специальности 31.02.01 Лечебное дело 34.02.01 Сестринское дело
Сатка 2021
Учебно-методическое пособие для обучающихся медицинских техникумов и колледжей разработано в соответствии с требованиями Федерального Государственного образовательного стандарта по специальностей 31.02.01 Лечебное дело, 34.02.01 Сестринское дело
Организация–разработчик: ГБПОУ «Саткинский медицинский техникум»
Разработчик: Валеев Р.Ф. – преподаватель
Рассмотрена на заседании предметно-цикловой комиссии общих гуманитарных социально-экономических, общих профессиональных и естественнонаучных дисциплин.
Протокол №____от «____»_________________20___г. Председатель____________________Р.Ф. Дмитренко
Утверждена:
Зам.директора по УВР_________________А.Н.Гильмиярова
Оглавление
Пояснительная записка 4
Методические указания 4
Требования к результатам освоения дисциплины 5
1. Неопределенный интеграл. 8
2. Определенный интеграл. 16
Список использованных источников 25
Пояснительная записка
Цель преподавания математики в ССУЗе – ознакомить студентов с основами математического аппарата, необходимого для решения теоретических и практических задач; привить студентам умение самостоятельно изучать учебную литературу по математике и ее приложениям; развивать логическое мышление и формировать математическую культуру; выработать навыки математического исследования прикладных вопросов и умение перевести задачу на математический язык.
Данное пособие предназначено для студентов 1-го и 2-го курса отделений «Сестринское дело» и «Лечебное дело» для самостоятельной подготовки по темам «Неопределенный интеграл» и «Определенный интеграл».
Методические указания
Уважаемые студенты вам предлагается поэтапное изучение темы «Основы дифференциально-интегрального исчисления».
В каждом разделе предлагаются контрольные вопросы и задания, приводятся решения некоторых примеров и задач, а также приводятся задачи и упражнения, предназначенные для самостоятельной работы.
Выбор варианта производится соответственно номеру студента в списке группы.
Требования к результатам освоения дисциплины
В соответствии с государственным стандартом в области математики после изучения темы:
Вы должны иметь представление:
о математике как части мировой культуры и о месте математики в современной цивилизации, о способах описания на математическом языке явлений реального мира;
о математических понятиях как о важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;
об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей;
Вы должны уметь:
Вы должны знать:
значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы;
основные математические методы решения прикладных задач в области профессиональной деятельности;
основы интегрального и дифференциального исчисления.
Формируемые компетенции
ПК 1.2. Проводить диагностические исследования.
ПК 1.3. Участвовать в проведении профилактики инфекционных и неинфекционных заболеваний.
ПК 1.4. Проводить диагностику беременности.
ПК 1.5. Проводить диагностику комплексного состояния здоровья ребёнка.
ПК 1.7. Оформлять медицинскую документацию.
ПК 2.1. Представлять информацию в понятном для пациента виде, объяснять ему суть вмешательств.
ПК 2.2. Осуществлять лечебно-диагностические вмешательства, взаимодействуя с участниками лечебного процесса.
ПК 2.3. Сотрудничать с взаимодействующими организациями и службами.
ПК 2.4. Применять медикаментозные средства в соответствии с правилами их использования.
ПК 2.5. Осуществлять контроль состояния пациента.
ПК 2.8. Оформлять медицинскую документацию.
ПК 3.1. Оказывать доврачебную помощь при неотложных состояниях и травмах.
ПК 3.2. Определять тактику ведения пациента.
ПК 3.3. Взаимодействовать с членами профессиональной бригады и добровольными помощниками в условиях чрезвычайных ситуаций.
ПК 3.4. Проводить контроль эффективности проводимых мероприятий.
ПК 3.5. Осуществлять контроль состояния пациента.
ПК 3.7. Оформлять медицинскую документацию.
ПК 4.1. Организовывать диспансеризацию населения и участвовать в ее проведении.
ПК 4.2. Проводить санитарно-противоэпидемические мероприятия на закрепленном участке.
ПК 4.3. Проводить санитарно-гигиеническое просвещение населения.
ПК 4.4. Проводить диагностику групп здоровья.
ПК 4.5. Проводить иммунопрофилактику.
ПК 4.6. Проводить мероприятия по сохранению и укреплению здоровья различных возрастных групп населения.
ПК 4.9. Оформлять медицинскую документацию.
ПК 6.1. Рационально организовывать деятельность персонала с соблюдением психологических и этических аспектов работы в команде.
ПК 6.2. Планировать свою деятельность на фельдшерско-акушерском пункте, в здравпункте промышленных предприятий, детских дошкольных учреждениях, центрах общей врачебной (семейной) практики и анализировать ее эффективность.
ПК 6.3. Вести медицинскую документацию.
ПК 6.4. Организовывать и контролировать выполнение требований противо пожарной безопасности, техники безопасности и охраны труда на ФАПе, в здравпункте промышленных предприятий, детских дошкольных учреждениях, центрах офисе общей врачебной (семейной) практики.
Процесс изучения дисциплины направлен на формирование у обучающегося следующих общих компетенций (ОК), включающих в себя способность:
ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их выполнение и качество.
ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личного развития.
ОК 5.Использовать информационно-коммуникационные технологии в профессиональной деятельности.
ОК 12.Организовывать рабочее место с соблюдением требований охраны труда, производственной санитарии, инфекционной и противопожарной безопасности.
1. Неопределенный интеграл.
1.1 Понятие неопределенного интеграла.
В дифференциальном исчислении решается задача: по данной функции f(x) найти её производную (или дифференциал). Интегральное исчисление решает обратную задачу: найти функцию F(x), зная её производную F’=f(x) (или дифференциал). Искомую функцию F(x) называют первообразной функции f(x).
Функция F(x) называется первообразной функцииf(x) на интервале (a;b), если для любого 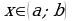 выполняется равенство
выполняется равенство
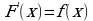 или
или 
Пример 1.
Для функции 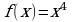 первообразной является функция
первообразной является функция 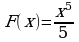
так как
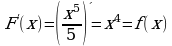
Очевидно, что первообразными будут также любые функции
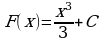
где С – постоянная, поскольку

Множество всех первообразных функций F(x)+C для f(x) называется неопределенным интегралом от функции f(x).
Таким образом по определению
 (1.1)
(1.1)
знак ∫называют знаком интеграла;
функцию f(x) называют подынтегральной функцией;
выражение f(x)dx называют подынтегральным выражением.
О перацию нахождения неопределенного интеграла называют интегрированием функции. Проинтегрировать функцию значит найти все её первообразные.
перацию нахождения неопределенного интеграла называют интегрированием функции. Проинтегрировать функцию значит найти все её первообразные.
Геометрически неопределенный интеграл представляет собой семейство «параллельных» кривых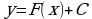 (см. рис. 1.3)
(см. рис. 1.3)
График каждой первообразной (кривой) называется интегральной кривой.
1.2 Свойства неопределенного интеграла.
1 Производная от неопределенного интеграла равна подынтегральной функции:

2 Дифференциал от неопределенного интеграла равен подынтегральному выражению:

3 Интеграл от дифференциала первообразной равен самой первообразной плюс произвольная постоянная:

4 Постоянный множитель можно выносить за знак интеграла:

5 Интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от слагаемых:

1.3 Основные формулы интегрирования (табличные интегралы).
1  ; (1.2)
; (1.2)
2  ; (1.3)
; (1.3)
3 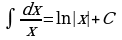 ; (1.4)
; (1.4)
4  ; (1.5)
; (1.5)
5 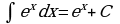 ; (1.6)
; (1.6)
6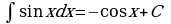 ; (1.7)
; (1.7)
7  ; (1.8)
; (1.8)
8  ; (1.9)
; (1.9)
9  ; (1.10)
; (1.10)
10  ; (1.11)
; (1.11)
11  . (1.12)
. (1.12)
1.4 Метод непосредственного интегрирования.
Метод интегрирования, при котором данный интеграл путем тождественных преобразований и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.
При сведении данного интеграла к табличному часто используются следующие преобразования дифференциала (операция «подведения под знак дифференциала»);
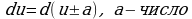

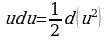


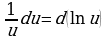
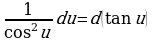
Пример 1.
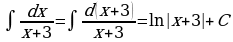
Пример 2.

1.5 Интегрирование методом замены переменной
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (т.е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует.
Допустим требуется вычислить интеграл  . Сделаем подстановку
. Сделаем подстановку  , где
, где  - функция имеющая непрерывную производную.
- функция имеющая непрерывную производную.
Тогда  и на основе свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой.
и на основе свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой.

Данная формула называется формулой интегрирования методом замены переменных в неопределенном интеграле. После нахождения интеграла правой части этого выражения следует перейти от новой переменной интегрирования t назад к переменной x.
Иногда целесообразно подбирать подстановку в виде  , тогда
, тогда

Вопросы для самоконтроля
1. Какое действие называется интегрированием?
2. Какая функция называется подынтегральной?
3. Перечислите основные свойства неопределенного интеграла.
4. Перечислите основные методы интегрирования.
5. Чем отличаются друг от друга различные первообразные функции для данной функции f(x)?
Задания для самостоятельной работы
Найдите следующие интегралы.
1.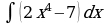
Используя свойство (5) раскроем скобки.
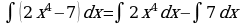
Согласно свойству (4) постоянный множитель можно вынести за знак интеграла

По формулам (3.2) и (3.3), полагая, что n=4, найдем интеграл.

гдеС=С1+С2.
2.
Решение:

3.
Решение

4.
Данный интеграл находится методом замены переменной.

5.
Решение

6.
Решение

7.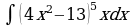
Решение

8.Найдите следующие интегралы.
| Вариант 1. а) ; ; б) ; ; в)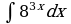 . . | Вариант 2. а) ; ; б) ; ; в) . . |
| Вариант 3. а)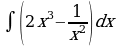 ; ; б)  ; ; в)  . . | Вариант 4. а) ; ; б) ; ; в)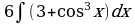 . . |
| Вариант 5. а) ; ; б)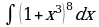 ; ; в)  . . | Вариант 6. а) ; ; б) ; ; в) . . |
| Вариант 7. а)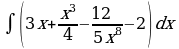 ; ; б)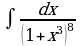 ; ; в)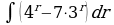 . . | Вариант 8. а) ; ; б) ; ; в) . . |
| Вариант 9. а) ; ; б) ; ; в) . . | Вариант 10. а)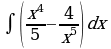 ; ; б) ; ; в) . . |
| Вариант 11. а) ; ; б) ; ; в)  . . | Вариант 12. а) ; ; б) ; ; в) . . |
| Вариант 13. а) ; ; б) ; ; в) . . | Вариант 14. а) ; ; б) ; ; в) . . |
| Вариант 15. а) ; ; б)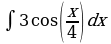 ; ; в) . . | Вариант 16. а)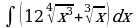 ; ; б) ; ; в) . . |
| Вариант 17. а)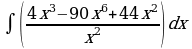 ; ; б) ; ; в) . . | Вариант 18. а)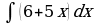 ; ; б) ; ; в) . . |
| Вариант 19. а) ; ; б) ; ; в) . . | Вариант 20. а)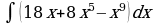 ; ; б) ; ; в) . . |
| Вариант 21. а)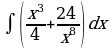 ; ; б) ; ; в)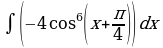 . . | Вариант 22. а) ; ; б) ; ; в)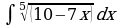 . . |
| Вариант 23. а) ; ; б)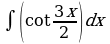 ; ; в) . . | Вариант 24. а) ; ; б)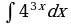 ; ; в) . . |
| Вариант 25. а)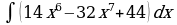 ; ; б)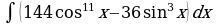 ; ; в) . . | Вариант 26. а)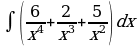 ; ; б) ; ; в)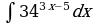 . . |
| Вариант 27. а) ; ; б)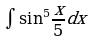 ; ; в) . . | Вариант 28. а) ; ; б) ; ; в) . . |
| Вариант 29. а) ; ; б) ; ; в) . . | Вариант 30. а) ; ; б)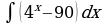 ; ; в) . . |
| Вариант 31. а) ; ; б) ; ; в)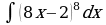 . . | Вариант 32. а)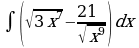 ; ; б)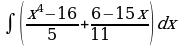 ; ; в)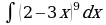 . . |
| Вариант 33. а) ; ; б) ; ; в) . . | Вариант 34. а) ; ; б) ; ; в) . . |
| Вариант 35. а) ; ; б) ; ; в) . . | Вариант 36. а) ; ; б) ; ; в) . . |
| Вариант 37. а) ; ; б) ; ; в) . . | Вариант 38. а) ; ; б) ; ; в) . . |
| Вариант 39. а) ; ; б)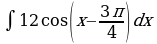 ; ; в) . . | Вариант 40. а)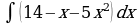 ; ; б)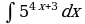 ; ; в) . . |
2. Определенный интеграл.
2.1 Определенный интеграл как предел интегральной суммы.
Пусть функция  определена на отрезке
определена на отрезке  . Выполним следующие действия.
. Выполним следующие действия.
С помощью точек x0=a, x1, x2,…xn=b (x0x1x2xn) разобьем на n частичных отрезков 

В каждом частичном отрезке  выберем произвольную точку
выберем произвольную точку  и вычислим значение функции в ней, т. е. величину
и вычислим значение функции в ней, т. е. величину 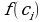 .
.
Умножим найденное значение функции 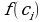 на длину
на длину  соответствующего частичного отрезка:
соответствующего частичного отрезка:  .
.
Составим сумму всех таких произведений:
 (2.1)
(2.1)
Сумма вида (4.1) называется интегральной суммой функции  на отрезке
на отрезке  .
.
Обозначим через λ длину наибольшего частичного отрезка:  .
.
Найдем предел интегральной суммы (2.1), когда  так, что
так, что  .
.
Если при этом интегральная сумма Sn имеет предел I, который не зависит ни от способа разбиения отрезка на частичные отрезки, ни от выбора точек в них, то число I называется определенным интегралом от функции  на отрезке
на отрезке  .
.
 (2.2)
(2.2)
4.2 Геометрический смысл определенного интеграла.
Пусть на отрезке  задана непрерывная функция
задана непрерывная функция  . Фигура, ограниченная сверху графиком функции
. Фигура, ограниченная сверху графиком функции  , снизу осью Ox, сбоку – прямыми x=a и x=b, называется криволинейной трапецией. Требуется найти её площадь.
, снизу осью Ox, сбоку – прямыми x=a и x=b, называется криволинейной трапецией. Требуется найти её площадь.

Рис. 2.2
Для этого отрезок  точками x0=a, x1, x2,…xn=b (x0x1x2xn) разобьем на nчастичных отрезков
точками x0=a, x1, x2,…xn=b (x0x1x2xn) разобьем на nчастичных отрезков  . В каждом частичном отрезке
. В каждом частичном отрезке  возьмем произвольную точку сi и вычислим значение функции в ней, т.е.
возьмем произвольную точку сi и вычислим значение функции в ней, т.е. 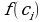 .
.
Умножим значение функции 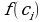 на длину
на длину  , соответствующего частичного отрезка. Произведение
, соответствующего частичного отрезка. Произведение  равно площади прямоугольника с основанием
равно площади прямоугольника с основанием  и высотой
и высотой 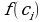 . Сумма всех таких произведений
. Сумма всех таких произведений

равна площади ступенчатой фигуры и приближенно равна площади S криволинейной трапеции:

С уменьшением всех величин  , точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличиваются. Поэтому за точное значение площади S криволинейной трапеции принимается предел S, к которому стремится площадь ступенчатой фигуры Sст, когда n неограниченно возрастает так, что:
, точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличиваются. Поэтому за точное значение площади S криволинейной трапеции принимается предел S, к которому стремится площадь ступенчатой фигуры Sст, когда n неограниченно возрастает так, что:
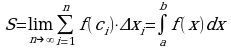 (2.3)
(2.3)
Итак, определенный интеграл от функции численно равен площади криволинейной трапеции.
В этом и состоит геометрический смысл определенного интеграла.
2.3 Свойства определенного интеграла.
Если верхний и нижний пределы интегрирования равны, то интеграл равен нулю:

При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:

Если функция  интегрируема на отрезке
интегрируема на отрезке  и acb, то
и acb, то

«Теорема о среднем». Если функция  непрерывна на отрезке
непрерывна на отрезке  , то существует точка
, то существует точка 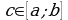 такая, что:
такая, что:

Оценка интеграла. Если m и M– соответственно наименьшее и наибольшее значения функции  на отрезке
на отрезке  , то
, то
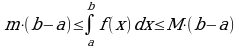
Неравенство между непрерывными функциями на отрезке  можно интегрировать. Так, если
можно интегрировать. Так, если 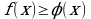 при
при , то
, то

Постоянный множитель можно выносить за знак интеграла:
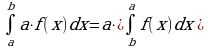
Интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от слагаемых:

2.4 Формула Ньютона-Лейбница.
Формула Ньютона-Лейбница дает правило вычисления определенного интеграла: значение определенного интеграла на отрезке  от непрерывной функции
от непрерывной функции  равно разности значений любой ее первообразной, вычисленной при x=b и x=a.
равно разности значений любой ее первообразной, вычисленной при x=b и x=a.

Здесь a и b – соответственно нижний и верхний предел интегрирования.
Общность обозначения определенного и неопределенного интегралов подчеркивает тесную связь между ними, но это разные понятия по смыслу: определенный интеграл – это число, а неопределенный интеграл – совокупность первообразных функций. Связь между определенным и неопределенным интегралом выражается методами интегрирования.
Пример 1.
Вычислите 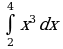
Решение

2.5 Интегрирование методом замены переменной.
Этот метод, как и в случае неопределенного интеграла, позволяет упростить вычисления, т.е. привести подынтегральное выражение к соответствующей табличной форме. Применение замены переменной в определенном интеграле базируется на следующей теореме.
Теорема. Если функция  непрерывна на отрезке
непрерывна на отрезке  , а функция
, а функция  непрерывна дифференцируема на отрезке
непрерывна дифференцируема на отрезке 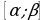 , причем
, причем  и
и  , то справедлива формула
, то справедлива формула

Вопросы для самоконтроля
1. Как найти площадь криволинейной трапеции?
2. Перечислите свойства определенного интеграла.
3.В чем заключается геометрический смысл определенного интеграла?
4. Назовите формулу Ньютона-Лейбница.
Задания для самостоятельной работы
1.Вычислите 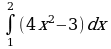
Решение
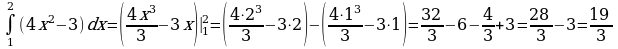
2.Вычислите 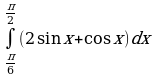
Решение

3.Вычислите интеграл 
Решение

4.Вычислите интеграл 
Решение

5.Вычислите интеграл 
Решение

6. Вычислите определенный интеграл
| Вариант 1. а) ; ; б) ; ; в) . . | Вариант 2. а)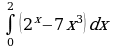 ; ; б) ; ; в) . . |
| Вариант 3. а) ; ; б) ; ; в) . . | Вариант 4. а) ; ; б)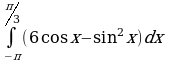 ; ; в) . . |
| Вариант 5. а) ; ; б)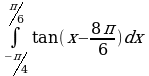 ; ; в)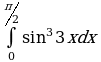 . . | Вариант 6. а) ; ; б)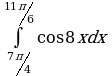 ; ; в) . . |
| Вариант 7. а)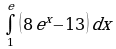 ; ; б) ; ; в) . . | Вариант 8. а)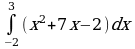 ; ; б) ; ; в) . . |
| Вариант 9. а)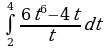 ; ; б) ; ; в)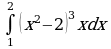 . . | Вариант 10. а) ; ; б) ; ; в)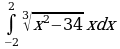 . . |
| Вариант 11. а)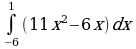 ; ; б) ; ; в) . . | Вариант 12. а) ; ; б) ; ; в)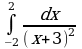 . . |
| Вариант 13. а) ; ; б) ; ; в) . . | Вариант 14. а) ; ; б) ; ; в)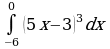 . . |
| Вариант 15. а)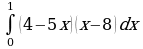 ; ; б) ; ; в)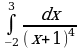 . . | Вариант 16. а) ; ; б) ; ; в) . . |
| Вариант 17. а) ; ; б) ; ; в) . . | Вариант 18. а) ; ; б) ; ; в) . . |
| Вариант 19. а) ; ; б) ; ; в) . . | Вариант 20. а) ; ; б) ; ; в) . . |
| Вариант 21. а) ; ; б)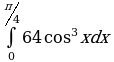 ; ; в) . . | Вариант 22. а) ; ; б)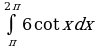 ; ; в) . . |
| Вариант 23. а ; ; б) ; ; в) . . | Вариант 24. а) ; ; б) ; ; в) . . |
| Вариант 25. а)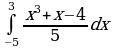 ; ; б) ; ; в) . . | Вариант 26. а) ; ; б) ; ; в)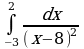 . . |
| Вариант 27. а) ; ; б) ; ; в) . . | Вариант 28. а) ; ; б) ; ; в)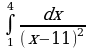 . . |
| Вариант 29. а)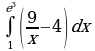 ; ; б) ; ; в) . . | Вариант 30. а) ; ; б)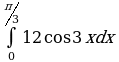 ; ; в)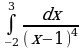 . . |
| Вариант 31. а) ; ; б) ; ; в)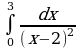 . . | Вариант 32. а) ; ; б) ; ; в)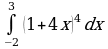 . . |
| Вариант 33. а) ; ; б)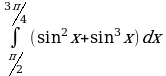 ; ; в) . . | Вариант 34. а)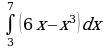 ; ; б)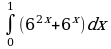 ; ; в)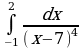 . . |
| Вариант 35. а) ; ; б)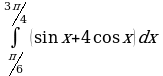 ; ; в) . . | Вариант 36. а) ; ; б) ; ; в) . . |
| Вариант 37. а)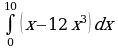 ; ; б)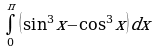 ; ; в)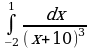 . . | Вариант 38. а) ; ; б) ; ; в) . . |
| Вариант 39. а) ; ; б) ; ; в)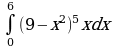 . . | Вариант 40. а)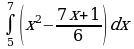 ; ; б) ; ; в) . . |
Список использованных источников
Основные источники:
Гилярова М. Г. Математика для мед. колледжей: учебник. -Изд. 5-е.- Ростов н/Д: Феникс, 2016.
Дополнительные источники:
Омельченко, В. П. Математика : учебник / Омельченко В. П. - Москва : ГЭОТАР-Медиа, 2020. - 304 с. - ISBN 978-5-9704-5369-8. - Текст : электронный // URL : http://www.medcollegelib.ru/book/ISBN9785970453698.html






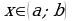 выполняется равенство
выполняется равенство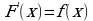 или
или 
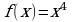 первообразной является функция
первообразной является функция 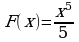
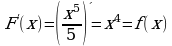
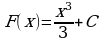

 (1.1)
(1.1) перацию нахождения неопределенного интеграла называют интегрированием функции. Проинтегрировать функцию значит найти все её первообразные.
перацию нахождения неопределенного интеграла называют интегрированием функции. Проинтегрировать функцию значит найти все её первообразные.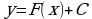 (см. рис. 1.3)
(см. рис. 1.3)




 ; (1.2)
; (1.2) ; (1.3)
; (1.3)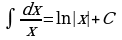 ; (1.4)
; (1.4) ; (1.5)
; (1.5)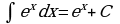 ; (1.6)
; (1.6)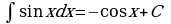 ; (1.7)
; (1.7) ; (1.8)
; (1.8) ; (1.9)
; (1.9) ; (1.10)
; (1.10) ; (1.11)
; (1.11) . (1.12)
. (1.12)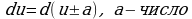

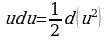


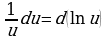
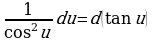
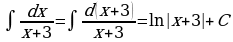

 . Сделаем подстановку
. Сделаем подстановку  , где
, где  - функция имеющая непрерывную производную.
- функция имеющая непрерывную производную. и на основе свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой.
и на основе свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой.
 , тогда
, тогда
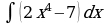
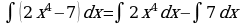












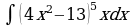

 ;
; ;
;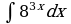 .
. ;
; ;
; .
.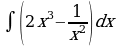 ;
; ;
; .
. ;
; ;
;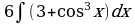 .
. ;
;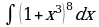 ;
; .
. ;
; ;
; .
.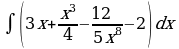 ;
;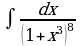 ;
;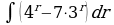 .
. ;
; ;
; .
. ;
; ;
; .
.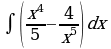 ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
;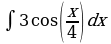 ;
; .
.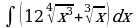 ;
; ;
; .
.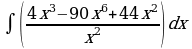 ;
; ;
; .
.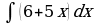 ;
; ;
; .
. ;
; ;
; .
.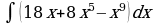 ;
; ;
; .
.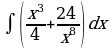 ;
; ;
;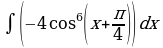 .
. ;
; ;
;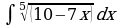 .
. ;
;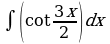 ;
; .
. ;
;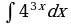 ;
; .
.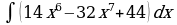 ;
;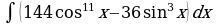 ;
; .
.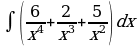 ;
; ;
;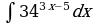 .
.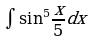 ;
; .
. ;
; .
. ;
; ;
; .
. ;
;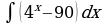 ;
; .
. ;
; ;
;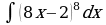 .
.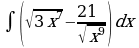 ;
;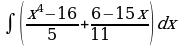 ;
;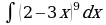 .
. ;
; ;
; .
. ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
;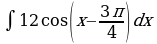 ;
; .
.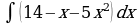 ;
;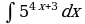 ;
; .
. определена на отрезке
определена на отрезке  . Выполним следующие действия.
. Выполним следующие действия. 

 выберем произвольную точку
выберем произвольную точку  и вычислим значение функции в ней, т. е. величину
и вычислим значение функции в ней, т. е. величину 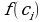 .
. соответствующего частичного отрезка:
соответствующего частичного отрезка:  .
. (2.1)
(2.1) .
. .
. так, что
так, что  .
. (2.2)
(2.2)
 возьмем произвольную точку сi и вычислим значение функции в ней, т.е.
возьмем произвольную точку сi и вычислим значение функции в ней, т.е.  и высотой
и высотой 

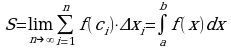 (2.3)
(2.3)

 интегрируема на отрезке
интегрируема на отрезке 
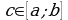 такая, что:
такая, что:
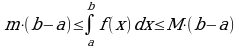
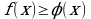 при
при , то
, то 
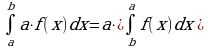


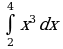

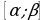 , причем
, причем  и
и  , то справедлива формула
, то справедлива формула
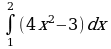
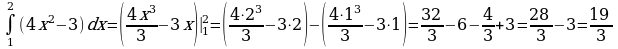
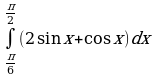







 ;
; ;
; .
.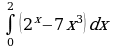 ;
; ;
; .
. ;
; ;
; .
. ;
;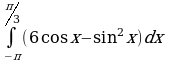 ;
; .
. ;
;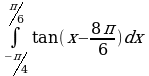 ;
;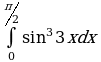 .
. ;
;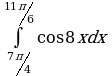 ;
; .
.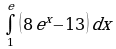 ;
; ;
; .
.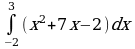 ;
; ;
; .
.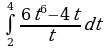 ;
; ;
;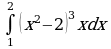 .
. ;
; ;
;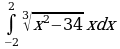 .
.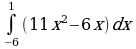 ;
; ;
; .
. ;
; ;
;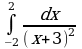 .
. ;
; ;
; .
. ;
; ;
;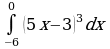 .
.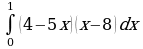 ;
; ;
;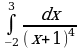 .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
;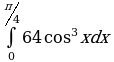 ;
; .
. ;
;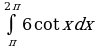 ;
; .
. ;
; ;
; .
. ;
; ;
; .
.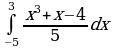 ;
; ;
; .
. ;
; ;
;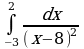 .
. ;
; ;
; .
. ;
; ;
;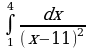 .
.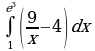 ;
; ;
; .
. ;
;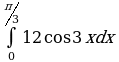 ;
;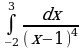 .
. ;
; ;
;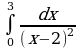 .
. ;
; ;
;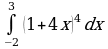 .
. ;
;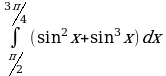 ;
; .
.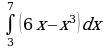 ;
;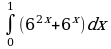 ;
;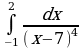 .
. ;
;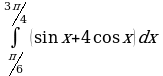 ;
; .
. ;
; ;
; .
.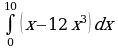 ;
;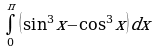 ;
;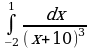 .
. ;
; ;
; .
. ;
; ;
;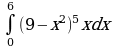 .
.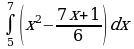 ;
; ;
; .
.









