|
|
| Учебное пособие для учителей математики и учащихся 9 классов по теме: «Решение заданий по геометрии повышенного уровня сложности (КИМ-ОГЭ №23)» |
| Составила: учитель математики МОБУ «СОШ с. Веденка» Поздышева Н.С. |
Критерии оценки выполнения задания 23
| Баллы | Критерии оценки выполнения задания |
| 2 | Ход решения верный, все его шаги выполнены правильно, получен верный ответ |
| 1 | Ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка |
| 0 | Другие случаи, не соответствующие указанным выше критериям |
| 2 | Максимальный балл |
Можно привести различные классификации задач по геометрии. В данном пособии разобьем их по трем группам в зависимости от набора понятий и теорем, используемых при решении задач.
-
Базовые понятия и свойства фигур
Задача 1.(4.2.43-4.2.44)
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN = 11, AC = 44, NC = 18.
Р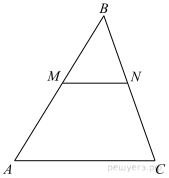 ешение:
ешение:
Докажем, что треугольники АВС и BMN подобны.
BAC=BMN как соответственные углы при параллельных прямых MN и AC и секущей АВ. Значит, 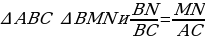 .
.
Обозначим BN=x, тогда BC= x+18. Получаем уравнение 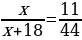 .
.
Откуда
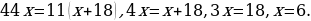
Следовательно, BN=6.
Ответ: 6.
Задача 2.(4.2.45-4.2.46, варианты 16-20)
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 11, DC = 22, AC = 27.
Решение:
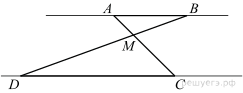
Углы DCM и BAM равны как накрест лежащие, углы DMC и BMA равны как вертикальные, следовательно, треугольники DMC и BMA подобны по двум углам. Значит,
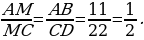
Следовательно, 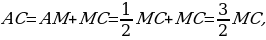 откуда
откуда
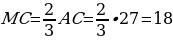 .
.
Ответ: 18.
Задача 3. (4.2.47-4.2.48)
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD = 45, BC = 20, CF : DF = 4 : 1.
Решение 1 способ.
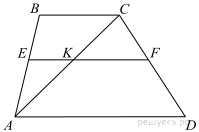
Проведём построения и введём обозначения, как показано на рисунке. Рассмотрим треугольники KFC и ACD угол C — общий, углы CAD и CKF равны друг другу как соответственные углы при параллельных прямых, следовательно,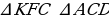 . Откуда
. Откуда 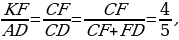 поэтому
поэтому
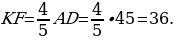
Аналогично, из подобных треугольников EKA и ABC получаем, что
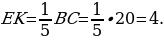 Таким образом, EF=EK+KF=4+36=40.
Таким образом, EF=EK+KF=4+36=40.
Ответ: 40.


Сс
В
2 способ. 




E
K
F




D
N
А
Проведем прямую СN параллельно АВ, она пересекает отрезки EF и AD в точках K и N соответственно.
Четырехугольник BCNА – параллелограмм, потому что его стороны попарно параллельны. Тогда ВС=АN=20 (противоположные стороны параллелограмма равны). Аналогично, BC=ЕK=20. Найдем длину отрезка ND.
ND=AD-AN=45-20=25.
Рассмотрим треугольники CEF и CND. Угол C у них общий, CND=CKF как соответственные углы при параллельных прямых EF и AD и секущей CN, значит треугольники подобны по двум углам.
Следовательно, 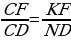 . Обозначим CF=4x, DF=x, тогда CD=x+4x=5x.
. Обозначим CF=4x, DF=x, тогда CD=x+4x=5x.
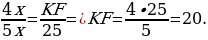
Тогда EF=EK+KF=20+20=40.
Ответ: 40.
Задача 4.
Биссектрисы углов А и D параллелограмма ABCD пересекаются в точке Н, лежащей на стороне СВ. Найдите ВС, если АВ=40.
Решение:
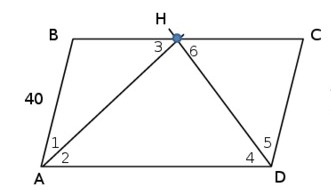
АН – биссектриса угла BAD, следовательно, AD и ВС и секущей АН.
Получаем
Аналогично DH – биссектриса угла ADC, следовательно, AD и ВС и секущей DH. Получаем DНC – равнобедренный и CD=CН.
AB=BH, HC=CD. Противоположные стороны параллелограмма равны, так AB=CD=40 и BC=AD, следовательно, BH=HC=AB=40, и тогда BC=40·2=80.
Ответ: 80.
Задача 5. (4.2.57-4.2.58)
Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К. Найдите периметр параллелограмма, если ВК=6, СК=10.
Решение:
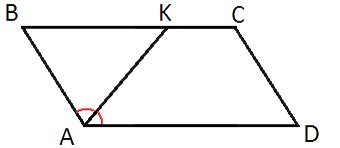
Обозначим BAK=KAD=BKA=
АК – биссектриса угла BAD, следовательно, AD и BC и секущей АК.
Получаем
Противоположные стороны параллелограмма равны, так AD=ВС=ВК+КС=6+10=16, АВ=CD=6.
Периметр параллелограмма ABCD равен Р=2(АВ+ВС)=2·(6+16)=44.
Ответ: 44.
-
Прямоугольный треугольник и его свойства
Задача 6. (4.2.49-4.2.50)
Катеты прямоугольного треугольника равны 15 и 36. Найдите высоту, проведенную к гипотенузе.
Решение:
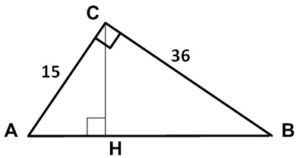
Рассмотрим прямоугольный треугольник АВС с прямым углом С и катетами АС=15, ВС=36. Проведем высоту СН к гипотенузе АВ.
Найдем гипотенузу треугольника по теореме Пифагора.
АВ2=АС2+ВС2=152+362=225+1296=1521, АВ=39.
Площадь прямоугольного треугольника, с одной стороны, равна половине произведения катетов, с другой стороны, она равна половине произведения основания (гипотенузы) на высоту, проведенную к основанию (гипотенузе).
 , тогда
, тогда 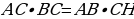 .
.
15·36=39·СН. Тогда СН=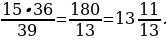
Ответ: 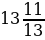 .
.
Задача 7. (4.2.51-4.2.52)
Точка Н является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH = 10, AC = 40.
Решение:
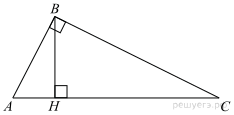
Способ 1.
Рассмотрим треугольник АВН и ВНС. 0-C=A, AHB=BHC=900, значит, треугольники подобны по двум углам. В подобных треугольниках против равных углов лежат пропорциональные стороны.
Запишем пропорцию 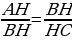 , НС=АС-АН=40-10=30.
, НС=АС-АН=40-10=30.
Тогда ВН2=АН·НС=10·30=300.
Найдем гипотенузу АВ треугольника АВН по теореме Пифагора. АВ2=АН2+НВ2=102+300=400. АВ=20.
Ответ: 20.
Способ 2.
Рассмотрим треугольники АВС и АВН. Угол А у них общий, AHB=ABC=900, значит, треугольники подобны по двум углам. В подобных треугольниках против равных углов лежат пропорциональные стороны.
Запишем пропорцию 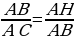 , тогда АВ2=АС·АН=40·10=400, АВ=20.
, тогда АВ2=АС·АН=40·10=400, АВ=20.
Ответ: 20.
Задача 8. (4.2.53-4.2.54, варианты 21-25)
Высота АН ромба ABCD делит сторону CD на отрезки DH=16 и CH=4. Найдите высоту ромба.
Решение:
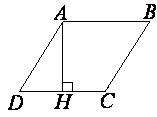
Поскольку ABCD – ромб, AD=DC=DH+HC=16+4=20.
Треугольник DAH прямоугольный, находим катет по теореме Пифагора:
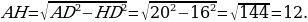
Ответ: 12.
Задача 9. (4.2.55-4.2.56)
Найдите боковую сторону АВ трапеции ABCD, если углы АВС и BCD равны соответственно 450 и 1500, а CD=26.
Решение:
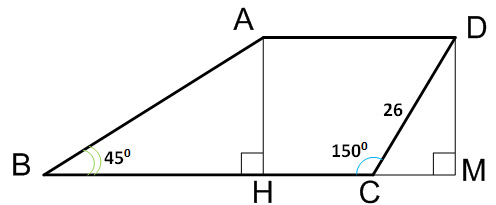
В трапеции ABCD проведем высоты АН и DM.
Рассмотрим прямоугольный треугольник ∆DMC.
Угол ∠DСM и ∠ВСD – смежные углы, тогда
∠DСM + ∠ВСD = 1800, ∠DСM = 1800 – ∠ВСD = 1800 – 1500 = 300. 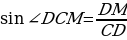 .
.
DM = DC·sin∠DСM, DM = 26·sin300.
(или треугольник ∆DMC – прямоугольный, ∠DСM = 300. DM – катет, лежащий против угла в 300, следовательно, DM равен половине гипотенузы DС, т. е. 13) 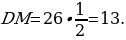
Рассмотрим прямоугольный треугольник ∆АВН: АН = DM, ∠АВН = 450.
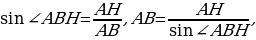
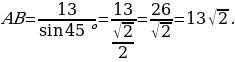
Получим, боковая сторона 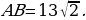
Ответ: 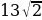 .
.
Задача 10. (4.2.59-4.2.60, варианты 7-8, 11-15)
Биссектрисы углов А и В при боковой стороне АВ трапеции ABCD пересекаются в точке F. Найдите АВ, если AF=12, BF=5.
Решение:
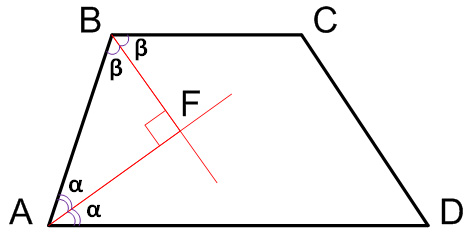
Основания трапеции параллельны, поэтому ∠BAD+∠ABC=1800.
BF и AF – биссектрисы углов ∠АВС и ∠BAD, поэтому
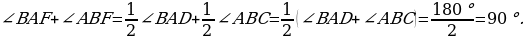
Следовательно, ∠BFA=900 и треугольник ABF прямоугольный. По теореме Пифагора гипотенуза равна 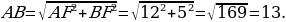
Ответ: 13.
-
Окружность и ее свойства
Задача 11.
Отрезки АВ и CD являются хордами окружности. Найдите длину хорды CD, если АВ = 24, а расстояние от центра окружности до хорд АВ и CD равны соответственно 16 и 12.
Решение:
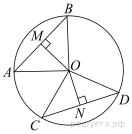
Пусть O — центр окружности, OM = 16 и ON = 12 — перпендикуляры к хордам AB и CD соответственно. Треугольники АОВ и COD равнобедренные поскольку ОА=ОВ=ОС=OD=r. Тогда ОМ и ON медианы, а значит АМ=МВ=12 и CN=ND.
По теореме Пифагора для прямоугольного треугольника OMB имеем: 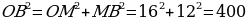 , откуда ОВ = 20.
, откуда ОВ = 20.
В прямоугольном треугольнике СON гипотенуза СО=ОВ=20, откуда по теореме Пифагора 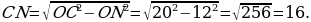
Получаем, что CD=2CN=32.
Ответ: 32.
Задача 12. (4.2.61-4.2.62, вариант 5)
Отрезки АВ и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если АВ = 30, CD=40, а расстояние от центра окружности до хорды АВ равно 20.
Решение:

Пусть O — центр окружности, OM =20 и ON — перпендикуляры к хордам AB и CD соответственно. Треугольники АОВ и COD равнобедренные поскольку ОА=ОВ=ОС=OD=r. Тогда ОМ и ON медианы, а значит АМ=МВ=15 и CN=ND=20.
По теореме Пифагора для прямоугольного треугольника OMB имеем:  , откуда ОВ = 25.
, откуда ОВ = 25.
В прямоугольном треугольнике СON гипотенуза СО=ОВ=25, откуда по теореме Пифагора 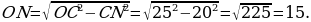
Получаем, что ОN=15.
Ответ: 15.
Задача 13. (4.2.63)
В окружности проведены две взаимно перпендикулярные хорды. Каждая из них делится другой хордой на отрезки, равные 4 и 6. Найдите расстояние от центра окружности до каждой хорды.
Решение:
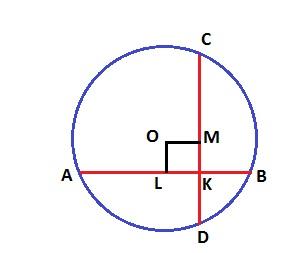
Опустим перпендикуляры ОМ и OL на хорды из центра окружности О. Четырехугольник OLKM – прямоугольник. ОМ делит хорду CD пополам (Перпендикуляр, проведенный из центра окружности к хорде, делит эту хорду и стягиваемые ею дуги пополам.)
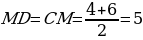 , MK=MD-KD=5-4=1.
, MK=MD-KD=5-4=1.
Аналогично, LK=1. Значит четырехугольник OLKM – квадрат.
OL=OM=1 – расстояние от центра окружности до хорд.
Ответ: 1
Задача 14. (4.2.64)
В окружности проведены две взаимно перпендикулярные хорды. Одна из хорд удалена от центра на расстоянии 6, а другая – на расстоянии 8. На каком расстоянии от центра окружности находится точка пересечения хорд?
Решение:

Опустим перпендикуляры ОМ и OL на хорды из центра окружности О. Четырехугольник OLKM – прямоугольник. ОМ=8, OL=6 по условию.
Искомое расстояние ОК от центра окружности до точки пересечения хорд – диагональ прямоугольника OLKM.
Треугольник ОМК – прямоугольный, тогда по теореме Пифагора находим
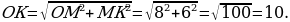
Ответ: 10.
Задача 15.
В треугольнике АВС известно, что ∠В=380 и дуга AB окружности, описанной около треугольника АВС, равна 1640. Найдите радиус этой окружности, если сторона ВС равна 36.
Решение:
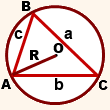
Обозначим R радиус описанной окружности треугольника АВС. По теореме синусов для треугольника АВС
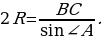
Угол ВСА вписанный, опирается на дугу АВ, следовательно, ∠АСВ=1640:2=820.
Из треугольника АВС
∠А=1800 - ∠В - ∠С=1800-380-820=600,
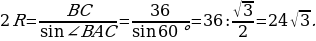
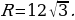
Ответ: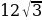 .
.
Задача 16. (4.2.65-4.2.66)
Углы В и С треугольника АВС равны соответственно 660 и 840. Найдите ВС, если радиус окружности, описанной около треугольника АВС, равен 15.
Решение:
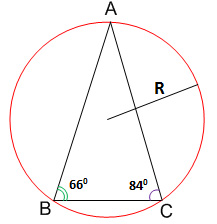
Воспользуемся формулой для радиуса описанной около треугольника окружности
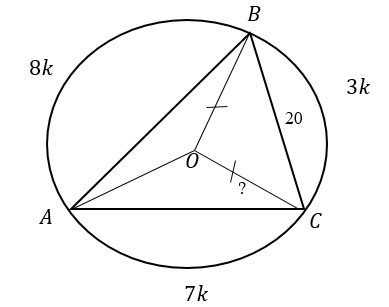
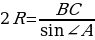 .
.
Выразим из нее ВС:
BC = 2R·sin∠A.
Сумма углов треугольника равна 1800: ∠А + ∠В + ∠С = 1800.
Тогда ∠А = 1800 – (∠В + ∠С) = 1800 – (660 + 840) = 300,
BC = 2·15·sin300 = 2·15·(1/2) = 15
Ответ: 15.
Задача 17. ( 4.2.67-4.2.68, варианты 9-10)
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:7:8. Найдите радиус окружности, если меньшая из сторон равна 20.
Решение:
Вычислим величины дуг, на которые делят окружность вершины треугольника. Пусть х – одна часть, тогда дуга ВС=3х, дуга АС=7х, дуга АВ=8х.
Градусная мера дуги всей окружности 3600. Значит:
3х+7х+8х=3600,
18х=3600,
х=3600:18,
х=200.
Следовательно, дуга ВС = 3∙200=600.
Угол ∠ВОС – центральный, опирается на дугу ВС, значит ∠ВОС=600.
Треугольник ВОС – равнобедренный, т.к.ОВ=ОС (радиусы), по свойству углов в равнобедренном треугольнике ∠ОВС=∠ОСВ=(1800-∠ВОС):2=(1800-600):2=600.
Следовательно, ΔВОС – равносторонний и ОС=ОВ=ВС=20.
Ответ: 20.
Задача 18. (4.2.69-4.2.70, варианты 3-4)
Точка Н является основанием высоты ВН, проведенной из вершины прямого угла В прямоугольного треугольника АВС. Окружность с диаметром ВН пересекает стороны АВ и ВС в точках Р и К соответственно. Найдите ВН, если РК = 14.
Решение:
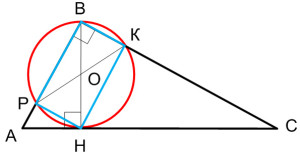
Рассмотрим четырехугольник BKHP, вписанный в окружность.
В любом вписанном четырехугольнике сумма противоположных углов равна 1800.
Угол ∠PBK = 900, следовательно, угол ∠КНР = 1800 – ∠PBK = 900.
Угол ∠BPН = 900, так как это вписанный в окружность угол, опирающийся на полуокружность, следовательно, угол ∠ВКН = 1800 – ∠BPН = 900.
Получаем, ∠PBK = ∠ВКН = ∠КНР = ∠BPН = 900, следовательно, четырехугольник BKHP – прямоугольник.
По свойству прямоугольника (диагонали прямоугольника равны): ВН = РК = 14.
Ответ:14.
Задача 19. (4.2.71-4.2.72)
Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В. Найдите диаметр окружности, АВ = 2, АС = 8.
Решение:
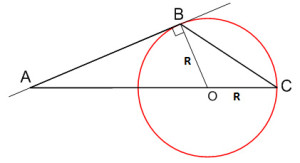
Диаметр окружности равен двум радиусам, т. е. D = 2R.
Окружность с центром на стороне АС треугольника АВС проходит через вершину С, тогда ОС – радиус окружности, т. е. ОС = R.
Окружность касается прямой АВ в точке В, тогда АВ перпендикулярна к радиусу окружности ВО, проведенному в точку касания. Получим треугольник ∆АВО – прямоугольный, АО – гипотенуза, АВ и ВО – катеты. Найдем АО по теореме Пифагора:
АО2 = АВ2 + ВО2,
АО2 = 22 + R2,
АО2 = 4 + R2,
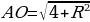 .
.
Сторона АС=АО+ОС, подставим соответствующие данные в это равенство, получим
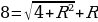 ,
,
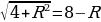 ,
,
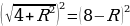 ,
,
4 + R2 = 64 – 16R + R2
16R = 60
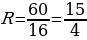 ,
,
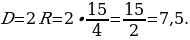
Ответ: 7,5.
Задача 20. (4.2.73-4.2.74, варианты 1-2, 26-30)
Окружность пересекает стороны АВ и АС треугольника АВС в точках К и Р соответственно и проходит через вершины В и С. Найдите длину отрезка КР, если АР=9, а сторона ВС в 3 раза меньше стороны АВ.
Решение:

Четырехугольник ВКРС вписан в окружность, значит, ∠KВС + ∠КРС=1800. Углы АРК и КРС смежные, значит, их сумма также равна 1800. Получаем, что ∠KВС = ∠АРК.
В треугольнике АВС и АРК угол А – общий, ∠KВС = ∠АРК, следовательно, эти треугольники подобны. Значит, 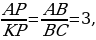 откуда получаем, что
откуда получаем, что 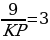 , KP=9:3=3.
, KP=9:3=3.
Ответ:3.
6







 ешение:
ешение: 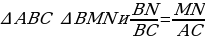 .
.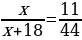 .
.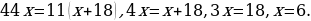

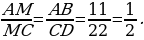
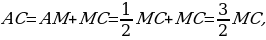 откуда
откуда 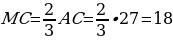 .
.
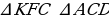 . Откуда
. Откуда 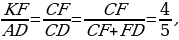 поэтому
поэтому 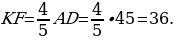
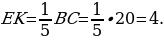 Таким образом, EF=EK+KF=4+36=40.
Таким образом, EF=EK+KF=4+36=40. 










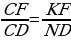 . Обозначим CF=4x, DF=x, тогда CD=x+4x=5x.
. Обозначим CF=4x, DF=x, тогда CD=x+4x=5x.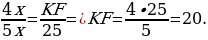



 , тогда
, тогда 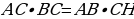 .
.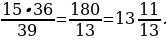
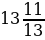 .
.
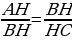 , НС=АС-АН=40-10=30.
, НС=АС-АН=40-10=30.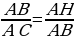 , тогда АВ2=АС·АН=40·10=400, АВ=20.
, тогда АВ2=АС·АН=40·10=400, АВ=20.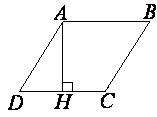
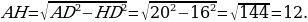

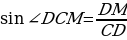 .
.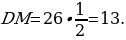
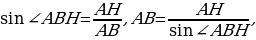
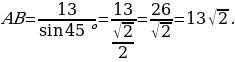
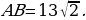
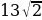 .
.
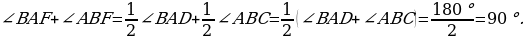
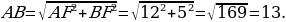

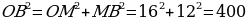 , откуда ОВ = 20.
, откуда ОВ = 20.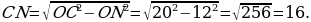
 , откуда ОВ = 25.
, откуда ОВ = 25.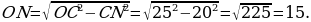

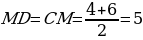 , MK=MD-KD=5-4=1.
, MK=MD-KD=5-4=1.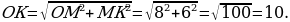

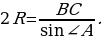
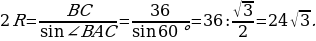
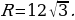
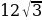 .
.
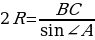 .
.


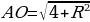 .
.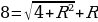 ,
,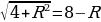 ,
,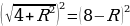 ,
,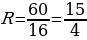 ,
,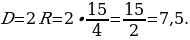

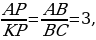 откуда получаем, что
откуда получаем, что 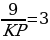 , KP=9:3=3.
, KP=9:3=3.




















