Учебный мультимедийный проект Удивительный мир симметрии

 Я в листочке, я в кристалле,

         Я в живописи, архитектуре,

         Я в геометрии, я в человеке.
         Одним я нравлюсь, другие
         Находят меня скучной.
         Но все признают, что
                                  Я – элемент красоты.

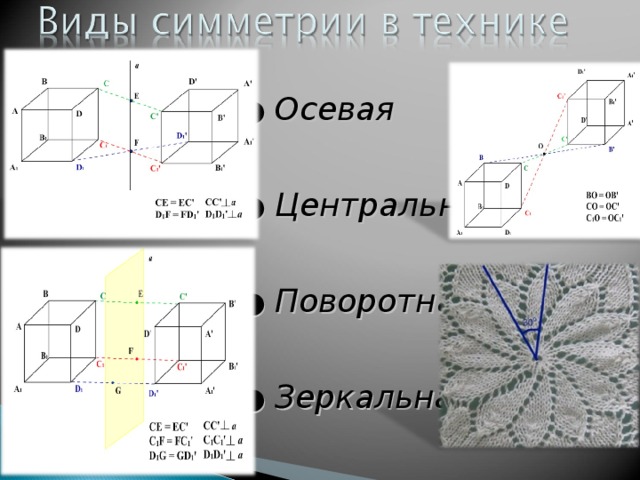
Понятие симметрии хорошо знакомо и играет важную роль в повседневной жизни. Многим творениям человеческих рук умышленно придается симметричная форма как из эстетических, так и практических соображений. Мяч симметричен, так как выглядит одинаково, как бы его ни поворачивали вокруг центра. Круглая печная труба сохраняет свой внешний вид при более ограниченном наборе вращений — поворотах вокруг вертикальной оси, проходящей через центр поперечного сечения.

Известный немецкий математик нашего столетия Герман Вейль дал     определение симметрии таким образом: «Симметрия является той идеей, с      помощью которой человек веками пытается объяснить и создать порядок,     красоту и совершенство».

В природе симметрия также встречается в изобилии. Снежинка обладает удивительнейшей гексагональной симметрией. Кристаллы также имеют характерные геометрические формы — вспомним хотя бы кубическую форму кристаллов соли, отражающую регулярность атомной структуры. Падающая дождевая капля имеет форму идеальной сферы и, замерзая, превращается в ледяной шарик — градину.

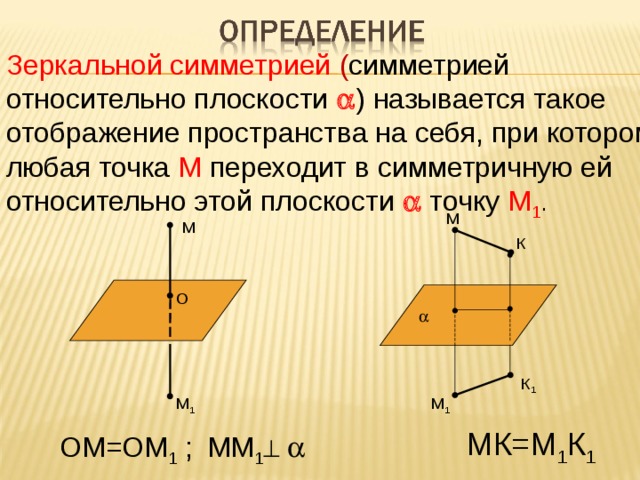
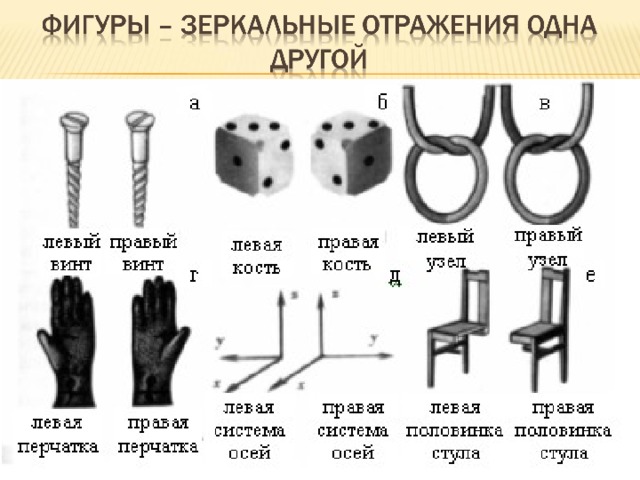
Другой вид симметрии, часто наблюдаемый в природе и в созданных человеком вещах, — так называемая зеркальная симметрия. Человеческое тело обладает (приближенно) зеркальной симметрией относительно вертикальной оси. В зеркале правая и левая руки и другие части тела меняются местами, но видимое нами зеркальное отражение узнаваемо. Многие архитектурные сооружения, например арки или соборы, обладают зеркальной симметрией.

Проект «Этот удивительный мир симметрии» реализуется в рамках изучения темы "Геометрические преобразования" в курсе основной школы. (Примеры движений фигур. Осевая, центральная и зеркальная симметрии и параллельный перенос).

Симметрия играет важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своем многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии.

Задачи проекта: знакомство учащихся с симметрией - одним из видов преобразования пространства. В ходе работы над проектом учащиеся расширяют кругозор о принципах построения окружающего мира, углубляют знания за счет самостоятельного поиска дополнительного материала, отбора и решения задач, учатся различать симметричные и несимметричные объекты, получают представления о видах симметрии. Приобретают умения преодолевать трудности, навыки работы в команде, публичного выступления, работы в программах PowerPoint, Publisher.

1. образовательные цели:

• систематизировать сведения о симметрии;

• формировать умение видеть проявление симметрии в различных областях науки (алгебре, геометрии) и деятельности человека (музыке и архитектуре);

• закрепить и систематизировать, знания, связанные с четностью и нечетностью функции;

• расширить представление учащихся о линиях на плоскости;

2. развивающие цели:

• развивать умение сравнивать, анализировать, обобщать и делать выводы;

• развивать любознательность; интеллектуальную сферу личности;

• развивать умения учебно-познавательной деятельности (развивать культуру устной и письменной речи);

Проект межпредметный, поэтому стартовая презентация может быть представлена на различных уроках.

Учащиеся формируют такие качества и умения XXI века, как: интеллектуальные, коммуникативные, оценочные, организационные.

Проект ориентирован на учащихся 10-х классов, только что начавших изучать тему «симметрия в пространстве» по математике, в ходе которого они проведут самостоятельные исследования, , “покопаются” в научной литературе и статьях Интернета, в результате чего расширят старые и приобретут новые компетентности. Преимущества данного проекта - его краткосрочность, выполняется во внеурочной деятельности

Проект включает работу по различным предметам: математика, физика, химия, биология, география, технология, архитектура, краеведение и опирается на соответствующие стандарты.

Учащимся в проекте предлагается найти примеры симметрий в окружающем мире, определить ее вид, найти центры и оси, объяснить происхождение и ответить на основополагающий вопрос ВЛАСТВУЕТ ЛИ СИММЕТРИЯ НАД МИРОМ?

Задание учащиеся выполняют по группам, формируемым по интересам (математика, биология, география, и др.).

• Тема проекта содействует генерированию новых идей и их обмену с другими, пониманию взаимосвязей в сложных системах, развитию критического мышления.

• Рассмотрение темы с различных точек зрения позволит учащимся проявить навыки устного, письменного, мультимедийного и сетевого общения, умения работать в команде, продемонстрировать толерантное поведение, открытость, терпимость разнообразным точкам зрениям.

• В созданом портфолио проекта учащиеся продемонстрируют такие информационные и медийные навыки как умение находить, анализировать, обрабатывать, интегрировать, оценивать и создавать информацию в разных формах и на различных типах медиаоборудования.

• Проект ориентирован на выполнение государственных стандартов. Например, по математике - преобразования графиков: параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой y = x, растяжение и сжатие вдоль осей координат. Многогранники. Симметрии в кубе, в параллелепипеде, в призме и пирамиде. Понятие о симметрии в пространстве (центральная, осевая, зеркальная). Примеры симметрий в окружающем мире.

После завершения проекта учащиеся группы математиков смогут находить центры и оси симметрии, выполнять преобразования графиков: параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой y = x, растяжение и сжатие вдоль осей координат. Приводить примеры симметрии в окружающем мире.

После завершения проекта учащиеся группы географов смогут подмечать проявление симметрии в живой и неживой природе, архитектурных достопримечательностях, определять виды симметрии, находить её центры и оси, объяснять происхождение.

Проблемные вопросы

По каким направлениям можно оценивать симметричность мира?

По каким направлениям (с точки зрения математики) можно оценивать симметрию?

Учебные вопросы

Где можно представить симметрию в пространстве?

Симметрия – это красота, гармония, совершенство?

Симметрична ли красота?

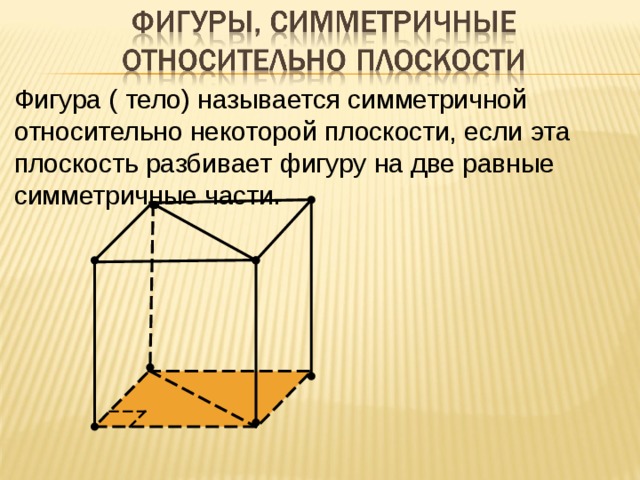
Какие оси и центры симметрии присутствуют в кубе, в параллелепипеде, в призме и пирамиде? Какие виды симметрии встречаются в пространстве? (центральная, осевая, зеркальная)?

Симметрия – фундаментальное свойство природы

Как симметрия проявляется в неживой природе? Какие архитектурные достопримечательности выполнены по законам симметрии?

План проекта

Представление проблемной ситуации: Учителю необходимо провести мозговой штурм с учащимися с целью выявления имеющихся знаний учащихся по проблеме, их мотивацию, наклонности и интересы. Инструмент - мозговой штурм с помощью стартовой презентации. С помощью презентации учитель создает проблемную ситуацию, организует мозговую атаку, обсуждение возникших вопросов, выдвижение гипотез и распределение учащихся по тематическим группам с учетом интересов. На родительском собрании с целью включения родителей в проект им предлагается познакомиться с буклетом, который дает представление о проекте и о планировании работы каждой группы. Таким образом, родители могут оказать посильную помощь в работе над проектом.

Работа над проектом: На начальном этапе работы над проектом учитель помогает каждой тематической группе распределить роли, обсудить стратегию исследования, способы поиска информации, методы исследования и возможности оформления результатов работы. Итогом является индивидуальный план деятельности. Далее начинается самостоятельная исследовательская, поисковая работа учащихся в соответствии с планом. На этом этапе учащиеся собирают информацию по теме проблемного вопроса в энциклопедиях, учебниках и в Интернете, обсуждают собранную информацию в группе, разрабатывают инструментарий исследования, проводят исследования, сравнивают его результаты с собранной информацией, делают выводы, которые будут ответом на проблемный вопрос. Основное внимание учителю следует уделить промежуточным обсуждениям, дискуссиям внутри групп, консультациям учителей-предметников и заведующего школьной теплицей по мере необходимости. Лист самооценки поможет участникам проекта осознать уровень личностного роста.

Оформление результатов проектной деятельности: Оформление результатов планируется в виде презентации, буклета или wiki-статьи, поэтому здесь может понадобиться консультация учителя информатики, на одной из консультаций необходимо обсудить с ребятами критерии оценивания данных продуктов. Одновременно с этим готовится выступление группы на открытой защите, поэтому в критерии оценивания необходимо заложить пункты оценивания выступления учащихся, умение задавать вопросы и отвечать на них.

Защита проекта, оппонирование, дискуссия: Защиту проектов можно организовать как открытое занятие, пригласить на нее родителей, учителей. В ходе защиты каждая группа представляет свою работу (презентацию, буклет или wiki-статью), отвечает на вопросы. Оценивание происходит с помощью разработанных критериев участниками группы, участниками других групп, родителями и учителями. Защита проектов позволяет ответить на основополагающий вопрос, сформулировать общие выводы по итогам работы. В ходе защиты участникам предлагается ответить на вопросы теста.

По окончании работы: Необходимым элементом всей проектной деятельности является анализ проделанной работы, где учитель обсуждает с детьми, что у них получилось, что не получилось и почему. На этом этапе можно вновь обратиться к листу самооценки и увидеть качественный рост каждого участника. Кроме того, возможна организация рефлексии в блоге. Немаловажным становится награждение групп. Представление проекта на школьной научно-практической конференции позволяет участникам проекта осознать личностную значимость, когда они делятся опытом на большой аудитории учащихся.

Учащимся предлагается подробно изучить проявление симметрии в живой и неживой природе и архитектурных достопримечательностях, рассмотреть её виды и происхождение.

Учащиеся представят результаты наблюдения и опросов в презентациях. Поддержат устное выступление использованием мультимедийных элементов: изображения и видео.

Что может быть больше похоже на мою руку или мое ухо , чем их собственное отражение в зеркале ? И все же руку которую я вижу в зеркале, нельзя поставить на место настоящей руки.

Иммануил Кант

Выполнили:

ученицы 11 А кл.

Москвина Кристина, Лосева Яна

Руководитель :

Кузина Н. В., учитель математики

Зеркальной симметрией ( симметрией относительно плоскости  ) называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей относительно этой плоскости  точку М 1 .

М

М

К



О

К 1

М 1

М 1

МК=М 1 К 1

ОМ=ОМ 1 ; ММ 1  

Если преобразование симметрии относительно плоскости переводит фигуру (тело) в себя, то фигура называется симметричной относительно плоскости, а данная плоскость – плоскостью симметрии этой фигуры. В некоторых источниках, такую симметрию называют зеркальной.

Зеркало не просто копирует объект, но и меняет местами (переставляет) передние и задние, по отношению к зеркалу, части объекта. В сравнении с самим объектом, его зазеркальный двойник оказывается вывернутым вдоль направления, перпендикулярного плоскости зеркала

Фигура ( тело) называется симметричной относительно некоторой плоскости, если эта плоскость разбивает фигуру на две равные симметричные части.

Если конус неподвижен, то его легко можно совместить со своим двойником.

Если же конус вращать относительно оси, проходящей через вершину, то направление вращения изменяется при отражении на противоположное. Теперь уже никакими перемещениями и поворотами нельзя совместить объект с зазеркальным двойником.

Симметрия относительно плоскости (зеркальная симметрия) пространства есть движение, а значит, обладает всеми свойствами движений: переводит прямую в прямую, отрезок --- в отрезок, луч --- в луч, плоскость --- в плоскость.

При симметрии относительно плоскости все точки этой плоскости, и только они, остаются на месте (неподвижные точки преобразования). Прямые, лежащие в плоскости симметрии и перпендикулярные ей, переходят в себя. Плоскости, перпендикулярные плоскости симметрии также переходят в себя.

Александринский

театр

Исаакиевский собор

Зеркальная симметрия в мировой архитектуре

Зеркальная симметрия в природе.

Технические объекты – самолёты, автомашины, ракеты, молотки, гайки – практически все они от мала до велика обладают той или иной симметрией. Случайно ли это? В технике красота, соразмерность механизмов часто бывает связана с их надёжностью, устойчивостью в работе

Симметричная форма дирижабля, самолёта, подводной лодки, автомобиля и т.д. обеспечивает хорошую обтекаемость воздухом или водой, а значит, и минимальное сопротивление движению.

На заре развития авиации наши знаменитые учёные Н. Е. Жуковский и С. А. Чаплыгин исследовали полёт птиц, чтобы сделать выводы относительно наивыгоднейшей формы крыла и условий его полёта.

Большую роль в этом сыграла, конечно, симметрия .

• На заре развития авиации наши знаменитые учёные Н. Е. Жуковский и С. А. Чаплыгин исследовали полёт птиц, чтобы сделать выводы относительно наивыгоднейшей формы крыла и условий его полёта. Большую роль в этом сыграла, конечно, симметрия .
• На заре развития авиации наши знаменитые учёные Н. Е. Жуковский и С. А. Чаплыгин исследовали полёт птиц, чтобы сделать выводы относительно наивыгоднейшей формы крыла и условий его полёта. Большую роль в этом сыграла, конечно, симметрия .

● Осевая

● Центральная

● Поворотная

● Зеркальная