муниципальное бюджетное общеобразовательное учреждение
«Тирянская ОШ» Кардымовского района Смоленской области
Проект по геометрии
на тему
«Симметрия в окружающем мире»
Работу выполнила
обучающаяся 8 класса
Чебакова Инна
Руководитель
Кезикова Л.Н.
2018/2019 учебный год
Содержание.
1.Введение……………………………………………………. ………..2 стр.
2.Симметрия сквозь века……………………………………................2 стр.
3.Виды симметрии……………………………………………………...4 стр.
4. Симметрия в зоологии………………………………………………5 стр.
4.1. Симметрия простейших организмов……………………………..5 стр.
4.2.Симметрия подводного мира……………………………………...6 стр.
5.Симметрия в ботанике………………………….…………………….7 стр.
6.Симметрия в архитектуре…………………….………………………9 стр.
7.Симметрия в быту…………………………….……………………..10 стр.
8.Заключение……….…………………………………………………..11 стр.
9.Список Интернет-источников………………………………………11 стр.
«Стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна глазу? Что такое симметрия? Это врожденное чувство, отвечал я сам себе»
Л.Н. Толстой.
1. Введение
Я считаю, что тема симметрии очень актуальна и интересна. В наше время, наверное, трудно найти человека, который не имел бы какого-либо представления о симметрии. Мир, в котором мы живем, наполнен симметрией домов и улиц, гор и полей, творениями природы и человека.
С симметрией мы встречаемся буквально на каждом шагу: в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Оно встречается уже у истоков человеческого развития. Издавна человек использовал симметрию в архитектуре. Древним храмам, башням средневековых замков, современным зданиям она придает гармоничность, законченность.
Цель: изучить простейшие типы пространственной симметрии (центральную, осевую, зеркальную)
Задачи: изучить явления симметрии в зоологии, ботанике, архитектуре, транспорте и технике, химии, быту.
2. Симметрия сквозь века
По преданию термин «симметрия» придумал скульптор Пифагор Регийский, живший в городе Регул. Отклонение от симметрии он определил термином «асимметрия». О нем говорили как о первом скульпторе, в творчестве которого была сделана попытка соблюсти ритм и соразмерность. Кроме того, Пифагор прославился реалистическим изображением человеческих жил, вен и волос.
Древние греки полагали, что Вселенная симметрична просто потому, что она прекрасна. Считая сферу наиболее симметричной и совершенной формой, они делали вывод о сферичности Земли и её движении по сфере вокруг некоего «центрального огня», где двигались также 6 известных тогда планет вместе с Луной, Солнцем, звёздами. Древнегреческий философ и математик Пифагор Самосский (VI в. до н.э.) и пифагорейцы предпочитали вместо слова «симметрия» пользоваться словом «гармония». Последователи Пифагора Самосского пытались связать симметрию с числом. Каждой вещи, учили пифагорейцы, соответствует определённое отношение чисел, которое они называли логосом. Поэтому познание вещей заключалось для них познанием логоса. Гармония является божественной и заключается в числовых отношениях.
Широко используя идею гармонии и симметрии, учёные древности любили обращаться не только к сферическим формам, но и к правильным многогранникам, для построения которых они использовали «золотое отношение». У правильных многогранников грани - правильные многоугольники одного вида, а углы между гранями равны. Древние греки установили поразительный факт: существует всего пять правильных выпуклых многогранников, названия которых связаны с числом граней, - тетраэдр, октаэдр, икосаэдр, куб, додекаэдр.
Все правильные многогранники обладают и зеркальной, и поворотной симметрией. А идея симметрии являлась отправным пунктом для учёных прошлых веков в теориях о строении материи и Вселенной. Правильные многогранники изучал и сам Пифагор Самосский (V в. до н.э.), математик, философ, религиозный авторитет, основатель одной из первых математических школ. Но впервые их подробно описал Платон, поэтому математики стали называть эти фигуры Платоновыми телами. Платон сводил гармонию к пространственной симметрии. По Платону космос сферичен, а в центре сферы расположена Земля. И пифагорейцы, и Платон полагали, что материя состоит из четырёх основных элементов - огня, земли, воздуха и воды. Согласно их теории, атомы этих элементов имели форму Платоновых тел: атомы огня - форму тетраэдра, земли - форму куба, воздуха - форму октаэдра, а атомы воды - форму икосаэдра. Додекаэдр считался местожительством богов, неким эфиром.
«Симметрия - это некая «средняя мера», - считал Аристотель. Аристотель говорил о симметрии, как о таком состоянии, которое характеризуется соотношением крайностей. Из этого высказывания следует, что Аристотель, пожалуй, был ближе всех к открытию одной из самых фундаментальных закономерностей природы - закономерности о ее двойственности. Проходя сквозь века термин «симметрия» обрастал различными толкованиями. Римский врач Гален (II в. н. э.) из Пергама под симметрией понимал покой души и уравновешенности.
Идея симметрии увлекла немецкого астронома Иоганн Кеплера. Кеплер пытался построить геометрическую модель мира. Модель Солнечной системы Кеплера была создана 400 лет назад. В сферу Сатурна он вписал куб, а в куб вписал сферу Юпитера. В сферу Юпитера он вписал тетраэдр - сферу Марса, а в сферу Марса был вписан додекаэдр, в который Кеплер вписал сферу Земли. Вычислив в соответствии со своей схемой радиусы планетных сфер, он обнаружил, что отношения этих радиусов хорошо согласуются с данными, полученными из наблюдений. Это побудило Кеплера думать, что ему удалось объяснить строение солнечной системы на основе единой геометрической схемы, использующей 6 планет и 5 Платоновых тел. Но Кеплер заблуждался: планет в Солнечной системе было не 6, а 9. отношения радиусов планетных сфер случайно совпали с отношениями в геометрической схеме. Современная наука рассматривает Вселенную с позиций единства симметрии и асимметрии.
Герман Вейль - это немецкий математик. Его деятельность приходится на первую половину XX века. Именно он сформулировал определение симметрии, установил по каким признакам усмотреть наличие или, наоборот, отсутствие симметрии в том или ином случае. Таким образом, математически строгое представление сформировалось сравнительно недавно - в начале XX века. Оно достаточно сложное.
Герман Клаус Хуго Вейль родился в городе Эльмсхорне (Германия). В 1908 году окончил Геттингенский университет, в том же году защитил диссертацию и получил степень доктора философии. С 1908 до 1913 г. читал лекции в Геттингенском университете в качестве приват-доцента. С 1913 по 1930 г. - профессор Цюрихского политехнического института. В 1930 - 1933 гг. работает в Геттингенском университете. 1933 по 1955 г.г. читает лекции в Принстонском институте перспективных исследований (США). Член Национальной Академии Наук США. Автор книги «Симметрия». Герман Вейль - один из крупнейших ученых XX века, оставил глубокий след во многих разделах математики и математической физики. Вейлю, в частности, мы обязаны тем, что отдаем себе сегодня полный отчет в значении для математики и физики общего понятия симметрии. Герман Вейль сказал: "Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство ".
3. Виды симметрии
| Вид симметрии | Определение | Пример |
| Лучевая | Расположение частей тела, позволяющее разделить его на 2 равные, зеркально отражающие друг друга половины в нескольких плоскостях. | 
|
| Билатеральная (осевая) | Расположение частей тела, позволяющее разделить его на две равные, зеркально отражающие друг друга половины лишь одной плоскостью. Эта плоскость носит название оси симметрии. | 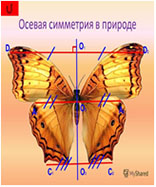
|
| Центральная | Симметрия относительно точки. Предполагает, что по обе стороны от точки, на одинаковых расстояниях находится какой либо предмет. | 
|
| Зеркальная | Зеркальная симметрия в архитектуре и природе. Отражение прибрежных зданий. Оптическое отражение в реке прибрежных деревьев.Отражение свечи в зеркале. | 
|
4. Симметрия в зоологии
Зоология - наука о животных. Она изучает многообразие животного мира, особенности строения и деятельности тела животных, их развития, распределения по земле и отношений к окружающей (живой и мертвой) природе. Конечная цель ее - выяснение законов, управляющих явлениями животного мира, объяснение с их помощью происхождение современного мира животных и установление естественной системы животных. Существует множество таких законов, и один из них это закон - симметрия. Как связаны животный мир и симметрия?
4.1. Симметрия простейших организмов
Эрнст Геккель (1834 - 1919) - немецкий естествоиспытатель, основоположник филогенетического направления дарвинизма. Основные научные работы посвящены филогенезу (историческому развитию) растений и животных, зоологии беспозвоночных. Эрнст Геккель проводил свои зоологические исследования в лаборатории и в ходе экспедиций на остров Мадейра, на Цейлон, в Египет и Алжир. Геккель публикует монографии по радиоляриям, глубоководным медузам, сифонофорам, глубоководным рыбам-удильщикам и другим обитателям подводного мира. С 1861г. Геккель – приватдоцент, а в 1865 -1909гг. - профессор Йенского университета. Умение рисовать помогло Геккелю в его работе по систематизации морских простейших. Рассматривая эти существа с помощью микроскопа, Геккель одновременно рисовал их внешний вид и строение. Первые организмы на Земле, плавающие в толще воды одноклеточные, имели максимально возможную симметрию - шаровую, они появились примерно 3,5 млрд. лет назад. Например, радиолярии. Геккель описал новые виды, обитающие в индийском океане, настоящий размер радиолярии – менее миллиметра. Пораженный открывшейся ему красотой живых форм, он создал альбом под названием «Красота форм в природе». На рисунках можно увидеть плоскости и центры симметрии. Эти рисунки хорошо иллюстрируют многовековую идею о том, что красота и строение живых организмов непосредственно связаны с симметрией.
Представитель простейших - пресноводная гидра (рис. 3). Тело достигает 1-1, 5см. Ловчие щупальца короче тела. Гидру можно обнаружить на водной растительности. Для этого необходимо выловить водоросли и оставить их на некоторое время в банке с водой, чтобы гидра расправилась. На расправившейся гидре можно увидеть тело, щупальца, окружающие ротовое отверстие, подошву. Питается гидра, захватывая своими щупальцами мелких животных. Гидру относят к многоклеточным животным, так как её тело образовано большим количеством клеток. Биологи подтверждают, что через тело гидры можно провести несколько плоскостей симметрии. Такой тип симметрии тела животного в биологии называется лучевой. Лучевая симметрия способствует тому, что животное может ловить добычу и чувствовать приближение опасности с любой стороны. Именно поэтому животные, ведущие малоподвижный образ жизни, внешне похожи на зонтики, шары и цветки растений.
4.2. Симметрия подводного мира
Для представителей подводного мира характерна центральная (поворотная) симметрия. Медуза - обладает лучевой (центральной симметрией). Морская звезда. Звездообразные или пятиугольные иглокожие. Величина колеблется от 2 см до 1 м. хотя большинство — 12—24 см. Многие виды ярко окрашены. Обнаружив двустворчатого моллюска, морская звезда обхватывает его раковину руками, присасывается к ней своими ножками и за счет мышечного напряжения раздвигает створки, для принятия пищи. Ось симметрии этих животных показывает направление силы тяжести. Морская звезда обладает поворотной симметрией пятого порядка.
Радиальная симметрия — форма симметрии, сохраняющаяся при вращении объекта вокруг определённой точки или прямой. Часто эта точка совпадает с центром тяжести объекта, то есть той точкой, в которой пересекается бесконечное количество осей симметрии. Подобными объектами могут быть круг, шар, цилиндр или конус. Тело морских ежей обычно почти сферическое, размером от 2—3 до 30 см; покрыто рядами известковых пластинок. Пластинки, как правило, соединены неподвижно и образуют плотный панцирь (скорлупу), не позволяющий ежу изменять форму. По форме тела (и некоторым иным признакам) морские ежи подразделяются на правильных и неправильных. У правильных ежей форма тела почти круглая, и построены они по строго радиальной пятилучевой симметрии. У неправильных ежей форма тела уплощённая, и у них различимы передний и задний концы тела.
Симметрия в животном мире диктуется условиями жизни. Это хорошо видно на примере рыбы камбалы. У камбалы, как и у других рыб, имеется вертикальная плоскость симметрии. Взрослая камбала лежит на дне. Ее глаза, рот, плавники переползают на одну сторону, и ее плоскость симметрии поворачивается на 90°. Камбала приобретает симметрию тела вращения, т.е. поворотную центральную симметрию.
Животные, которые способны передвигаться в каком-то избранном направлении, приобрели двустороннюю симметрию тела (осевую). На ее появление оказало влияние направление движения животного и направление силы тяжести. Однако большинство животных нашей планеты, например, майский жук, речной рак, слон, имеют одинаковые парные органы на левой и на правой сторонах тела. Такие животные появились значительно позже кишечнополостных в процессе исторического развития. Через их тело можно мысленно провести только одну плоскость, делящую их на две зеркально одинаковые половины. Такая симметрия тела называется двусторонней. Она характерна для всех активно передвигающихся животных. Двусторонняя (билатеральная) симметрия — симметричность относительно зеркального отражения. Асимметризация по оси «перед-зад» происходила при взаимодействии с пространственным полем, когда понадобилось быстрое движение (спастись от хищника, догнать жертву). В результате, в передней части тела оказались главные рецепторы и мозг. Билатерально симметричные организмы господствуют последние 650-800 млн. лет. Это ракообразные, рыбы, все прогрессивные формы: млекопитающие, птицы, насекомые. В этих направлениях животное устремляется за пищей или спасается от опасности. По наблюдениям, осевая симметрия присуща большому количеству видов животных. Еж, сова, божья коровка, бабочка, паук и другие животные обладают осевой симметрией. Например, у бабочки симметрия проявляется с математической строгостью (рис. 4). Такая симметрия способствует поступательному движению живого организма. Почему же в природе царит симметрия? Чем обусловлена эта упорядоченность, пропорциональность?
По данным науки, первые многоклеточные животные появились в воде; они произошли от колониальных простейших - жгутиковых, похожих на вольвокс, и располагались в толще воды во взвешенном состоянии, и любое перемещение для них было безразлично. Поэтому первые многоклеточные имели форму шара. По мере развития и усложнения организмов под действием силы тяжести они стали различать «верх» и «низ» и потеряли симметрию шара. Животные, ведущие прикреплённый образ жизни, такие, как гидра, приобрели симметрию, которая способствует ловле добычи и защиты от врагов, появляющихся с любой стороны. Ось симметрии этих животных показывает направление силы тяжести. Те животные, которые способны были передвигаться в каком- то избранном направлении, приобрели двустороннюю симметрию тела. На её появление важное влияние оказало как направление силы тяжести, так и направление движения животного. Для двустороннесимметричных видов характерно наличие двух примерно одинаковых частей тела, что помогает им сохранять равновесие, прямолинейно передвигаться, быстрее находить пищу и т. д.
Владимир Николаевич Беклемишев советский зоолог, действительный член АМН СССР выделил три типа симметрии (шаровая, радиальная, билатеральная) расположив их в эволюционный ряд. Считая полностью асимметричную амёбу более примитивным существом, чем одноклеточные организмы шаровой симметрии (радиолярии), он поместил её в начало ряда. Билатерально симметричные организмы считались "венцом" эволюции.
5. Симметрия в ботанике
Ботаника - наука о растениях. Ботаника - охватывает огромный круг проблем: их систематику; развитие в течение геологического времени; возможности хозяйственного использования растений; закономерности внешнего и внутреннего строения растений. Наше исследование было направлено на выявление примеров симметрии в растениях, то есть мы занимались последней из этих проблем - проблемой поиска закономерностей внешнего строения растений. В 5 веке до н. э. на явление симметрии в живой природе обратили внимание в Древней Греции пифагорейцы, в связи с развитием ими учения о гармонии. В 19 веке появлялись отдельные работы, касающиеся этой темы. А в 1961 году, как результат многовековых исследований, посвященных поиску красоты и гармонии окружающей нас природы, появилась наука биосимметрика.
У биологических объектов встречаются следующие типы симметрии:
сферическая симметрия — симметричность относительно вращений в трёхмерном
пространстве на произвольные углы.
симметрия n-порядка — симметричность относительно поворотов на угол 360° n вокруг
какой-либо оси.
двусторонняя (билатеральная) симметрия — симметричность относительно зеркального
отражения.
трансляционная симметрия — симметричность относительно сдвигов пространства в
каком-либо направлении на некоторое расстояние.
Характерная для растений симметрия конуса хорошо видна на примере фактически любого дерева. Дерево при помощи корневой системы поглощает влагу и питательные вещества из почвы, т.е. снизу, а остальные жизненно важные функции выполняется кроной, т.е. наверху. Вертикальная ориентация оси корпуса характеризует симметрию дерева. Ярко выраженной симметрией обладают листья, цветы, ветви, плоды. Нарушение некоторых из условий определяющих симметрию дерева как симметрию конуса, приводит к искривлению стволов и однобоко развитой кроны дерева. Четко выраженной симметрией обладают листья клена, дуба и т. д. Например, лист клена обладает осевой, зеркальной симметрией.
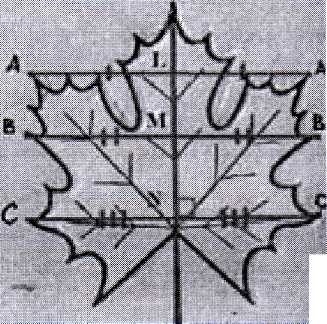
В природе встречается взаимное расположение лепестков разных видов:
зеркально равные, совместимо и зеркально равные, совместимо равные. Расположение лепестков относительно закономерно друг друга может быть: симметричным, хаотичным, асимметричным. Переносная (трансляционная) симметрия. О такой симметрии говорят тогда, когда при переносе фигуры вдоль прямой на какое-то расстояние кратное этой величине, она совмещается сама с собой. Веточка акации имеет зеркальную и переносную симметрию, а веточка боярышника обладает скользящей осью симметрии, с последующим зеркальным отражением. А цветок одуванчика обладает симметрией шара (сферической симметрией).
Центральную симметрию можно наблюдать на изображении следующих цветов: лук, цветок одуванчика, цветок кувшинки, цветок мать и мачехи. Цветок ромашки обладает центральной симметрией, только в случае четного количества лепестков. Её сердцевина представляет собой окружность, и поэтому центрально симметрична, так как мы знаем, что окружность имеет центр симметрии. В случае же нечетного количества лепестков, например анютины глазки, цветок обладает только осевой симметрией. Барвинок обладает поворотной симметрией пятого порядка и не обладает зеркальной симметрией.
О крапиве
Сорвите лист крапивы и посчитайте зубчики с левой и правой стороны. Вы убедитесь, что с одной и другой стороны одинаковое число зубцов.
О ягодах
Рассмотрим разрез любой из ягод. В поперечном разрезе она представляет собой окружность, а окружность, как нам известно, имеет центр симметрии. В продольном разрезе, например, ягода клубники обладает осевой симметрией. Поперечный разрез фруктов обладает центральной симметрией.
О грибах
Гриб в продольном разрезе обладает осевой симметрией, а шляпка гриба - центральной симметрией. Далее производится показ презентации «Геометрия цветка».
6. Симметрия в архитектуре
Прекрасные образцы симметрии демонстрируют произведения архитектуры. Большинство зданий зеркально - симметричны. Общие планы построек, фасады, орнаменты, карнизы, колонны обнаруживают соразмерность, гармонию. Много примеров использования симметрии дает старая русская архитектура: колокольни, сторожевые башни, внутренние опорные столбы.
Архитектура - удивительная область человеческой деятельности. В ней тесно переплетены и строго уравновешены наука, техника искусство. Только соразмерное, гармоничное единство этих начал делает возводимое человеком сооружение памятником архитектуры, неподвластным времени, подобно памятникам литературы.
Архитектура бесконечно разнообразна. И все же самый древний храм и современный дом, подобно человеческим лицам, имеют множество общих черт. В своем творчестве архитекторы располагают только строительным материалом и пространством. Все остальное в архитектурном облике здания архитектор создает собственной фантазией. В качестве художественных средств он использует композицию, пропорциональное соотношение здания и его частей, живопись и скульптуру, окружающую природу и застройку.
Композиция зданий. От нее в первую очередь зависит впечатление, которое производит архитектурное сооружение. Сочетание различных объемов высоких и низких, прямолинейных и криволинейных, чередование пространств открытых и закрытых. Это, пожалуй, основные приемы, которые использует зодчий, создавая архитектурные композиции.

7. Симметрия в быту


8. Заключение
Изучая симметрию, я обратила внимание на то, что законы симметрии позволяют “навести порядок” и выявить “простоту” в сложном и часто хаотическом мире эмпирических фактов. “Функция, которую несут принципы симметрии, состоит в наделении структурой законов природы или установлении между ними внутренней связи, так же как законы природы устанавливают структуру или взаимосвязь в мире явлений”. Эти слова, сказанные немецким математиком Германом Вейлем, на мой взгляд являются верными.
Работая над проектом, я убедилась, что симметрия, обнаруживаемая и в жизни, и в искусстве, и в архитектуре, и в природе является одним из принципов гармоничного построения мира. «Сфера влияния» симметрии поистине безгранична. Всюду она определяет гармонию природы, мудрость науки и красоту искусства.
В природе проявление симметрии многообразно. Насекомые, птицы и животные обладают симметрией; симметричность форм, окраски насекомых, птиц придает им красоту.
Но симметрия - это не только красота. Симметричность формы необходима рыбе, чтобы плыть, птице, чтобы летать. Так что симметрия в природе существует неспроста: она еще и полезна, или, иначе целесообразна. В природе красивое всегда целесообразно, а целесообразное – всегда красиво. Симметрия это – красота и гармония; равновесие и устойчивость.
9. Список Интернет-источников
1.http://ppt4web.ru/
2.http://ru.wikipedia.org
3. http://festival.1september.ru
4. http://lib.sfu-kras.ru/
























