Учебный проект. Свойства вневписанной окружности

Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа №15 с углубленным изучением отдельных предметов имени Героя Советского Союза Расковой Марины Михайловны » Энгельсского муниципального района Саратовской области

Свойства вневписанной окружности

Работу выполнила ученица 8Б класса

Иванова Анастасия

.Руководитель:Затеева Валентина Павловна

Цели

• Вневписанная окружность и её свойства
• Вневписанная окружность в задачах
• Сделать вывод

Определение вневписанной окружности.

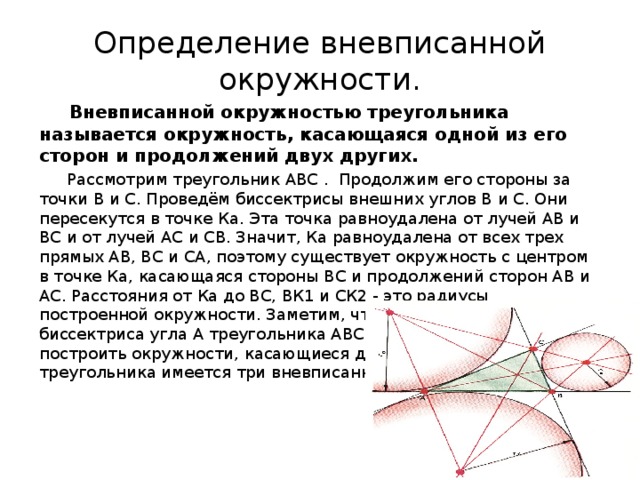
Вневписанной окружностью треугольника называется окружность, касающаяся одной из его сторон и продолжений двух других.

Рассмотрим треугольник АВС . Продолжим его стороны за точки В и С. Проведём биссектрисы внешних углов В и С. Они пересекутся в точке Ка. Эта точка равноудалена от лучей АВ и ВС и от лучей АС и СВ. Значит, Ка равноудалена от всех трех прямых АВ, ВС и СА, поэтому существует окружность с центром в точке Ка, касающаяся стороны ВС и продолжений сторон АВ и АС. Расстояния от Ка до ВС, ВК1 и СК2 - это радиусы построенной окружности. Заметим, что через Ка проходит и биссектриса угла А треугольника АВС.Аналогично можно построить окружности, касающиеся двух других сторон. Всего у треугольника имеется три вневписанных окружности .

Свойства вневписанной окружности

1)Центр вневписанной окружности в треугольник есть точка пересечения биссектрисы внутреннего угла треугольника, противолежащего той стороне треугольника, которой окружность касается, и биссектрис двух внешних углов треугольника

2) Расстояние от вершины угла треугольника до точек касания вневписанной окружности со сторонами этого угла равны полупериметру данного треугольника АВ1 = АС1 = p

3) Сумма величин, обратных радиусам вневписанных окружностей, равна величине, обратной радиусу вписанной окружности.

4) Сумма всех попарных произведений радиусов вневписанных окружностей равна квадрату полупериметра треугольника.

5) Произведение всех трех радиусов вневписанных окружностей равно произведению радиуса вписанной окружности на квадрат полупериметра треугольника.

6) Сумма радиусов вневписанных окружностей равна сумме радиуса вписанной окружности и удвоенного диаметра описанной окружности

Задача 1

Р ешение. Проведем через точку М произвольную прямую, пересекающую стороны угла в точках В и С. Построим вневписанную окружность треугольника ABC, касающуюся прямой АС в точке Т. Тогда периметр треугольника ABC равен 2AT . Для того чтобы построить треугольник с наименьшим периметром, надо прямую ВС провести так, чтобы отрезок AT, а значит и радиус вневписанной окружности, имел наименьшее значение. Это будет тогда, когда вневписанная окружность проходит через точку М. Итак, для построения треугольника с наименьшим периметром необходимо построить окружность проходящую через точку М и касающуюся сторон угла затем провести к окружности касательную в точке М. Проведенная касательная – искомая прямая

Внутри угла с вершиной А дана точка М. Через точку М проведите прямую так, чтобы она отсекала треугольник наименьшего периметра.

Задача 2

Дан квадрат ABCD со стороной а. На сторонах ВС и CD даны точки М и N такие, что периметр треугольника CMN равен 2а. Найдите угол MAN.

• Расстояния от вершины С треугольника CMN до точек В и D равны его полу периметру. Значит, В и D - точки касания вневписанной окружности, а ее центр находится в вершине А квадрата ABCD. Тогда AM и AN - биссектрисы углов BMN и MND соответственно. Далее,CMN + CNM = 90°, значит,AMN + MNA = 180° - (CMN + CNM)/2 = 135°. Откуда MAN = 180° - (AMN + MNA) = 45°.

Вывод

Вневписанная окружность широко применяется при решении геометрических задач. В данной работе передо мной стояла задача изучить свойства вневписанной окружности, я изложил задачи, приводящие к понятию вневписанной окружности, доказал ее свойства, показал ее связь с элементами треугольника и применил их к решению геометрических задач. Изученные свойства были применены при решении задач на доказательство, вычисление и построение.

Литература

https://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2014/02/09/vnevpisannaya-okruzhnost

http://www.fmclass.ru/math.php?id=4850e0d7012fd