Угол между прямой и плоскостью. Куб. Решение задач по подготовке к ЕГЭ.

Угол между прямой и плоскостью.Куб.

Автор:

Учитель математики

МБУ «гимназия №38»

Г.о.тольятти

Близнюкова Ольга Валериевна

ЗАДАЧА

В кубе A…D1 найдите угол между прямой AB и плоскостью CB1D1

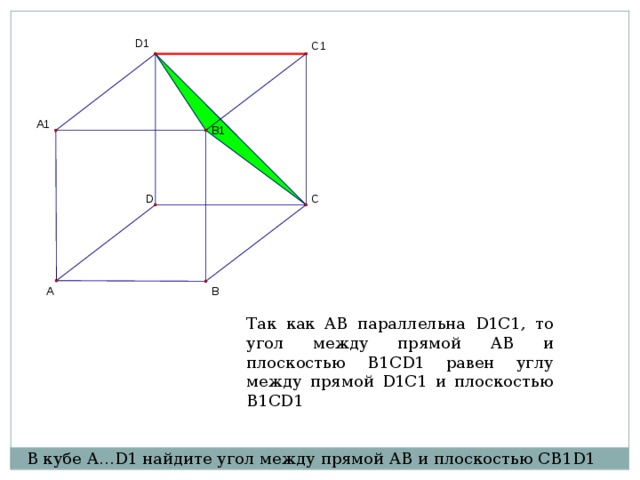
Так как AB параллельна D1C1, то угол между прямой AB и плоскостью B1CD1 равен углу между прямой D1C1 и плоскостью B1CD1

В кубе A…D1 найдите угол между прямой AB и плоскостью CB1D1

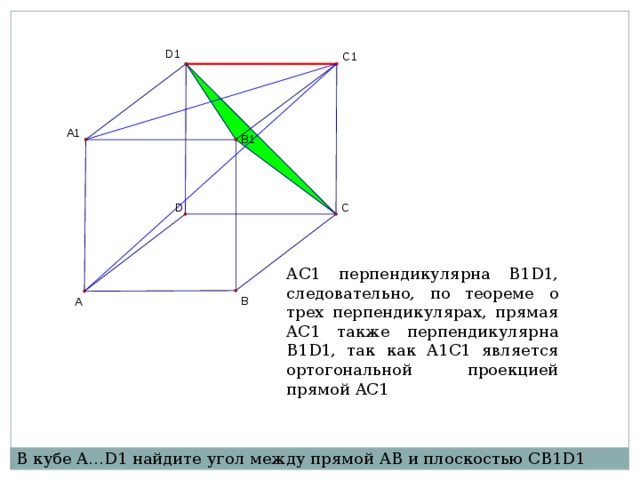
АС1 перпендикулярна B1D1, следовательно, по теореме о трех перпендикулярах, прямая AC1 также перпендикулярна B1D1, так как A1C1 является ортогональной проекцией прямой AC1

В кубе A…D1 найдите угол между прямой AB и плоскостью CB1D1

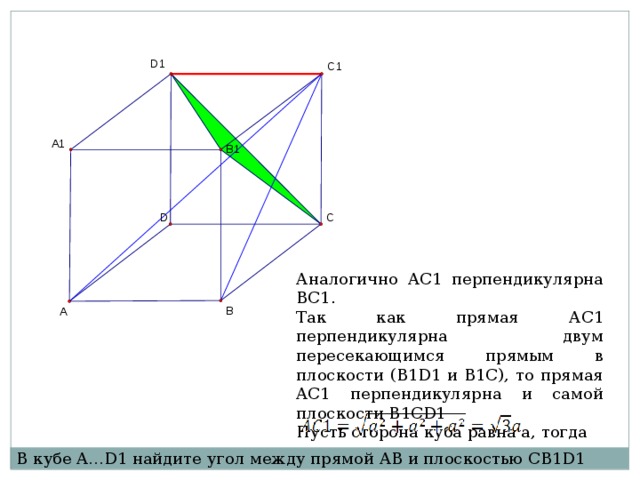
Аналогично AC1 перпендикулярна BС1.

Так как прямая АС1 перпендикулярна двум пересекающимся прямым в плоскости (B1D1 и B1C), то прямая AC1 перпендикулярна и самой плоскости B1CD1

Пусть сторона куба равна a, тогда

В кубе A…D1 найдите угол между прямой AB и плоскостью CB1D1

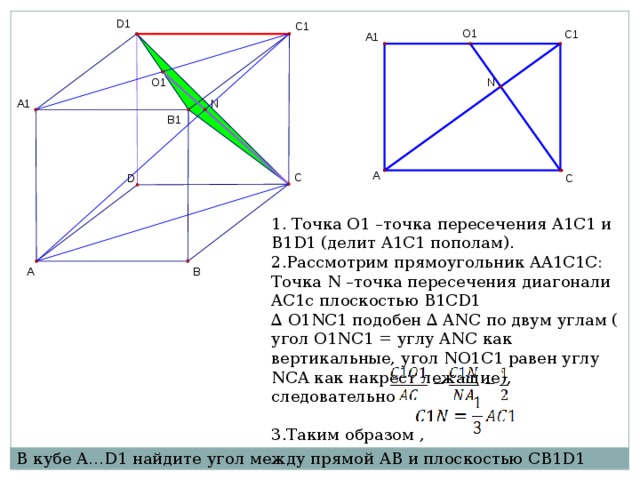
1. Точка O1 –точка пересечения A1C1 и B1D1 (делит A1C1 пополам).

2.Рассмотрим прямоугольник AA1C1C:

Точка N –точка пересечения диагонали AC1с плоскостью B1CD1

∆ O1NC1 подобен ∆ ANC по двум углам ( угол O1NC1 = углу ANC как вертикальные, угол NO1C1 равен углу NCA как накрест лежащие), следовательно

3.Таким образом ,

В кубе A…D1 найдите угол между прямой AB и плоскостью CB1D1

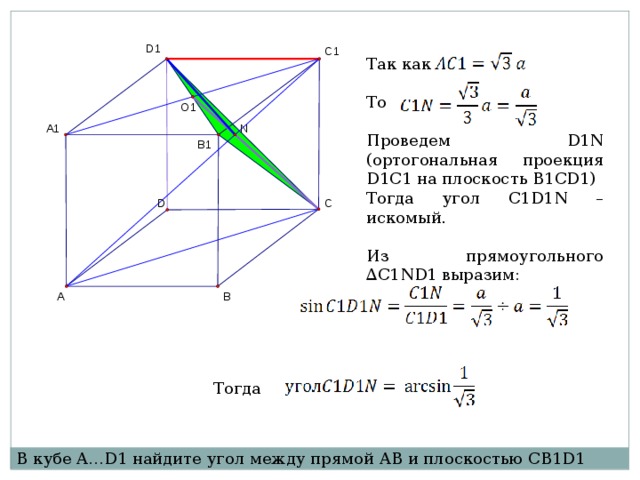
Так как

То

Проведем D1N (ортогональная проекция D1C1 на плоскость B1CD1)

Тогда угол C1D1N –искомый.

Из прямоугольного ∆C1ND1 выразим:

Тогда

В кубе A…D1 найдите угол между прямой AB и плоскостью CB1D1

Использована литература:

• Геометрия: задачи на готовых чертежах для подготовки к ЕГЭ: 10-11 классы/ Э.Н.Балаян.- Роснов н/Д: Феникс 2013.-217с.
• http://zadachi.mccme.ru