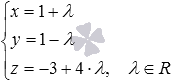Урок № ______
Предмет: ОГСЭ 05. математика
Дата проведения: 1.04.2020г Преподаватель: Касымова У.Ш.
Группа № 1-7
Тема: Угол между скрещивающимися прямыми
Цель урока: формирование понятия угла между скрещивающимися прямыми, а также умений учащихся находить углы между скрещивающимися прямыми.
Развивать мышление, память.
Воспитать интерес к уроку.
Оборудование: стереометрический набор, модели куба, тетраэдра, прямоугольного параллелепипеда.
Ход урока 1. орг. момент
2. Проверка домашнего задания
3. изучение нового материала
К определению угла между скрещивающимися прямыми будем подходить постепенно.
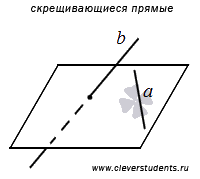
Сначала напомним определение скрещивающихся прямых: две прямые в трехмерном пространстве называются скрещивающимися, если они не лежат в одной плоскости. Из этого определения следует, что скрещивающиеся прямые не пересекаются, не параллельны, и, тем более, не совпадают, иначе они обе лежали бы в некоторой плоскости.
Приведем еще вспомогательные рассуждения.
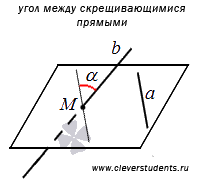
Пусть в трехмерном пространстве заданы две скрещивающиеся прямые a и b. Построим прямые a1 и b1 так, чтобы они были параллельны скрещивающимся прямым a и b соответственно и проходили через некоторую точку пространства M1. Таким образом, мы получим две пересекающиеся прямые a1 и b1. Пусть угол между пересекающимися прямыми a1 и b1 равен углу  . Теперь построим прямые a2 и b2, параллельные скрещивающимся прямым a и b соответственно, проходящие через точку М2, отличную от точки М1. Угол между пересекающимися прямыми a2 и b2 также будет равен углу
. Теперь построим прямые a2 и b2, параллельные скрещивающимся прямым a и b соответственно, проходящие через точку М2, отличную от точки М1. Угол между пересекающимися прямыми a2 и b2 также будет равен углу  . Это утверждение справедливо, так как прямые a1 и b1 совпадут с прямыми a2 и b2 соответственно, если выполнить параллельный перенос, при котором точка М1 перейдет в точку М2. Таким образом, мера угла между двумя пересекающимися в точке М прямыми, соответственно параллельными заданным скрещивающимся прямым, не зависит от выбора точки М.
. Это утверждение справедливо, так как прямые a1 и b1 совпадут с прямыми a2 и b2 соответственно, если выполнить параллельный перенос, при котором точка М1 перейдет в точку М2. Таким образом, мера угла между двумя пересекающимися в точке М прямыми, соответственно параллельными заданным скрещивающимся прямым, не зависит от выбора точки М.
Теперь мы готовы к тому, чтобы дать определение угла между скрещивающимися прямыми.
Определение.
Угол между скрещивающимися прямыми – это угол между двумя пересекающимися прямыми, которые соответственно параллельны заданным скрещивающимся прямым.
Из определения следует, что угол между скрещивающимися прямыми также не будет зависеть от выбора точки M. Поэтому в качестве точки М можно взять любую точку, принадлежащую одной из скрещивающихся прямых.
Приведем иллюстрацию определения угла между скрещивающимися прямыми.
К началу страницы
Нахождение угла между скрещивающимися прямыми.
Так как угол между скрещивающимися прямыми определяется через угол между пересекающимися прямым, то нахождение угла между скрещивающимися прямыми сводится к нахождению угла между соответствующими пересекающимися прямыми в трехмерном пространстве.
Несомненно, для нахождения угла между скрещивающимися прямыми подходят методы, изучаемые на уроках геометрии в средней школе. То есть, выполнив необходимые построения, можно связать искомый угол с каким-либо известным из условия углом, основываясь на равенстве или подобии фигур, в некоторых случаях поможет теорема косинусов, а иногда к результату приводит определение синуса, косинуса и тангенса угла прямоугольного треугольника.
Однако очень удобно решать задачу нахождения угла между скрещивающимися прямыми методом координат. Именно его и рассмотрим.
Пусть в трехмерном пространстве введена прямоугольная система координат Oxyz (правда, во многих задачах ее приходится вводить самостоятельно).
Поставим перед собой задачу: найти угол 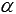 между скрещивающимися прямыми a и b, которым соответствуют в прямоугольной системе координат Oxyz некоторые уравнения прямой в пространстве.
между скрещивающимися прямыми a и b, которым соответствуют в прямоугольной системе координат Oxyz некоторые уравнения прямой в пространстве.
Решим ее.
Возьмем произвольную точку трехмерного пространства М и будем считать, что через нее проходят прямые a1 и b1, параллельные скрещивающимся прямым a и b соответственно. Тогда искомый угол 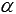 между скрещивающимися прямыми a и b равен углу между пересекающимися прямыми a1 и b1 по определению.
между скрещивающимися прямыми a и b равен углу между пересекающимися прямыми a1 и b1 по определению.
Таким образом, нам осталось найти угол между пересекающимися прямыми a1 и b1. Чтобы применить формулу для нахождения угла между двумя пересекающимися прямыми в пространстве нам нужно знать координаты направляющих векторов прямых a1 и b1.
Как же мы их можем получить? А очень просто. Определение направляющего вектора прямой позволяет утверждать, что множества направляющих векторов параллельных прямых совпадают. Следовательно, в качестве направляющих векторов прямых a1 и b1 можно принять направляющие векторы  и
и 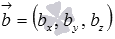 прямых a и b соответственно.
прямых a и b соответственно.
Координаты векторов 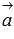 и
и 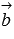 определяются либо по известным из условия уравнениям прямых a и b (смотрите раздел координаты направляющего вектора прямой), либо по известным из условия координатам двух точек прямых a и b (здесь может быть полезна теория раздела координаты вектора через координаты точек его начала и конца).
определяются либо по известным из условия уравнениям прямых a и b (смотрите раздел координаты направляющего вектора прямой), либо по известным из условия координатам двух точек прямых a и b (здесь может быть полезна теория раздела координаты вектора через координаты точек его начала и конца).
Итак, угол между двумя скрещивающимися прямыми a и b вычисляется по формуле 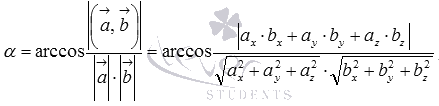 , где
, где  и
и 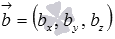 - направляющие векторы прямых a и b соответственно.
- направляющие векторы прямых a и b соответственно.
Формула для нахождения косинуса угла между скрещивающимися прямыми a и b имеет вид 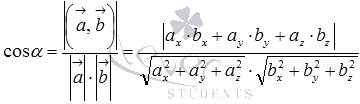 .
.
Основное тригонометрическое тождество позволяет найти синус угла между скрещивающимися прямыми, если известен косинус: 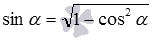 .
.
Осталось разобрать решения примеров.
Пример.
Найдите угол между скрещивающимися прямыми a и b, которые определены в прямоугольной системе координат Oxyz уравнениями 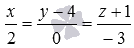 и
и 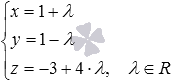
4.закрепление
Пример2. Дано изображение куба. Найдите угол между скрещивающимися прямыми а и b.
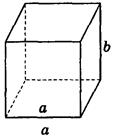
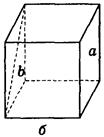
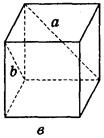
Решение задач А.В.Погорелов № 24. №25(1. 2)
|
5. Домашнее заданиие №22. №25(3,4) 6. Подведение итога урока Вопрос к классу 1) Что называется углом между скрещивающимися прямыми? 2) зависит Ли угол между скрещивающимися прямыми от выбора прямых, которые пересекаются? 3) Сформулировать обобщенное определение перпендикулярности прямой и плоскости. 4) Сформулируйте обобщенную признак перпендикулярности прямой и плоскости. 5) Сформулируйте обобщенную теорему о трех перпендикуляры.
|
|







 . Теперь построим прямые a2 и b2, параллельные скрещивающимся прямым a и b соответственно, проходящие через точку М2, отличную от точки М1. Угол между пересекающимися прямыми a2 и b2 также будет равен углу
. Теперь построим прямые a2 и b2, параллельные скрещивающимся прямым a и b соответственно, проходящие через точку М2, отличную от точки М1. Угол между пересекающимися прямыми a2 и b2 также будет равен углу 
 и
и  прямых a и b соответственно.
прямых a и b соответственно. и
и  определяются либо по известным из условия уравнениям прямых a и b (смотрите раздел ), либо по известным из условия координатам двух точек прямых a и b (здесь может быть полезна теория раздела ).
определяются либо по известным из условия уравнениям прямых a и b (смотрите раздел ), либо по известным из условия координатам двух точек прямых a и b (здесь может быть полезна теория раздела ). , где
, где  .
. .
. и
и 





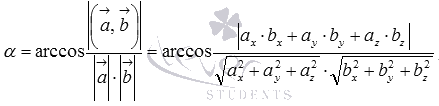 , где
, где 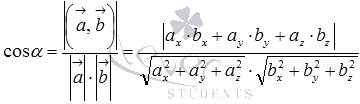 .
.