9 класс
ГЛАВА IX. ВЕКТОРЫ.
§ 3. Умножение вектора на число. Применение векторов к решению задач.
п. 86. Произведение вектора на число.
п. 87. Применение векторов к решению задач.
п. 88. Средняя линия трапеции.
Разберёмся, каким образом происходит умножение вектора на число.
Определение. Произведением ненулевого вектора 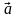 на число
на число 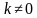 называется вектор
называется вектор 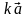 , коллинеарный данному, модуль которого равен модулю данного вектора, умноженному на модуль данного числа. Причём, если число положительное, то векторы сонаправлены, а если оно отрицательно, то векторы противоположно направлены.
, коллинеарный данному, модуль которого равен модулю данного вектора, умноженному на модуль данного числа. Причём, если число положительное, то векторы сонаправлены, а если оно отрицательно, то векторы противоположно направлены.
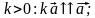
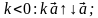
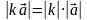
Произведение нулевого вектора на любое число равно нулевому вектору, т.е. 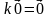 .
.
Произведение ненулевого вектора на 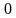 равно также нулевому вектору, т.е.
равно также нулевому вектору, т.е. 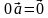 .
.
Обратим внимание ещё на такую закономерность.
Для операции умножения вектора на число справедливы алгебраические законы.
ТЕОРЕМА. Для любых векторов  и чисел
и чисел  справедливы равенства:
справедливы равенства:
 (сочетательный закон)
(сочетательный закон)
 (I распределительный закон)
(I распределительный закон)
 (II распределительный закон)
(II распределительный закон)
Доказательство.
I. Докажем сочетательный закон.
1). Если  , то числа
, то числа 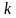 и
и  имеют одинаковые знаки (либо оба положительные, либо оба отрицательные). Значит,
имеют одинаковые знаки (либо оба положительные, либо оба отрицательные). Значит,  .
.
а) Если 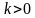 и
и  , то . Аналогично,
, то . Аналогично,  .
.
б) Если 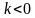 и
и  , то . Аналогично,
, то . Аналогично,  .
.
Значит,  .
.
2). Если  , то числа
, то числа 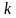 и
и  имеют разные знаки (одно число положительное, другое отрицательное). Значит,
имеют разные знаки (одно число положительное, другое отрицательное). Значит,  .
.
а) Если 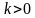 и
и  , то . Аналогично,
, то . Аналогично,  .
.
б) Если 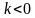 и
и  , то . Аналогично,
, то . Аналогично,  .
.
Значит, , т.е.  .
.
3). Докажем теперь равенство модулей.
Мы показали, что векторы  и
и  сонаправлены и равны по модулю, значит, эти векторы равны, т.е.
сонаправлены и равны по модулю, значит, эти векторы равны, т.е.  . Сочетательный закон доказан.
. Сочетательный закон доказан.
II. Теперь докажем первый распределительный закон.
1). Если  , то
, то  и
и  . Равенство выполняется.
. Равенство выполняется.
2). Пусть 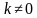 . Рассмотрим случай с неколлинеарными векторами
. Рассмотрим случай с неколлинеарными векторами 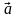 и
и  (поскольку с коллинеарными векторами доказательство тривиально).
(поскольку с коллинеарными векторами доказательство тривиально).
а) Отметим точку  и отложим от неё вектор
и отложим от неё вектор  , от точки
, от точки  отложим вектор
отложим вектор  . Вектором суммы этих векторов является вектор
. Вектором суммы этих векторов является вектор  .
.
б
) Отметим точку  и отложим от неё вектор
и отложим от неё вектор  , и от точки
, и от точки  отложим вектор
отложим вектор  . Вектором суммы этих векторов является вектор .
. Вектором суммы этих векторов является вектор .
в) Рассмотрим  и
и  .
.
(по II признаку подобия треугольников). Значит, все стороны у этих треугольников пропорциональны с одинаковым коэффициентом подобия, т.е. . Учитывая пункты а) и б), получаем:  .
.
г). По определению произведения вектора на число,
если 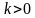 , то
, то  ;
;
если 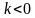 , то .
, то .
С другой стороны,
если 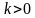 , то
, то  ;
;
если 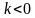 , то
, то  .
.
Мы определили, что при одном и том же знаке числа 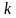 левая и правая части доказываемого равенства являются сонаправленными векторами, т.е.
левая и правая части доказываемого равенства являются сонаправленными векторами, т.е.  .
.
Из пунктов в) и г) следует, что  .
.
III. Докажем второй распределительный закон.
1). Если  , то
, то  и
и  . Равенство выполняется.
. Равенство выполняется.
2). Если  , то возможны два случая: когда
, то возможны два случая: когда 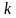 и
и  имеют одинаковые знаки, т.е.
имеют одинаковые знаки, т.е.  , и когда они имеют разные знаки, т.е.
, и когда они имеют разные знаки, т.е.  . Причём, в обоих случаях
. Причём, в обоих случаях  и
и  коллинеарны. Пусть
коллинеарны. Пусть  (в противном случае поменяем местами
(в противном случае поменяем местами 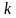 и
и  в доказываемом равенстве).
в доказываемом равенстве).
а) Пусть 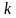 и
и  имеют одинаковые знаки, т.е.
имеют одинаковые знаки, т.е.  . Тогда Значит,
. Тогда Значит, 
б) Пусть 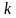 и
и  имеют разные знаки, т.е.
имеют разные знаки, т.е.  (при доказательстве не важно, какое из этих чисел отрицательно, а какое положительно). Тогда
(при доказательстве не важно, какое из этих чисел отрицательно, а какое положительно). Тогда  Значит,
Значит, 
Векторы  . Направление этих векторов совпадает с направлением вектора
. Направление этих векторов совпадает с направлением вектора 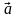 при
при 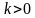 и противоположно при
и противоположно при 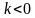 . Следовательно,
. Следовательно,  , а, значит,
, а, значит, 
Теорема полностью доказана.
Доказанные нами свойства действий с векторами позволяют упрощать выражения, содержащие векторы, по алгебраическим законам.
Например, .
Многие геометрические задачи легче решаются, если применить векторы. Мы сначала докажем свойство средней линии трапеции с помощью векторов, а затем разберём несколько задач.
Определение. Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.
– средняя линия трапеции.
ТЕОРЕМА. Средняя линия трапеции параллельна её основаниям и равна их полусумме.
Дано:  – трапеция
– трапеция

 – средняя линия
– средняя линия
Доказать:
Доказательство.
Применим векторный способ доказательства.
1). По правилу многоугольника, . С другой стороны,
Найдём сумму этих двух равенств:
 (т.к.
(т.к.  – середина
– середина  )
) 
 (т.к.
(т.к.  – середина
– середина  )
)
Значит, и .
2). Чтобы доказать параллельность средней линии основаниям, необходимо доказать, что вектор  сонаправлен с вектором суммы
сонаправлен с вектором суммы  (коэффициент
(коэффициент  , поэтому он не изменяет направление вектора суммы). Поскольку
, поэтому он не изменяет направление вектора суммы). Поскольку  то вектор суммы
то вектор суммы  сонаправлен с каждым из этим векторов. Значит, и вектор . По определению сонаправленных векторов, они лежат на параллельных прямых. Поэтому, .
сонаправлен с каждым из этим векторов. Значит, и вектор . По определению сонаправленных векторов, они лежат на параллельных прямых. Поэтому, .
Теорема доказана.
Решим несколько задач с применением векторов.
-
Доказать, что если  – середина отрезка
– середина отрезка  и
и  – произвольная точка, не лежащая на отрезке
– произвольная точка, не лежащая на отрезке  , то выполняется равенство .
, то выполняется равенство .
Дано:  – отрезок,
– отрезок, 
 – середина
– середина  ,
,
 .
.
Доказать: .
Доказательство.
Выразим вектор  из двух разных треугольников:
из двух разных треугольников:  и
и  по правилу треугольника.
по правилу треугольника.


Полученные два равенства почленно прибавим:
Векторы  и
и  являются противоположными, т.к.
являются противоположными, т.к.  (точка
(точка  – середина
– середина  ), они лежат на одной прямой и направлены в разные стороны. Значит,
), они лежат на одной прямой и направлены в разные стороны. Значит,  . Тогда,
. Тогда,
Утверждение доказано.
Из этой задачи можно сделать вывод о свойстве вектора медианы треугольника:
Вектор, выходящий из вершины треугольника в середину противолежащей стороны, равен полусумме векторов, выходящих из этой же вершины в остальные вершины треугольника.
-
В треугольнике  проведены медианы
проведены медианы  и
и  . Докажите, что .
. Докажите, что .
Дано: 
 – медианы
– медианы
Доказать: .
Доказательство.
Используя свойство вектора медианы треугольника, находим векторы  и
и  .
.
Найдём разность этих векторов:
Что и требовалось доказать.
Во многих задачах, которые решаются с применением векторов используется свойство средних линий четырёхугольника.
ТЕОРЕМА ВАРИНЬОНА.
Середины сторон произвольного плоского или «пространственного» четырёхугольника являются вершинами параллелограмма.
 – четырёхугольник
– четырёхугольник
 и
и  – средние линии четырёхугольника
– средние линии четырёхугольника
 – параллелограмм.
– параллелограмм.
-
Даны два треугольника  и
и  , имеющие общую медиану
, имеющие общую медиану  . Докажите, что
. Докажите, что  .
.
-
Даны треугольник  и точка
и точка  . Докажите, что если
. Докажите, что если  – точка пересечения медиан, то .
– точка пересечения медиан, то .
-
Дан треугольник  .
.  – точка пересечения его медиан. Докажите, что для любой точки
– точка пересечения его медиан. Докажите, что для любой точки  имеет место соотношение .
имеет место соотношение .
-
Дано, что точки  и
и  – точки пересечения медиан треугольников
– точки пересечения медиан треугольников  и
и  . Докажите, что .
. Докажите, что .
-
На сторонах  и
и  треугольника
треугольника  даны соответственно точки
даны соответственно точки  и
и  такие, что . Вычислите сумму векторов
такие, что . Вычислите сумму векторов  .
.
-
Через середину  медианы
медианы  треугольника
треугольника  проведена прямая
проведена прямая  , пересекающая сторону
, пересекающая сторону  в точке
в точке  . Докажите, что
. Докажите, что  .
.
-
Треугольники  и
и  имеют общую точку пересечения медиан. Докажите, что
имеют общую точку пересечения медиан. Докажите, что  .
.
-
На сторонах  и
и  треугольника
треугольника  даны соответственно пары точек
даны соответственно пары точек  , причём,
, причём,  . Докажите, что точки пересечения медиан треугольников
. Докажите, что точки пересечения медиан треугольников  и
и  симметричны относительно точки пересечения медиан данного треугольника.
симметричны относительно точки пересечения медиан данного треугольника.
-
Через вершины  и
и  треугольника
треугольника  параллельно направлению вектора
параллельно направлению вектора  проведены прямые, пересекающие прямые
проведены прямые, пересекающие прямые  и
и  соответственно в точках
соответственно в точках  и
и  . Докажите, что
. Докажите, что  , если .
, если .
-
На прямых  и
и  , определяющих треугольник
, определяющих треугольник  , даны соответственно точки
, даны соответственно точки  и
и  такие, что . Докажите, что если точки
такие, что . Докажите, что если точки  и
и  принадлежат одной прямой, то
принадлежат одной прямой, то  . Проверьте истинность обратного утверждения.
. Проверьте истинность обратного утверждения.
-
На плоскости даны четыре прямые, из которых никакие три не проходят через одну точку и никакие две не параллельны. Докажите, что если одна из четырёх прямых параллельна медиане треугольника, определяемого тремя другими, то аналогичными свойствами обладает каждая из трёх остальных данных прямых.
-
Через вершины  и
и  треугольника
треугольника  проведены соответственно прямые
проведены соответственно прямые  и
и  , пересекающиеся в точке
, пересекающиеся в точке  . Докажите, что прямые
. Докажите, что прямые  и
и  , проходящие соответственно через середины
, проходящие соответственно через середины  и
и  сторон
сторон  и
и  параллельно
параллельно  и
и  , также пересекаются в одной точке.
, также пересекаются в одной точке.
-
Даны треугольник  и точка
и точка  ; точки
; точки  и
и  – середины его сторон
– середины его сторон  и
и  . Через вершины
. Через вершины  и
и  проведены прямые, параллельные прямым
проведены прямые, параллельные прямым  соответственно. Докажите, что эти прямые пересекаются в одной точке.
соответственно. Докажите, что эти прямые пересекаются в одной точке.
-
На сторонах треугольника  вне его построены равносторонние треугольники
вне его построены равносторонние треугольники  . Докажите, что .
. Докажите, что .
-
На сторонах треугольника  вне его построены правильные треугольники
вне его построены правильные треугольники  . Докажите, что точки пересечения медиан треугольников
. Докажите, что точки пересечения медиан треугольников  и
и  совпадают.
совпадают.
-
На продолжениях высот  и
и  треугольника
треугольника  за его вершины
за его вершины  и
и  отложены отрезки
отложены отрезки  и
и  , причём,
, причём,  и
и  . Докажите, что
. Докажите, что  и
и  .
.
-
Даны треугольник  и центр
и центр  вписанной в него окружности. Докажите равенство , где
вписанной в него окружности. Докажите равенство , где  и
и  – длины отрезков
– длины отрезков  и
и  соответственно.
соответственно.
-
В треугольнике  проведена медиана
проведена медиана  .
.
-
Докажите, что .
-
Прямая  , параллельная прямой
, параллельная прямой  , пересекает прямые
, пересекает прямые  и
и  соответственно в точках
соответственно в точках  . Докажите, что сумма
. Докажите, что сумма  не зависит от выбора прямой
не зависит от выбора прямой  .
.
-
Прямая  пересекает отрезки
пересекает отрезки  и
и  соответственно в точках
соответственно в точках  и
и  . Докажите, что .
. Докажите, что .
-
Дан треугольник  . Докажите, что , где
. Докажите, что , где  – точка пересечения медиан треугольника,
– точка пересечения медиан треугольника,  – произвольная точка плоскости.
– произвольная точка плоскости.
-
В треугольнике  проведена биссектриса
проведена биссектриса  . Докажите, что , где
. Докажите, что , где  и
и  – длины отрезков
– длины отрезков  и
и  соответственно.
соответственно.
-
В окружность с центром  вписан треугольник
вписан треугольник  . Докажите, что , где
. Докажите, что , где  – точка пересечения высот треугольника.
– точка пересечения высот треугольника.
-
Дан треугольник  , в котором проведены медианы. Докажите, что если
, в котором проведены медианы. Докажите, что если  – середины медиан, то для любой точки
– середины медиан, то для любой точки  плоскости выполняется равенство .
плоскости выполняется равенство .
-
Докажите, что медианы произвольного треугольника  пересекаются в одной точке
пересекаются в одной точке  , которая обладает следующим свойством: расстояние от точки
, которая обладает следующим свойством: расстояние от точки  до каждой вершины треугольника равно
до каждой вершины треугольника равно  длины соответствующей медианы.
длины соответствующей медианы.
-
Существует ли в плоскости треугольника  точка
точка  , удовлетворяющая равенству ?
, удовлетворяющая равенству ?
-
Из точки  , лежащей внутри треугольника
, лежащей внутри треугольника  , проведены перпендикуляры на стороны
, проведены перпендикуляры на стороны  и на этих перпендикулярах отложены отрезки
и на этих перпендикулярах отложены отрезки  , равные соответствующим сторонам треугольника. Докажите, что
, равные соответствующим сторонам треугольника. Докажите, что  – центр масс треугольника
– центр масс треугольника  .
.
-
На сторонах треугольника  вне его построены квадраты, имеющие центры соответственно в точках
вне его построены квадраты, имеющие центры соответственно в точках  . Докажите, что .
. Докажите, что .
-
На сторонах  и
и  треугольника
треугольника  вне его построены квадраты
вне его построены квадраты  и
и  . Докажите, что медиана треугольника
. Докажите, что медиана треугольника  , проведённая через вершину
, проведённая через вершину  , перпендикулярна стороне
, перпендикулярна стороне  и равна её половине.
и равна её половине.
-
Дан параллелограмм  . Точка
. Точка  – его центр. Докажите, что если
– его центр. Докажите, что если  – любая точка плоскости, то .
– любая точка плоскости, то .
-
Дан параллелограмм  . На прямой
. На прямой  взята такая точка
взята такая точка  , что
, что  . Прямая
. Прямая  пересекает прямую
пересекает прямую  в точке
в точке  , для которой
, для которой  . Вычислите
. Вычислите  .
.
-
Через вершину  параллелограмма
параллелограмма  проведена прямая
проведена прямая  , пересекающая прямые
, пересекающая прямые  и
и  соответственно в точках
соответственно в точках  и
и  . Докажите, что если , то
. Докажите, что если , то  .
.
-
Дан параллелограмм  . Найдите на плоскости такую точку
. Найдите на плоскости такую точку  , чтобы выполнялось равенство . Сколько существует таких точек?
, чтобы выполнялось равенство . Сколько существует таких точек?
-
Дан параллелограмм  . Докажите, что , где
. Докажите, что , где  – произвольная точка пространства.
– произвольная точка пространства.
-
 - параллелограмм,
- параллелограмм,  – его центр,
– его центр,  – произвольная точка плоскости. Выразите вектор
– произвольная точка плоскости. Выразите вектор  через векторы .
через векторы .
-
Два параллелограмма  и
и  имеют общую вершину
имеют общую вершину  . Докажите, что
. Докажите, что  .
.
-
Даны два параллелограмма  и
и  . Докажите, что каждый из трёх отрезков
. Докажите, что каждый из трёх отрезков  не больше суммы двух других отрезков.
не больше суммы двух других отрезков.
-
 и
и  – два параллелограмма с центрами
– два параллелограмма с центрами  и
и  . Выразите векторы через векторы
. Выразите векторы через векторы  и
и  .
.
-
Докажите, что если в четырёхугольнике  точки
точки  и
и  – соответственно середины сторон
– соответственно середины сторон  и
и  и для построенного параллелограмма
и для построенного параллелограмма  точка
точка  - середина отрезка
- середина отрезка  , то
, то  и
и  .
.
-
На стороне  четырёхугольника
четырёхугольника  построен параллелограмм
построен параллелограмм  и взята точка
и взята точка  – середина отрезка
– середина отрезка  . Докажите, что если
. Докажите, что если  и
и  – соответственно середины сторон
– соответственно середины сторон  и
и  , то отрезок
, то отрезок  равен отрезку
равен отрезку  по длине и параллелен ему.
по длине и параллелен ему.
-
Даны два параллелограмма  и
и  . Докажите, что в общем случае середины отрезков
. Докажите, что в общем случае середины отрезков  являются вершинами параллелограмма
являются вершинами параллелограмма  . Постройте два таких параллелограмма, чтобы точки
. Постройте два таких параллелограмма, чтобы точки  совпадали или принадлежали одной прямой.
совпадали или принадлежали одной прямой.
-
Докажите, что если  – соответственно середины последовательных сторон шестиугольника, то .
– соответственно середины последовательных сторон шестиугольника, то .
-
 и
и  – два параллелограмма и
– два параллелограмма и  – центр первого из них. Выразите векторы через векторы .
– центр первого из них. Выразите векторы через векторы .
-
Даны четыре компланарных вектора одинаковой длины. Докажите, что если , то четырёхугольник  – прямоугольник.
– прямоугольник.
-
При каждой вершины треугольника  построены ромбы, стороны которых равны и направлены по сторонам треугольника;
построены ромбы, стороны которых равны и направлены по сторонам треугольника;  – диагонали этих ромбов. Докажите, что .
– диагонали этих ромбов. Докажите, что .
-
Докажите, что четырёхугольник  является параллелограммом тогда и только тогда, когда для любой точки
является параллелограммом тогда и только тогда, когда для любой точки  выполняется равенство .
выполняется равенство .
-
Докажите, что если точки  не принадлежат одной прямой и
не принадлежат одной прямой и  , то четырёхугольник
, то четырёхугольник  – параллелограмм.
– параллелограмм.
-
В четырёхугольнике  точки
точки  – соответственно середины последовательных сторон. Докажите, что
– соответственно середины последовательных сторон. Докажите, что  – параллелограмм.
– параллелограмм.
-
Дана трапеция  . Прямая, параллельная её основаниям
. Прямая, параллельная её основаниям  и
и  , пересекает боковые стороны
, пересекает боковые стороны  и
и  соответственно в точках
соответственно в точках  и
и  . Докажите, что если
. Докажите, что если  , то
, то  .
.
-
Дана трапеция  , у которой
, у которой  и
и  – основания, а точки
– основания, а точки  и
и  – середины её боковых сторон
– середины её боковых сторон  и
и  . Докажите, что
. Докажите, что  .
.
-
Через точку пересечения  диагоналей
диагоналей  и
и  трапеции
трапеции  проведена прямая, параллельная основаниям и пересекающая боковые стороны
проведена прямая, параллельная основаниям и пересекающая боковые стороны  и
и  в точках
в точках  и
и  . Докажите, что , где
. Докажите, что , где  и
и  – длины отрезков
– длины отрезков  и
и  .
.
-
Докажите, что если длина средней линии  четырёхугольника
четырёхугольника  равна полусумме длин его сторон
равна полусумме длин его сторон  и
и  (точка
(точка  принадлежит стороне
принадлежит стороне  , точка
, точка  принадлежит стороне
принадлежит стороне  ), то
), то  – трапеция или параллелограмм.
– трапеция или параллелограмм.
-
Даны четырёхугольник  и точки
и точки  и
и  (точка
(точка  принадлежит стороне
принадлежит стороне  , точка
, точка  принадлежит стороне
принадлежит стороне  ). Докажите, что вектор
). Докажите, что вектор  , где
, где  и
и  – точки пересечения средних линий четырёхугольников
– точки пересечения средних линий четырёхугольников  и
и  , не зависит от выбора точек
, не зависит от выбора точек  и
и  .
.
-
Даны четырёхугольник  и точка
и точка  . Построены точки
. Построены точки  , симметричные точке
, симметричные точке  относительно середин сторон четырёхугольника. Докажите, что
относительно середин сторон четырёхугольника. Докажите, что  .
.
-
Дан четырёхугольник  . Построен второй четырёхугольник с вершинами в точках пересечения медиан треугольников
. Построен второй четырёхугольник с вершинами в точках пересечения медиан треугольников  . Докажите, что средние линии обоих четырёхугольников пересекаются в одной точке.
. Докажите, что средние линии обоих четырёхугольников пересекаются в одной точке.
-
На сторонах  и
и  четырёхугольника
четырёхугольника  даны соответственно точки
даны соответственно точки  и
и  , такие, что . Докажите, что середины отрезков
, такие, что . Докажите, что середины отрезков  и
и  принадлежат одной прямой.
принадлежат одной прямой.
-
В пятиугольнике  точки
точки  – соответственно середины четырёх последовательных сторон, начиная от
– соответственно середины четырёх последовательных сторон, начиная от  . Найдите зависимость между векторами
. Найдите зависимость между векторами  и
и  .
.
-
В окружность с центром  вписан четырёхугольник
вписан четырёхугольник  , диагонали которого перпендикулярны и пересекаются в точке
, диагонали которого перпендикулярны и пересекаются в точке  . Выразите вектор
. Выразите вектор  через векторы
через векторы  и
и  .
.
-
Дан правильный  -угольник
-угольник  с центром
с центром  . Докажите, что
. Докажите, что
-
Даны правильный  -угольник
-угольник  с центром
с центром  и точка
и точка  . Докажите, что
. Докажите, что 
-
Даны два произвольно расположенных правильных  -угольника
-угольника  и
и  с центрами в точках
с центрами в точках  и
и  . Докажите, что
. Докажите, что 
-
Дан правильный пятиугольник  с центром
с центром  . Выразите векторы
. Выразите векторы  и
и  через векторы
через векторы  и
и  .
.
-
На сторонах четырёхугольника  вне его построены квадраты и
вне его построены квадраты и  с центрами
с центрами  соответственно. Докажите, что отрезки
соответственно. Докажите, что отрезки  и
и  равны и перпендикулярны.
равны и перпендикулярны.
-
Дан четырёхугольник  . Найдите на плоскости такую точку
. Найдите на плоскости такую точку  , чтобы выполнялось равенство . Сколько существует таких точек?
, чтобы выполнялось равенство . Сколько существует таких точек?
-
Пусть  – точка пересечения средних линий четырёхугольника
– точка пересечения средних линий четырёхугольника  и
и  – произвольная точка плоскости. Докажите, что имеет место равенство .
– произвольная точка плоскости. Докажите, что имеет место равенство .
-
Дан четырёхугольник  . Его средние линии пересекаются в точке
. Его средние линии пересекаются в точке  . Построена ломаная
. Построена ломаная  , где . Докажите, что
, где . Докажите, что  – середина отрезка
– середина отрезка  .
.
-
Пусть  – произвольный многоугольник, а
– произвольный многоугольник, а  – середины его сторон. Докажите, что для произвольной точки
– середины его сторон. Докажите, что для произвольной точки  справедливо соотношение
справедливо соотношение
.
-
Точки  и
и  являются соответственно серединами диагоналей
являются соответственно серединами диагоналей  и
и  четырёхугольника
четырёхугольника  . Докажите, что и .
. Докажите, что и .
-
Проведены четыре радиуса  и
и  окружности с центром
окружности с центром  . Докажите, что если , то
. Докажите, что если , то  – прямоугольник.
– прямоугольник.
-
На окружности с центром  даны точки
даны точки  и
и  . Касательные к окружности в этих точках пересекаются в точке
. Касательные к окружности в этих точках пересекаются в точке  . Выразите вектор
. Выразите вектор  через векторы
через векторы  и
и  , если:
, если:
-
-
-
.
-
Дана окружность с центром  и
и  – точки этой окружности. Биссектриса угла
– точки этой окружности. Биссектриса угла  пересекает окружности в точке
пересекает окружности в точке  . Выразите вектор
. Выразите вектор  через векторы
через векторы  и
и  , если:
, если:
-
-
-
.
-
Дана окружность с центром  . Проведены две равные хорды
. Проведены две равные хорды  и
и  , пересекающиеся в точке
, пересекающиеся в точке  . Докажите, что сумма векторов коллинеарна вектору
. Докажите, что сумма векторов коллинеарна вектору  .
.
-
Дана окружность с центром  . Проведены две перпендикулярные хорды
. Проведены две перпендикулярные хорды  и
и  . Хорды или их продолжения пересекаются в точке
. Хорды или их продолжения пересекаются в точке  .
.
-
Докажите, что .
-
Докажите, что середины хорд  и
и  , точка
, точка  и центр
и центр  данной окружности являются вершинами параллелограмма.
данной окружности являются вершинами параллелограмма.
6







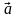 на число
на число 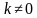 называется вектор
называется вектор 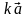 , коллинеарный данному, модуль которого равен модулю данного вектора, умноженному на модуль данного числа. Причём, если число положительное, то векторы сонаправлены, а если оно отрицательно, то векторы противоположно направлены.
, коллинеарный данному, модуль которого равен модулю данного вектора, умноженному на модуль данного числа. Причём, если число положительное, то векторы сонаправлены, а если оно отрицательно, то векторы противоположно направлены.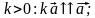
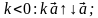
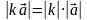
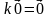 .
. 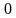 равно также нулевому вектору, т.е.
равно также нулевому вектору, т.е. 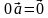 .
.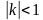 , то вектор
, то вектор 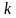 раз;
раз; , то вектор
, то вектор  , то направление вектора
, то направление вектора  , то вектор
, то вектор 
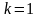 , то вектор
, то вектор 


















