Уравнение первой степени с одним неизвестным

Математический диктант

1. Любое ли положительное число можно записать в стандартном виде?

2. Укажите порядок числа

I в.

II в.

3 .Запишите число в стандартном виде:

I в.

II в.

4.Запишите число в стандартном виде:

I в.

II в.

5.Запишите число в стандартном виде:

I в.

II в.

УРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ С ОДНИМ НЕИЗВЕСТНЫМ

УРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ С ОДНИМ НЕИЗВЕСТНЫМ

• Х+5= 0
• 6-Х= 0
• 5 Х-7= 0
• 5Х +3 = 0

Х – ЭТО НЕИЗВЕСТНАЯ ПЕРЕМЕННАЯ

Общий вид уравнения первой степени с одним неизвестным

kx+b=0, k ≠0

k- коэффициент при неизвестном в уравнении.

b – свободный член уравнения

5 x -3=0

5 – коэффициент

(-3) - свободный член уравнения

КОРЕНЬ УРАВНЕНИЯ-

- ЭТО ЧИСЛО, ПРИ ПОДСТАНОВКЕ КОТОРОГО В УРАВНЕНИЕ ВМЕСТО ПЕРЕМЕННОЙ ПОЛУЧАЕТСЯ ВЕРНОЕ РАВЕНСТВО

КОРЕНЬ УРАВНЕНИЯ

ЯВЛЯЮТСЯ ЛИ ДАННЫЕ ЧИСЛА КОРНЯМИ СООТВЕТСТВУЮЩЕГО УРАВНЕНИЯ ?

• Х+5=23 Х=1; 4; 18; -9.
• 6-Х=2 Х=0; -2; 1;4.
• Х-7=12 Х=2; -5; 0; 19.
• 5Х=30 Х=6; -4; 3; 0.
• Х:7=9 Х=0; 2; -7; 63.
• 12:Х=3 Х=2; -1; 6; 4.

РЕШИТЬ УРАВНЕНИЕ-

- ЗНАЧИТ НАЙТИ ВСЕ ЕГО КОРНИ ИЛИ ДОКАЗАТЬ, ЧТО КОРНЕЙ НЕТ .

УРАВНЕНИЕ

СОСТОИТ ИЗ ДВУХ ЧАСТЕЙ : ЛЕВОЙ И ПРАВОЙ

5Х + 23 = 0

ЛЕВАЯ ЧАСТЬ ПРАВАЯ ЧАСТЬ

УРАВНЕНИЕ

ЭЛЕМЕНТЫ УРАВНЕНИЯ МОЖНО ПЕРЕНОСИТЬ ИЗ ЛЕВОЙ ЧАСТИ В ПРАВУЮ ЧАСТЬ .

ПРИ ПЕРЕНОСЕ У ЭЛЕМЕНТОВ МЕНЯЮТ ЗНАКИ НА ПРОТИВОПОЛОЖНЫЕ :

«+» НА «-»

«-» НА «+»

УРАВНЕНИЕ

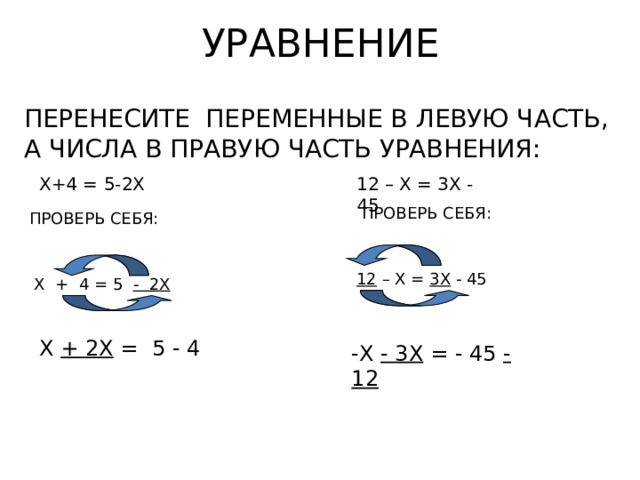
ПЕРЕНЕСИТЕ ПЕРЕМЕННЫЕ В ЛЕВУЮ ЧАСТЬ, А ЧИСЛА В ПРАВУЮ ЧАСТЬ УРАВНЕНИЯ:

Х+4 = 5-2Х

12 – Х = 3Х - 45

ПРОВЕРЬ СЕБЯ:

ПРОВЕРЬ СЕБЯ:

12 – Х = 3Х - 45

Х + 4 = 5 - 2Х

Х + 2Х = 5 - 4

-Х - 3Х = - 45 - 12

• Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю.
• Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом знак.

Чтобы решить уравнение kx +b =0, k ≠0 , надо :

• Перенести свободный член b этого уравнения в правую часть, изменив при этом знак у числа b на противоположный;
• Разделить обе части полученного уравнения на коэффициент k ( k ≠0 ) при неизвестном;

Тогда число, полученное в правой части последнего уравнения, и есть единственный корень уравнения kx +b =0,

k ≠0 .

Решить уравнения:

Домашнее задание:

С.171-173( вдумчиво прочитать, выучить определение линейного уравнения с одним неизвестным, корень уравнения)

№ 637(2 столбик)

№ 638

№ 639(3 столбик)