Тема: «График линейного уравнения с двумя переменными» Урок № 83. 19.03.19
Цели: Познакомить учащихся с понятиями линейного уравнения с двумя переменными и его решения, научить выражать из уравнения х через у или у через х.
Формируемые УУД:
Познавательные: выдвигать и обосновывать гипотезы, предлагать способы их проверки
Регулятивные: сличать способ и результат своих действий с заданным эталоном, обнаруживать отклонения и отличия от эталона; составлять план и последовательность действий.
Коммуникативные: устанавливать рабочие отношения; эффективно сотрудничать и способствовать продуктивной кооперации.
Личностные: формирование навыков организации анализа своей деятельности
Оборудование: компьютер, мультимедийный проектор, экран
Ход урока:
Этап мотивации (самоопределения) к учебной деятельности
Анализ контрольной работы № 6 – задание № 5, 2
Этап актуализации и фиксирования индивидуального затруднения в пробном действии
1) Найти числовое значение выражения 5х + 2у при:
а) х = 0; у = -1; б) х = 4; у = 0,5; в) х = -3; у = -2.
2) Найти несколько пар значений х и у, для которых значение выражения 5х + 2у равно 20. 3) Найдите точку пересечения прямых  и
и  .
.
4) Найдите координаты точки пересечения прямой, проходящей через точки А (–2;7) и В(–5;-2), и луча CD, если заданы координаты С (–6;6) и D(3;0) [Ответ: ( – 3; 4)]
Этап выявления места и причины затруднения.
Решите уравнение: 3х – 9 = 0. Давайте вспомним всё, что мы знаем о линейных уравнениях и попробуем провести параллель между известным нам материалом и новым материалом.
Какой тип уравнения нам известен? (линейное уравнение с одной переменной)
Вспомним определение линейного уравнения с одной переменной.
Что называется корнем линейного уравнения с одной переменной?
Сформулируем все свойства линейного уравнения с одной переменной.
Составьте задачу по условию: Петя купил несколько карандашей, а тетрадей на 5 больше. (Тетрадей х, карандашей у, тогда х – у = 5)
Как называется данное выражение?
Сколько переменных в данном уравнении?
Сформулируйте тему урока. А цели?
Этап построения проекта выхода из затруднения
Заполняется 1 часть таблицы
| Тип уравнения | Определение уравнения | Что является решением уравнения | Свойства |
| Линейное уравнение с одной переменной. | ах=в, где х – переменная, а,в- числа.
Пример: 3х = 6 | Значение х, при котором уравнение обращается в верное числовое равенство | 1) перенос слагаемых из одной части уравнения в другую, изменив их знак на противоположный. 2) обе части уравнения умножить или разделить на одно и тоже, не равное нулю число. |
| Линейное уравнение с двумя переменными. | ах + ву = с, где х,у – переменные, а,в.с – числа. Пример: х – у = 5 х + у = 56 2х + 6у =68 | Значения х, у, обращающие уравнение в верное числовое равенство. х=8; у=3 (8;3) х=60; у = - 4 (60;-4) | Верны свойства 1,2. 3) равносильные уравнения: х-у=5 и у=х-5 (8;3) (8;3) |
| Уравнение с двумя переменными. | ахn+ вуm = с, где х,у – переменные, а,в.с – числа. Пример 5 в учебнике стр. 179 |
|
|
После того, как заполнили первую часть таблицы, опираясь на аналогию, начинаем заполнять вторую строку таблицы, тем самым узнавать новый материал.
Этап реализации построенного проекта
Обратимся к теме: линейное уравнение с двумя переменными. Само название темы наталкивает на мысль, что нужно вводить новую переменную, например у.
Сформулируем по аналогии с определением линейного уравнения с одной переменной определение линейного уравнения с двумя переменными (Линейным уравнением с двумя переменными называется уравнение вида ax + by = c, где a,b и c – некоторые числа, а x и y –переменные).
Уравнение x – y = 5 при x = 8, y = 3 обращается в верное равенство 8 – 3 = 5. Говорят, что пара значений переменных x = 8, y = 3 является решением этого уравнения.
- Сформулируйте определение решения уравнения с двумя переменными (Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство)
Пары значений переменных иногда записывают короче: (8;3). В такой записи на первом месте пишут значение x а на втором - y.
Уравнения с двумя переменными, имеющие одни и те же решения (или не имеющие решений), называются равносильными.
Уравнения с двумя переменными обладают такими же свойствами, как и уравнения с одной переменной:
Если в уравнении перенести любой член из одной части в другую, изменив его знак, то получится уравнение равносильное данному.
Если к обеим частям уравнения прибавить одно и тоже число, то получится уравнение равносильное данному.
Если обе части уравнения умножить или разделить на одно и то же число(не равное нулю), то получится уравнение равносильное данному.
Пример 1. Рассмотрим уравнение 10x + 5y = 15. Используя свойства уравнений, выразим одну переменную через другую.
Для этого сначала перенесем 10x из левой части в правую, изменив его знак. Получаем равносильное уравнение 5y = 15 - 10x.
Разделим каждую часть этого уравнения на число 5, получим равносильное уравнение
у = 3 - 2x. Таким образом, мы выразили одну переменную через другую. Пользуясь этим равенством, для каждого значения x можно вычислить значение y.
Если x = 2, то y = 3 - 2· 2 = -1.
Если x = -2, то y = 3 - 2· (-2) = 7. Пары чисел (2; -1), (-2; 7) – решения данного уравнения. Таким образом, данное уравнение имеет бесконечно много решений.
Пример 2. Мука расфасована в пакеты по 3 кг и по 2 кг. Сколько пакетов каждого вида надо взять, чтобы получилось 20 кг муки?
Допустим, что надо взять x пакетов по 3 кг и y пакетов по 2 кг. Тогда 3x + 2y = 20. Требуется найти все пары натуральных значений переменных x и y, удовлетворяющих этому уравнению. Получаем: 2y = 20 - 3x у = 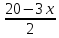
Подставляя в это равенство вместо x последовательно все числа 1,2,3 и т.д., найдем при каких значениях х, значения y являются натуральными числами.
Получаем: (2;7), (4;4), (6;1). Других пар, удовлетворяющих данному уравнению нет. Значит надо взять либо 2 и 7, либо 4 и 4, либо 6 и 1 пакетов соответственно.
Этап первичного закрепления с проговариванием во внешней речи
№ 909, № 910; № 912;
Этап включения в систему знаний и повторения: № 913; № 915; № 917
Этап рефлексии учебной деятельности на уроке (вопросы на листе информации )
Домашнее задание: п. 24, № 911, № 914, № 916