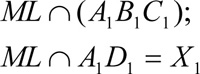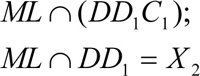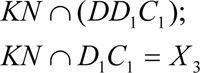Урок геометрии в 10 классе по теме: « Построение сечений многогранников» в активной среде GeoGebra.

Урок геометрии в 10 классе на тему:

« Построение сечений многогранников»

Цель урока:

Образовательная - формирование у обучающихся навыков решения

задач на построение сечений; обобщить, систематизировать и

закрепить полученные знания на предыдущих уроках; ознакомиться с

методами построений сечений многогранников;

Развивающая – развитие у учащихся пространственного и образного

мышления и воображения развитие мыслительных операций -

обобщение, классификация и анализ;

Воспитательная – Формирование у обучающихся графической

культуры, воспитывать активность и самостоятельность, аккуратность

учащихся, ответственность, уметь применять знания на практике,

интерес к предмету;

Задачи урока:

Формирования мотивации к изучению данной темы.

Умение пользоваться опорными знаниями при решении задач.

Формирование и развитие у обучающихся пространственного воображения.

Развивать у учащихся навыки творческого подхода к решению задач и

навыки исследовательской работы над задачей.

Техническое оснащение:

• компьютеры;

• проектор;

• динамическая среда GeoGebra.

Тип урока: Урок открытия новых знаний.

Форма урока: Урок - практикум с элементами развивающего обучения.

Методы обучения: объяснительно-иллюстративный, проблемно-поисковый.

Ход урока

1. Организационный момент

Здравствуйте, ребята! Какая сегодня прекрасная солнечная погода на улице! Но, боюсь, нам сейчас придется закрыть шторки, потому что сегодня у нас практическое занятие за компьютерами. Вы изучили аксиомы стереометрии, следствия из аксиом, теоремы о параллельности прямых и плоскостей в пространстве. При решении многих стереометрических задач используют сечение многогранника плоскостью. Существует несколько методов построения сечений многогранника плоскостью: метод следов, метод внутреннего проектирования и комбинированный метод. Мы изучим метод следов.

1. Объяснение нового материала

Метод следов включает три важных пункта:

1. Строится линия пересечения (след) секущей плоскости с плоскостью основания многогранника.

2. Находим точки пересечения секущей плоскости с ребрами многогранника.

3. Строим и заштриховываем сечение.

Рассмотрим пример (мультимедийный проектор).

Построить сечение куба, проходящее через точки М, N, L

Алгоритм построения

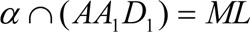
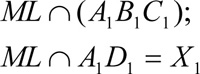
3)

4)

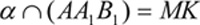
5)

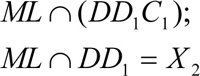
6)

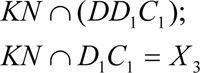
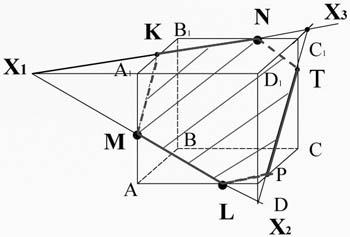
7)

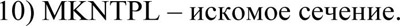
Ш. Коллективная работа за компьютерами

Сегодня же мы с вами попробуем построить сечение в динамической среде GeoGebra. Садимся по двое за компьютеры, запускаем GeoGebra и попробуем воссоздать этот апплет.

Построить сечение

1. Запускаем GeoGebra.

1. В ПАНЕЛИ ИНСТРУМЕНТОВ нажимаем ПИРАМИДА и создаем её.

На рёбрах располагаем точки согласно условию задачи. Программа автоматически именует и точки и стороны

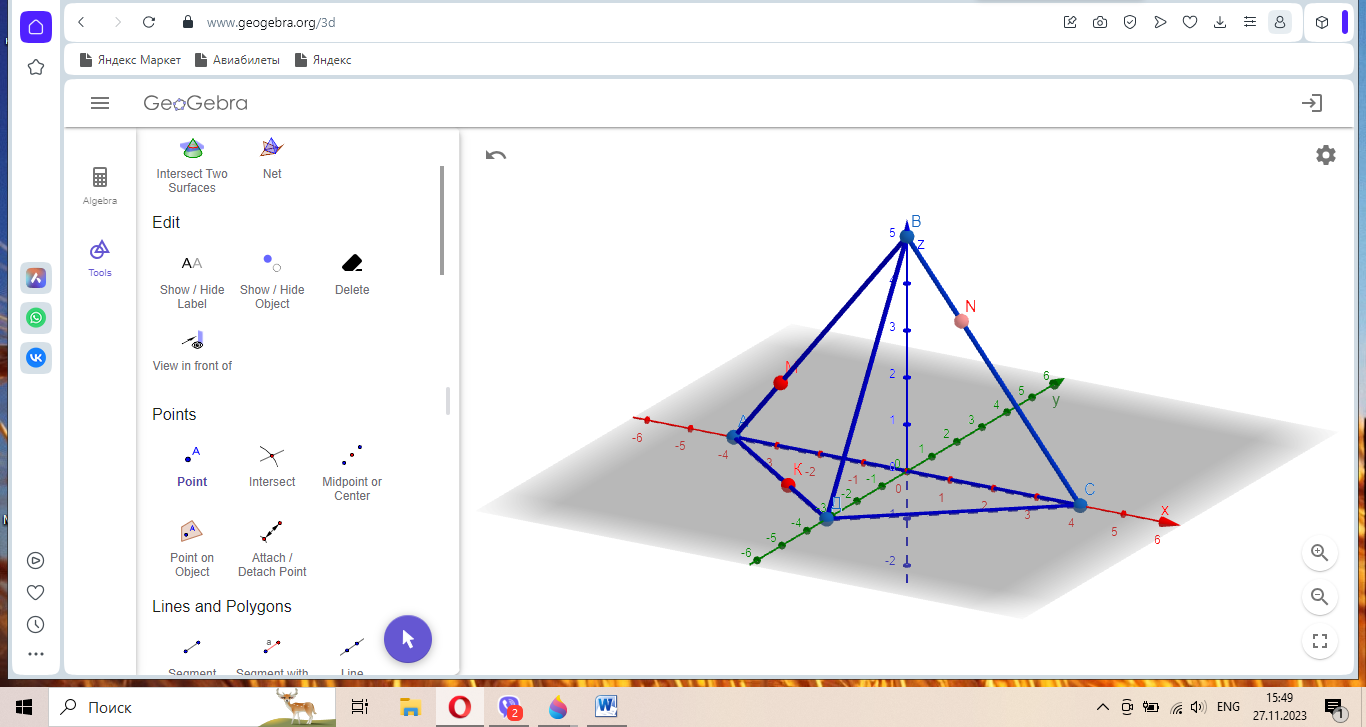
1. В ПАНЕЛИ ИНСТРУМЕНТОВ нажимаем прямая и gоследовательно нажимая по точкам М и N, Аи С, К и Х, Д и N строим прямые .

4. Очевидно, что МКFN- искомое сечение.

5. Воспользуемся кнопками ПЕРЕМЕЩАТЬ и ВРАЩЕНИЕ ОТНОСИТЕЛЬНО плоскости, а также АНИМАЦИЯ можно сделать вывод: сечением проходящим через данные точки является четырёхугольник.

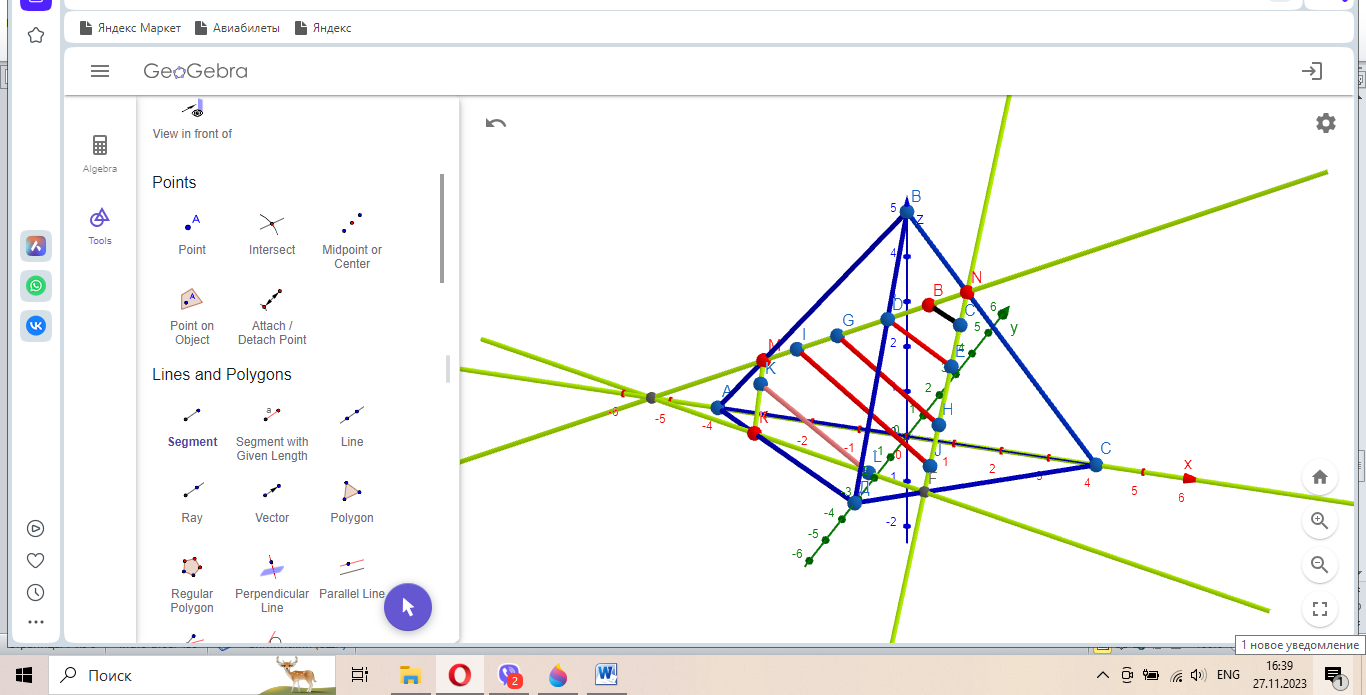
V. Закрепление знаний.

Каждая группа работает над индивидуальным проектом в динамической среде GeoGebra. Задание для групп:

VI. Рефлексия.

Все молодцы, всем отлично! Все справились с не очень легкой задачей. Понравился вам урок? Интересно было? Изучать динамическую математику гораздо интереснее и полезнее, не правда ли? А теперь задание на дом.

VII. Домашнее задание Выполнить индивидуальный проект «Постоение сечений в среде GeoGebra».