Обобщающий урок по теме «Геометрическая прогрессия»
Цели:
Образовательные
- Обобщить знания обучающихся по теме: «Геометрическая прогрессия»; закрепить навыки использования теоретического материала при решении задач; разобрать типичные задания, встречающиеся для подготовки к ГИА.
Развивающая
- Развивать познавательный интерес обучающихся, умение логически мыслить; учить их видеть связь между математикой и окружающей жизнью.
Воспитательная
Формировать у обучающихся наблюдательность и творческую активность; воспитывать самостоятельность, аккуратность, четкость в действиях.
I.Организационный момент (У. приветствует детей)
- Я бы хотела начать урок цитатой Георга Гегеля(Слайд 1)
Не в количестве знаний заключается
образование, а в полном понимании
и искусном применении всего того,
что знаешь.
Георг Гегель
- Эти слова, сказанные немецким философом несколько столетий назад, актуальны и сегодня.
II. Актуализация знаний.
(Слайд 2)
- На слайде записаны несколько последовательностей:
1) 2;-6;18;-54;…;
2) 625;125;25;5;…;
3)-1;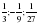 ;…;
;…;
- Какую закономерность вы заметили?
(1. Каждый член последовательностиначиная со второго равен предыдущему члену, умноженному на -3
2. Каждый член последовательностиначиная со второго равен предыдущему члену, умноженному на
3. Каждый член последовательностиначиная со второго равен предыдущему члену, умноженному на - 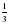 ).
).
- Как называются такие последовательности? (геометр.прогрессия)
- Сформулируйте тему нашего урока.(Геометрическая прогрессия)
– Откройте тетради, запишите число –…..классная работа. (слайд 3)
тему урока «Геометрическая прогрессия»
- Какие поставить цели и решить задачи нам предстоит?
(Повторить и закрепить формулы геометрической прогрессии, учиться применять формулы при решении задач)
- Что вы знаете о геометрической прогрессии?
(Последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число)
- Что умеете находить?
(n-ый член, знаменатель, сумму первых n-членов геометрической прогрессии)
ΙΙΙ. Работа в группах
Так как вы повторяли теоретический материал по теме «Геометрическая прогрессия», то предлагаю вам проверить знания теории по данной теме, выполнив следующую работу в группе:
(слайд 4)
- составить кластер,
- выбрать верные утверждения в тесте,
- ответить на вопрос «истинно» или «ложно» данное утверждение, аргументировав ответ.
(слайд 4)
- Группа, которая составляла кластер размещайте его на доске.
- Группа, которая выполняла тест, какое ключевое слово у вас получилось?
- И группы, которые отвечали на вопрос«Истинно или ложно?»
Какие утверждения у вас верны?
С какими вы не согласны и что нужно исправить?
Применение геометрической прогрессии при решении текстовых задач
-Повторив определение и формулы геометрической прогрессии можно решить много интересных задач. У вас на партах карточки с условием. Решаете в парах. Решение защищаете у доски ( записывают его маркером на А4)
(Работа в парах . Раздаются каждой паре карточки с задачами.
Ученики решают задачи в тетради, а затем у доски защищают их ( объясняют ход решения).
(слайд 6)
На опытном участке леса ежегодный прирост древесины составляет 10%. Какое количество древесины будет на этом участке через 5 лет, если первоначальное количество древесины равно 20 000м3? (16105,1 м3)
Решение:первоначальное количество древесины равно 20 000м3. Через год кол-во древесины возрастет на 10% и составит 110% от 20 000м3, т.е. будет равно
20 000·1,1 м3. Через 2 года кол-во древесины составит
(20 000·1,1)·1,1=20 000·1,12м3. Через 3 года 20 000·1,13 м3 и т.д..Т.О. мы имеем дело с геометрической прогрессией: 20 000;20 000·1,1; 20 000·1,13; …; Поэтому количество древесины через 5 лет будет равно шестому члену этой прогрессии, т.е. составит 20 000·1,15=16105,1 м3.
2. Задание 13 № 99586. Бизнесмен Бубликов получил в 2000 году прибыль в размере 5000 рублей. Каждый следующий год его прибыль увеличивалась на 300% по сравнению с предыдущим годом. Сколько рублей заработал Бубликов за 2003 год?
Решение.
Бизнесмен Бубликов получил в 2000 году прибыль в размере 5000 рублей. Каждый следующий год его прибыль увеличивалась на 300%, то есть каждый год составляла 400% . Это в 4 раза больше, по сравнению с предыдущим годом. Мы имеем дело с геометрической прогрессией:в1= 5000;q=4; Найти в4.
Чтобы ответить на вопрос задачи, нужно найти четвертый член геометрической прогрессии. За 2003 год Бубликов заработал
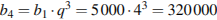 рублей.
рублей.
Ответ: 320000.
(слайд 7)
Клиент взял в банке кредит в размере 500 000 рублей на 3 года под 20% годовых. Какую сумму клиент должен вернуть банку в конце срока? (864000)
Решение: Через год долг перед банком возрастет на 20% и составит 120% от
500 000р., т.е. будет равным 500 000·1,2. Через 2 года долг станет 500 000·1,22. Через 3 года должен вернуть банку 500 000·1,23=864 000р..
Найдите сумму первых шести членов геометрической прогрессии, первый член которой равен 2, а пятый равен 162, если известно, что ее члены с нечетными номерами положительны, а с четными отрицательны.
Геометрическая прогрессия в ОГЭ.
Скоро сдача государственных экзаменов. Вы уже готовитесь и обратили внимание на то, что геометрическая прогрессия есть в тренировочных вариантах ОГЭ. Сейчас вы выполните самостоятельную работу, задания которой взяты из открытого банка и сборников для подготовки к ОГЭ.
- подпишите бланки ответов и укажите вариант
- решаете в тетрадях, ответ вписываете в бланк ответов
- Собрать бланки ответов
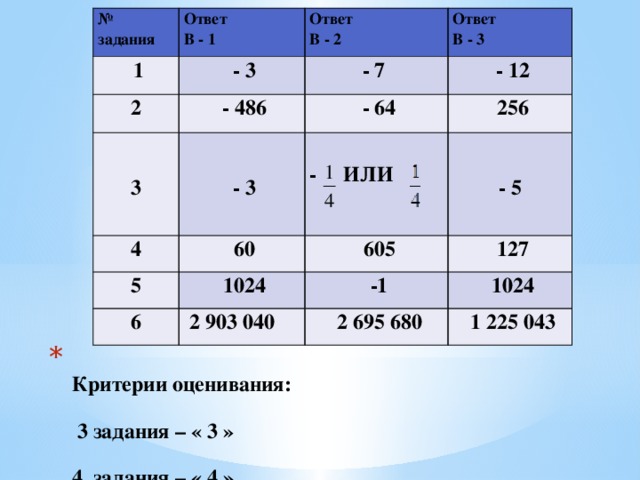
(слайд8) - Проверим с.р.
В-1
| Ф.И. - |
|
|
| № задания | Ответ В - 1 | Ответ В - 2 | Ответ В - 3 |
| 1 |
|
|
|
| 2 |
|
|
|
| 3 |
|
|
|
| 4 |
|
|
|
| 5 |
|
|
|
| 6 |
|
|
|
Критерии оценивания:
3 задания – « 3 »
4 задания – « 4 »
5-6 заданий – « 5 »
– Итак, сегодня на уроке мы:
1. Повторили… (опред.Геом. Прогр., формулы н-го члена, знаменателя, формулы суммы первых н-членов геом.пр.)
2. Узнали…(что формулу н го члена можно применять при банковских расчетах, в лесничестве )
3. Закрепили… (знание формул и практическое их применение)
– Что на уроке понравилось? (работать в группе, в паре, решать задачи на банковские расчеты)
– С какими трудностями столкнулись? (Считать сложные проценты)
– Где в жизни могут пригодиться знания по данной теме?(работая в банке, лесничестве, обращаясь в банк за кредитом или делая вклад)
- д/з №656,№701,В-19(№6) из сборника подготовки к ОГЭ.
– Хочется закончить урок лозунгом многих математиков XVII века:
( Слайд9 )
«Двигайтесь вперед, и вера в правильность результатов к вам придет!»
– Спасибо за урок.






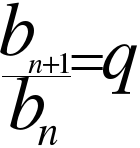
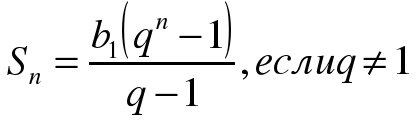
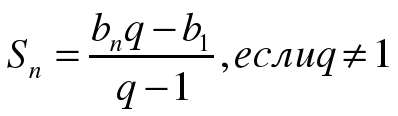

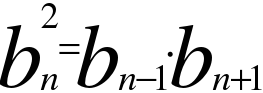
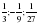 ;…;
;…;
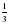 ).
).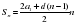
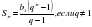
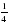 ;1;4;… .Найдите произведение первых пяти ее членов.
;1;4;… .Найдите произведение первых пяти ее членов.