Урок-игра по теме: «Решение простейших тригонометрических уравнений»

«Пик знаний»

Урок-игра по теме: « Решение простейших тригонометрических уравнений»11 класс Выполнил учитель математики ГКОУ СОШ № 4 при ИУ Овсянников Е.М. 2024г.

Учиться можно только весело…

Чтобы переваривать

знания, надо поглощать

их с аппетитом.

Анатоль Франс

1844 - 1924

Тема урока:

Решение простейших тригонометрических уравнений

Цель урока:

Повторить тригонометрические формулы и способы решения простейших тригонометрических уравнений

«Кто смолоду делает и думает сам, тот становится потом надёжнее, крепче, умнее»

В . Шукшин

1этап. Разминка: какие из формул записаны неверно?

1) =1

2)

3) = а, х = arccos a +2

4)

5) tg x = a, x=arctg a +2

6) Cos 2x =

Математика – самый короткий путь к самостоятельному мышлению

В.КАВЕРИН

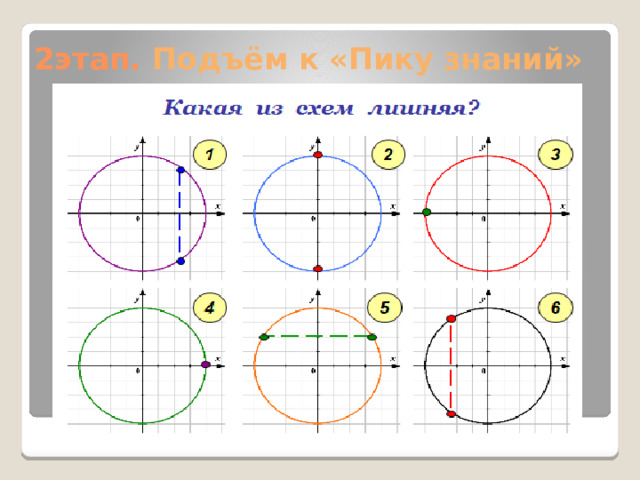
2этап. Подъём к «Пику знаний»

Ответ:

• 5 – я схема лишняя, так как эта схема изображает решение уравнения вида sin x=a ;
• 1, 2, 3, 4, 6 – изображают решение уравнений вида Cosx=a .

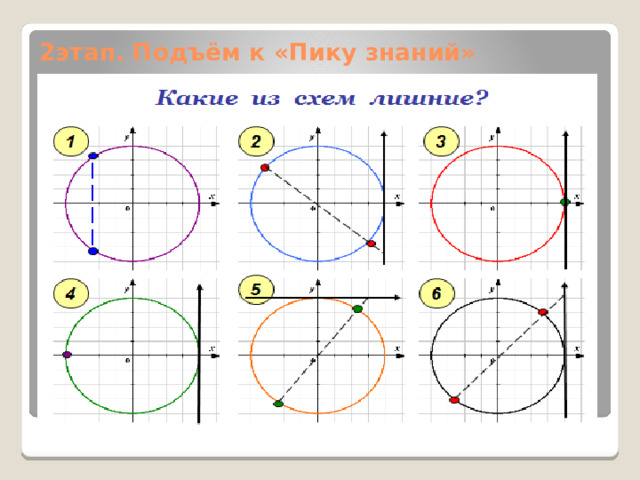
2этап. Подъём к «Пику знаний»

Ответ:

• 1 – я схема лишняя, так как она изображает решение уравнения вида cosx=a;
• 5 – я схема лишняя, так как эта схема изображает решение уравнения вида ctgx=a ;
• 2, 3, 4, 6 – изображают решение уравнений вида tgx=a .

Установите соответствие:

Молодцы!

1

sin x = 0

cos x = -1

2

sin x = 1

3

4

cos x = 1

tg x = 1

5

sin x = - 1

6

7

cos x = 0

3этап. Подъём к «Пику знаний»

1группа: знаю

2группа: прав

3группа: умею

Из истории развития тригонометрии

Что такое тригонометрия?

ТРИГОНОМЕТРИЯ – (от греч . trigwnon – треугольник и metrew – измеряю) – математическая дисциплина, изучающая зависимости между углами и сторонами треугольников и тригонометрических функций.

Исследования в области тригонометрии:

• в Древнем Вавилоне;
• в Древнем Вавилоне;

• в Древней Греции;
• в Древней Греции;

• на Ближнем и Среднем востоке;
• на Ближнем и Среднем востоке;

• в западной Европе .
• в западной Европе .

• Современная тригонометрия
• Современная тригонометрия

в Древнем Вавилоне;

в Древнем Вавилоне

А начиналось все очень давно. Первые отрывочные сведения по тригонометрии сохранились на клинописных табличках Древнего Вавилона. Астрономы Междуречья научились предсказывать положение Земли и Солнца и именно от них к нам пришла система измерения углов в градусах, минутах и секундах, потому что у вавилонян была принята шестидесятеричная система счисления.

в Древней Греции;

в Древней Греции

Однако первые по-настоящему важные достижения принадлежат древнегреческим ученым.

Птолемей

Евклид

Гиппарх

на Ближнем и Среднем востоке

на Ближнем и Среднем востоке

Термины «синус» и «косинус» пришли от индийцев, не обошлось и без любопытного недоразумения. Полухорду индийцы называли «ардхаджива» (в переводе с санскрита – «половина тетивы лука»), а потом сократили это слово до «джива». Мусульманские астрономы и математики, получившие знания по тригонометрии от индийцев, восприняли его как «джиба», а затем оно превратилось в «джайб», что на арабском языке означает «выпуклость», «пазуха». Наконец, в 7 в. «джайб» буквально перевели на латынь словом «sinus», которое не имело никакого отношения к обозначаемому им понятию.

в западной Европе.

в западной Европе

Дальнейшее развитие тригонометрии шло по пути накопления и систематизации формул, уточнения основных понятий, становления терминологии и обозначений. Многие европейские математики работали в области тригонометрии. Среди них такие великие ученые, как Николай Коперник (1473–1543),

Тихо Браге (1546–1601) и Иоганн Кеплер (1571–1630),

Исаак Ньютон (1643–1727),

Леонард Эйлер (1707–1783),

Франсуа Виет

(1540–1603)

Современная тригонометрия

К концу 18 в. тригонометрия как наука уже сложилась. Тригонометрические функции нашли применение в математическом анализе, физике, химии, технике – везде, где приходится иметь дело с периодическими процессами и колебаниями – будь то акустика, оптика или качание маятника .

5 этап. Подъём к «Пику знаний»

«Счастливая случайность выпадает лишь на долю подготовленных умов»

( Луи Пастер )

Отвечать только «Да» и «Нет»

• Sin 2 х + cos 2 x = 1 – основное тригонометрическое тождество.
• Тригонометрия – раздел геометрии.
• сos x , Sinх, tgx, сtgx – тригонометрические функции.
• [-1; 1] – область значения функций Sinх и сos x.

• [ ] – область определения функции tgx.
• ( - ∞;∞ ) – область значения функции сtgx.

• Сtgx =
• 8. Математика – мой любимый предмет

6 этап . Решить кроссворд

Кроссворд  ( англ.   Crossword  — пересечение слов или  крестословица  ) — самая распространённая в мире  игра  , состоящая в разгадывании слов по определениям.

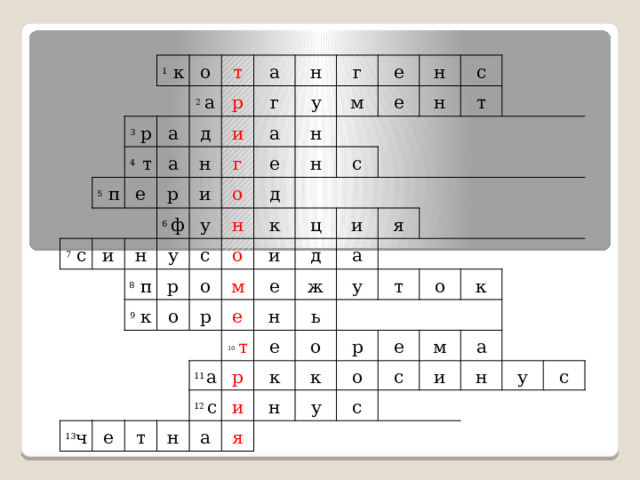
1 к

о

3 р

4 т

2 а

5 п

а

т

е

7 с

а

р

а

д

р

н

и

и

н

г

г

а

н

у

г

6 ф

и

е

8 п

у

о

н

у

е

м

9 к

р

д

н

н

е

с

н

о

о

о

к

с

с

н

13 ч

м

ц

и

р

т

д

е

е

е

и

11 а

т

10 т

н

я

ж

а

12 с

ь

н

е

у

р

о

а

т

к

и

н

р

я

к

о

о

у

е

к

с

с

м

и

а

н

у

с

Домашнее задание

• sin 2 2x + cos 4x = 0

• сos6xcos5x + sin6xsin5x = - 1

Спасибо за урок