Урок-презентация "Двугранный угол"

ДВУГРАННЫЙ УГОЛ

Урок геометрии в 10 классе.

Учитель: Кречетов А.Н.

Планиметрия

Стереометрия

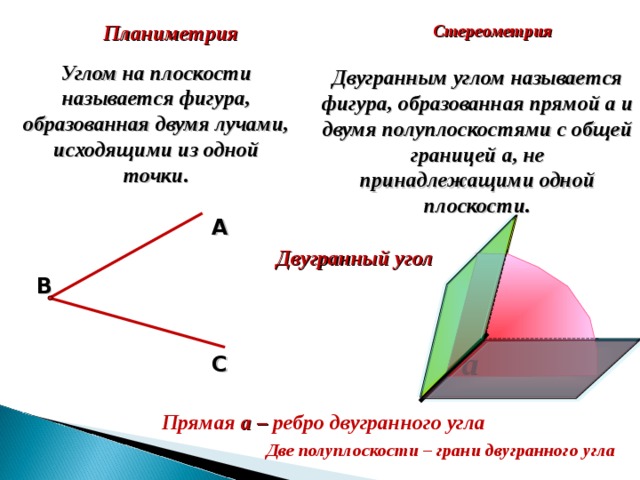
Углом на плоскости называется фигура, образованная двумя лучами, исходящими из одной точки.

Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с общей границей a , не принадлежащими одной плоскости.

А

Двугранный угол

В

а

С

Прямая a – ребро двугранного угла

Две полуплоскости – грани двугранного угла

2

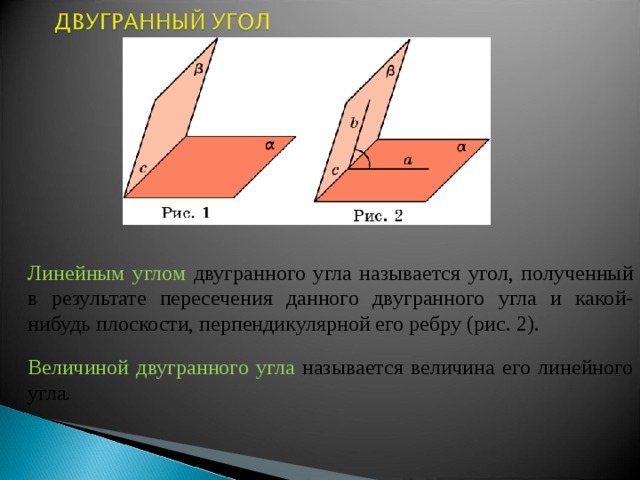
Линейным углом двугранного угла называется угол, полученный в результате пересечения данного двугранного угла и какой-нибудь плоскости, перпендикулярной его ребру (рис. 2).

В режиме слайдов ответ появляется после кликанья мышкой.

Величиной двугранного угла называется величина его линейного угла.

2

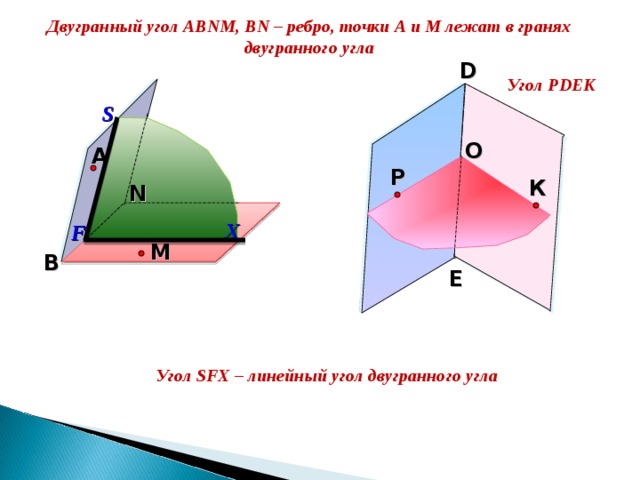
Двугранный угол АВ N М, В N – ребро, точки А и М лежат в гранях двугранного угла

D

Угол Р DEK

S

O

А

Р

К

N

X

F

M

В

E

Угол SFX – линейный угол двугранного угла

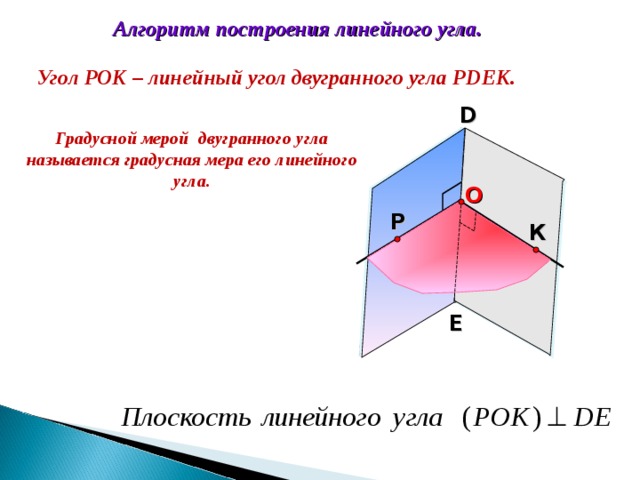
Алгоритм построения линейного угла.

Угол РОК – линейный угол двугранного угла Р DE К.

D

Градусной мерой двугранного угла называется градусная мера его линейного угла.

O

Р

К

E

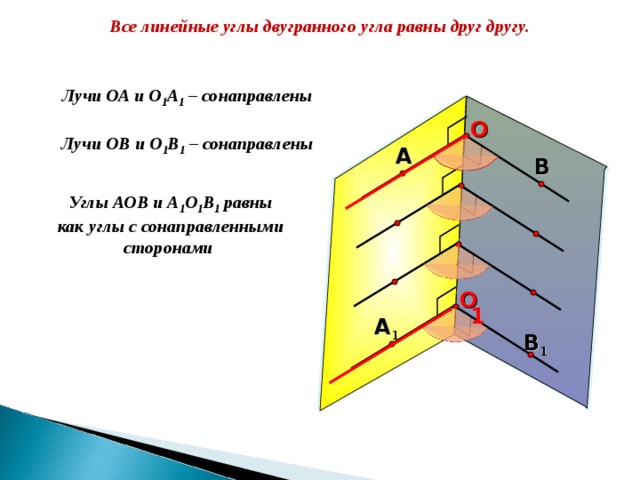
Все линейные углы двугранного угла равны друг другу.

Лучи ОА и О 1 А 1 – сонаправлены

O

Лучи ОВ и О 1 В 1 – сонаправлены

А

В

Углы АОВ и А 1 О 1 В 1 равны

как углы с сонаправленными сторонами

O

1

А 1

В 1

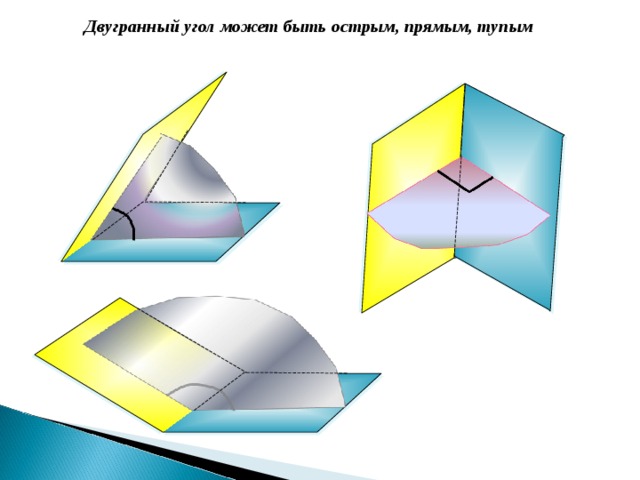
Двугранный угол может быть острым, прямым, тупым

Н-я

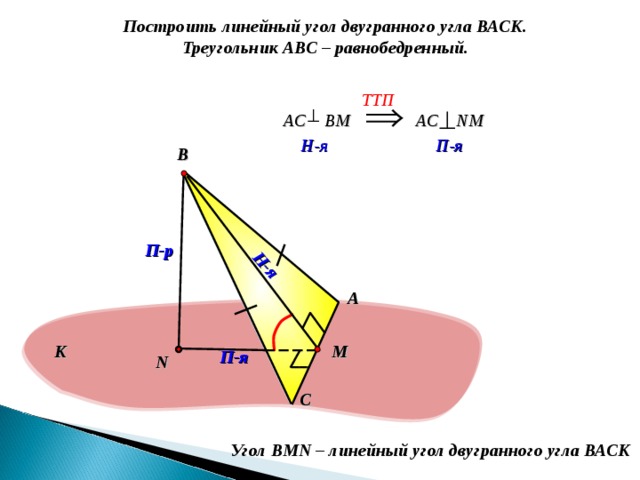
Построить линейный угол двугранного угла ВАСК.

Треугольник АВС – равнобедренный.

TT П

АС ВМ

АС N М

П-я

H -я

В

П-р

А

К

M

П-я

N

С

Угол В MN – линейный угол двугранного угла ВАСК

8

Н-я

П-я

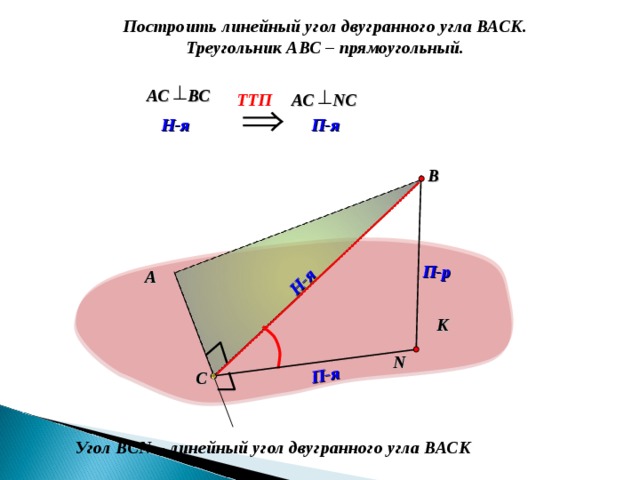
Построить линейный угол двугранного угла ВАСК.

Треугольник АВС – прямоугольный.

АС ВС

TT П

АС N С

П-я

H -я

В

П-р

А

К

N

С

Угол ВС N – линейный угол двугранного угла ВАСК

9

Н-я

П-я

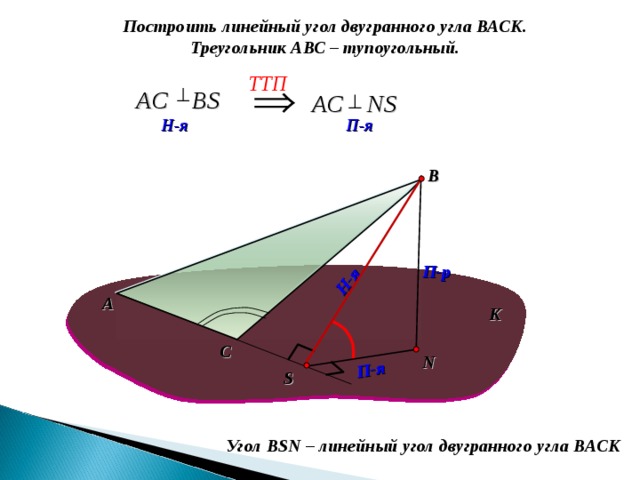
Построить линейный угол двугранного угла ВАСК.

Треугольник АВС – тупоугольный.

TT П

АС В S

АС NS

П-я

H -я

В

П-р

А

К

С

N

S

Угол В SN – линейный угол двугранного угла ВАСК

10

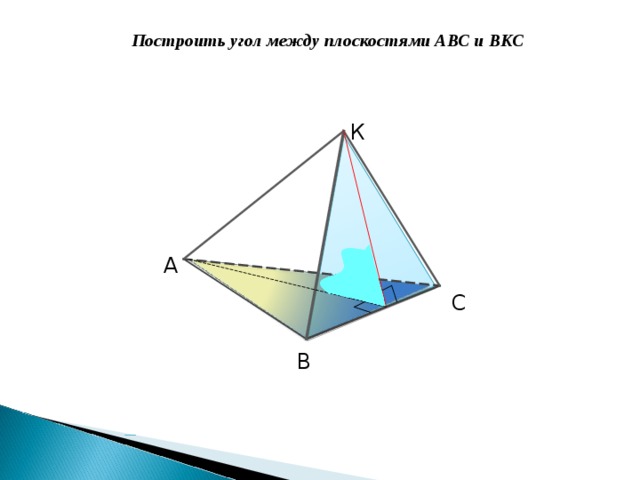
Построить угол между плоскостями АВС и ВКС

К

А

С

В

11

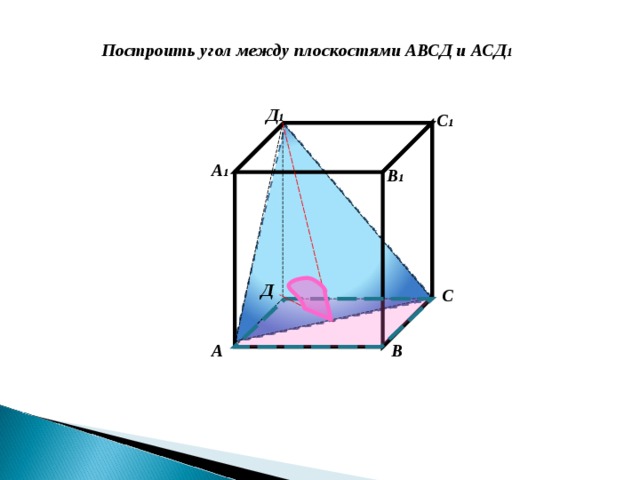
Построить угол между плоскостями АВСД и АСД 1

Д 1

С 1

А 1

В 1

Д

С

А

В

В кубе A … D 1 найдите уг ол между плоскостями

ABC и CDD 1 .

Ответ: 90 o .

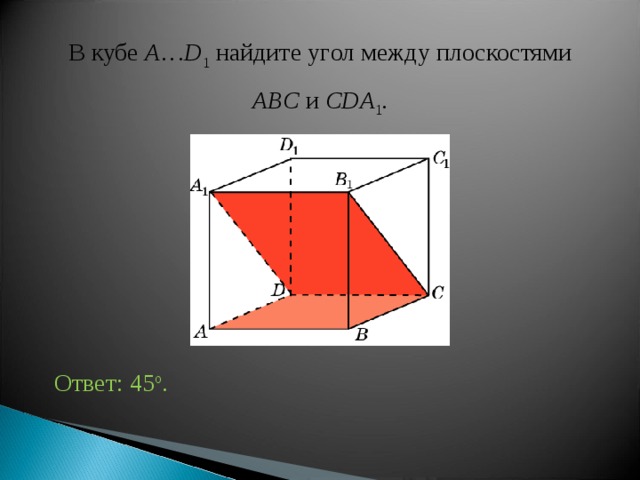
В кубе A … D 1 найдите уг ол между плоскостями

ABC и CDA 1 .

Ответ: 45 o .

В кубе A … D 1 найдите уг ол между плоскостями

ABC и BDD 1 .

Ответ: 90 o .

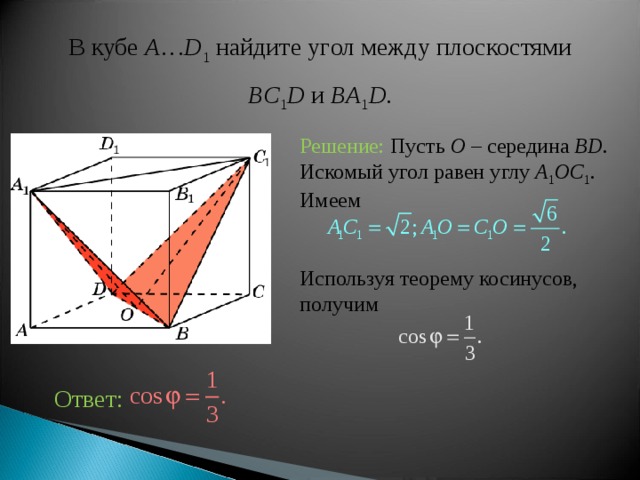
В кубе A … D 1 найдите уг ол между плоскостями

BC 1 D и BA 1 D .

Решение: Пусть O – середина BD . Искомый угол равен углу A 1 OC 1 . Имеем

Используя теорему косинусов, получим

Ответ:

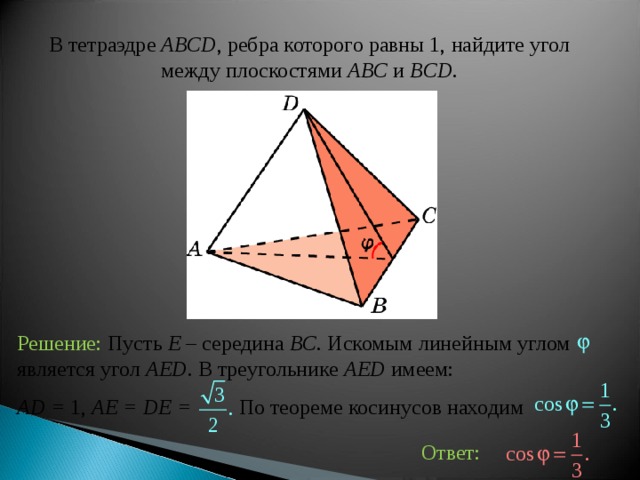
В тетраэдре ABCD , ребра которого равны 1, найдите угол между плоскост ями ABC и BCD .

Решение: Пусть E – середина BC . Искомым линейным углом является угол AED . В треугольнике AED имеем:

AD = 1, AE = DE = По теореме косинусов находим

Ответ:

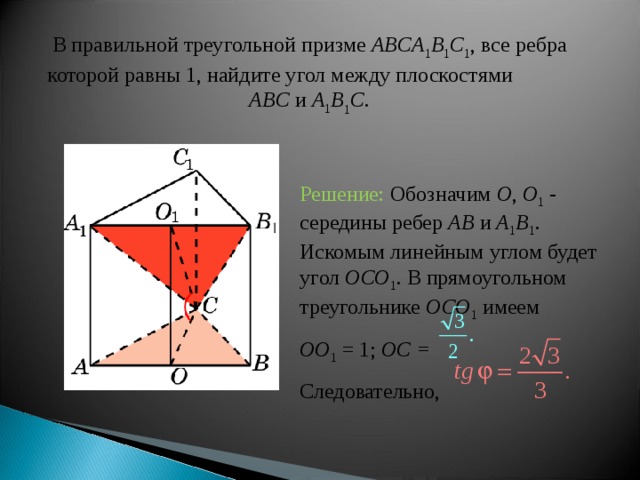
В правильной треугольной призме ABCA 1 B 1 C 1 , все ребра которой равны 1, найдите угол между плоскост ями ABC и A 1 B 1 C .

Решение: Обозначим O , O 1 - середины ребер AB и A 1 B 1 . Искомым линейным углом будет угол OCO 1 . В прямоугольном треугольнике OCO 1 имеем

OO 1 = 1; OC =

Следовательно,

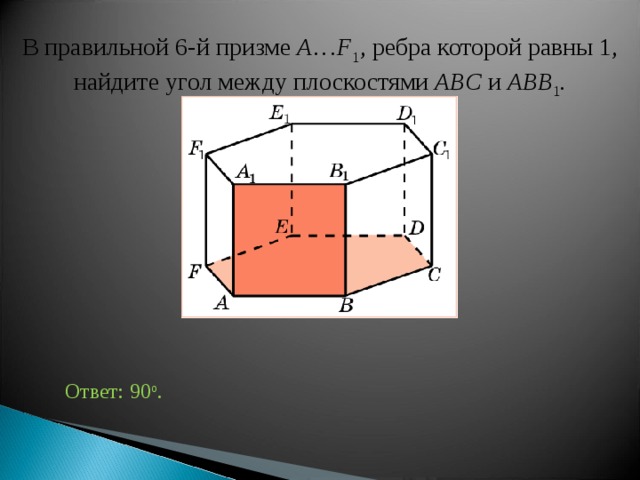
В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите у гол между плоскостями ABC и ABB 1 .

Ответ: 90 о .

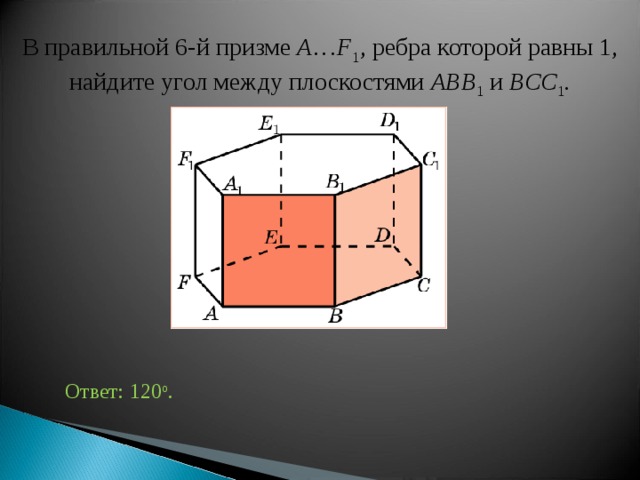
В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите у гол между плоскостями ABB 1 и BCC 1 .

Ответ: 120 о .

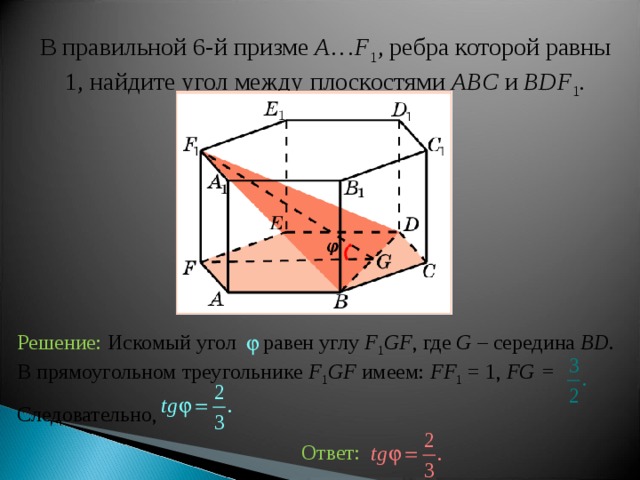
В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите у гол между плоскостями ABC и BDF 1 .

Решение: Искомый угол равен углу F 1 GF , где G – середина BD . В прямоугольном треугольнике F 1 GF имеем: FF 1 = 1, FG =

Следовательно,

Ответ:

Закрепление:

• Какой угол в пространстве называется двугранным углом?
• Что называется линейным углом двугранного угла?
• Чему равна градусная мера двугранного угла?
• Как найти величину двугранного угла?

Домашнее задание:

с. 47, п.22

№ 167