Урок Прикладные задачи, связанные с квадратичной функцией.
Дополнительный материал (можно рассмотреть на уроке или факультативном занятии).
«Стоя на одном месте,
новых горизонтов не откроешь»
(поговорка)
Цель урока:
1.Развитие межпредметых связей.
2.Способствовать умению переноса знаний в новую ситуацию.
3.Развитие творческих способностей учащихся.
Ход урока:
1. Парабола, как огибающая.
2. Парабола, как нитка с бусинками.
3. Вышивание параболы.
4. Парабола, как след карандаша
5. Полет стрелы.
6. Задача о зеркале прожектора.
7.Примеры зависимостей, выражающихся квадратичной функцией.
Другие способы получения параболы. Дополнительный материал
Учитель: Получить график квадратичной функции – параболу можно и другими способами. 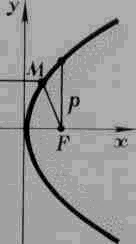
Учитель: Параболу можно определить как кривую, состоящую из всех точек М плоскости, одинаково удалённых от заданной точки – фокуса параболы – и от заданной прямой – директрисы. Такое определение параболы наводит на идею создания чертёжного прибора, способного вычерчивать параболу. Прибор состоит из линейки и угольника, к одному из острых углов которого прикреплена нить, по длине равная прилегающему к этому углу катету-I. Другой конец нити закрепляется в точке плоскости – фокусе параболы, линейка прикладывается к директрисе, угольник скользит катетом-II по линейке, а карандаш (мел) удерживает нить в натянутом состоянии и прижимается к катету-I, скользя вдоль него. При движении угольника вдоль линейки карандаш (мел) вычерчивает параболу. (Учитель демонстрирует получение параболы с помощью модели, изготовленной из линейки, угольника, нити).
Учитель: Легко получить параболу с помощью обычного карманного фонарика. (Учитель демонстрирует получение кривых с помощью фонарика, экрана). Световое пятно от вертикально расположенного фонаря будет кругом. Немного повернём его, и пятно будет иметь форму овала. Такой овал называется эллипсом. При дальнейшем повороте фонарика эллипс будет всё больше и больше вытягиваться, а в некоторый момент его наиболее удалённая точка уйдёт в бесконечность. Кривая, ограничивающая такое пятно, называется параболой. Неограниченные кривые, которые получаются при дальнейшем вращении фонарика, называются гиперболами. Все получившиеся кривые – окружность, эллипс, парабола, гипербола – конические сечения. Такое название они получили заслуженно, поскольку световой столб, выходящий из фонарика, является конусом.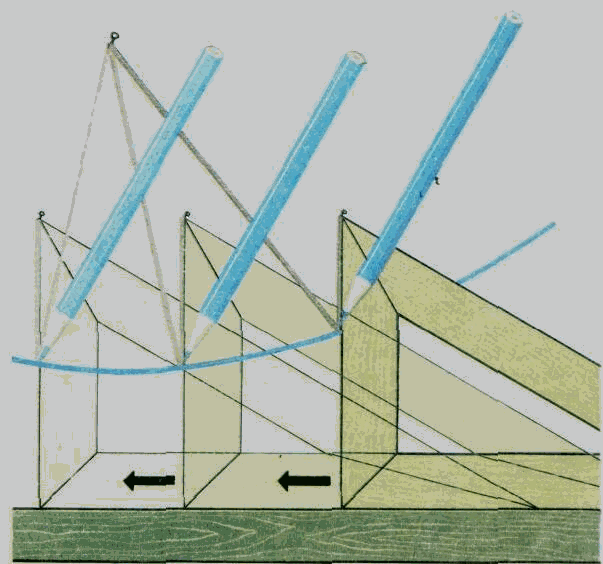
Парабола, как огибающая.
Параболу можно рассматривать, как огибающую семейства прямых. Можно показать миниатюру «Парабола, как огибающая» (см. сайт www.etudes.ru ) Выполним следующие задания:
1.Возьмем прямоугольный лист бумаги, отметим точку А на нем и будем сгибать лист таким образом, чтобы нижний край проходил через точку А (рис.1).
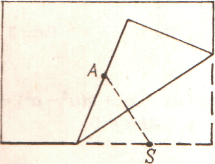 рис.1
рис.1
Отметим на наложенном нижнем крае точку, совпадающую с А, и. развернув лист, получим точку S, являющуюся следом точки А на нижнем крае.
Произведя много сгибаний и расправляя каждый раз лист, получим много следов S, S, S, … на нижнем крае и столько же линий сгиба m, m, m, …(рис. 2).
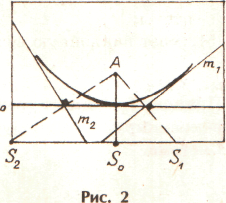
Рис.2
При внимательном рассмотрении листа можно разглядеть область на листе, через точки которой не проходят линии сгиба. Эта область содержит точку А и ограничена некоторой кривой, которая называется огибающее, каждая линия сгиба касается огибающей в некоторой точке. Огибающая является параболой.
2. Рассмотрим угол с вершиной О и сторонами n и m. На сторонах угла отметим две фиксированные точки N и M соответственно, равноудаленные от вершины угла О. На сторонах n и m рассмотрим соответствующие последовательности точек N, N, N, … и M, M, M, …, при чем MM = NN и точки M и N расположены по разные стороны от прямой MN
Перегибая угол по прямым MN и разгибая, получим следы сгибов. Рассмотренное семейство прямых имеет огибающую, являющуюся параболой.
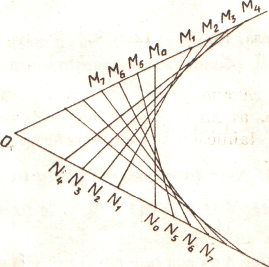 Рис.4
Рис.4
3. Огибающая и оптическое свойство. Рассмотрим огибающую (т.е. параболу) для некоторого однопараметрического семейства линий сгиба. Пусть произвольная прямая m касается параболы в точке М, H – проекция точки М на нижний край k и S – след точки А на нижнем крае (рис. 5).
Тогда AM = HM по свойству параболы, AM = MS по свойству серединного перпендикуляра.
Длина наклонной MS равна длине перпендикуляра MH, следовательно, S совпадает с H. Поэтому отрезки AM и HM образуют с касательной равные углы, при чем HM перпендикулярно краю k.
Если в точке М установить зеркало вдоль касательной и обращенное отражающей поверхностью к параболе, то световой луч АМ после отражения в точке М пойдет вдоль луча HM. Следовательно, все лучи выходящие из фокуса А, после отражения, 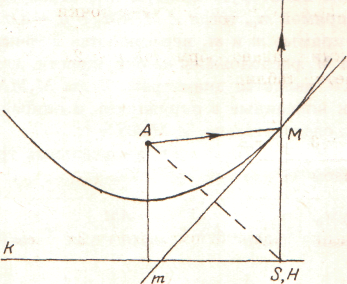 Рис.5
Рис.5
от параболического зеркала пойдут в одном и том же направлении, перпендикулярном краю k, т.е. перпендикулярно директрисе k (рис.5).
Парабола как нитка с бусинками
Начертите прямую d и на расстоянии р от нее отметьте точку F (рис. 6).
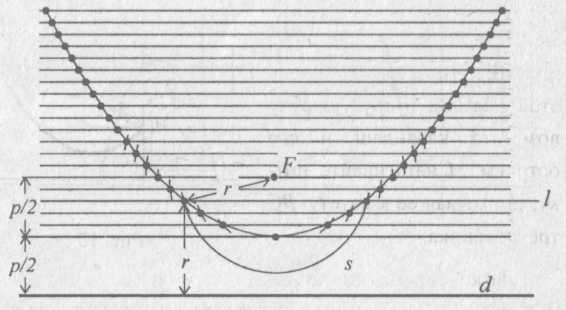
Рис. 6.
Выберите достаточно много чисел r, удовлетворяющих р неравенству 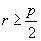
Для каждого выбранного числа r проведите параллельно прямой d прямую l, удаленную от d на расстояние r.
Опишите дугу s радиуса r с центром в точке F.
Точки пересечения построенных прямых l и соответствующих дуг s будут (как бусинки на нитку) нанизываться на параболу, поскольку они находятся на одинаковом расстоянии от фокуса F и директрисы d параболы.
Вышивание параболы
На листе плотной бумаги начертите прямую m и перпендикуляр FA к ней (рис. 7).
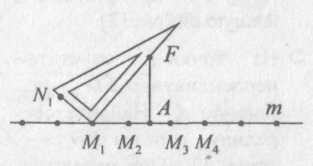
Рис. 7.
На прямой m, по обе стороны от точки А, выберите произвольно несколько точек М1, М2, … Мn.
Приложите прямоугольный треугольник так, чтобы вершина прямого угла совпала с точкой М1, один катет прошел через точку F и весь треугольник расположился выше прямой m.
На другом катете отметьте точку N1.
Точно так же постройте еще точки N1, N2, Nn.
Возьмите иглу с цветной ниткой, завяжите на нитке узелок, проткните с обратной стороны лист бумаги в точке М1 и соедините стежком точку М1 с точкой N1, потом точно так же — точку М2 с точкой N2, точку М3 с точкой N3, и так далее.
Вы заметили, что все нитки сгущаются (можно сказать, скапливаются) вокруг одной и той же кривой? "Увиделась" ли вам в этой кривой парабола?
Парабола как след карандаша
На листе плотной бумаги проведите прямую d, которая станет директрисой будущей параболы.
Выберите точку F (фокус параболы) вне этой прямой и воткните в нее булавку.
Чтобы вам легче было ориентироваться, обозначьте вершины используемого далее чертежного прямоугольного треугольника буквами А, В, С. Один конец нити, длина которой равна катету ВС, привяжите к булавке F, другой конец закрепите кнопкой в вершине В треугольника (рис. 8).
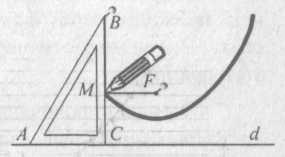
Рис. 8.
Теперь вам предстоит довольно непростая работа: приложите катет АС к прямой d и одной рукой передвигайте треугольник вдоль этой прямой; в другую руку возьмите карандаш и его острием М натягивайте нитку, прижимая ее к катету ВС треугольника.
Легко видеть, что отрезки MF и МС равны и, следовательно, острие М карандаша описывает параболу. Кропотливо? Да, но красиво!
Лабораторная работа. (Дополнительный материал для сильных учащихся)
1.Подготовьте набор принадлежностей для построения параболы. Для заданных фокуса и директрисы постройте соответствующую им параболу.
2.Расстояние от фокуса параболы до директрисы равно 4 см. Чему равно наименьшее расстояние от точек на параболе до директрисы? Укажите соответствующую точку на параболе.
3.Для параболы с заданным фокусом и директрисой проведите касательную, перпендикулярную оси параболы.
4.Что будет происходить с параболой. Если фокус: а) приближается к директрисе; б) удаляется от директрисы?
5. Для параболы с заданным фокусом и директрисой проведите касательную, проходящую через данную точку: а) на параболе; б) вне параболы.
Докажите, что две касательные к параболе, проведенные из точки, принадлежащей директрисе, перпендикулярны.
7.Для заданных фокуса и директрисы параболы с помощью циркуля и линейки постройте несколько точек параболы.
8.Даны фокус параболы и две касательные. Постройте директрису этой параболы.
9. Даны фокус, касательная и на ней точка касания. Постройте директрису параболы.
10.Даны директриса и две касательные. Постройте фокус параболы.
11. Даны директриса, касательная и на ней точка касания. Постройте фокус параболы.
12.Даны две пересекающиеся прямые. Нарисуйте какую-нибудь параболу, касающуюся этих прямых. Сколько таких прямых? Какие точки плоскости могут быть фокусами этих парабол?
13.Дана парабола. Укажите способ нахождения ее фокуса и директрисы.
Показать миниатюру «Оптические свойства параболы» (см. сайт www.etudes.ru ).
Задача.
Построй те график функции у = х². Масштаб возьмите покрупней: 1=2см( 4 клетки). Отметьте на оси оу точку F (0, 1/4). Полоской бумаги измерьте расстояние от точки F до какой-нибудь точки М параболы. Затем приколите полоску в точке М и поверните ее вокруг этой точки так, чтобы она стала вертикальной. Конец полоски опустится немного ниже оси абсцисс. Отметьте на полоске, на сколько она выйдет за ось абсцисс (рис. 4). Возьмите теперь другую точку на параболе и повторите измерение еще раз. На сколько теперь опустился конец полоски за ось абсцисс?
Результат я могу вам сказать заранее: какую бы точку на параболе у = х² вы ни взяли, расстояние от этой точки до точки (0;1/4) будет больше расстояния от той же точки до оси абсцисс всегда на одно и то же число – на 1/4.
Можно сказать иначе: расстояние от любой точки параболы у = х² до точки (0;1/4) равно расстоянию от той же точки параболы до прямой у = - 1/4, параллельной оси ох.
Эта замечательная точка F (0;1/4) называется фокусом параболы у = х², а прямая
у = - 1/4- директрисой этой параболы. Директриса и фокус есть у всякой параболы.
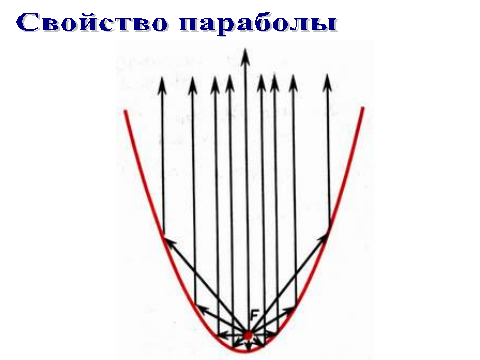
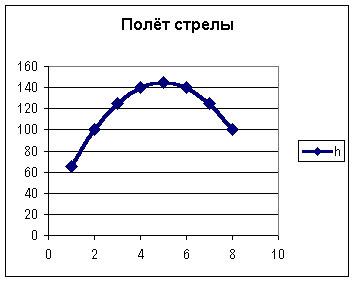
Задача Полет стрелы
С башни выпустили вверх стрелу из лука. Если начальная скорость стрелы равна 50 м/с, высота башни 20 м и t – время полёта стрелы (в секундах), то расстояние h (в метрах) стрелы от поверхности земли можно найти по формуле h=-5t2+50t+20 (приближённое значение ускорения свободного падения считается равным с 10 м/с2). Какой наибольшей высоты достигнет стрела? Постройте график движения стрелы по уравнению h= -5t2 +50t+20. Значение t[1;8] c шагом 1. Отметьте точку, в которой стрела достигнет наибольшей высоты.
Задача о зеркале прожектора
Знакомство с новым классом математических задач опять начнем с нескольких простых примеров. Мы уже встречали дифференциальные уравнения. Данный пример будет связан с определением формы зеркала прожектора. Соответствующую задачу сформулируем следующим образом: найти такую форму зеркала, чтобы лучи от точечного источника света после отражения в нем образовывали параллельный пучок.
Из соображений симметрии ясно, что поверхность зеркала должна быть поверхностью вращения с осью, проходящей через источник света параллельно отраженным лучам. Проведем через ось какую-нибудь плоскость и рассмотрим сечение нашего зеркала этой плоскостью. Введем в ней систему координат х, у. Начало координат О совместим с источником света, а ось у направим параллельно отраженным лучам (см. рис.3). Уравнение линии пересечения данной плоскости с зеркалом запишется в виде у = φ (х). Наша задача заключается в том, чтобы найти функцию φ(х), определяющую форму зеркала.
Рассмотрим рис.4. Пусть М — произвольная точка искомой линии, ее координаты (х, у), NQ— касательная к линии в точке М, N — точка пересечения касательной с осью у. Луч света, выходящий из точки О, после отражения от зеркала в точке М должен идти параллельно оси у. Согласно закону отражения 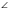 ОМN =
ОМN = 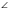 РМQ. С другой стороны,
РМQ. С другой стороны,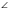 ОNМ=
ОNМ=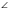 РМQ, как соответственные при параллельных прямых. Таким образом, в треугольнике ОМN углы в вершинах М и N равны, т. е. этот треугольник равнобедренный. В результате будем иметь:
РМQ, как соответственные при параллельных прямых. Таким образом, в треугольнике ОМN углы в вершинах М и N равны, т. е. этот треугольник равнобедренный. В результате будем иметь:
ОN = ОМ = 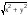
Теперь рассмотрим ΔКМN и подсчитаем тангенс угла КМN, равного углу α:
tg α = KN/KM = (KO + ON)/KM.
Таким образом, tg α = (у + 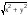 )/х = х/(
)/х = х/(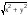 – у). (1)
– у). (1)
Угол α определяет наклон касательной в точке М к оси х, тангенс этого углу равен, как известно, производной у´: у´ = tg α . Подставляя это выражение в соотношение (1), получим следующее уравнение: у´ = х/(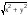 – у). (2)
– у). (2)
Такие уравнения, связывающие независимую переменную х, искомую функцию у и ее производную у´, называются дифференциальными уравнениями. 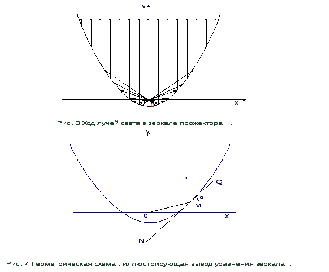
Примеры зависимостей, выраженных через квадратичную функцию.
1.Уравнение координаты тела, движущегося под действием постоянной силы
х = х0 + V0t + 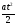
(частные случаи этого движения х0 = 0, V0 = 0).
2. Зависимость кинетической энергии от скорости
W = 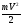 ,
,
электрической мощности от тока N = RI2 и др.
3.В электроизмерительных приборах электромагнитной системы угол поворота стрелки пропорционален квадрату силы тока. Шкалы этих приборов называются квадратичными, они неравномерные.
4.Количество тепла, выделяемого за 1 с при прохождении тока в проводнике с постоянным сопротивлением R Ом и силой тока в 1 ампер выражается квадратичной функцией Q = 0,24 RI² (калорий). Графиком этой функции является правая ветвь параболы с вершиной в начале координат.
5.Груз, сброшенный с самолета на высоте h с начальной скоростью v0 при своем падении описывает правую ветвь параболы, ветви которой направлены вниз, с вершиной (0;h) : y = h -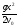 .
.
6.Тело, брошенное под углом  к горизонту с начальной скоростью
к горизонту с начальной скоростью  м/с (без учета сопротивления воздуха), летит по кривой, являющейся параболой: у = x·tg
м/с (без учета сопротивления воздуха), летит по кривой, являющейся параболой: у = x·tg -
-  .
.
Подбор материала к данному уроку можно поручить учащимся, посещающим факультатив и проявляющим интерес к предмету. Материал может быть представлен в форме доклада или в форме компьютерной презентации. Можно использовать также готовый математический этюд (см. сайт www.etudes.ru ).
Задача. Вдоль наклонной доски пустили катиться снизу вверх шарик. На расстоянии 0,5 м от начала пути шарик побывал дважды: через 1 и 4 с после начала движения. Считая движение равнопеременным, определить его начальную скорость и ускорение.
Решение. Здесь  с и
с и  c есть абсциссы точек пересечения параболы, задаваемой формулой
c есть абсциссы точек пересечения параболы, задаваемой формулой  (где
(где  ), с прямой x = l = 0,5. Другими словами, при x = l,
), с прямой x = l = 0,5. Другими словами, при x = l,  и
и  есть корни квадратного уравнения
есть корни квадратного уравнения  , или
, или 
Используя теорему Виета, получаем:
 , значит
, значит  (м/с2) и
(м/с2) и  (м/с2).
(м/с2).
Итог урока









 рис.1
рис.1

 Рис.4
Рис.4 Рис.5
Рис.5




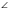 ОМN =
ОМN = 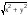

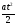
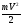 ,
,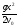 .
.









