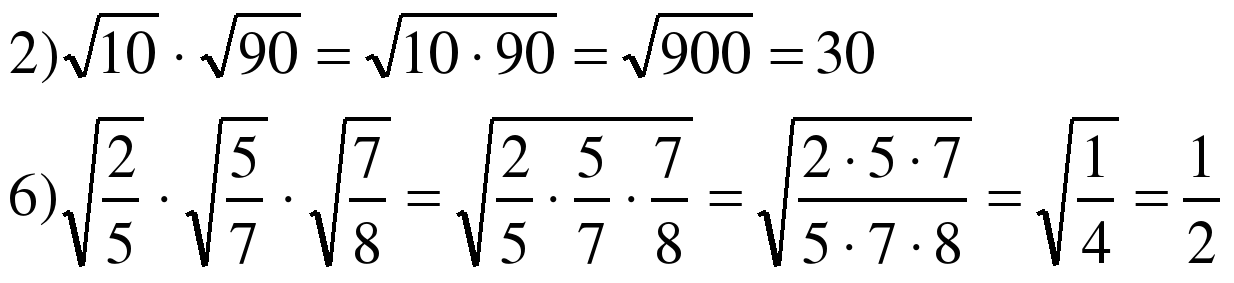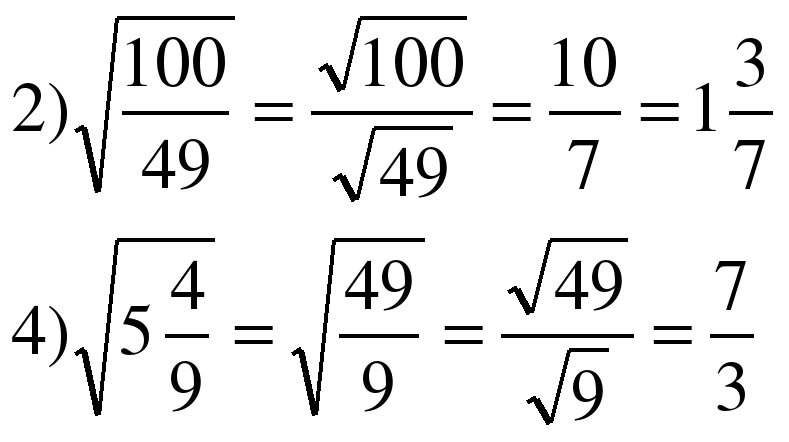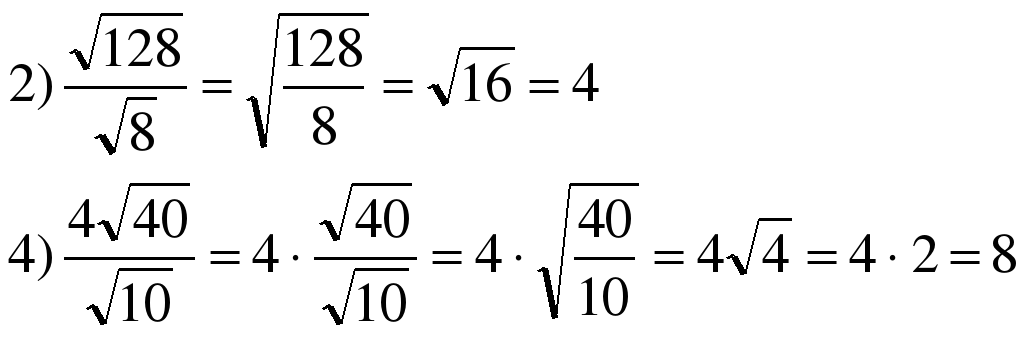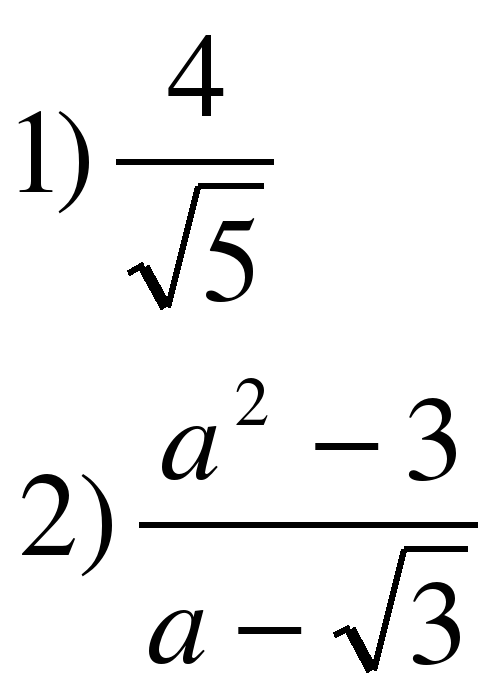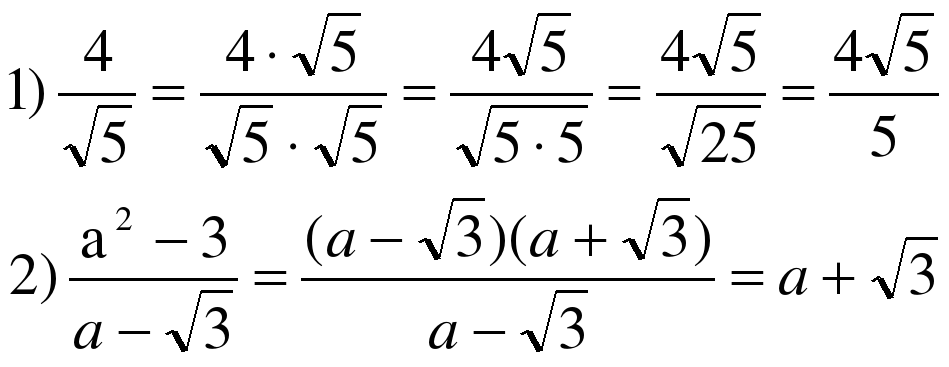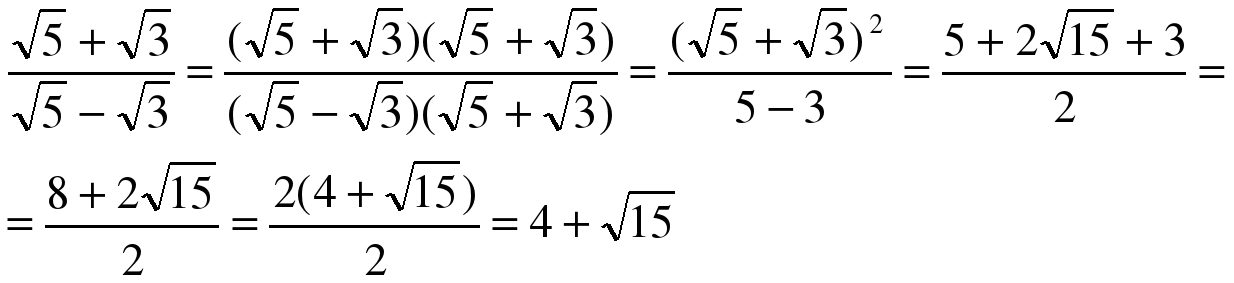Ручина Н., Швецова И.
| Деятельность учителя | Деятельность учащихся |
Мотивационно-ориентировочный этап К началу урока учитель просит двух учеников оформить решение домашнего задания на доске. Один из учеников оформляет №№ 340 (2,4), 343 (2,6), а другой - №№ 362 (2,4), 363 (2,4).
1. Актуализация |
| Начнем урок с проверки домашнего задания. Ученик №1, расскажи, пожалуйста, как ты решал № 340? | 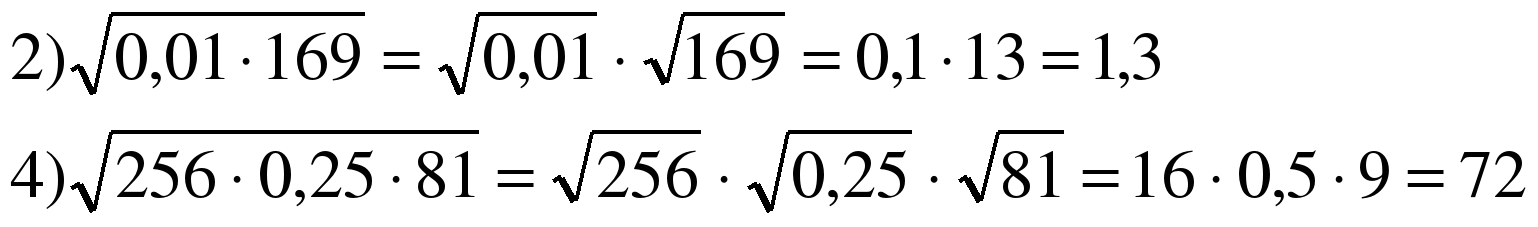 |
| Какой теоремой при решении этих примеров ты пользовался? | Теоремой об извлечении арифметического квадратного корня из произведения. |
| Сформулируй эту теорему. | Корень из произведения неотрицательных множителей равен произведению корней из этих множителей. |
| Хорошо. Запиши, пожалуйста, на доске эту теорему с помощью символов. | Если 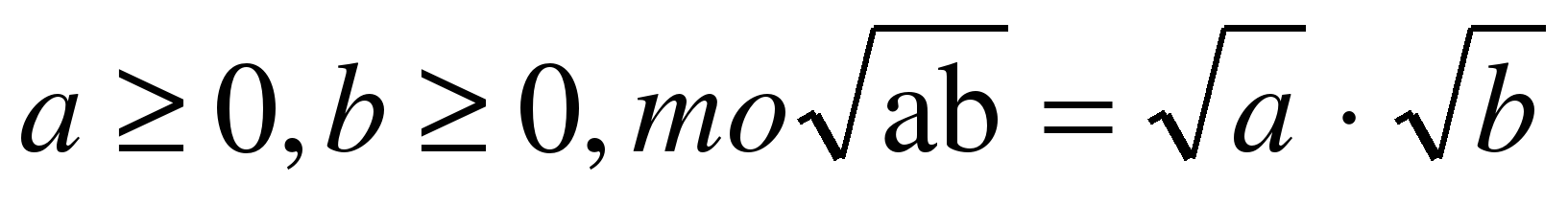 |
| А теперь расскажи, пожалуйста, какой теоремой ты пользовался при решении № 343? | 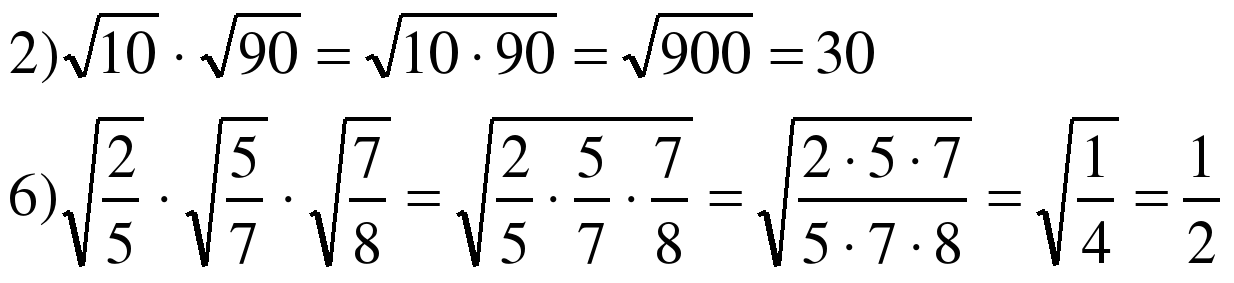 Этой же теоремой, но в обратную сторону. |
| Молодец, можешь садиться. Ученик №2, скажи, пожалуйста, какой теоремой ты пользовался при решении № 362? | 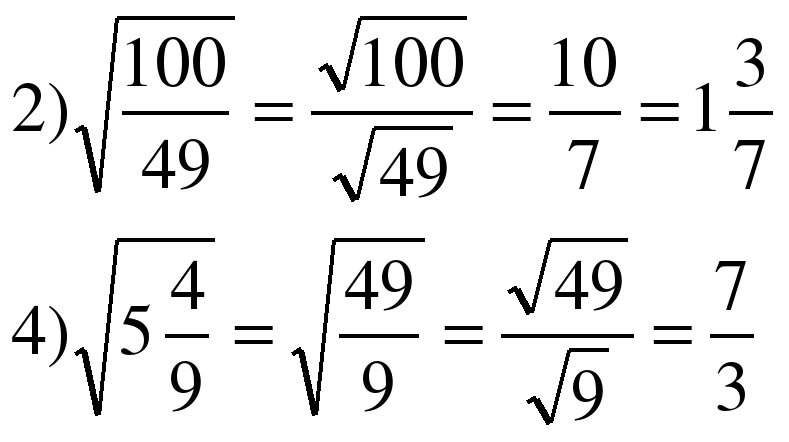 Теоремой об извлечении арифметического квадратного корня из дроби. |
| Сформулируй эту теорему. | Корень из дроби равен корню из числителя, деленному на корень из знаменателя. |
| Хорошо. Запиши ее, пожалуйста, на доске с помощью символов. | Если 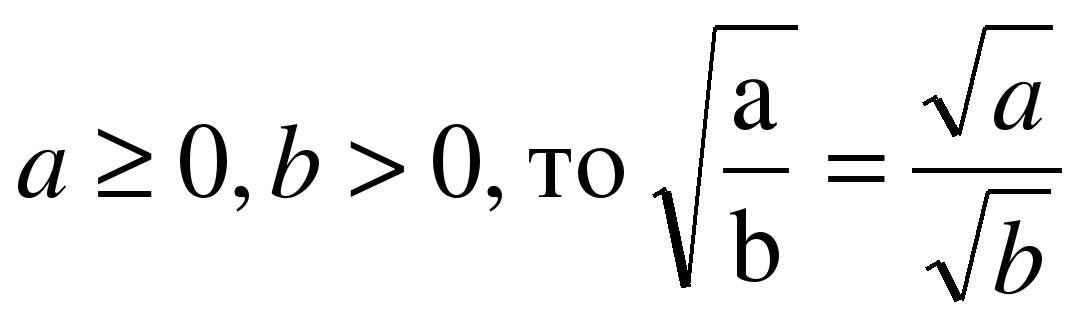 |
| Верно, а как ты решал № 364? Что использовал? | 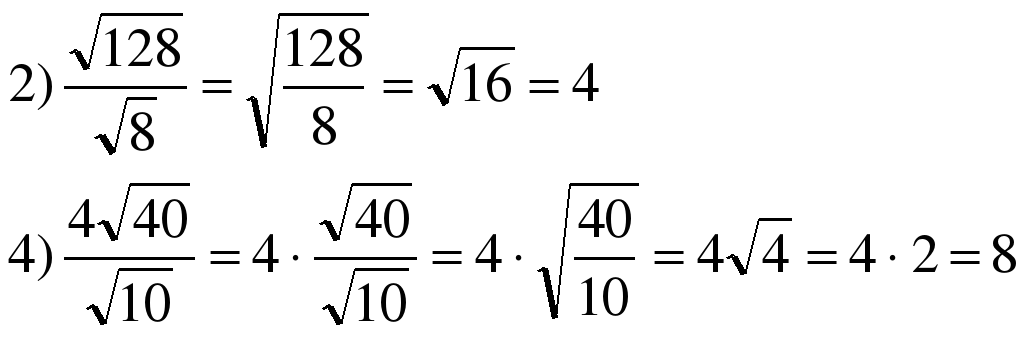 Использовал теорему об извлечении арифметического квадратного корня из дроби, но в обратную сторону. |
| Хорошо, садись, пожалуйста. Давайте теперь вспомним одну из теорем, изученных на прошлых уроках, упростив выражение: 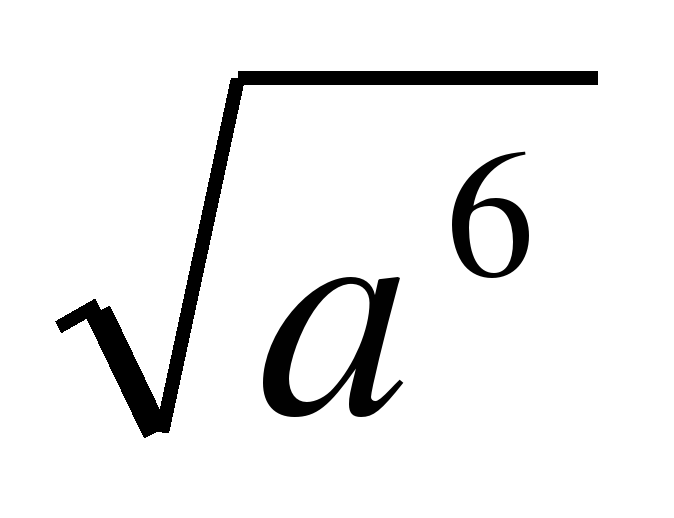 |
(Ученик, вызванный учителем, оформляет решение на доске, а все остальные в своих тетрадях): 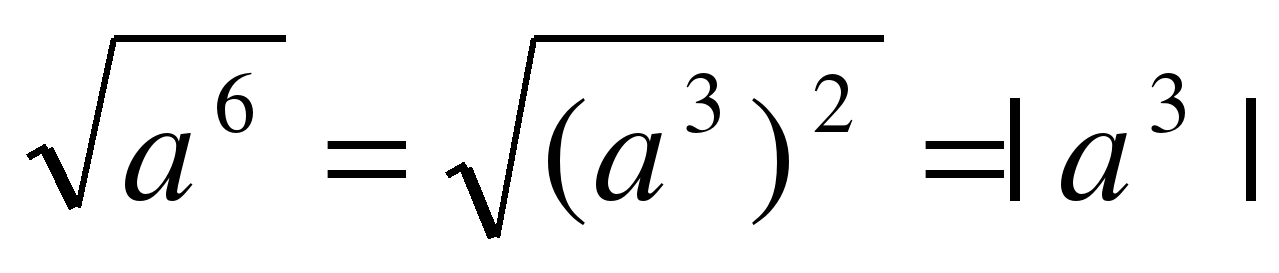 |
| Какой теоремой ты воспользовался при выполнении данного задания? | Воспользовался следующей теоремой: для любого числа а справедливо равенство  |
| Хорошо, но полученный ответ не является оканчательным. Нужно рассмотреть два случая в зависимости от числа а. | Если а ≥ 0, то а3 ≥ 0 и поэтому | а3| = а3 Если а 3 3| = -а3 |
| 2. Мотивация |
| На прошлом уроке было изучено два способа избавления от иррациональности в знаменателе дроби. Вспомним их, решив следующие примеры: 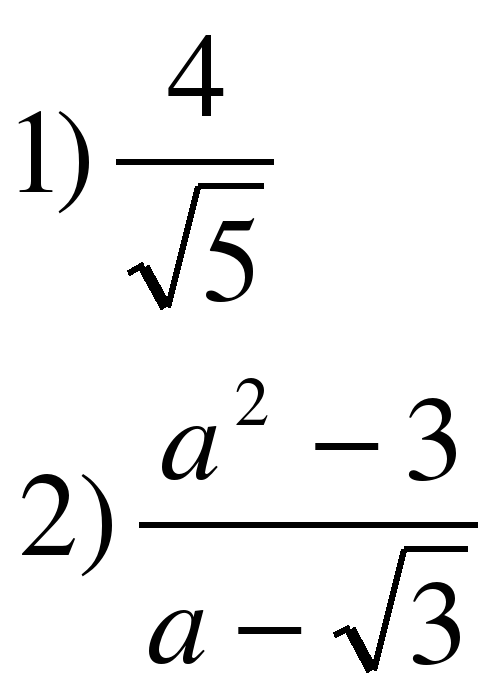 | 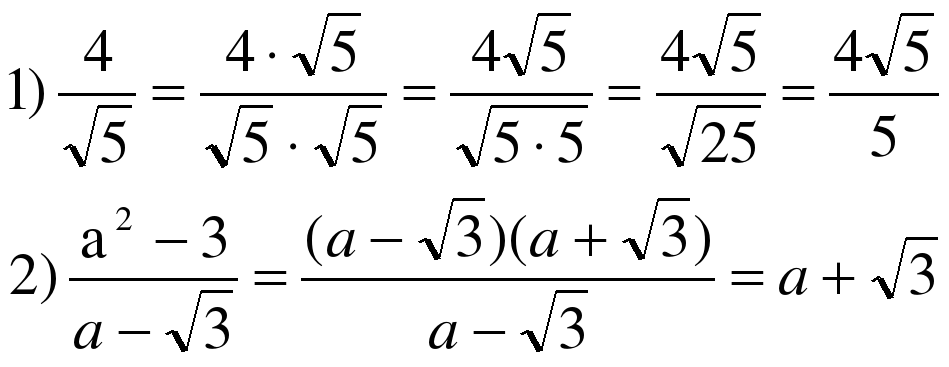 |
| Как вы избавились от иррациональности в знаменателе дроби в первом примере? | Домножили числитель и знаменатель дроби на корень, стоящий в знаменателе. |
| Верно. А каким образом вы избавились от иррациональности в знаменателе дроби во втором примере? | Путем разложения числителя дроби на множители так, чтобы один из сомножителей был равен знаменателю. |
| Хорошо. А теперь попробуйте избавиться от иррациональности в знаменателе следующей дроби:  | (Не могут найти способ решения) |
| Давайте, оставим пока этот пример и попробуем выполнить другие задания: Упростите выражение: 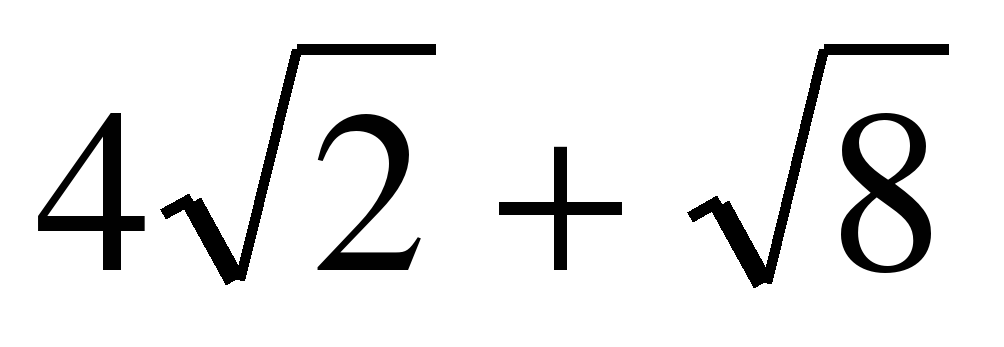 Сравните числа: 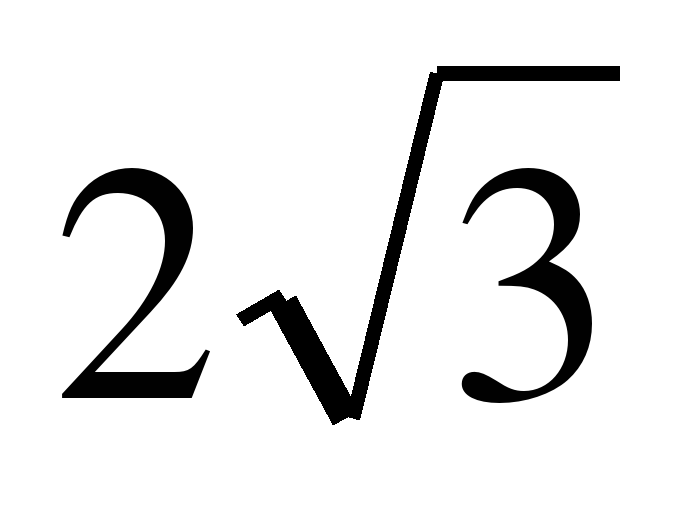 и и 
| (Не могут выполнить задания) |
| 3. Постановка учебной задачи |
| Итак, сегодня мы должны открыть и сформулировать третий способ избавления от иррациональности в знаменателе дроби и научиться применять этот способ; а также выявить основные виды задач на применение изученных теорем и научиться применять эти теоремы для решения более сложных задач. |
|
Содержательный этап |
| Упростите выражение:  | (Один из сильных учеников или сам учитель оформляет решение на доске, а все остальные в своих тетрадях):  |
| Каким образом упрощали это выражение? | Приводили к общему знаменателю, домножая первую дробь на ( ), а вторую на ( ), а вторую на ( ) ) |
| Верно, давайте заметим, что при умножении разности ( ) на сумму ( ) на сумму ( ), мы получили выражение, не содержащие корней. Таким образом, открыли третий способ избавления от иррациональности в знаменателе дроби. Сформу-лируйте его. ), мы получили выражение, не содержащие корней. Таким образом, открыли третий способ избавления от иррациональности в знаменателе дроби. Сформу-лируйте его. | Чтобы избавиться от иррациональности в знаменателе дроби, нужно числитель и знаменатель этой дроби умножить на сумму, если в знаменателе стоит разность или числитель и знаменатель этой дроби умножить на разность, если в знаменетеле стоит сумма. |
| Правильно. Такой способ избавления от иррациональности в знаменателе дроби называется умножением на сопряженное. Теперь, используя это правило, избавьтесь от иррациональности в знаменателе в нерешенном ранее примере:  |
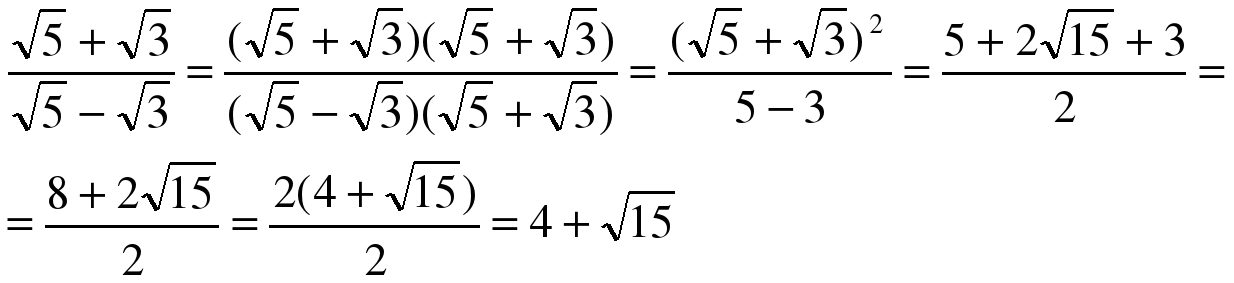 |
| Объясните, как вы избавлялись от иррациональности в знаменателе данной дроби. | Числитель и знаменатель дроби умножили на число ( ), то есть на число, сопряженное знаменателю. ), то есть на число, сопряженное знаменателю. |
| Хорошо. Теперь вы можете решать такие примеры, используя новый способ избавления от иррациональности в знаменателе дроби. А сейчас выполните следующее задание: Вынесите множитель из-под знака корня (буквой обозначено любое число): 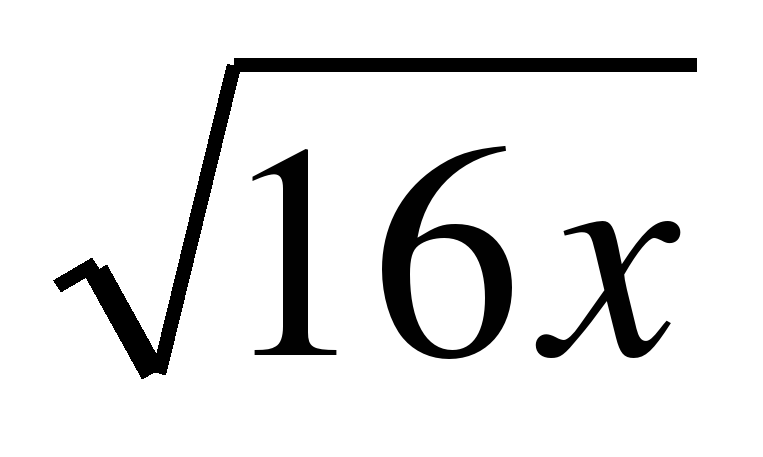 |
|
| Какое действие стоит под знаком корня? | Умножение. |
| Верно, чем тогда можно воспользоваться? | Теоремой об извлечении арифметического квадратного корня из произведения. |
| При каких условиях можно использовать эту теорему? | При а ≥ 0 и b ≥ 0.
|
| В данном случае эти условия выполняются? | Да, выполняются, так как 16 0 и х ≥ 0 (х записано под знаком корня, корень существует). |
| Решите этот пример. | |
| Молодцы. Только что мы научились выносить числовой множитель из-под знака корня. А теперь давайте научимся выносить буквенный множитель из-под знака корня. Выполните следующее задание: Вынесите множитель из-под знака корня (буквой обозначено любое число): |
|
| Какое действие стоит под знаком корня? | Умножение.
|
| Верно, какую теорему тогда будем использовать? | Теорему об извлечении арифметического квадратного корня из произведения. |
| Эта теорема справедлива при определенных условиях. В данном случае они выполняются? | Да, выполняются, так как 3 0 и а ≥ 0 (а записано под знаком корня, корень существует).
|
| Решите этот пример. | |
| Какой еще теоремой вы пользовались при решении? | Пользовались следующей теоремой : для любого числа а справедливо равенство  |
| Правильно. Но пример еще не решен полностью. Запишите, пожалуйста, оканчательный ответ в зависимости от числа а. | Если а ≥ 0, то Если а |
| Верно, таким образом, мы научились выносить буквенный множитель из-под знака корня. А теперь выполните другое задание: Внесите множитель под знак корня: |
|
| Внесите сначала числовой множитель под знак корня. Какую теорему при этом используете? |
Теорему об извлечении арифметического квадратного корня из произведения, но в обратную сторону. |
| Хорошо. Число а какое? Положительное или отрица-тельное? | Число а может быть как и положительное, так и отрицательное.
|
| Заметим, что . А это неверно. Значит, не все так просто. Какие возможны два случая в зависимости от числа а? |
Если а ≥ 0, то Если а |
| Правильно. Итак, мы научились выносить числовой и буквенный множители из-под знака корня, а также вносить числовой и буквенный множители под знак корня. Наконец-то, мы можем выполнить задания, которые не смогли решить ранее: Упростите выражение: 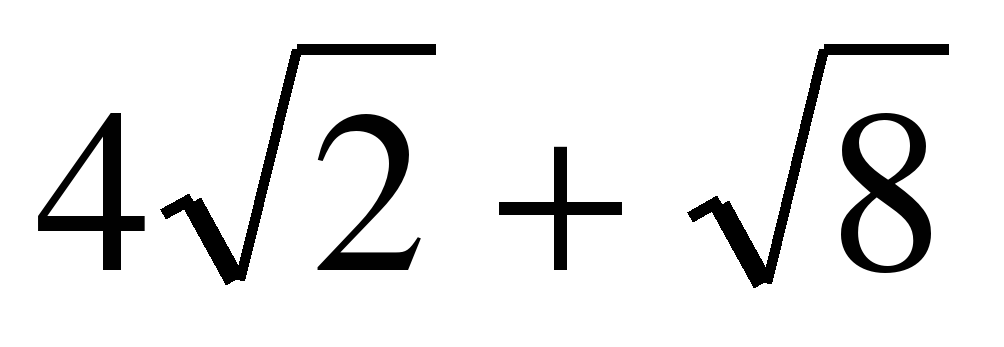 Сравните числа: 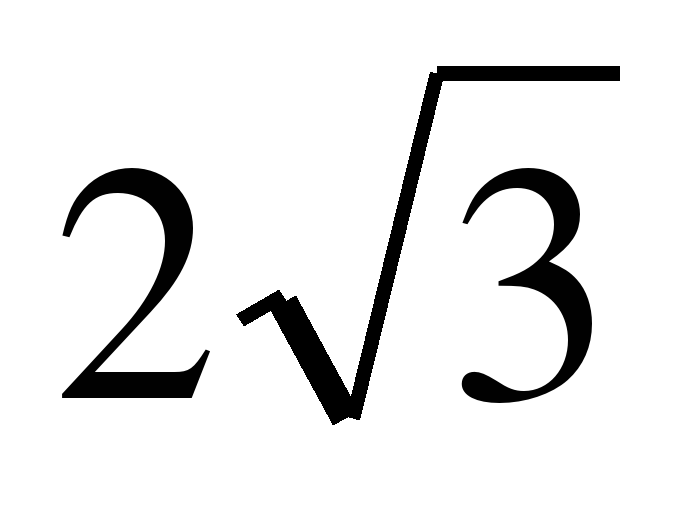 и и  |
|
| Сначала упростим выражение. Какое преобразование нужно выполнить, чтобы упростить данное выражение? |
Нужно вынести числовой множитель из-под знака корня.
|
| Какую теорему при этом используете? | Теорему об извлечении арифметического квадратного корня из произведения. |
| Правильно, давайте оформим решение данного примера. | (Учитель сам оформляет решение на доске):
|
| А теперь сравним два данных числа. Какое преобразование нужно выполнить, чтобы сравнить данные числа? |
Нужно внести числовой множитель под знак корня.
|
| Какую теорему при этом пприменяете? | Теорему об извлечении арифметического квадратного корня из произведения, но в обратную сторону.
|
| Верно, оформим теперь решение. | (Учитель сам оформляет решение на доске): 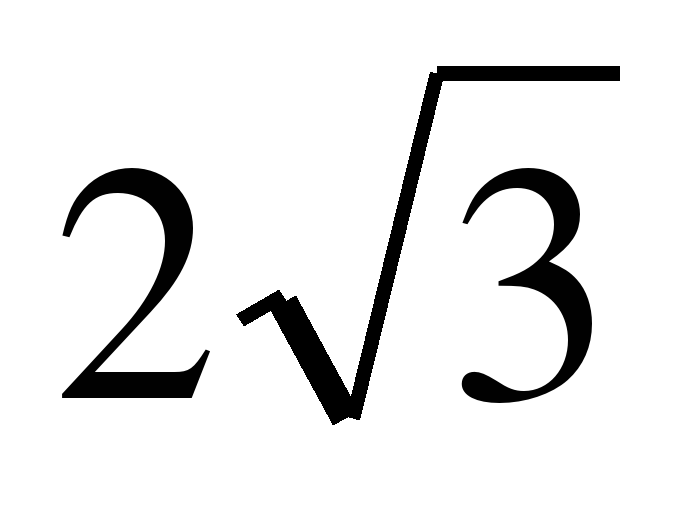 и и  |
| Выполним еще одно задание: № 369 (1) Извлеките корень: |
(Один из сильных учеников или сам учитель оформляет решение на доске, а все остальные в своих тетрадях).
|
| При каком а существует данное выражение? | Данное выражение существует при любом а. |
| Какой теоремой уже можно воспользоваться? | Теоремой об извлечении арифметического квадратного корня из дроби. |
| Какой корень сейчас можно вычислить? | |
| Какое действие стоит под знаком корня в числителе? | Умножение.
|
| Какую теорему тогда можно применить? | Теорему об извлечении арифметического квадратного корня из произведения. |
| Вычисляем теперь полученные корни в числителе, какую при этом теорему используем? | Используем следующую теорему : для любого числа а справедливо равенство  |
| Запиши оканчательный ответ в зависимости от числа а. | Если а ≥0, то Если а |
Рефлексивно-оценочный этап |
| Какова была цель урока? | Выявить основные виды задач на применение изученных теорем, а именно на вынесение множителя из-под знака корня, на внесение множителя под знак корня, открыть и сформулировать третий способ избавления от иррациональности в знаменателе дроби |
| Достигли ли мы ее? | Да |
| Как мы ее достигли? | Мы сформулировали новый способ избавления от иррациональности в знаменателе дроби (умножение на сопряженное): чтобы избавиться от иррациональности в знаменателе дроби, нужно числитель и знаменатель этой дроби умножить на сумму, если в знаменателе стоит разность или числитель и знаменатель этой дроби умножить на разность, если в знаменетеле стоит сумма, то есть числитель и знаменатель этой дроби умножить на число, сопряженное знаменателю. Также выявили основные виды задач на вынесение множителя из-под знака корня, внесение множителя под знак корня и на избавление от иррациональности в знаменателе дроби новым способом. |
| Дается домашнее задание: № 351 (1,4) Внести множитель под знак корня (буквами обозначены положительные числа):
№ 352 (4) Сравнить:
№ 355 (4) Упростить выражение: 4)
№ 366 (3,5,7) Исключить иррациональность из знаменателя:
№ 369 (2,4) Извлечь корень: 2) 4) , где а 0 |
№ 351 (1,4) 1) (Используется теорема об извлечении арифметического квадратного корня из произведения в обратную сторону). 4) (Используется теорема об извлечении арифметического квадратного корня из произведения в обратную сторону).
№352 (4) и (Используется теорема об извлечении арифметического квадратного корня из произведения в обратную сторону). № 355 (4) (Используется теорема об извлечении арифметического квадратного корня из произведения).
№ 366 (3,5,7): (Используется новый способ избавления от иррациональности в знаменателе дроби - умножение на сопряженное).
№ 369 (2,4) 2) (Используется теорема об извлечении арифметического квадратного корня из дроби, теорема об извлечении арифметического квадратного корня из произведения и теорема:  ) ) |