Урок-семинар «РАСЧЕТ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПОВЫШЕННОЙ СЛОЖНОСТИ»*

Урок-семинар
«Расчет электрической цепи
повышенной сложности»^*

Эпиграф:

Знание только тогда знание, когда оно приобретено усилиями своей мысли, а не памятью.

Л. Н. Толстой

Цели: повторить темы «Последовательное и параллельное соединение проводников», «Соединение конденсаторов», закрепить знания, умения при решении задач; ознакомить учащихся с законами Кирхгофа».

Ход урока

I. Вступительное слово преподавателя.

Наш сегодняшний урок посвящен расчету электрических цепей. Потребители и другие элементы цепи могут быть соединены друг с другом различными способами, иногда очень причудливым образом. Но какими бы сложными они ни казались нам на первый взгляд, рассчитать их можно, используя законы последовательного и параллельного соединения резисторов или конденсаторов. Первый этап нашего урока я назвала «Нам эти законы запомнить несложно!», и проведем мы на этом этапе урока эстафету. Каждый ряд – это команда, участвующая в эстафете. Команда получает одинаковые задания. Учитель передает листы с заданиями учащимся, сидящим справа за первыми партами. Те записывают ответ на первый вопрос (на специально оставленном листе) и передают лист на вторую парту и т. д. Когда ученик, сидящий справа за последней партой, ответив на вопрос, передает задание товарищу слева. Тот после ответа – товарищу, сидящему за предыдущей партой, и т. д. Полностью заполненный лист передают преподавателю. (Возле своего вопроса ученик пишет фамилию.)

Задания:

1. При последовательном соединении конденсаторов (рис. 1):

С =

Рис. 1

2. При последовательном соединении n одинаковых конденсаторов:
если С₁ = С₂ = ....... = С_n

С =

3. При параллельном соединении конденсаторов (рис. 2):

С =

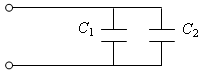
Рис. 2

4. При параллельном соединении n одинаковых конденсаторов:
если С₁ = С₂ = ....... = С_n

С =

5. При последовательном соединении проводников (рис. 3):

R =

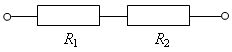
Рис. 3

6. При последовательном соединении n одинаковых проводников:
если R₁ = R₂ = ....... R_n, то R =

7. При параллельном соединении проводников (рис. 4):

R =

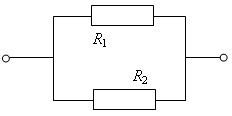
Рис. 4

8. При параллельном соединении n одинаковых проводников:
если R₁ = R₂ = ....... = R_n, то R =

Устно проговариваются правильные ответы.

II. Задачи среднего уровня сложности.

Предлагаются смешанные соединения либо резисторов, либо конденсаторов. К доске приглашаются по одному представителю от каждого варианта (всего 6 человек). Трое решают задания на соединения резисторов, трое – конденсаторов.

Задания:

1. Найдите сопротивление между точкамиА и В электрической схемы, представленной на рис. 5.

Рис. 5

Ответ:R_об = R.

2. Определите сопротивление участка АВ, если R = 1 Ом (рис. 6).

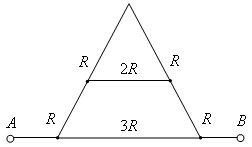
Рис. 6

Ответ: 1,5 Ом.

3. Вычислите сопротивление участка цепи, изображенного на рис. 7, если R = 20 Ом.

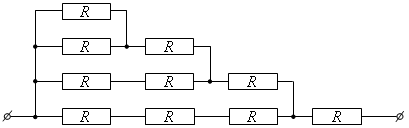
Рис. 7

Ответ: 4,3 Ом.

4. Определите электроемкость батареи конденсаторов, если
С₁ = С₂ = 2 мкФ, С₃ = С₄ = С₅ = 6 мкФ (рис. 8).

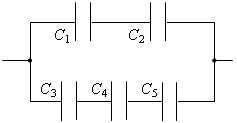
Рис. 8

Ответ: 3 мкФ.

5. Определите электроемкость батареи конденсаторов. Все конденсаторы имеют емкостьС (рис. 9).

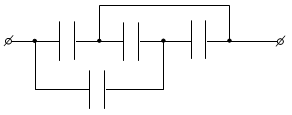
Рис. 9

Ответ: .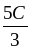

6. Определите электроемкость батареи конденсаторов. Все конденсаторы имеют емкостьС (рис. 10).

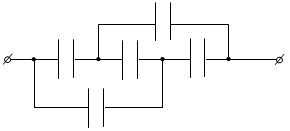
Рис. 10

Ответ:С.

III. «Задачи по частям».

– Для решения предлагаются задача и «ключ» ее решения, состоящий из нескольких пунктов, то есть решать ее мы будем, выходя по очереди, каждый ученик использует свой пункт «ключа».

Задача для учащихся с первого ряда.

К доске приглашается учащийся, не участвовавший во втором этапе урока.

В схеме, изображенной на рисунке 11, емкость батареи конденсаторов не изменяется при замыкании ключа K. Определите электроемкость конденсатора С_х.

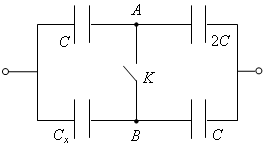
Рис. 11

«Ключ» к решению.

1) Определите электроемкость батареи конденсаторов при разомкнутом ключе: .

Приглашается к доске второй учащийся с первого ряда. Для него:

2) определить электроемкость батареи конденсаторов при замкнутом ключе: .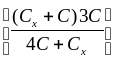

Задание для третьего ученика с первого ряда:

3) приравнять величины, полученные в п. 1 и 2, так как емкость батареи конденсаторов не изменяется при замыкании ключа, и найти С_х:

9 (С_х + С)² = (5С_х + 2С) (4С + С_х)  9С² + 18С_хС + 9С² = 20СС_х +
+ 8С² + 5С_х² + 2СС_х;

4С_х² – 4СС_х + С² = 0 Д = 16С² – 16С² = 0 С_х = .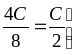

Задача для учащихся со второго ряда.

В цепи, схема которой изображена на рисунке 12, сопротивления всех резисторов одинаковы и равны R = 2 Ом. Найти общее сопротивление цепи R₀.

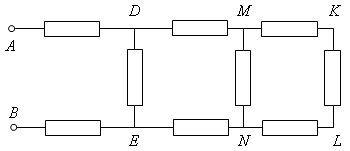
Рис. 12

«Ключ» к решению.

1) Найти общее сопротивление ветвей MN и MKLN – R_MN (они соединены параллельно:

R_MN = R).

2) Найти сопротивление участка DMNE – R_DMNE (два сопротивления на участках DM и NE соединены последовательно с сопротивлением R_MN:

R_DMNE = R + 2R = R).

3) Найти общее сопротивление ветвей DE и DMNE (они соединены параллельно, поэтому R_DE = R).

4) Найти общее сопротивление ветвей AD, DE и BE, оно же общее сопротивление цепи R_об (названные ветви соединены последовательно):

R_об = 2R + R = = 5,5 Ом.

Задача для учащихся с третьего ряда.

Между клеммамиА и В включены конденсаторы, как показано на рисунке 13. Найти емкость системыС, если:

С₁ = 2 мкФ = 2 · 10^–6 Ф;

С₂ = 1 мкФ = 10^–6 Ф.

Рис. 13

«Ключ» к решению.

1) Найти емкость участка цепи между точками D и F – C_DF (он состоит из двух параллельных ветвей, в одну из которых включен конденсатор С₂, а в другую – последовательно три конденсатора емкостями C₁):

C_DF = С₂ + С_об, где С_об = C_DF = С₂ + .

2) Найти общую емкость участков AD и BF – C_{AD + ВF} (участки соединены последовательно и емкости участков одинаковые):

C_{AD + ВF} = .

3) Найти общую емкость всей батареи конденсаторовС (так как участки AD, DF и FB соединены последовательно):

4) Произвести расчет общей емкости батареи конденсаторов:

IV. Знакомство с правилами Кирхгофа, часто применяемыми для расчета сложных электрических цепей.

Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:

Токи, подходящие к узлу, считаются положительными, а токи, исходящие из узла, – отрицательными.

Второе правило Кирхгофа: в любом замкнутом контуре алгебраическая сумма произведений сил токов на сопротивление соответствующих участков равна алгебраической сумме ЭДС в контуре. Токи, совпадающие по направлению с выбранным направлением обхода контура, считаются положительными, а несовпадающие – отрицательными. ЭДС берется со знаком «+», если переход внутри источника от отрицательного полюса к положительному, и со знаком «–» в противном случае.

Применим эти правила для решения следующей задачи.

Задача 1. Три источника тока с электродвижущими силами ℰ₁ =
= 2,5 В; ℰ₂ = 2 В; ℰ₃ = 15 В и резисторами R₁ = 2 Ом; R₂ = 3 Ом; R₃ = 8 Ом соединены, как показано на рисунке 14. Определите токи через эти резисторы. Внутренним сопротивлением источников пренебречь.

Рис. 14

По первому правилу Кирхгофа: для узлаА:

– J₁ – J₂ + J₃ = 0

По второму правилу Кирхгофа для контураАℰ₂Вℰ₁А:

– ℰ₁ + ℰ₂ = J₁R₁ – J₂R₂;

для контураАℰ₃Вℰ₂А:

–ℰ₂ + ℰ₃ = J₂R₂ + J₃R₃;

для контура AE₃BE₁A:

ℰ₁ – ℰ₃ = –J₁R₁ – J₃R₃.

Подставим в эти формулы численные значения из условия задачи:

J₁ + J₂ = J₃

– 0,5 = – 3J₂ + 2J₁

13 = 3J₂ + 8J₃

12,5= –2J₁ –8J₃

13 = 3J₂ + 8(J₁ + J₂) = 3J₂ + 8J₁ + 8J₂ = 11J₂ + 8J₁.

Далее решаем систему: и находим J₂ = = 0,65A,
J₁ = 0,73 A, J₃ = 1,38 A.

Проверяем решение по первому правилу Кирхгофа:

0,65 + 0,73 = 1,38 (А).

Задача 2. Два элемента с ЭДС ℰ₁ = 1,25 В и ℰ₂ = 1,5 В, имеющие одинаковые внутренние сопротивления r₁ = r₂ = 0,4 Ом, соединены параллельно и замкнуты резистором, сопротивление которого R = 10 Ом. Найти силы токов в резисторе и в каждом элементе (рис. 15).

Рис. 15

Решение. Обозначим направления токов и выберем направление обхода контуров так, как показано на рисунке.

По первому правилу Кирхгофа: для узлаА: J – J₁ – J₂ = 0.

По второму правилу Кирхгофа: для контура Aℰ₁BRA: J₁r₁ + JR = ℰ₁ для контура Aℰ₁Bℰ₂A: J₁r₁ – J₂r₂ = ℰ₁ – ℰ₂.

Подставив числовые значения ЭДС и сопротивления, получим систему уравнений:

Решив эту систему, получим: J ≈ 0,135 A, J₁ ≈ – 0,245 A, J₂ ≈ 0,38 А.

Значение силы тока J₁ получилось отрицательным, это указывает на то, что действительное направление данного тока противоположно обозначенному.

Задачи для самостоятельного решения.

1. Две батареи (ℰ₁ = 10 В, r₁ = 1 Ом; ℰ₂ = 8 В, r₂ = 2 Ом) и резистор
R = 6 Ом соединены, как показано на рисунке 16. Определить силу тока в батареях и резисторе.

Рис. 16

Ответ:J₁ = 6,4 A; J₂ = 5,8 A; J₃ = 0,6 А.

2. Два источника тока (ℰ₁ = 8 В, r₁ = 2 Ом, ℰ₂ = 6 В, r₂ = 1,5 Ом) и резистор R = 10 Ом соединены, как показано на рисунке 17. Определить силу тока, текущего через реостат.

Рис. 17

Ответ:J = 0,63 A.

Задачи решаются по вариантам на отдельных листочках, сдаются учителю на проверку.

V. Подведение итогов урока.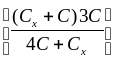
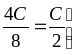