Урок: Системы нелинейных неравенств с одной переменной.

Оценка: определяют результаты своей работы на уроке

Синтез: формулируют алгоритм решения системы нелинейных неравенств с одной переменной, развивают навыки решения систем неравенств

Анализ: сравнивают методы решения системы нелинейных неравенств с одной переменной, изучают алгоритмы решения

Применение: демонстрируют применение алгоритма решения системы нелинейных неравенств с одной переменной

Понимание: обсуждают способы решения системы нелинейных неравенств с одной переменной, их алгоритм решения

Знание: рассказывают алгоритм решения системы нелинейных неравенств с одной переменной

Учебно-воспитательные задачи:

Образовательная:

обеспечить усвоение новых знаний по данной теме, закрепить навыки решения системы нелинейных неравенств с одной переменной

Развивающая: развитие способности выражать мысли, познавательных способностей, формирование алгоритмического мышления, расширение кругозора

Воспитательная: способствовать выявлению, раскрытию способностей учащихся, возбуждать интерес к предмету, побуждать учащихся к применению полученных знаний

Результаты обучения:

Учащиеся знают: алгоритм решения системы нелинейных неравенств с одной переменной

Учащиеся умеют: решать системы нелинейных неравенств с одной переменной

Этапы урока

Содержание этапа

Оргмомент.

Задачи: обеспечить нормальную внешнюю обстановку на уроке, психологически подготовить детей к общению

Приветствие

Проверка подготовленности к уроку

Организация внимания школьников

Ознакомление с планом проведения урока

Проверка домашнего задания.

Задачи: установить правильность, полноту и осознанность выполнения всеми учащимися домашнего задания, выявить пробелы в знаниях, устранить в ходе проверки обнаруженные пробелы

Выявление степени усвоения заданного учебного материала

Фронтальный опрос.

Ликвидация обнаруженных недостатков.

Вызов.

Задачи: обеспечить включение школьников в совместную деятельность по определению целей учебного занятия.

Сообщение темы урока

Формулирование цели совместно с учениками

Показ значимости изучаемого материала

Постановка проблемы

Актуализация знаний и умений

Задачи: психологическая подготовка ученика: сосредоточение внимания, осознание значимости предстоящей деятельности, возбуждение интереса к уроку; учащиеся воспроизводят известные им знания, осознают их, обобщают факты, связывают старые знания с новыми условиями, с новыми данными и т.д. 

Толстые и тонкие вопросы

Что такое неравенство?

Что значит решить неравенство?

Какие способы решения квадратных неравенств вы знаете?

Объясните метод параболы

Объясните метод интервалов

Озвучивают тему урока.

Отвечают на вопросы учителя. Осознают проблему.

Формулируют цели: закрепить навыки решения системы нелинейных неравенств с одной переменной

Осмысление

Изучение нового материала.

Задачи: обеспечить восприятие, осмысление и первичное запоминание изучаемого материала, осознание своих способов проработки учебной информации

Деление на группы:1)- Ребята, а сейчас приступаем к изучению новой темы. Итак, каждая группа получит свое задание. Ваша задача в течение 8 минут раскрыть свою тему в виде схемы, кластера. Для этого я вам предлагаю использовать бумагу и фломастеры. Таймспикеры должны обязательно следить за временем. После того, как все команды будут готовы, мы выслушаем выступление каждой группы (2мин).

Критерии оценивания выступления:

а)Доступность изложения; б) Оформление; в)Регламент

Задание группам:

1. Понятие определения «Системы нелинейных неравенств с одной переменной».

2. Алгоритм решения неравенства второй степени с одной переменной.

3. Решение неравенства второй степени по алгоритму.

4. Решение системы нелинейных неравенств с одной переменной.

Раздатка для групп:

1 группа - «Понятие определения «Системы нелинейных неравенств с одной переменной»

Задание:

1) дать определение системы нелинейных неравенств с одной переменной,

2) указать отличия от других систем неравенств,

3) что значить решить систему нелинейных неравенств

4) что является решением системы нелинейных неравенств с одной переменной.

5) данные системы систематизировать по типу линейные и нелинейные.

2 группа - Алгоритм решения неравенства второй степени с одной переменной.

Задание: учащимся выдается алгоритм в неправильном расположении, их цель сформировать правильный алгоритм решения.

Алгоритм решения квадратного неравенства ax ²+ bx + c0 , (ax ² + bx + c

1. Рассмотрим функцию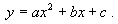 

2. Находим точки пересечения параболы 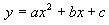с осью OX, для чего решаем уравнение 

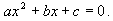3. Определяем направление ветвей параболы.

4. Схематично изображаем параболу, не обозначая координат ее вершины.

5. С помощью графика находим промежутки, в которых функция 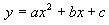принимает положительные (отрицательные) значения.

6. Записываем ответ.

(готовый алгоритм учащиеся крепят на плакат и при выступлении показывают всем ребятам)

3 группа - Решение неравенства второй степени.

Задание: из полученного материала с решением нелинейного неравенства с одной переменной, нужно сформировать верное решение согласно алгоритму решения нелинейного неравенства с одной переменной.

Решить неравенство - 2х² + Зх + 9 Решение.

у=- 2х² + Зх + 9

2) Найдем корни квадратного трехчлена - 2х² + Зх + 9 =0: х₁ = 3; х₂ = - 1,5. (точки пересечения с с осью оХ)

3) Ветви параболы направлены вниз, поскольку старший коэффициент — отрицательное число - 2.

4) Схематично изображаем параболу, не обозначая координат ее вершины.

.5) Используя рис., делаем вывод: у 6) Ответ: х 3.

4 группа- Решение системы нелинейных неравенств с одной переменной.

Рассмотреть решение в учебнике решение примеров 1 и 2 по данному решению составить алгоритм решения системы нелинейных неравенств с одной переменной.

Выступление групп

После выступления групп.

Ну а теперь я прошу все проголосовать за работы друг друга, используя стикеры, которые у вас есть на партах. Голосуем за ту работу, в которой на ваш взгляд лучше всего раскрыт вопрос команды. За свою работу категорически нельзя голосовать.

ПОДВЕДЕНИЕ итогов голосования.

Закрепления новых знаний и умений.

Задачи: обеспечить повышение уровня осмысления учащимися изученного материала, глубины его усвоения

Системы неравенств:

2)  3)  4) 5) 

Проверка новых знаний

Задачи: установить правильность и осознанность учащимися изученного материала, выявить пробелы первичного осмысления

Работа с учебником. № 133(2,4),134(1)

Коррекция знаний.

Задачи: скорректировать выявленные проблемы

Организация деятельности учащихся по коррекции выявленных недостатков

Индивидуальное задание.

Повторное разъяснение учителя.

1. Подведение итогов. Рефлексия.

Задачи: инициировать рефлексию учащихся по поводу своего эмоционального состояния, дать оценку работе отдельных учащихся и всего класса

Мобилизация учащихся на рефлексию.

1. Что у вас удалось при выполнении задания?

2. Была ли работа группы слаженной?

3. Что не получилось, на ваш взгляд?

4. Назовите сильные и слабые стороны команды?

5. Прокомментируйте лист оценивания вашей группы.

Выставление оценок.