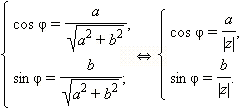МИНИСТЕРСТВО ПРОСВЕЩЕНИЯ ПМР
ГОУ «ДНЕСТРОВСКИЙ ТЕХНИКУМ ЭНЕРГЕТИКИ
И КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ»
УТВЕРЖДАЮ
Зам. директора по учебной работе
__________________М.В. Питель
«_____»__________________2019 г
В ПОМОЩЬ СТУДЕНТУ-ЗАОЧНИКУ
по дисциплине: «МАТЕМАТИКА»
РАЗДЕЛ № 6
«Комплексные числа»
Разработал преподаватель математики
ГОУ СПО «ДТЭ и КТ»
Демьянова Светлана Васильевна
РАССМОТРЕНО СОГЛАСОВАНО
на заседании ЦМК методист
_____________________ дисциплин ________ Левицкая И.Н. Протокол №__ от «__»_____201__г. «__» _________201__г.
Председатель __________________
______________________________
г. Днестровск, 2019 г.
СОДЕРЖАНИЕ
Введение……………………………………………………………………………………………….....3
Глава I. Комплексные числа………………………………………………………………………..…4
Понятие комплексного числа.……………………………………………………………………....4
Операции над комплексными числами.…………………………………………………………....7
Тригонометрическая форма записи комплексных чисел..………………………………………..10
Глава II. Практика……………………………………………………………………………………..13 2.1. Найти число, сопряженное к комплексному числу.……………………………………………...13 2.2. Найти модуль и аргумент комплексного числа………………………………………………..…13 Глава III. Презентация……………………………………………………………………………...…14 Заключение…………………………………………………………………………………………...…15 Список использованной литературы………………………………………………………………..16
ВВЕДЕНИЕ
В зачетной работе написано одного из основных разделов математического анализа теории комплексных чисел. Рассмотрены все типы комплексных чисел, изучаемых в курсе высшей математики. Для каждого типа приведены основные теоретические сведения, приведены примеры решения комплексных чисел и сделана презентация.
Глава I. Комплексные числа.
Понятие комплексного числа.
Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом:
Два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда
Суммой двух комплексных чисел a + ib и c + id называется комплексное число
Произведением двух комплексных чисел a + ib и c + id называется комплексное число
Комплексные числа часто обозначают одной буквой, например, z = a + ib. Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается a = Re z. Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z. Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел.
Заметим, что арифметические операции над комплексными числами вида z = a + i · 0 осуществляются точно так же, как и над действительными числами. Действительно,
Следовательно, комплексные числа вида a + i · 0 естественно отождествляются с действительными числами. Из-за этого комплексные числа такого вида и называют просто действительными. Итак, множество действительных чисел содержится в множестве комплексных чисел. Множество комплексных чисел обозначается С. Мы установили, что 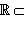
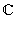 , а именно
, а именно 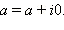
В отличие от действительных чисел, числа вида 0 + ib называются чисто мнимыми. Часто просто пишут bi, например, 0 + i3 = 3i. Чисто мнимое число i1 = 1i = i обладает удивительным свойством:
Таким образом, 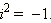
С учётом этого замечательного соотношения легко получаются формулы сложения и умножения для комплексных чисел. Нет нужды запоминать сложную формулу для произведения комплексных чисел – если на комплексные числа смотреть как на многочлены с учётом равенства i2=-1 то и перемножать эти числа можно как многочлены. В самом деле,
то есть как раз получается нужная формула.
Геометрическая интерпретация действительных чисел является действительная прямая. Кроме того, как было установлено выше, на действительной прямой «нет места для новых точек», то есть любой точке на действительной оси отвечает действительное число. Следовательно, комплексные числа на этой прямой расположить уже нельзя, однако можно попытаться рассмотреть наряду с действительной осью, на которой мы будем откладывать действительную часть комплексного числа, ещё одну ось, ей перпендикулярную; будем называть её мнимой осью. Тогда любому комплексному числу z = x + iy можно поставить в соответствие точку координатной плоскости. На оси абсцисс будем откладывать действительную часть комплексного числа, а на оси ординат – мнимую часть. Таким образом мы построим взаимнооднозначное соответствие между всеми комплексными числами и всеми точками плоскости. Если такое соответствие построено, то координатная плоскость называется комплексной плоскостью.
Очень важной является интерпретация комплексного числа z = a + ib как вектора 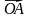 с координатами (a; b) на комплексной плоскости с началом в точке O (0; 0) и концом в точке A с координатами (a; b). Ясно, что это соответствие является взаимнооднозначным. В самом деле, как было только что отмечено, любому комплексному числу z = a + ib соответствует вектор
с координатами (a; b) на комплексной плоскости с началом в точке O (0; 0) и концом в точке A с координатами (a; b). Ясно, что это соответствие является взаимнооднозначным. В самом деле, как было только что отмечено, любому комплексному числу z = a + ib соответствует вектор 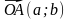 и наоборот, каждому вектору
и наоборот, каждому вектору 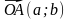 соответствует, и притом единственное, число z = a + ib (Рисунок 1).
соответствует, и притом единственное, число z = a + ib (Рисунок 1).
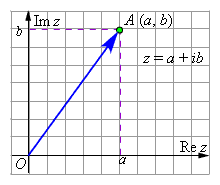
Рис. 1
Рассмотренные интерпретации комплексного числа позволяют называть комплексное число вектором или точкой на комплексной плоскости (Рисунок 2).
| Рис. 2.Комплексные числа на плоскости |
Модулем комплексного числа называется длина вектора, соответствующего этому числу:
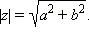
Модуль комплексного числа z обычно обозначается 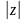 или r. Указанная в определении формула легко выводится при помощи теоремы Пифагора (Рисунок 3).
или r. Указанная в определении формула легко выводится при помощи теоремы Пифагора (Рисунок 3).
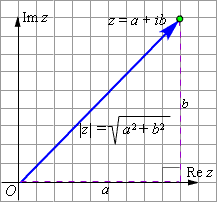
Рис.3
Если 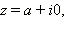 то
то 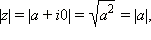 то есть для действительного числа модуль совпадает с абсолютной величиной. Ясно, что
то есть для действительного числа модуль совпадает с абсолютной величиной. Ясно, что 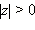 для всех
для всех 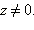 При этом
При этом 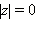 тогда и только тогда, когда
тогда и только тогда, когда 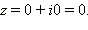
Аргументом комплексного числа z = a + ib (z ≠ 0) называется величина угла между положительным направлением действительной оси и вектором 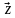 величина угла считается положительной, если угол отсчитывается против часовой стрелки, и отрицательным в противном случае.
величина угла считается положительной, если угол отсчитывается против часовой стрелки, и отрицательным в противном случае.
Угол φ, аргумент комплексного числа, обозначается φ = arg z. Для числа z = 0 аргумент не определён.
Отметим следующий важный факт: заданием своего модуля и аргумента комплексное число фиксируется однозначно. Обратное, вообще говоря, неверно: если задано комплексное число z ≠ 0, то его модуль определяется однозначно, а аргумент – нет. Действительно, если φ = arg z – аргумент этого комплексного числа, то все числа вида φ + 2πn также будут аргументами этого комплексного числа. Например, аргументами комплексного числа z = 1 + i являются углы 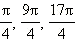 и т. д. Поэтому в качестве аргумента комплексного числа обычно выбирают значение –π ≤ arg z ≤ π. Заданием только лишь своего модуля определяется только комплексное число z = 0. Из определения тригонометрических функций следует, что φ = arg z тогда и только тогда, когда для этого φ выполняется система
и т. д. Поэтому в качестве аргумента комплексного числа обычно выбирают значение –π ≤ arg z ≤ π. Заданием только лишь своего модуля определяется только комплексное число z = 0. Из определения тригонометрических функций следует, что φ = arg z тогда и только тогда, когда для этого φ выполняется система
Операции над комплексными числами.
Арифметические операции над комплексными числами были определены в предыдущем пункте. Эти операции обладают следующими свойствами:
Коммутативность сложения: z1 +z2=z2+z1
для любых z1 ,z2 .
.
| (z1 + z2) + z3 = z1 + (z2 + z3) |
Ассоциативность сложения:
для любых z1 ,z2 .
.
Существует такое число z = 0, которое обладает свойством z+0=z
для любого z  .
.
Для любых двух чисел z1 и z2 существует такое число z, что z1 + z = z2. Такое число z называется разностью двух комплексных чисел и обозначается z = z2 – z1.
Коммутативность умножения: z1z2= z2z1
для любых z1z2 
Ассоциативность умножения: (z1z2) z3= z1(z2 z3)
для любых z1,z2,z3  .
.
Дистрибутивность сложения относительно умножения: z1(z2+z3)= z1z2 +z1 z3
для любых z1,z2,z3  .
.
Для любого комплексного числа z: z∙1=z.
Для любых двух чисел z1 и z2 существует такое число z, что z1∙z=z2 Такое число z называется частным двух комплексных чисел и обозначается  Деление на 0 невозможно.
Деление на 0 невозможно.
Все указанные свойства доказываются с помощью определения операций сложения и умножения.
Рис. 4 Сложение и вычитание комплексных чисел
Рис. 5 Умножение и деление комплексных чисел
Если число z = a + bi, то число  называется комплексно сопряжённым с числом z.
называется комплексно сопряжённым с числом z.
Рис. 6 Комплексное сопряженные числа
Комплексно сопряжённое число обозначается 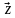 . Для этого числа справедливы соотношения:
. Для этого числа справедливы соотношения:
Заметим, что последнее соотношение сводит операцию деления комплексных чисел к умножению z1 на z2 последующему делению на действительное число  .
.
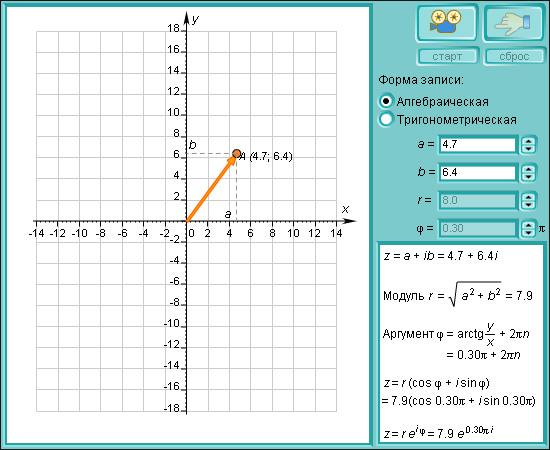
Тригонометрическая форма записи комплексных чисел.
Та запись комплексного числа, которую мы использовали до сих пор, называется алгебраической формой записи комплексного числа. Часто бывает удобна немного другая форма записи комплексного числа. Пусть и φ = arg z. Тогда по определению аргумента имеем:
Отсюда получается
Такая форма называется тригонометрической формой записи комплексного числа. Как видно, для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов. Арифметические действия над комплексными числами, записанными в тригонометрической форме, производятся следующим образом. Пусть
z1 =
r1(cos φ
1 +
i sin φ
1) и
z2 =
r2(cos φ
2 +
i sin φ
2). Имеем:
Видно, что в тригонометрической форме операции умножения и деления производятся особенно просто: для того, чтобы перемножить (разделить) два комплексных числа, нужно перемножить (разделить) их модули и сложить (вычесть) их аргументы.
Отсюда следует, что для того чтобы перемножить n комплексных чисел, нужно перемножить их модули и сложить аргументы: если φ1, φ2, ..., φn – аргументы чисел z1, z2, ..., zn, то
В частности, если все эти числа равны между собой, то получим формулу, позволяющую возводить комплексное число в любую натуральную степень.
Первая формула Муавра:
Число z называется корнем степени n,n из комплексного числа w, если
из комплексного числа w, если  Корень степени n,n
Корень степени n,n обозначается
обозначается  Пусть теперь число w фиксировано. Найдём z из уравнения
Пусть теперь число w фиксировано. Найдём z из уравнения  .
.
Если w = 0, то у уравнения  существует единственное решение z = 0.
существует единственное решение z = 0.
| Если w ≠ 0, то положим, что нам известно тригонометрическое представление числа w = r0(cos φ0 + i sin φ0), и будем искать число z также в тригонометрической форме: z = r(cos φ + i sin φ). Из определения аргумента и геометрической интерпретации комплексных чисел следует, что два комплексных числа, записанных в тригонометрической форме, равны тогда и только тогда, когда равны их модули, а аргументы отличаются на угол, кратный 2π. Имеем:  |
| откуда получается: |
Итак, все решения уравнения  задаются формулой
задаются формулой
Заметим, что если в эту формулу подставлять натуральные числа k, то при k = 0, 1, ..., n мы будем получать разные комплексные числа, а при k = n имеем:
Значит, и в дальнейшем значения корней будут повторяться. Следовательно, существует ровно n корней уравнения  и все они задаются одной формулой.
и все они задаются одной формулой.
Вторая формула Муавра:
Глава II. Практика. 2.1. Найти число, сопряженное к комплексному числу.
Найдите число, сопряжённое к комплексному числу (1 + 2i)(3 – 4i).
Решение:
| Имеем Следовательно,  Ответ. 11 – 2i. |
2.2. Найти модуль и аргумент комплексного числа.
Найти модуль и аргумент комплексного числа z = –1 – i.
Решение
| Так как Re z = –1 и Im z = –1, то точка z лежит в третьей координатной четверти. Для поиска аргумента решим систему Ответ. |
Глава III. Презентация.
ЗАКЛЮЧЕНИЕ
Комплексные числа это одно из фундаментальных понятий математического анализа. В данной работе мы изучили комплексные числа. Они играют значительную роль не только в математике, а также в таких науках, как физика, химия. В настоящее время комплексные числа активно используются в электромеханике, компьютерной и космической индустрии. Именно поэтому нам нужно расширять свои знания о комплексных числах, их свойствах и особенностях.
В зачетной работе я раскрыла понятие комплексного числа, операции над комплексными числами и тригонометрическая форма записи комплексного числа.
В практической работе решила примеры по комплексным числам и сделала презентацию.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
Андронов И.К. Математика действительных и комплексных чисел. – М., 2008г.
Гордиенко Н.А., Беляева Э.С., Фирстов В.Е., Серебрякова И.В. Комплексные числа и их приложения: Учебное пособие, 2008г.
Кураш А.Г. «Алгебраические уравнения произвольных степеней». М., 2007г.
Маркушевич А.И. «Комплексные числа и конформные отображения». М., 2009г.
Стройк Д.Я. «Краткий очерк истории математики». М., 2009г.
Яглом И.М. Комплексные числа и их приложения в геометрии. Изд. 2-е, стереотипное. – М., 2008г.
https://nsportal.ru/ap/library/drugoe/2014/01/14/referat-kompleksnye-chisla-ikh-proshloe-i-nastoyashchee
https://mathematics.ru/courses/algebra/content/chapter1/section4/paragraph1/theory.html#.XdAMMdIzbIU
http://mmmf.msu.ru/zaoch/math/complex.pdf
7







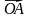 с координатами (a; b) на комплексной плоскости с началом в точке O (0; 0) и концом в точке A с координатами (a; b). Ясно, что это соответствие является взаимнооднозначным. В самом деле, как было только что отмечено, любому комплексному числу z = a + ib соответствует вектор
с координатами (a; b) на комплексной плоскости с началом в точке O (0; 0) и концом в точке A с координатами (a; b). Ясно, что это соответствие является взаимнооднозначным. В самом деле, как было только что отмечено, любому комплексному числу z = a + ib соответствует вектор 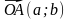 и наоборот, каждому вектору
и наоборот, каждому вектору 

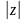 или r. Указанная в определении формула легко выводится при помощи теоремы Пифагора (Рисунок 3).
или r. Указанная в определении формула легко выводится при помощи теоремы Пифагора (Рисунок 3).
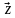 величина угла считается положительной, если угол отсчитывается против часовой стрелки, и отрицательным в противном случае.
величина угла считается положительной, если угол отсчитывается против часовой стрелки, и отрицательным в противном случае.