В ПОМОЩЬ СТУДЕНТУ-ЗАОЧНИКУ по дисциплине: «МАТЕМАТИКА» РАЗДЕЛ № 8 «Элементы математической статистики»

МИНИСТЕРСТВО ПРОСВЕЩЕНИЯ ПМР

ГОУ «ДНЕСТРОВСКИЙ ТЕХНИКУМ ЭНЕРГЕТИКИ

И КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ»

УТВЕРЖДАЮ

Зам. директора по учебной работе

__________________М.В. Питель

«_____»__________________2019 г

В ПОМОЩЬ СТУДЕНТУ-ЗАОЧНИКУ

по дисциплине: «МАТЕМАТИКА»

РАЗДЕЛ № 8

«Элементы математической статистики»

Разработал преподаватель математики

ГОУ СПО «ДТЭ и КТ»

Демьянова Светлана Васильевна

РАССМОТРЕНО СОГЛАСОВАНО

на заседании ЦМК методист

_____________________ дисциплин ________ Левицкая И.Н. Протокол №__ от «__»_____201__г. «__» _________201__г.

Председатель __________________

______________________________

г. Днестровск, 2019 г.

СОДЕРЖАНИЕ

Введение………………………………………………………………………………………………....3

Глава I. Элементы математической статистики…………………………………………………...4

1. Задача математической статистики………………………………………………………………...4

2. Генеральная и выборочная совокупность………………………………………………………….4
3. Статистическое распределение выборки и эмпирическая функция распределения……………5
4. Полигон и гистограмма……………………………………………………………………………..6

5. Эмпирическая функция распределения……………………………………………………………8

Глава II. Практика……………………………………………………………………………………..9

2.1. Найти относительные частоты………………….………………………………………………….9

2.2. Построить эмпирическую функцию………………………………………………………………9

Глава III. Презентация……………………………………………………………………………….11

Заключение………………………………………………………………………...…………………..12

Список использованной литературы………………………………………………………………13

ВВЕДЕНИЕ

В зачетной работе изложены основные теоретические разделы указанной темы, при этом особое внимание уделено основным элементам математической статистики и приведены примеры. Работа состоит из трех глав, традиционно изучаемых в курсе высшей математики, первая глава содержит пять подразделов, вторая два подраздела, и третья глава презентацию. Первая глава включает основные задачи математической статистики и раскрывает основные методы математической статистики. Второй главе приведены примеры математической статистики. Рассмотрим элементы математической статистики.

Глава I. Элементы математической статистики.

1. Задача математической статистики.

Задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.

Установление закономерностей, которым подчинены случайные явления, основано на изучении результатов наблюдений.

Первая задача математической статистики – указать способы сбора и группировки (если данных очень много) статистических сведений.

Вторая задача математической статистики – разработать методы анализа статистических данных в зависимости от целей исследования.

Изучение тех или иных явлении методами математической статистики служит средством решения многих вопросов, выдвигаемых наукой и практикой (правильная организация технологического процесса, наиболее целесообразное планирование и др.).

Применение идей и методов математической статистики сокращает объём экспериментальных исследований и, что самое главное, увеличивает четкость суждения исследователя об эксперименте.

1. Генеральная и выборочная совокупность.

Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить стандартность детали, а количественным — контролируемый размер детали.

Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов.

Генеральной совокупностью называют всю совокупность объектов, из которых производится выборка.

Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N = 1000, а объем выборки n = 100.

Часто генеральная совокупность содержит конечное число объектов. Однако, если это число достаточно велико, то иногда в целях упрощения вычислений или для облегчения теоретических выводов допускают, что генеральная совокупность состоит из бесчисленного множества объектов. Такое допущение оправдывается тем, что увеличение объема генеральной совокупности практически не сказывается на результатах обработки данных выборки.

Для того, чтобы по данным выборки можно было достаточно уверенно судить об интересующем нас признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно её представляли. Это требование коротко формулируют так: выборка должна быть репрезентативной (представительной).

Выборка будет репрезентативной, если ее осуществить случайно (т.е. если каждый объект выборки отобран случайно из генеральной совокупности) и если все объекты имеют одинаковую вероятность попасть в выборку.

1. Статистическое распределение выборки и эмпирическая функция распределения.

Пусть из генеральной совокупности извлечена выборка, причём x₁ наблюдалось n₁ раз, х₂ – n₂ раз, x_k – n_k раз и n_i = n – объём выборки. Наблюдаемые значения x_i называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом. Числа наблюдений называют частотами, а их отношения к объему выборки 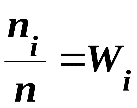 –относительными частотами.

Статическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).

Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике – соответствие между наблюдаемыми вариантами и их частотами или относительными частотами.

Эмпирической функцией распределения (функцией распределения выборки) называют функцию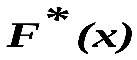 , определяющую для каждого значения х относительную частоту события X х

,

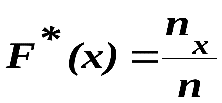где 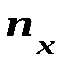  – число вариант, меньших х,

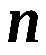–объем выборки.

Таким образом, для того чтобы найти, например,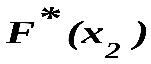 , надо число вариант, меньших  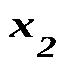, разделить на объем выборки

.

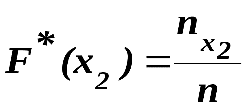В отличие от эмпирической функции распределения выборки интегральную функцию 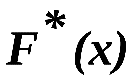  распределения генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция  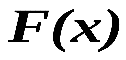 определяет вероятность события X х, а эмпирическая  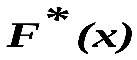 – определяет относительную частоту этого же события. Согласно теореме Бернулли, относительная частота события Х х, т.е.  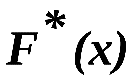 стремится по вероятности к вероятности  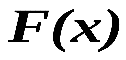 этого события. Другими словами, числа  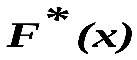 и 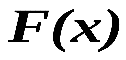  мало отличаются друг от друга. Отсюда следует целесообразность использования эмпирической функции распределения выборки для приближенного представления теоретической (интегральной) функции распределения генеральной совокупности.

Из определения функции 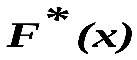  вытекают следующие ее свойства:

• значения эмпирической функции принадлежат отрезку [0,1];

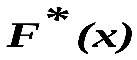• –неубывающая функция;

• если x₁ – наименьшая варианта, то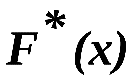  = 0 при х  x₁;

• если x_k – наибольшая варианта, то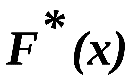  = 1 при х  х_k.

Итак, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.

1. Полигон и гистограмма.

В целях наглядности строят различные графики статистического распределения и, в частности, полигон и гистограмму.

Полигоном частот называют ломаную, отрезки которой соединяют точки (x₁, n₁), (x₂, n₂), ..., (x_k, n_k). Для построения полигона частот на оси абсцисс откладывают варианты х_i, а на оси ординат – соответствующие им частоты n_i. Точки (x_i, n_i) соединяют отрезками прямых и получают полигон частот.

Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (x₁, W₁), (x₂, W₂),..., (x_k, W_k). Для построения полигона относительных частот на оси абсцисс откладывают варианты x_i, a на оси ординат соответствующие им относительные частоты W_i.

Точки (x_i, W_i) соединяют отрезками прямых и получают полигон относительных частот (рис. 1).

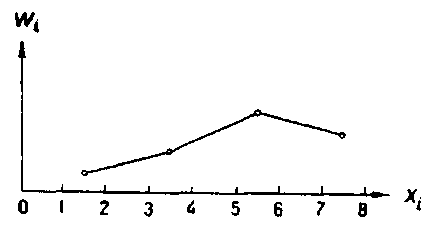
Рис. 1.

В ряде случаев, в частности, в случае непрерывного признака, целесообразно строить гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиною h и находят для каждого частичного интервала n_i, т.е. сумму частот вариант, попавших в i-й интервал.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению 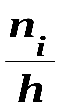 (плотность частоты). Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии  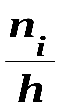 . Площадь i-гo частичного прямоугольника равна  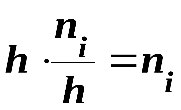 сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению 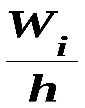 (плотность относительной частоты). Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии  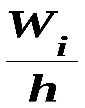(рис. 2). Площадь i-го частичного прямоугольника равна  – относительной частоте вариант, попавших вi-й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.

Рис.2

1. Эмпирическая функция распределения.

Определение. Пусть дана выборка объема n. Для любого числа x вычислим k_х – количество элементов в выборке со значением меньшим, чем x.

Эмпирическая функция распределения определяется по формуле:

Глава II. Практика.

2.1. Найти относительные частоты.

Задано распределение частот выборки объема n = 20:

Решение. Найдем относительные частоты, для чего разделим частоты на объем выборки:

,  ,  .

Напишем распределение относительных частот:

Контроль: 0,15 + 0,5 + 0,35 = 1.

2.2. Построить эмпирическую функцию.

Построить эмпирическую функцию по данному распределению выборки:

Решение. Найдем объем выборки: 12 + 18 + 30 = 60. Наименьшая варианта равна 2, следовательно,

= 0 при х  2.

Значение Х x₁ = 2 наблюдалось 12 раз, следовательно,

при 2 x  6.

Значения Х x₁ = 2 и x₂ = 6 наблюдались 12 + 18 = 30 раз, следовательно,

при 6  x  10.

Так как х = 10 – наибольшая варианта, то

= 1 при х  10.

Искомая эмпирическая функция

График функции

Глава III. Презентация.

ЗАКЛЮЧЕНИЕ

Элементы математической статистики одно из фундаментальных понятий математического анализа. В данной работе мы изучили элементы математической статистики. В зачетной работе я раскрыла задачи математической статистики, генеральная и выборочная совокупность, статистическое распределение выборки и эмпирическая функция распределения, полигон и гистограмма, эмпирическая функция распределения.

В практической работе решила примеры по элементам математической статистики и сделала презентацию.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Балдин, К.В. Теория вероятностей и математическая статистика, М. 2016г.

2. Буре, В.М. Теория вероятностей и математическая статистика, 2013г.

3. Романова, Е.С. Теория вероятностей и математическая статистика, 2013г.

4. Семенов, В.А. Теория вероятностей и математическая статистика: Учебное пособие, 2013г.

5. Яковлев, В.П. Теория вероятностей и математическая статистика: Учебное пособие, 2012г.

6. https://docplayer.ru/58994529-Lekciya-1-vvedenie-osnovnye-ponyatiya-i-metody-matematicheskoy-statistiki.html

7. https://studfile.net/preview/5227216/page:9/

8. https://vlgr.ranepa.ru/pp/hmp/pl200/lec2k_05.pdf

12