|   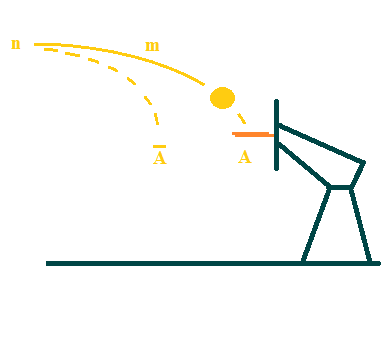 Рис.1
Для расчёта числа возможных событий используются методы комбинаторики. Число комбинаций из n элементов по m, которые отличаются только составом элементов называются сочетаниями. Например: число сочетаний из n элементов по m рассчитывается по следующей формуле: 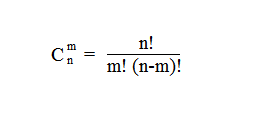
Число комбинаций, которые отличаются и составом, и расположением называются размещениями. Число размещений из n элементов по m рассчитывается так: 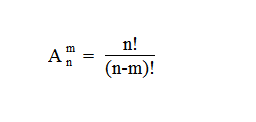
Число комбинаций из n элементов, которые отличаются только перестановкой равно: 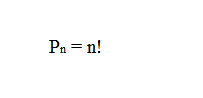
Комбинации из n элементов по m, в которых элементы могут быть одинаковыми, называются размещениями с повторениями. Число таких размещений рассчитывается по следующей формуле: 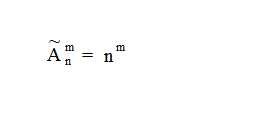
Число сочетаний с повторениями из n элементов по m рассчитывается: 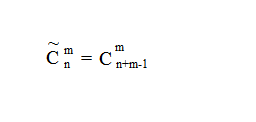
Допустим, что комбинации состоят из n элементов. 1-й элемент повторяется n1 раз, 2-й элемент n2 раз и k-й элемент nk раз, при этом n1 + n2 + ... nk = n. Такие комбинации называются перестановки с повторениями. Число таких перестановок рассчитывается так: 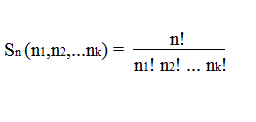
Комбинация событий. Противоположные события. Суммой (объединением) событий A и B называется событие, которое состоит в том, что происходит хотя бы одно из данных событий. Сумму событий A и B обозначают A+B (или A∪B). На рисунке 2 с помощью кругов Эйлера проиллюстрировано понятие суммы событий A и B: большой круг изображает все элементарные события, которые могут произойти в рассматриваемом испытании, левый круг изображает событие A, правый — событие B, а закрашенная область — A+B событие. 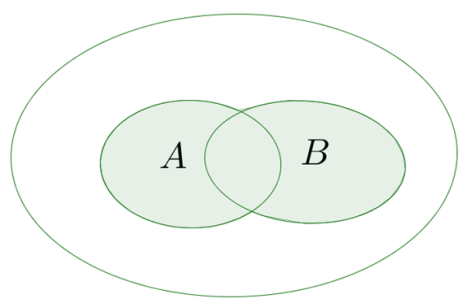
Рис.2 Произведением (пересечением) событий A и B называется событие, которое состоит в том, что происходят оба эти события. Произведение событий A и B обозначают AB (или A∩B). Рисунок 3 иллюстрирует с помощью кругов Эйлера произведение событий A и B: темнее закрашенная область (общая часть кругов A и B) иллюстрирует событие AB. 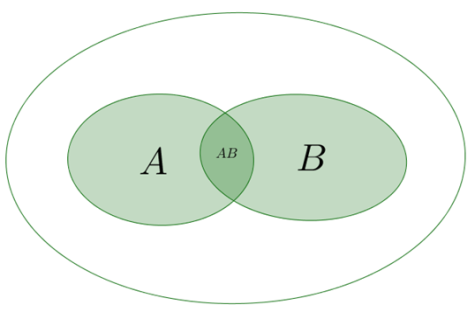
Рис.3 События A и B называют равными (равносильными) и пишут A=B, если событие A происходит тогда и только тогда, когда происходит событие B. Событие 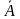 называют противоположным событию A, если событие называют противоположным событию A, если событие 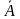 происходит тогда и только тогда, когда не происходит событие A. происходит тогда и только тогда, когда не происходит событие A. На рисунке 4 проиллюстрирована взаимосвязь событий A и 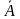 на множестве всех элементарных исходов испытания (событие на множестве всех элементарных исходов испытания (событие 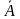 изображено закрашенной областью). изображено закрашенной областью). 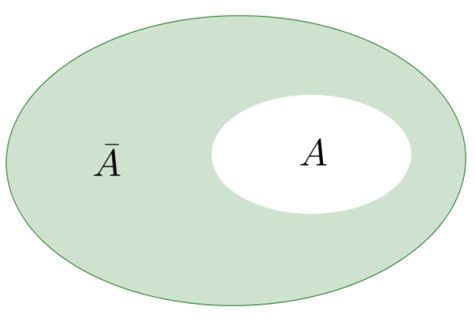
Рис.4 Вероятность противоположного события. Если все исходы опыта одинаково возможны, то вероятность P(A) любого события A можно вычислить по формуле: 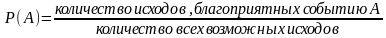
Вероятность противоположного события можно вычислить по формуле: P(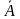 )=1−P(A). )=1−P(A).
Бросается игровой кубик. Событие A — выпадет цифра 2. Ранее уже было вычислено, что P(A)= 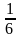 . . Противоположное событие 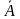 — не выпадет цифра 2 (т. е. выпадет 1, 3, 4, 5 или 6). — не выпадет цифра 2 (т. е. выпадет 1, 3, 4, 5 или 6). P(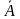 )=1−P(A)=1− )=1−P(A)=1−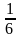 = =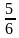 . . Эту формулу удобно использовать, если у опыта много исходов.
Сложение вероятности. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий, т. е. P(A+B) = P(A)+P(B). События являются несовместными, или несовместимыми если появление одного из них исключает появление другого.
Независимые события. Умножение вероятностей.
Предположим, что из колоды в 36 карт извлекается одна карта и рассматриваются: событие A — извлечена карта трефовой масти, событие B — извлечена дама треф. Между событиями A и B очевидно наличие какой-то зависимости. Действительно, из 9 случаев, благоприятствующих событию A, событию B благоприятствует один; поэтому при наступлении события A вероятность события B равна 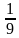 . Но при отсутствии информации о наступлении события A вероятность события B оценивается как равная . Но при отсутствии информации о наступлении события A вероятность события B оценивается как равная 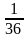 . Так как . Так как 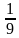 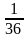 , то очевидно, что наступление события A повышает шансы события B. , то очевидно, что наступление события A повышает шансы события B. События A и B называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие A называется зависимым от события B, если вероятность события A меняется в зависимости от того, произошло событие B или нет. Часто о независимости событий удаётся судить на основании того, как организован опыт, в котором они происходят. Независимые события появляются тогда, когда опыт состоит из нескольких независимых испытаний (как, например, было в рассмотренном опыте с бросанием двух игральных костей). Если независимость испытаний не очевидна, то независимость событий A и B проверяется с помощью формулы: события A и B называют независимыми, если выполняется равенство P(AB)=P(A)⋅P(B).
Статистическая вероятность. Проведём эксперимент: 1) бросить игровой кубик 200 раз и каждый раз записывать количество выпавших пунктов; 2) сосчитать, в скольких случаях выпало 4 пункта. Допустим, что после подсчётов результат 4 был 32 раза. Что можно вычислить? Если в N независимых опытах событие A осуществляется M раз, то M называется абсолютной частотой события A, а соотношение  называется относительной частотой события A. называется относительной частотой события A. Относительную частоту события A обозначают W(A), поэтому по определению W(A)= . . В наших экспериментах событие A — выпали 4 пункта. Значит, по определению: 1) абсолютная частота события A равна 32; 2) относительная частота события А= . . Статистической вероятностью называют число, около которого колеблется относительная частота события при большом числе испытаний. Различные исследования с большим числом однотипных испытаний проводили учёные в разные годы. Наблюдая за уменьшением амплитуды колебания относительных частот события около некоторого числа при увеличении количества испытаний, швейцарский математик Якоб Бернулли обосновал так называемый закон больших чисел. Можно считать достоверным тот факт, что при любой достаточно большой серии испытаний относительная частота события А стремится к некоторому числу — вероятности этого события. Таким образом, W(A)≈P(A) при большом числе испытаний. В нашем эксперименте относительная частота события А= , или статистическая вероятность P(A)≈ , или статистическая вероятность P(A)≈ . .
| 









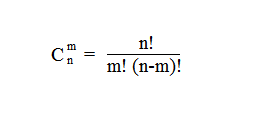
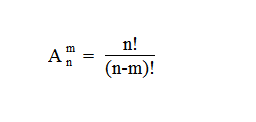
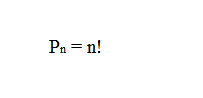
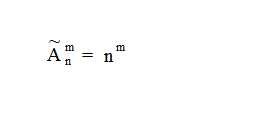
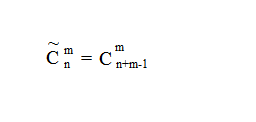
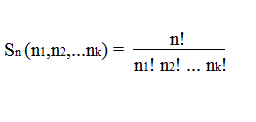


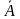 называют противоположным событию A, если событие
называют противоположным событию A, если событие 
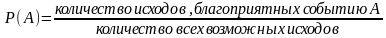
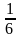 .
.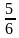 .
.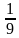 . Но при отсутствии информации о наступлении события A вероятность события B оценивается как равная
. Но при отсутствии информации о наступлении события A вероятность события B оценивается как равная 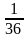 . Так как
. Так как 









