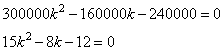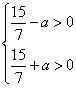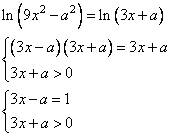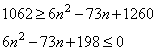Вариант 4. ЕГЭ 2021 11 класс Профиль.Решение

Вариант 4. ЕГЭ 2021 11 класс Профиль.Решение

Задание 1. Держатели дисконтной карты книжного магазина получают при покупке скидку 6%. Книга стоит 650 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?

Решение.

Скидка 6% означает, что за книгу нужно заплатить 100-6=94%. Так как книга стоит 650 рублей, получаем стоимость со скидкой, равной

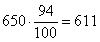 рублей.

Ответ: 611.

Задание 2. На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту, на оси ординат — крутящий момент в Н∙м. Какое число оборотов в минуту должен совершать двигатель, чтобы крутящий момент был не менее 60 Н∙м?

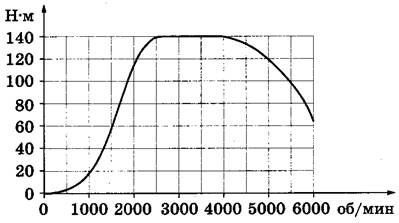
Решение.

Так как по оси Oy отложен крутящий момент, то смотрим требуемый уровень 60 Н∙м по этой оси. Этому уровню по оси Ox соответствует число оборотов двигателя, равное 1500 об/мин (см. красные линии на рисунке ниже).

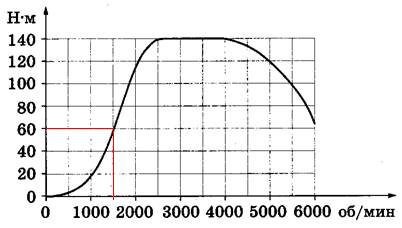
Ответ: 1500.

Задание 3. На клетчатой бумаге с размером клетки 1x1 изображена трапеция. Найдите длину средней линии этой трапеции.

Решение.

Длина средней линии трапеции находится по формуле

,

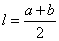где a – длина верхнего основания трапеции; b – длина нижнего основания трапеции. Из рисунка видно, что a=3, b=4 и длина средней линии

.

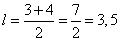Ответ: 3,5.

Задание 4. В среднем из 1800 садовых насосов, поступивших в продажу, 18 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

Решение.

Обозначим через событие А то, что случайно выбранный насос не подтекает. Число благоприятных исходов для события А равно 1800-18=1782, всего исходов 1800, получаем вероятность события А:

.

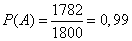Ответ: 0,99.

Задание 5. Найдите корень уравнения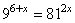 

Решение.

Число 81 можно представить как 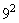 , следовательно,  . Получаем следующее уравнение:

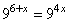
и, так как основания у степеней равны, то переходим к равенству самих степеней:

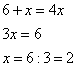
Ответ: 2.

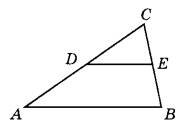
Задание 6. Площадь треугольника ABC равна 8. DE — средняя линия. Найдите площадь треугольника CDE.

Решение.

Известно, что длина средней линии DE треугольника ABC равна половине основания AB, которому она параллельна. Также точки D и E средней линии лежат посередине отрезков AC и CB соответственно. Следовательно, стороны треугольника CDE в 2 раза меньше соответствующих сторон треугольника ABC. Тогда площадь треугольника CDE будет в 4 раза меньше площади треугольника ABC и равна 8:4 = 2.

Ответ: 2.

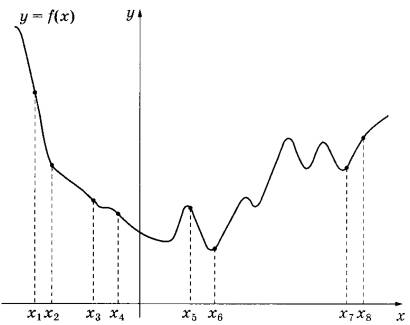
Задание 7. На рисунке изображён график функции у = f(x) и восемь точек на оси абсцисс: x1, х2, х3, х4, х5, x6, x7, х8. В скольких из этих точек производная функции f(x) отрицательна?

Решение.

Производная отрицательна на отрезках, в которых функция f(x) убывает. Следовательно, нужно выбрать все точки, где функция f(x) убывает, имеем: 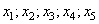 , то есть 5 точек.

Ответ: 5.

Задание 8. Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 28. Найдите объём цилиндра.

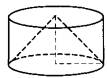
Решение.

Известно, что объем конуса определяется формулой

,

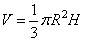где H – высота конуса; R – радиус основания конуса. Объем же цилиндр можно найти как

,

то есть в 3 раза больше объема конуса и равен:

.

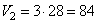Ответ: 84.

Задание 9. Найдите 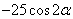 , если  .

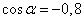Решение.

Преобразуем косинус двойного угла следующим образом:

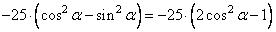
и подставим значение 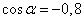 , получим:

.

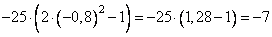Ответ: -7.

Задание 10. В розетку электросети подключены приборы, общее сопротивление которых составляет R1=56 Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление R2 этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями R1 и R2 их общее сопротивление задаётся формулой 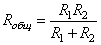 , а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 24 Ом. Ответ дайте в омах.

Решение.

В задании дано значение сопротивления R1=56 Ом и необходимо подобрать такое минимальное значение R2, чтобы общее сопротивление было равно 24 Ом. Получаем следующее уравнение:

,

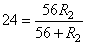откуда

То есть минимальное сопротивление R2 составляет 42 Ом.

Ответ: 42.

Задание 22. Расстояние между пристанями А и В равно 90 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот проплыл 52 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.

Решение.

Пока лодка шла из точки A в точку B и обратно, плот по течению реки проплыл 52 км. Учитывая скорость течения реки 4 км/ч, получаем время движения плота 52:4=13 часов. Так как лодка отправилась вслед за ним только через час, то ее время в пути будет равно 13-1=12 часов. Обозначим теперь через x км/ч собственную скорость лодки. Из пункта A в B она шла по течению, то есть со скоростью x+4 км/ч и путь в 90 км составил   часов. Обратно она шла против течения и тот же путь проделала за 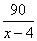  часа. Все время пути равно 12 часов. Получаем уравнение:

,

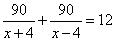упрощаем, имеем:

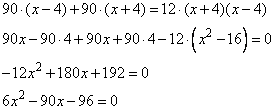
Решаем квадратное уравнение через дискриминант, получаем:

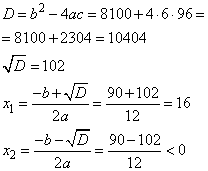
Так как собственная скорость лодки не может быть отрицательной величиной, получаем значение 16 км/ч.

Ответ: 16.

Задание 12. Найдите точку минимума функции y = x – ln(x+6) + 3.

Решение.

1. ОДЗ  .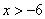

2. Найдем точки экстремума функции. Для этого вычислим ее производную и приравняем ее нулю, получим:

,

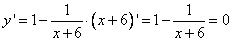откуда

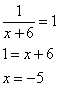
Имеем одну точку экстремума x=-5, в которой функция принимает минимальное значение, так как производная в окрестности этой точки меняет свой знак с «-» на «+».

Ответ: -5.

Задание 13. а) Решите уравнение  .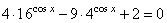

б) Найдите все корни этого уравнения, принадлежащие отрезку  .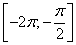

Решение.

а) Пусть 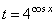 , тогда уравнение запишется в виде

.

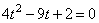Решаем квадратное уравнение, получаем два корня:

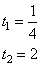
При t=1/4, получаем:

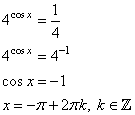
При t=2, получаем:

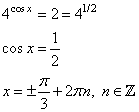
б) С помощью числовой окружности отберём корни, принадлежащие отрезку  .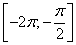

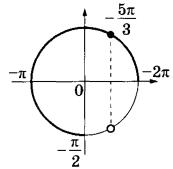
Получаем корни  .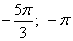

Примечание: эти же корни также можно найти с помощью неравенств, используя инструмент tools.self-edu.ru.

Ответ: а) 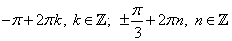 ; б)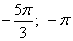 

Ответ задания: а) 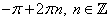 ;  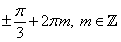; б)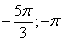 

Задание 14. На ребре SA правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка М, причём SM : МА = 5:1. Точки P и Q — середины рёбер ВС и AD соответственно.

а) Докажите, что сечение пирамиды плоскостью MPQ является равнобедренной трапецией.

б) Найдите отношение объёмов многогранников, на которые плоскость MPQ разбивает пирамиду.

Решение.

а) Пусть N — такая точка на ребре SB, что SN:NB = 5:1. Треугольники SAB и SMN подобны по двум пропорциональным сторонам и углу между ними. Значит,  , а прямые AB и MN параллельны, 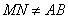 . Прямая PQ также параллельна прямой АВ. Значит, отрезки MN и PQ параллельны и не равны, и поэтому сечение пирамиды плоскостью MPQ — это трапеция MNPQ.

Треугольники MAQ и NBP равны, поскольку MA = NB, QA = PB, и 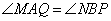 , поэтому MQ = NP, а значит, трапеция MNPQ равнобедренная.

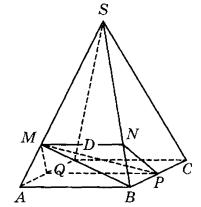
б) Пусть объём пирамиды SABCD равен V. Пятигранник AMQBNP состоит из четырёхугольной пирамиды MABPQ с основанием ABPQ и треугольной пирамиды MBNP с основанием BNP.

Расстояние от точки М до плоскости BNP относится к расстоянию от точки A до этой плоскости как 5:6, а площади треугольников BNP и SBC относятся как 1:12. Значит, отношение объёмов пирамид MBNP и ASBC равно 5:72, то есть объём пирамиды MBNP равен  .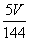

Площадь прямоугольника ABPQ составляет половину площади квадрата ABCD. Расстояние от точки М до плоскости ABCD относится к расстоянию от точки S до этой плоскости как 1: 6, поэтому объём пирамиды MABPQ равен  .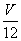

Таким образом, объём AMQBNP равен 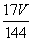  то есть отношение объёмов многогранников AMQBNP и CDSNPQM равно 17 : 127.

Ответ: 17 : 127.

Задание 15. Решите неравенство  .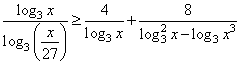

Решение.

Пусть 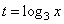 , тогда неравенство примет вид:

Откуда t 3.

При t

,

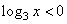откуда 0

При t = 2 получим:

,

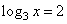откуда x = 9.

При t 3 получим:

,

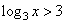откуда x 27. Решение исходного неравенства:

.

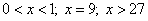Ответ:  .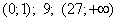

Задание 16. В трапеции ABCD основание AD в два раза меньше основания ВС. Внутри трапеции взяли точку М так, что углы ВАМ и CDM прямые.

а) Докажите, что ВМ = СМ.

б) Найдите угол ABC, если угол BCD равен 64°, а расстояние от точки М до прямой ВС равно стороне AD.

Решение.

а) Пусть прямые АВ и CD пересекаются в точке L. Тогда треугольники BLC и ALD подобны с коэффициентом подобия 2, поскольку ВС = 2AD. Значит, А и D — середины BL и CL соответственно. Таким образом, AM и DM — серединные перпендикуляры в треугольнике BLC, а М — центр описанной около этого треугольника окружности, поэтому BM = CM как радиусы этой окружности.

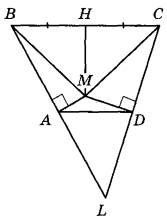
б) Пусть Н — середина ВС, тогда МН — серединный перпендикуляр к стороне ВС. Значит, треугольники ВНМ и СНМ равнобедренные прямоугольные, поэтому 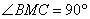 . По свойству вписанного угла

,

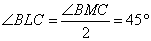откуда

.

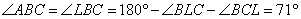Ответ: 71.

Задание 17. В июле 2020 года планируется взять кредит в банке на сумму 300 000 рублей. Условия его возврата таковы:

- каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;

- с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.

Найдите r, если известно, что кредит будет полностью погашен за два года, причём в первый год будет выплачено 160 000 рублей, а во второй год — 240 000 рублей.

Решение.

Изначально была взята сумма долга, равная 300 000 рублей. По условию задачи сначала сумма долга увеличивается на r%, то есть в 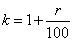  раз, получаем сумму 300000∙k. После этого, вносится платеж, равный 160 000 рублей. Остаток суммы долга становится равным

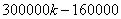 рублей.

В следующем году остаток также увеличивается в k раз

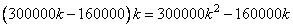
и вносится сумма в 240 000 рублей:

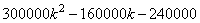 рублей.

По условию задачи за два года долг полностью гасится, то есть, имеем:

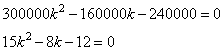
Решаем квадратное уравнение, получаем два корня:

Имеем один положительный корень 6/5 (отрицательный не берется, так как ставка по кредиту не может быть отрицательной). В результате получаем:

Таким образом, кредит планируется взять под 20% годовых.

Ответ: 20.

Задание 18. Найдите все значения а, при каждом из которых уравнение

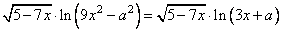
имеет ровно один корень.

Решение.

Исходное уравнение равносильно уравнению:

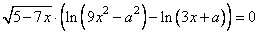
Рассмотрим два случая. Первый случай:

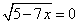 при условии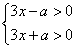 

Получаем 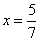 . Условие принимает вид:

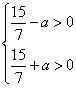
откуда

.

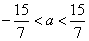То есть в этом случае 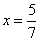  при  .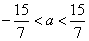

Второй случай:

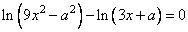
при условии  . Получаем:

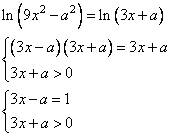
откуда 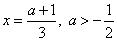 . Условие принимает вид:

,

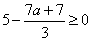откуда 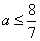 . То есть в этом случае  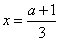 при  .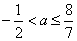

Корни уравнения 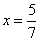  и 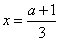  совпадают при  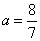. Таким образом, исходное уравнение имеет ровно один корень пр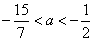и   и  .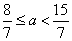

Ответ:  .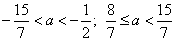

Задание 19. На доске написано 35 различных натуральных чисел, каждое из которых либо чётное, либо его десятичная запись оканчивается на цифру 3. Сумма написанных чисел равна 1062.

а) Может ли на доске быть ровно 27 чётных чисел?

б) Могут ли ровно два числа на доске оканчиваться на 3?

в) Какое наименьшее количество чисел, оканчивающихся на 3, может быть на доске?

Решение.

а) Например, следующий набор чисел удовлетворяет условию задачи:

3, 13, 23, 33, 43, 53, 63, 73, 2, 4, ..., 50, 52, 56.

б) Пусть на доске написано ровно два числа, оканчивающихся на 3. Тогда на доске 33 чётных числа. Их сумма не меньше, чем сумма 33 наименьших чётных чисел:

.

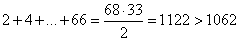Это противоречит тому, что сумма написанных чисел равна 1062.

в) Пусть на доске написано n чисел, оканчивающихся на 3, и 35-n чётных чисел. Тогда сумма чисел, оканчивающихся на 3, не меньше

,

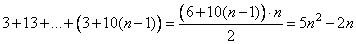а сумма чётных чисел не меньше

.

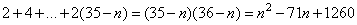Таким образом,

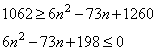
откуда, учитывая, что n — целое, получаем  .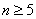

Если на доске написано пять чисел, оканчивающихся на 3, и 30 чётных чисел, то их сумма нечётна. Значит, чисел, оканчивающихся на 3, больше пяти.

Приведём пример шести чисел, оканчивающихся на 3, и 29 чётных чисел, сумма которых равна 1062:

3, 13, 23, 33, 43, 53, 2, 4, ..., 54, 56, 82.

Ответ: а) да; б) нет; в) 6.

.
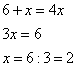
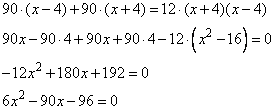
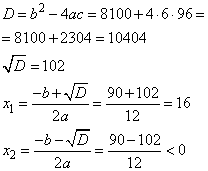
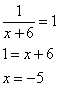
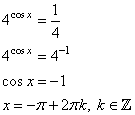
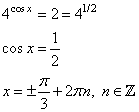
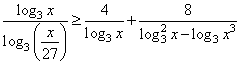