Векторно-координатный метод – это частный случай метода математического моделирования, в рамках которого решаемая задача (доказываемая теорема), переводится на векторно-координатный язык. Основные этапы применения векторно-координатного метода:
перевод задачи на язык векторно-координатных соотношений (получение вспомогательной задачи):
выбрать наиболее подходящую систему координат,
ввести вектора и определить их координаты,
перевести условия задачи на язык векторно-координатных соотношений;
решение задачи векторной алгебры с использованием знаний о координатах введенных векторов (решение вспомогательной задачи);
перевод результата решения на язык исходной задачи.
Заметим, что различия между векторным и векторно-координатным методом проявляются лишь на уровне их подструктуры. Цели основных этапов (обозначенных цифрами) одинаковы для обеих разновидностей метода, однако, цели входящих в них действий совпадают не везде.
Рассмотрим виды задач, которые могут быть решены векторно-координатным методом.
Аффинные и метрические геометрические задачи.
Сведения, которые получают учащиеся о векторах на уроках геометрии, можно разделить на две группы. К первой относят: определение вектора, операции сложения и вычитания векторов и их свойства, понятия коллинеарности и компланарности векторов, операция умножения вектора на число и её свойства, разложение вектора в данном базисе, единственность такого разложения. Ко второй группе относят: скалярное умножение векторов и его алгебраические свойства. Первая группа фактов позволяет решать обширный круг задач на параллельность, нахождение отношения длин параллельных отрезков, на гомотетию, принадлежность трёх точек одной прямой, четырёх точек одной плоскости. Вторая группа фактов эффективна для вычисления расстояний, углов, доказательства неравенств, нахождение геометрических мест точек.
Задачи первого типа называются аффинными, второго типа – метрическими. В ходе применения векторов к решению задач учащиеся постепенно должны усвоить следующее: посредством операций сложения векторов, умножения вектора на число вычислять расстояния и углы не удаётся. Поэтому эти операции, как правило, неприменимы в задачах, в которых фигурирует такие понятия как окружность, биссектриса, перпендикуляр. Но задачи, в которых идёт речь о параллельных прямых и плоскостях, параллельных отрезках (конкретно о параллелограмме, трапеции, параллелепипеде, призме, середине отрезка, средней линии треугольника, центральной симметрии, точке пересечения медиан треугольника и тетраэдра), поддаются эффективному решению.
Рассмотрим решения аффинных задач трёх типов. К первому типу отнесём задачи, в условиях которых не фигурируют векторы и при решении которых не требуется прибегать к векторному заданию множества точек. Ко второму – задачи на доказательство и вычисление, для решения которых требуется рассматривать векторно-параметрическое задание прямой и плоскости. Задачи третьего типа отличаются тем, что в их содержании уже включены векторы.
Эти типы задач далеко не исчерпывают всего многообразия аффинных задач. Но они образуют самые многочисленные группы задач, что и оправдывает их специальное рассмотрение.
Пример 1.1
Доказать, что три точки  ,
,  и
и  лежат на одной прямой.
лежат на одной прямой.
Доказательство.
Рассмотрим треугольник ABC, с вершинами в указанных точках. Если все три точки лежат на одной прямой, то можем утверждать, что площадь треугольника должна быть равна нулю.
Согласно формуле площади треугольника

и условию, что  , получим
, получим
 ,
,
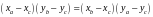 .
.
Преобразуем полученное выражение к виду
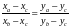
Подставим в данное равенство известные координаты точек
 ,
,
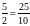 ,
,
 .
.
Получили верное равенство, и можем сделать вывод, что три данные точки  ,
,  и
и  лежат на одной прямой, что требовалось доказать.
лежат на одной прямой, что требовалось доказать.
Пример 1.2
Выяснить, параллельны ли прямые  и
и  ?
?
Решение.
Сначала запишем оба уравнения в общем виде уравнения прямой:
a:  ,
,
b:  .
.
Отсюда получаем 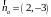 и
и 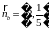 .
.
Проверим условие 
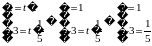 .
.
Эти векторы не коллинеарны, так как не существует такого 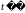 , для которого верно равенство
, для которого верно равенство  . Следовательно, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые a и b не параллельны.
. Следовательно, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые a и b не параллельны.
Ответ: прямые  и
и  не параллельны.
не параллельны.
Пример 1.3
Выяснить, являются ли прямые  и
и  параллельными?
параллельными?
Решение.
Преобразуем уравнение второй прямой и запишем в общем виде:

a:  ,
,
b:  .
.
Отсюда получаем  и
и  .
.
Проверим условие  , для этого вычислим скалярное произведение нормального вектора прямой a и направляющего вектора прямой b
, для этого вычислим скалярное произведение нормального вектора прямой a и направляющего вектора прямой b
.
Отсюда делаем вывод, что векторы  и
и  перпендикулярны, а значит прямые a и b параллельны.
перпендикулярны, а значит прямые a и b параллельны.
Проверим, чтобы прямые a и b не совпадали, для этого выберем точку  , принадлежащую первой прямой, и подставим ее в уравнение второй прямой
, принадлежащую первой прямой, и подставим ее в уравнение второй прямой  . Получаем, что прямые не совпадают и параллельны.
. Получаем, что прямые не совпадают и параллельны.
Ответ: прямые  и
и  являются параллельными.
являются параллельными.
Пример 1.4
Доказать, что прямые  и параллельны.
и параллельны.
Доказательство.
Введем обозначение:
a: 
b: .
Чтобы доказать параллельность прямых, необходимо показать коллинеарность направляющих векторов.
Получаем  и
и  .
.
Проверим условие 
. Значит,  .
.
Векторы  и
и  коллинеарны, так как существует такой
коллинеарны, так как существует такой 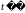 , для которого верно равенство
, для которого верно равенство  . Значит, выполняется необходимое и достаточное условие параллельности прямых в пространстве. Следовательно, заданные прямые
. Значит, выполняется необходимое и достаточное условие параллельности прямых в пространстве. Следовательно, заданные прямые  и параллельны, что требовалось доказать.
и параллельны, что требовалось доказать.
Пример 1.5
Найти координаты точки C, которая делит отрезок AB если известны координаты радиус-векторов  и
и  в отношении 5:3.
в отношении 5:3.
Решение.
По условию дано , значит
, значит  .
.
Воспользуемся ранее полученными формулами для нахождения точки С
.
Получаем координаты искомой точки  .
.
Ответ:  .
.
Пример 1.6
Найти координаты точки A, если известно, что точка С делит отрезок AB в отношении 1:3, а координаты радиус-векторов  и
и  .
.
Решение.
По условию дано , значит
, значит  .
.
Воспользуемся ранее полученными формулами для нахождения точки С и выразим из них координаты точки A.
.
Подставим известные значения
.
Получаем координаты искомой точки  .
.
Ответ:  .
.
Класс метрических задач шире класса задач с аффинным содержанием. Их типы можно выделить по виду требования: вычисление расстояний, вычисление углов, нахождение ГМТ, получение геометрических неравенств.
Пример 1.7
Проверить, перпендикулярны ли прямые AB и AC, если в декартовой (прямоугольной) системе координат известны точки  ,
,  и
и  .
.
Решение.
Векторы  и
и  лежат на прямых AB и AC, а значит, являются их направляющими векторами соответственно.
лежат на прямых AB и AC, а значит, являются их направляющими векторами соответственно.
Зная координаты точек, найдем координаты векторов:


Проверим условие 
.
Отсюда делаем вывод, что векторы  и
и  перпендикулярны, а значит прямые AB и AC перпендикулярны.
перпендикулярны, а значит прямые AB и AC перпендикулярны.
Ответ: прямые AB и AC перпендикулярны.
Пример 1.8
Найти расстояние от точки  до прямой
до прямой  .
.
Решение.
Обозначим имеющуюся прямую
a:  .
.
Найдем уравнение прямой b, перпендикулярной прямой a и проходящей через данную точку M.
Нормальный вектор прямой a перпендикулярен самой прямой, и он же является направляющим вектором прямой b.
Нормальный вектор:  , тогда направляющий вектор:
, тогда направляющий вектор:  .
.
Зная координаты точки, через которую проходит прямая и координаты ее направляющего вектора составим каноническое уравнение прямой b.
 и перейдем к общему уравнению прямой
и перейдем к общему уравнению прямой

b:  .
.
Найдем координаты точки N пересечения прямых a и b, для этого решим систему уравнений:
.
Получили точку  .
.
Длина отрезка MN будет искомым расстоянием от точки M до прямой a.
.
Ответ: расстояние от точки  до прямой
до прямой  равно 5.
равно 5.
Пример 1.9
Найти угол между скрещивающимися прямыми  и
и  , уравнения которых определены в декартовой (прямоугольной) системе координат.
, уравнения которых определены в декартовой (прямоугольной) системе координат.
Решение.
Введем обозначение
a:  ,
,
b:  .
.
Отсюда получаем направляющие векторы  и
и  .
.
Воспользуемся формулой, представленной выше, и вычислим
Ответ: угол между скрещивающимися прямыми  и
и  равен
равен  .
.
Рассмотренные примеры решению геометрических задач, позволяют увидеть основные эвристики, лежащие в основе применения векторно-координатного метода.
Алгебраические задачи, решаемые векторно-координатным методом
Векторно-координатный метод может быть успешно применен при изучении некоторых вопросов школьного курса алгебры: решение уравнений и неравенств, доказательство тождеств и неравенств, решение задач на оптимизацию.
Пример 1.10
Решить уравнение  .
.
Решение.
Оценим область допустимых значений
Введем два вектора  и
и  .
.
Вычислим скалярное произведение этих векторов
 . Обратим внимание, что получили левую часть исходного уравнения.
. Обратим внимание, что получили левую часть исходного уравнения.
Найдем значения длин этих векторов
 .
.
Произведение длин векторов  совпадает с правой частью исходного уравнения.
совпадает с правой частью исходного уравнения.
Получили, что скалярное произведение векторов равно произведению их длин, значит, угол между этими векторами равен 0 и они сонаправлены.
Известно, что координаты сонаправленных векторов пропорциональны, откуда получаем равенство
 .
.
Это уравнение можем решить



 .
.
 или
или 
Все три корня удовлетворяют области допустимых значений.
Ответ:  ;
;  .
.
Пример 1.11
Решить систему уравнение .
Решение.
Оценим область допустимых значений
Введем два вектора  и
и  .
.
Вычислим скалярное произведение этих векторов
 . Обратим внимание, что получили левую часть второго уравнения системы.
. Обратим внимание, что получили левую часть второго уравнения системы.
Найдем значения длин этих векторов
 , из первого уравнения следует
, из первого уравнения следует 
.
Произведение длин векторов  совпадает с правой частью второго уравнения системы.
совпадает с правой частью второго уравнения системы.
Получили, что скалярное произведение векторов равно произведению их длин, значит, угол между этими векторами равен 0 и они сонаправлены.
Известно, что координаты сонаправленных векторов пропорциональны, откуда получаем равенство
 .
.
Преобразуем это уравнение
 .
.
Отсюда можем делать вывод, что  .
.
Вернемся к первому уравнению системы



 .
.
Учитывая область допустимых значений, получаем .
.
Ответ:  .
.
Пример 1.12
Решить неравенство  .
.
Решение.
Оценим область допустимых значений
Введем два вектора  и
и  .
.
Вычислим сумму этих векторов
 .
.
Найдем значения длин этих векторов


.
Учитывая и
исходное неравенство  , получаем равенство
, получаем равенство
 , что говорит о коллинеарности векторов.
, что говорит о коллинеарности векторов.
Тогда 


 ,.
,.
Ответ:  , где
, где  .
.
Пример 1.13
Решить систему неравенств
.
Решение.
Рассмотрим первое уравнение системы.
Введем два вектора  и
и  .
.
Вычислим разность этих векторов
 .
.
Найдем значения длин этих векторов


.
Учитывая и
исходное неравенство , получаем равенство
 , что говорит о коллинеарности векторов и о пропорциональности их координат
, что говорит о коллинеарности векторов и о пропорциональности их координат
 .
.
Рассмотрим второе уравнение системы.
Введем два вектора  и
и  .
.
Вычислим сумму этих векторов
.
Найдем значения длин этих векторов


.
Учитывая и
исходное неравенство , получаем равенство
, что говорит о коллинеарности векторов и о пропорциональности их координат
 .
.
Осталось решить систему уравнений
.
Ответ:  .
.
Пример 1.14
Доказать, что для любых чисел a, b, c, d справедливо неравенство
.
Доказательство.
Рассмотрим векторы с координатами  и
и  .
.
Вычислим сумму этих векторов
 .
.
Найдем значения длин этих векторов


 .
.
Согласно неравенству треугольника  , подставим имеющиеся значения и получим
, подставим имеющиеся значения и получим
, что требовалось доказать.
Равенство достигается в случае коллинеарности векторов.
Подводя итоги, можно определить общую схему решения задач каждого вида:
перевод содержания задачи (утверждения) на язык векторов, а именно введение обозначений векторов, координаты которых содержатся в условии задачи;
выполнение операций над векторами: вычисление суммы, разности, длин всех полученных векторов, скалярного произведения;
составление векторного равенства/неравенства (системы равенств/неравенств) или уравнения (уравнений).
упрощение векторных равенств и замена их алгебраическими уравнениями (или системой уравнений) с последующим решением;
объяснение алгебраического смысла полученного результата.
Таким образом, алгебраические задачи относятся к метрическим, и их решение алгоритмично.







 ,
,  и
и  лежат на одной прямой.
лежат на одной прямой.
 , получим
, получим ,
,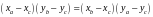 .
.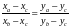
 ,
,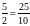 ,
, .
. и
и  ?
? .
.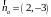 и
и 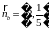 .
.
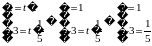 .
.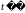 , для которого верно равенство
, для которого верно равенство 

















