Векторы на плоскости

Учитель математики

Берсенева Т.А.

№ 1«Понятие вектора. Равенство векторов».

# 1)Какова разница между векторными и скалярными величинами?

Скалярные величины определяются заданием своих числовых величин, то есть не имеют направление в пространстве.

Векторные величины или векторы характеризуются не только своим числовым значением, но и направлением в пространстве.

#2) Что такое вектор и как его обозначают?

А

В

А

В

А

В

Рис.1

# 3)Какие векторы называются коллинеарными? Приведите пример сонаправленных и противоположных направленных векторов.

Рис.3

Рис.2

#4) Какие векторы называются равными?

Рис.4

#5) Какая связь между равенством векторов и параллельным переносом?

Теорема . Равные векторы можно совместить параллельным переносом, и ,обратно, если векторы совмещаются параллельным переносом, то эти векторы равны.

A

B

C

D

Рис.5.

#6) Что такое (модуль) длина вектора?

# 7)Что вы знаете о нулевом векторе?

«№2.Сложение и вычитание векторов».

# 1)Сформулируйте правило треугольника и правило параллелограмма сложения векторов.

B

C

B

C

A

A

D

Рис. 7 .

Рис. 6 .

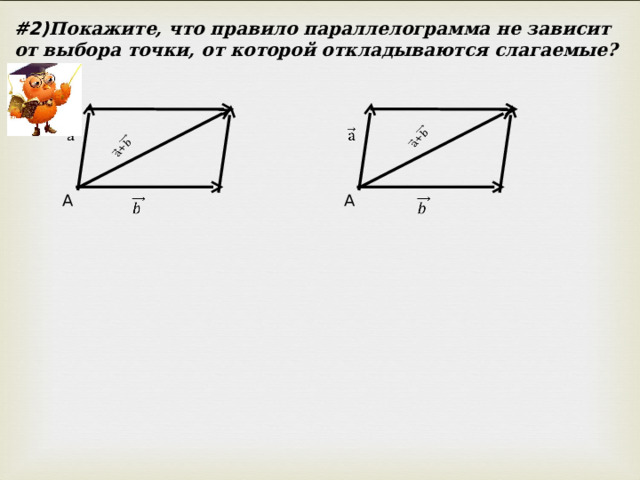
#2) Покажите, что правило параллелограмма не зависит от выбора точки, от которой откладываются слагаемые?

A

A

#3) Какими свойствами обладает сумма векторов?

1) Сложение векторов подчиняется закону ассоциативности, т.е. верно равенство.

2) Существует нулевой элемент относительно сложения векторов.

3) Для любого вектора существует противоположный ему вектор.

4) Сложение векторов подчиняется закону коммуникативности.

Последнее свойство следует из правила параллелограмма сложения векторов.

# 4)Как определяется разность векторов?

# 5)Какие векторы называются противоположными?

B

A

Рис.9.

Рис.8.

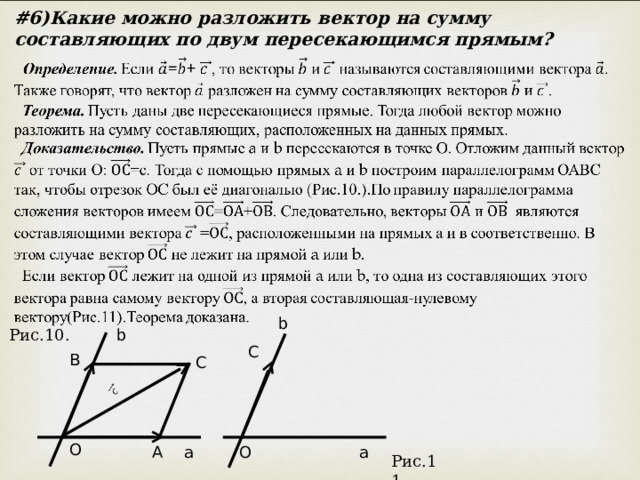
# 6)Какие можно разложить вектор на сумму составляющих по двум пересекающимся прямым?

b

Рис.10.

b

C

B

C

O

a

O

A

a

Рис.11.

«№ 3 .Умножение вектора на число и его свойства».

# 2)Как умножить ненулевое число на ненулевой вектор?

# 3)Какими свойствами обладает умножение числа на вектор?

# 4)Докажите признаки коллинеарности векторов.

# 5)Какое условие является необходимым и достаточно для того, чтобы точки A,B и C лежали на одной прямой?

«№4.Угол между векторами. Скалярное произведение векторов».

A

B

B 1

A 1

O

O 1

O

O 2

Рис.12

Рис.13

4

# 3)Что называется скалярным произведением двух векторов? Скалярное произведение векторов является числом или вектором?

Результат скалярного произведения векторов является числом (в отличие от результата рассмотренных ранее действий с векторами — сложения, вычитания и умножения на число. В таких случаях результатом был вектор). При умножении вектора на вектор получается число, так как длины векторов — это числа, косинус угла — число, соответственно, их произведение также будет являться числом.

# 4)Сформулируйте свойства скалярного произведения.

# 5)Какое условие является необходимым и достаточным для перпендикулярности двух векторов?

«№5.Координаты вектора».

# 1)Сформулируйте и докажите теорему о разложении вектора по двум неколлинеарным векторам.

C

A 1

A

O

B

B 1

Рис.14.

4

# 2)Какие векторы называются базисными векторами на плоскости?

Из теоремы о разложении вектора по двум неколлинеарным векторам вытекает, что любой вектор можно разложить по двум произвольным неколлинеарным векторам. Если на плоскости выбраны такие два неколлинеарных вектора, то они называются базисными векторами на плоскости .

# 3)Что такое координаты вектора и как их обозначают?

# 4)Напишите координаты координатных векторов.

Координаты нулевого вектора равны нулю. Координаты равных векторов соответственно равны. Координаты вектора суммы двух векторов равны сумме соответствующих координат этих векторов. Координаты вектора разности двух векторов равны разностям соответствующих координат этих векторов. Координаты вектора произведения данного вектора на число равны произведениям соответствующих координат этого вектора на данное число.

# 5)Какие свойства координат векторов вы знаете? Докажите их.

# 6)Какой вектор называется радиус-вектором точки А?

# 7)Как определяются координаты вектора, если заданы координаты его концов?

#8 )По какой формуле определяется модуль вектора?

«№6.Выражения скалярного произведения через координаты векторов».

# 1)Как можно определить скалярное произведение векторов по их координатам? Запиши соответствующие формулы и докажите их.

#2) Напишите условие перпендикулярности векторов и докажите его.

# 3)По какой формуле определяется угол между векторами? Докажите её.

Угол между векторами определяется по формулам:

«№7.Различные способы задания прямой в прямоугольной системе координат».

# 1)Какой вектор называется направляющим вектором прямой?

Определение:

Направляющий вектор прямой - это любой ненулевой вектор, лежащий на данной прямой или на параллельной ей прямой.

# 2)Какая точка называется начальной точкой прямой? Напишите уравнения прямой по точке и направляющему вектору. Каков смысл ограничения о том, что направляющий вектор не должен быть параллелям осям координат.

Начальной точкой прямой называется заданная точка.

Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).

Уравнение искомой прямой будем искать в виде: A x + B y + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям:

1×A + (-1)×B = 0, т.е. А = В.

Тогда уравнение прямой имеет вид: A x + A y + C = 0, или x + y + C/A = 0.

при х = 1, у = 2 получаем С/A = -3, т.е. искомое уравнение:

х + у - 3 = 0

# 3)Напишите уравнения прямой, проходящей через две заданные точки: С(2;5) и D(5;2) .

Решение: Уравнение прямой которая проходит через две точки:

(x-x1)/(x2-x1)=(y-y1)/(y2-y1)

Подставляем координаты точек:

(x-2)/(5-2)=(y-5)/(2-5)

(x-2)/3=(y-5)/(-3)

x-2=-(y-5)

x-2=-y+5

x+y-7=0

Ответ: x+y-7=0

# 4)Что такое нормали прямой? Напишите уравнения прямой по точке и вектору нормали.

#5) Напишите по общему уравнения прямой направляющий вектор, вектор нормали и угловой коэффициент этой прямой.

#6) По какой формуле определяется угол между прямыми?

По формуле:

#7) Как определяется расстояние от точки до прямой?

Определение.

Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.

Если задано уравнение прямой A x + B y + C = 0, то расстояние от точки M(M x , M y ) до прямой можно найти, используя следующую формулу: