Вероятностный подход к определению количества информации

Равновероятные события

Количество информации, заключенное в сообщении, определяется объемом знаний, который несет это сообщение человеку. Этот подход субъективный (зависит от конкретного человека). Разные люди, получившие одно и то же сообщение, по-разному оценивают количество информации, содержащееся в нем. Это происходит от того, что знания людей о событиях, о которых идет речь в сообщении, различны.

Пример

Первоклассник изучает таблицу умножения. Учитель сообщает

ему, что 2 х 2 = 4. Первоклассник этого раньше не знал, поэтому такое

сообщение содержит для него информацию. А для ученика 5 класса таблица умножения хорошо

известна, поэтому из такого сообщения информацию

он не получит.

На экзамен приготовлено 20 билетов.

• Чему равно количество событий, которые могут произойти при вытягивании билета?
• Равновероятны эти события или нет?
• Чему равна неопределенность знаний ученика перед тем как он вытянет билет?
• Во сколько раз уменьшится неопределенность знания после того как ученик билет вытянул?
• Зависит ли этот показатель от номера вытянутого билета?

Вернемся к примеру с монетой. Предположим, что у монеты обе стороны «орел».

• Существует ли неопределенность знаний перед броском в этом случае? Почему?
• Получите вы новую информацию после броска?
• Будет ли информативным сообщение о результате броска?
• Чему равно количество информации в этом случае?

Информация при данном подходе рассматривается как знание для человека.

За единицу измерения информации принимается уменьшение неопределенности знаний человека в 2 раза.

Эта единица называется битом и является минимальной единицей информации.

Игра «Угадай число»

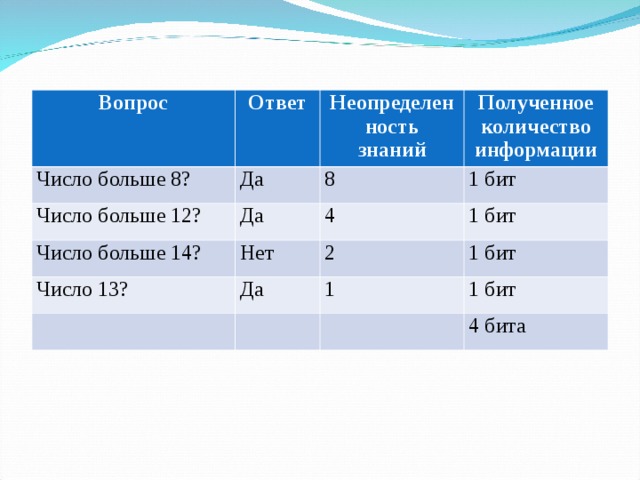
Вопрос

Число больше 8?

Ответ

Неопределенность

знаний

Да

Число больше 12?

Число больше 14?

Полученное количество информации

8

Да

Число 13?

Нет

4

1 бит

1 бит

2

Да

1 бит

1

1 бит

4 бита

Существует формула, которая связывает между собой количество возможных событий и количество информации.

N = 2 I ,где

N — количество возможных вариантов,

I — количество информации.

Если из этой формулы выразить количество информации, то получится I = log 2 N.

Неравновероятные события

В жизни же мы сталкиваемся не только с равновероятными событиями, но и событиями, которые имеют разную вероятность реализации.

Например:

1. Когда сообщают прогноз погоды, то сведения о том, что будет дождь, более вероятно летом, а сообщение о снеге — зимой.

2. Если вы — лучший ученик в классе, то вероятность сообщения о том, что за контрольную работу вы получили 5, больше, чем вероятность получения двойки.

3 . Если в мешке лежат 2 0 белых шаров и 5 черных, то вероятность достать черный шар меньше, чем вероятность вытаскивания белого.

Как вычислить количество информации в сообщении о таком событии?

Для этого необходимо использовать следующую формулу:

I = -

I – количество информации,

- вероятность события.