Треугольники
Цель урока: Формировать знания, умения и навыки по теме «треугольники. Равенство треугольников. Виды треугольников»
Задачи урока:
-
Образовательные:
-
Развивающие:
-
расширение кругозора учащихся;
-
развивать умение видеть математические понятия в окружающем нас мире;
-
развивать устную и письменную математическую речь.
-
Воспитательные:
План урока:
-
Организационный момент.
-
Сообщение темы и целей урока.
-
Изучение нового материала.
-
Применение полученных знаний при закреплении и углублении знаний по теме.
-
Подведение итогов урока, оценка знаний.
-
Работа над ошибками.
-
Домашнее задание.
Ход урока
-
Организационный момент
-
Сообщение темы и целей урока
Определение темы урока через разгадывание кроссворда, используя ранее изученный материал.
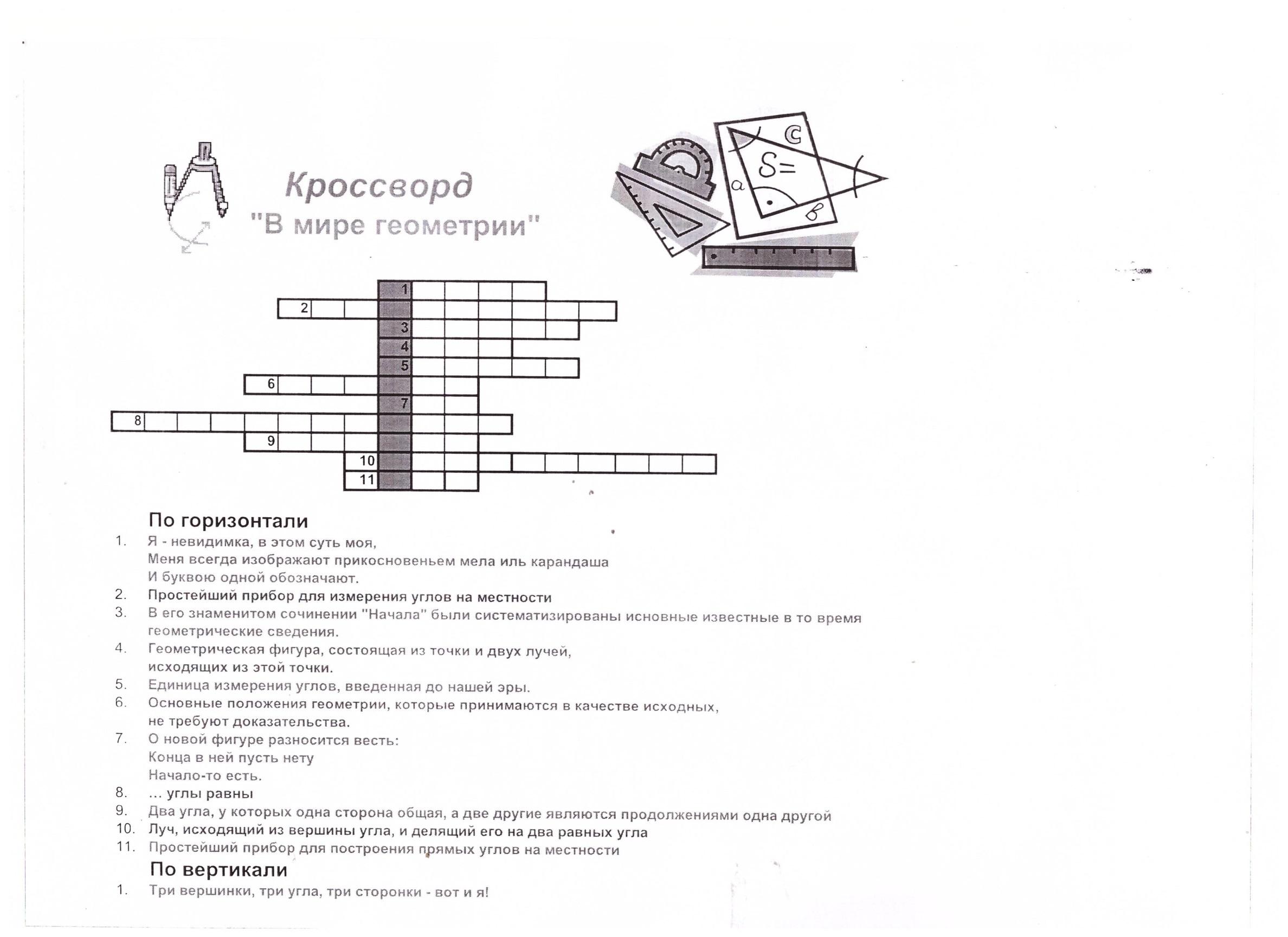
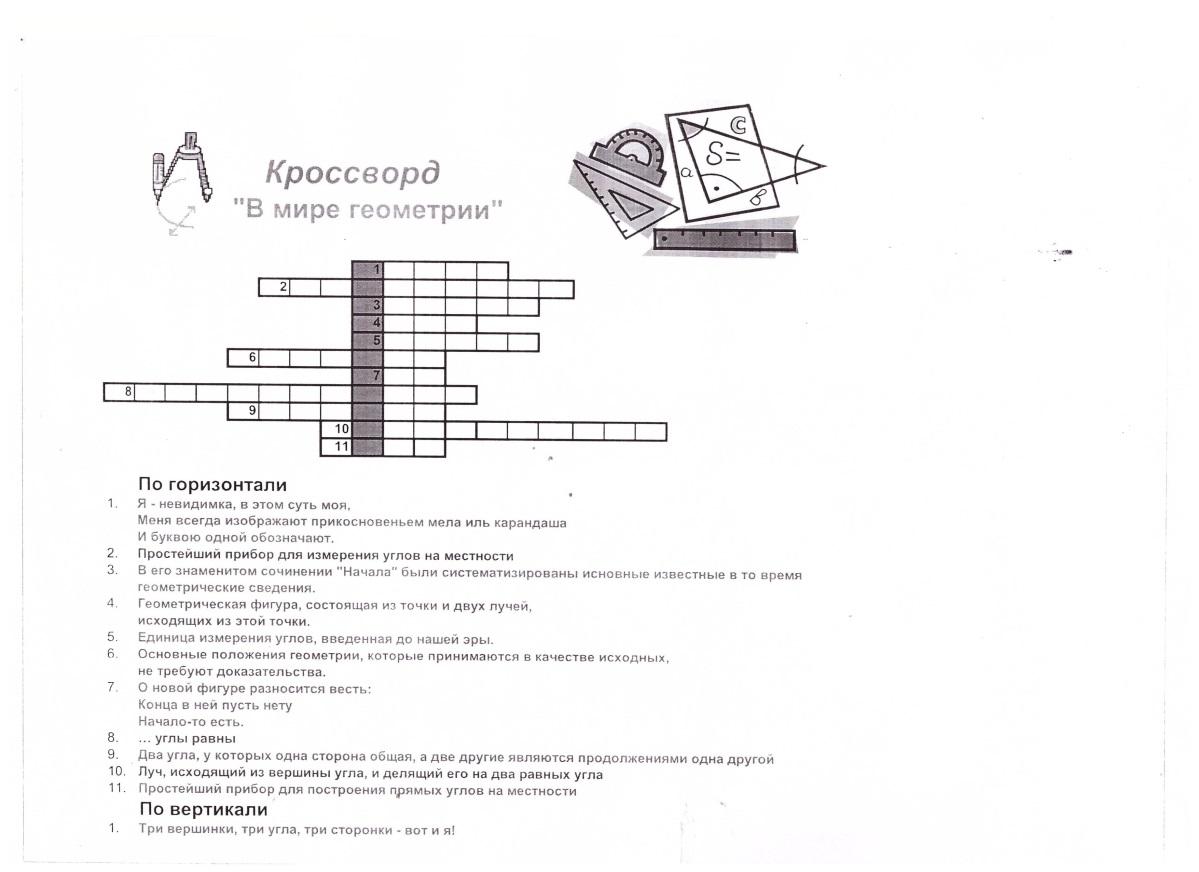
Определение задач урока:
-
узнать какая геометрическая фигура называется треугольником;
-
элементы треугольника;
-
какие бывают треугольники;
-
научиться решать задачи и правильно их оформлять;
-
развивать математическую речь
Таким образом, изучив эту тему
Вы должны знать: определение треугольника и его элементов, определение равных треугольников, что такое периметр.
Вы должны уметь: решать задачи на нахождение периметра треугольника по записи равных треугольников находить пары равных элементов этих треугольников.
-
Изучение нового материала поисково-исследовательский этап урока
Замечательный русский ученый-геометр Иван Федорович Шарыгин сказал: ”Высшее проявление духа – это разум. Высшее проявление разума – это геометрия. Клетка геометрии – треугольник. Он так же неисчерпаем, как и вселенная”. И наш первый урок главы 2 посвящен этой геометрической фигуре. А по-скольку,
«Лучший способ изучить что-либо – это открыть самому»
Д. Пойа,
то давайте проведем сегодня с вами маленькое исследование. Согласно теме урока
объектом исследования становится: ТРЕУГОЛЬНИК.
Предметом исследования:
Цель исследования: расширить представления о треугольниках и их видах.
Задачи исследования:
-
Изучение исторических сведений о треугольниках;
-
Изучение сведений о нахождении треугольников в окружающем мире;
-
Исследование свойств треугольников и их применения их в практической жизни.
Новизна исследования: актуализация изучения треугольников, как одних из интереснейших геометрических фигур в разряде многоугольников.
Знает даже и дошкольник, что такое треугольник.
Так как понятие «треугольник» уже знакомо учащимся, то целесообразно организовать изучение нового материала в виде поисковой работы.
Попробуйте сформулировать определение треугольника.
Ученики высказывают разные предложения, и учитель быстро изображает на доске высказанное предположение:
1) Из трёх прямых:
Вывод: цели не достигли, треугольник не построили.
2) Из трёх отрезков:
Вывод: цели не достигли, треугольник не построили
3) Из трёх углов:
Вывод: цели не достигли, треугольник не построили.
4) из трех отрезков и трех точек
Учитель: Какие условия должны выполняться для того, чтобы можно было построить треугольник?
Учащиеся сами предлагают условия для расположения точек и отрезков (три точки не должны лежать на одной прямой и отрезки попарно соединяют эти точки).
И доходят до предположения: из трёх точек и трёх отрезков, не лежащих на одной прямой, соединяющих эти точки.
Попробуйте сформулировать определение треугольника, сделав его чертеж.
Ученики: треугольник это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой и трёх отрезков, попарно соединяющих эти точки.
-
указывает, что отрезки называются в треугольнике сторонами, а точки вершинами;
-
дает задание учащимся записать в тетради данное определение, построить произвольный треугольник, записать его вершины, стороны, углы
-
Исследовательская деятельность (работа в группах)
Первая группа «Жесткость треугольника»
Нам надо было доказать, что треугольник жесткая фигура. Жесткая фигура — это фигура, не подверженная деформации.
И действительно:
Вырезанные из картона 4 полоски мы попробовали соединить между собой булавками или декоративными кнопками в четырехугольник, а затем попробовали изменить форму четырехугольника (просто взявшись руками за две противоположные стороны и покачать вверх-вниз). Получаем, что можно изменять градусную меру углов четырехугольника, не меняя длины его сторон. Можно менять величины углов у пятиугольников, шестиугольников и многоугольников с большим количеством сторон.
С треугольником так поступить не удалось. Из 3-х полосок сложим треугольник и соединим кнопками или булавками и попробуем изменить форму треугольника.
Стороны треугольника определяют его углы однозначно.
Треугольник не подвержен деформации. В нём нельзя сдвинуть или раздвинуть никакие две стороны, т. е. нельзя изменить ни один угол. Действительно, если бы это удалось, то мы получили бы новый треугольник, не равный исходному.
Поэтому треугольник — жесткая фигура. Из всех многоугольников только треугольник является жесткой фигурой.
Вывод: Треугольник — фигура жёсткая. Если заданы три его стороны, то форма треугольника уже не может измениться.
?? Что в жизни вы встречали в форме треугольника?
Ответ: крыши домов; подставка для подтягивания; музыкальные инструменты; сыр; украшения; линейка; дорожный знак; окна и т.п.
Вторая группа «Равные треугольники и их свойства»
Нам надо было доказать, что среди треугольников встречаются равные.
Мы воспользовались определением равных отрезков (два отрезка равны, если их можно совместить наложением). И совмещали все предложенные нам треугольники. И, действительно, среди предложенных треугольников такие нашлись. Значит, треугольники называются равными, если их можно совместить наложением.
Наша группа пришла к выводу, что против равных сторон лежат равные углы, а против равных углов – равные стороны.
Вывод:
Определение. Треугольники называются равными, если их можно совместить наложением.
Свойства равных треугольников. Против равных сторон лежат равные углы, а против равных углов – равные стороны
Третья группа «Классификация (виды) треугольников»
Нам надо было распределить по группам предложенные треугольники.
Мы заметили, что треугольники различаются углами и длиной сторон.
Например, были предложены треугольники, у которых все углы острые, у которых есть по одному прямому и тупому углу.
С другой стороны, у треугольников были стороны с равными и разными длинами.
Результаты наших исследований мы занесли в таблицу:
| по сторонам по углам | равносторонние | равнобедренные | разносторонние |
| остроугольные | 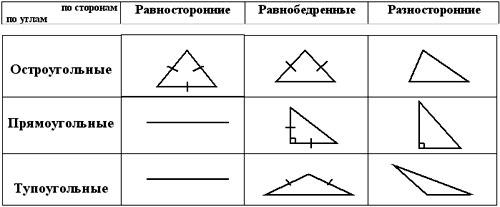
| 
| 
|
| прямоугольные |
| 
| 
|
| тупоугольные |
| 
| 
|
Вывод:
Определения.
Треугольник, у которого все стороны равны, называется равносторонним.
Треугольник, у которого две стороны равны, называется равнобедренным.
Треугольник, у которого все углы острые, называется остроугольным.
Треугольник, у которого есть прямой угол, называется прямоугольным.
Треугольник, у которого есть тупой угол, называется тупоугольным.
Периметр треугольника – сумма длин его сторон.
-
Рефлексия работы в группах
И, так, давайте подведем итоги нашей исследовательской деятельности.
Что называется треугольником?
Тест 1 (с.52)




 Знает даже и дошкольник,
Знает даже и дошкольник,
Что такое треугольник.
А уж вам-то как не знать!
Но совсем другое дело –
Быстро, точно и умело
Треугольники считать.
Например, в фигуре этой
Сколько разных? Рассмотри!
Все внимательно исследуй
И по краю, и внутри
Сколько всего треугольников можно назвать на рисунке?
1 группа. «Жесткость».
Это свойство треугольника используется, в частности, при создании железных ажурных конструкций. Мосты, башни, подъемные краны, каркасы зданий, опоры для высоковольтных линий электропередач изготавливают таким образом, чтобы они содержали как можно больше треугольных элементов.
2 группа. Равные треугольники и их свойства»
Тест 2 (с.53)
Какие треугольники, по-вашему, мнению можно совместить наложением?

3 группа. «Классификация треугольников»
Тест 3 (с.54)

-
Применение полученных знаний при закреплении и углублении знаний по теме
№ 53.


Пусть в равнобедренном Δ АВС АВ = ВС = 14 дм, АС = 8 дм, то
РАВС = 2 · 14 + 8 = 36 (дм), но
РАВС = Р DEF, то каждая сторона
равностороннего Δ DEF
Р DEF = 36 : 3 = 12 (дм)
Ответ: 12 дм.
-
Рефлексия
Простая это фигура треугольник: три вершины, три стороны, три угла. А задумаешься…, нет, вовсе не простая, мы ещё многое о ней не знаем. Не умеем вычислять площади треугольников, не знаем о признаках равенства и подобии треугольников, о признаках равенства прямоугольных треугольников, не знаем и не умеем применять теоремы косинусов, синусов, и многое ещё осталось загадочным для вас.
-
Подведение итогов урока, оценка знаний
Оцените свою работу в группе, заполнив таблицу
-
Постановка домашнего задания
§ 1, гл.2, №№ 51, 55
Подготовить сообщения по темам:
-
Место треугольника в истории.
-
Треугольник и его роль в жизни народов.
-
Треугольник в строительстве.
-
Треугольник и творчество
-
Работа над ошибками
Математический диктант (с последующей проверкой)
Отметьте знаком «+»правильные утверждения и знаком « – » – ошибочные.
Треугольник является объемной фигурой.
Треугольник является плоской фигурой.
Треугольником называется геометрическая фигура, состоящая из трех точек, соединенных попарно отрезками.
Треугольником называется геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой и соединенных попарно отрезками.
В треугольнике АВС стороны, прилежащие к углу ВАС – это АВ и АС.
Периметром треугольника называется сумма длин всех сторон этого треугольника.
Если два треугольника равны, то их соответственные элементы могут быть не равны.
Если два треугольника равны, то их периметры всегда равны.
В равных треугольниках против соответственно равных сторон лежат равные углы.
В равных треугольниках АВС и МKD соответственными являются элементы: АС и МD, ВС и КD, АВ и МК;  А и
А и 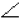 М,
М, 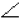 В и
В и 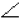 К,
К, 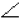 С и
С и 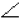 D.
D.
правильный ответ – +–+++–+++
Решение задач
Ребята находят решение в группах, помогая друг другу. Результаты обсуждаются в классе.
№1
Известно, что треугольник МРК равен треугольнику СОЕ. Запишите равные углы и стороны этих треугольников:
№2
Даны два равных ∆DBE и ∆KOP, DE=4,5см, DВ=9см, 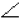 D=60º,
D=60º, 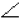 B=30º. Найдите соответствующие стороны и углы KOP.
B=30º. Найдите соответствующие стороны и углы KOP.
№3
На столах лежат треугольники разного цвета. Обозначьте вершины. Найдите периметр треугольника и результат напишите с обратной стороны.














 Знает даже и дошкольник,
Знает даже и дошкольник, 






















