Программа внеурочной деятельности по математике
для учащихся 9 класса
«Применение уравнений в повседневной жизни»
Составитель: учитель математики ǀ
квалификационной категории
Гильфанова Алсу Махияновна.
2019-2020 уч. год
Пояснительная записка Современные дети растут в условиях интенсивно формирующейся рыночной экономики страны. Для них необходимыми стали знания таких областей наук, как экономика, управление, потому что профессии, которые они получают на основе этих знании, будут не только престижны, но и высокооплачиваемы. Данная внеурочная деятельность «Применение уравнений в повседневной жизни» поддерживает изучение основного курса математики и способствует лучшему усвоению базового курса математики. Данная программа курса по выбору своим содержанием сможет привлечь внимание учащихся, которым интересна математика и ее приложения, и которым хочется глубже познакомиться с ее методами и идеями. Внеурочная деятельность поможет иметь представления об уравнениях, об их роли в повседневной жизни. Во многих школьных учебниках можно встретить задачи, однако в них отсутствует компактное и четкое изложение соответствующей теории вопроса! Текстовые задачи включены в материалы итоговой аттестации за курс основной школы, в КИМ ы и ОГЭ, в конкурсные экзамены. Однако практика показывает, что задачи на тему о повседневной жизни вызывают затруднений у учащихся и очень многие окончившие школу не имеют прочных навыков обращения с задачами в повседневной жизни. Понимание темы и умение решить задачи с помощью уравнений необходимы каждому человеку: прикладное значение этой темы очень велико и затрагивает финансовую, экологическую, социологическую и другие стороны нашей жизни. Познавательный материал внеурочной деятельности будет способствовать не только выработке умений и закреплению навыков вычислений, но и формированию устойчивого интереса учащихся к процессу и содержанию деятельности, а также познавательной активности.
Внеурочная деятельность представлена в виде практикума, который позволит систематизировать и расширить знания учащихся в решении задач по математике и позволит начать целенаправленную подготовку к сдаче экзамена в форме ОГЭ и в дальнейшем ЕГЭ.
Основные цели программы
Так как, что в основе реализации программы лежит системно-деятельностный подход, основными целями являются:
- выполнить некоторые содержательные пробелы основного курса, придающие ему необходимую целостность;
- показать некоторые нестандартные приемы решения задач на основе свойств модуля;
- способствовать интеллектуальному развитию учащихся, формированию качеств мышления, характерных для математической деятельности и необходимых человеку для жизни в современном обществе, для общей социальной ориентации и решения практических проблем.
Задачи реализации программы
- научить учащихся решать задачи более высокой, по сравнению с обязательным уровнем сложности, необходимой для применения практической деятельности;
- овладеть рядом технических и интеллектуальных математических умений на уровне свободного их использования;
-привить учащимся основы экономической грамотности;
Данная внеурочная деятельность предполагает компактное и четкое изложение теории вопроса, решение типовых задач, самостоятельную работу.
Логический анализ содержания темы позволил выделить группы задач, которые и составили основу изучаемого курса. Каждой группе задач предшествует небольшая историческая и теоретическая справка. Кроме того, рассматриваются задачи с практическим содержанием, а именно такие задачи, которые связаны с применением уравнений в повседневной жизни.
Программа может быть эффективно использована в 9 -11 классах с любой степенью подготовленности, способствует развитию познавательных интересов, мышления учащихся, предоставляет возможность подготовиться к сознательному выбору профиля обучения и дальнейшей специализации.
Планируемые результаты
Реализация программы внеурочной деятельности «Применение уравнений в повседневной жизни» направлено на достижение следующих результатов:
1) в направлении личностного развития
• развитие логического и критического мышления, способности к умственному развитию;
• воспитание качеств личности, способных принимать самостоятельные решения;
• развитие интереса к математическому творчеству и математических способностей;
2) в метапредметном направлении
• формирование представлений о значимости математики в развитии современного общества;
• формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;
3) в предметном направлении
• овладение математическими знаниями и умениями, необходимыми для продолжения обучения в 10-11 классах или в других общеобразовательных учреждениях, изучения предметов, применения в повседневной жизни.
В результате изучения внеурочной деятельности учащиеся должны:
-уметь решать более сложные уравнении;
- знать широту применения уравнений в решении жизненных задач;
- производить прикидку и оценку результатов вычислений.
В силу большой практической значимости данный курс вызывает интерес, является средством обучения и средством развития интеллектуальных качеств личности учащихся.
Для учащихся, которые пока не проявляют заметной склонности к математике, эти занятия могут стать толчком в развитии интереса к предмету и вызвать желание узнать больше. Хотя при изучении курса не ставится цель выработки каких-либо специальных умений и навыков, при достаточно полном рассмотрении вопросов курса несомненно появится интерес в подготовке учащихся.
Виды деятельности на занятиях: беседа, практикум, консультация, работа с компьютером.
Предполагаемые результаты.
Изучение данного курса дает учащимся возможность:
-
повторить и систематизировать ранее изученный материал школьного курса математики;
-
освоить основные приемы решения задач;
-
познакомиться и использовать на практике нестандартные методы решения задач;
-
повысить уровень своей математической культуры, творческого развития, познавательной активности;
-
познакомиться с возможностями использования электронных средств обучения, в том числе Интернет-ресурсов, в ходе подготовки к итоговой аттестации в форме ОГЭ и в дальнейшем ЕГЭ.
Оценивание результатов деятельности обучающихся
Реализация программы внеурочной деятельности «Применение уравнений в повседневной жизни» подразумевает выполнение группового проекта, обязательно для каждого обучающегося. Учащиеся разрабатывают план и комплекс задач по одной из тем. Защищают свой проект.
Критерии оценки группового проекта:
1. Познавательные учебные действия: способность к групповому приобретению знаний и решению проблем
2. Предметных знаний и способов действий, проявляющаяся в умении раскрыть содержание работы, грамотно и обоснованно в соответствии с рассматриваемой проблемой/темой использовать имеющиеся знания и способы действий.
3. Регулятивные учебные действия проявляются в умении самостоятельно планировать и управлять своей познавательной деятельностью во времени, использовать ресурсные возможности для достижения целей.
4. Коммуникативные учебные действия, проявляются в умении ясно изложить и оформить выполненную работу, представить её результаты, учебные ответить на вопросы.
Тематическое распределение количества часов
| № | Тема, раздел | Количество часов | Творческая работа, проекты |
| 1 | Общие сведения об уравнениях | 1 | практика |
| 2 | Целые рациональные алгебраические уравнения с одной неизвестной первой степени | 1 | практика |
| 3 | Целые рациональные алгебраические уравнения с одной неизвестной второй степени | 1 | практика |
| 4 | Решение уравнении: |f (x)| = |g (x)| и  |f (x)| = g (x), равносильность уравнений |f (x)| = |g (x)| к f (x) = g (x); и f (x) = - g (x), |f (x)| = g (x), равносильность уравнений |f (x)| = |g (x)| к f (x) = g (x); и f (x) = - g (x),
 |f (x)| = g (x) к |f (x)| = g (x) к
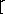 f (x) = g (x); f (x) = g (x);
f (x) = - g (x), g (x)0, g (x) | 3 | Практика Групповая работа |
| 5 | Решение уравнений содержащих знак модуля: | а | + | в | = с | 3 | Инд. работа |
| 6 | Решение рациональных уравнении: Рn(х)=хn +an-1xn-1+ … +a1x+a0 | 5 |
|
| 7 | Решение задач по химии с помощью уравнений. | 2 | Групповая работа Анализ |
| 8 | Задачи на проценты, сплавы и смеси. | 2 | Групповая работа Анализ |
| 9 | Решение задач по физике с помощью уравнений: скорость, время, расстояние. | 3 | Групповая работа Анализ |
| 10 | Решение задач по экономике с помощью уравнений. | 2 |
|
| 11 | Решение задач с литературными и историческими сюжетами. | 2 |
|
| 12 | Решение комбинированных уравнений | 3 |
|
| 13 | Задачи с параметрами | 3 |
|
| 14 | Решение задач, которые встречаются в ОГЭ (Задачи на совместную работу.) | 3 | Групповая работа Анализ |
Содержание программы.
Тема 1. Общие сведения об уравнениях. (1ч)
Цель: Повторить решение уравнений способом переноса слагаемых из одной части в другую, изменив при этом их знаки; развивать логическое мышление.
Тема 2. Целые рациональные алгебраические уравнения с одной неизвестной первой степени. (1ч)
Цель: Решение рациональных уравнений; повторить решение уравнений способом сокращения дробей, приведению дробей к наименьшему общему знаменателю; развивать логическое мышление.
Рациональные уравнения. Подбор корней. Метод неопределённых коэффициентов. Разложение на множители.
Методические рекомендации. В ходе изучения этой темы учащиеся должны усвоить основные способы решения рациональных уравнений. Решение каждой задачи, разобранной на занятиях, представляет собой метод решения большого класса задач. Эти методы повторяются и углубляются при решении последующих задач.
Тема 3. Целые рациональные алгебраические уравнения с одной неизвестной второй степени. (1ч)
Цель: Дробно-рациональные уравнения. Подбор корней. Разложение на множители. Замена переменной. Выделение полных квадратов. Однородные уравнения. Симметрические и возвратные уравнения. Обобщённая теорема Виета.
Методические рекомендации. В ходе изучения этой темы учащиеся должны усвоить основные способы решения рациональных уравнений высших степеней. В каждой лекции разбираются задачи разного уровня сложности. От простых, повторяющих школьную программу задач (таких немного), до сложных задач, решение которых обеспечивает хорошую и отличную оценку на экзаменах.
Тема 4. Решение уравнения: |f (x)| = |g (x)| и |f (x)| = g (x) (3ч)
Цель: Закрепить определение модуля и нахождение модуля выражений в ходе выполнения упражнений; воспитывать у детей любознательность желание участвовать в различных соревнованиях. Расширить интерес учащихся к изучению математики.
Метод обучение: Объяснение, практические упражнения, лекция, беседа.
Тема 5. Решение уравнений, содержащих знак модуля:
| а | + | в | = с (3ч)
Цель: Устранить пробелы в знаниях по решению основных задач по нахождению модуля:
а) нахождение модуля числа,
б) нахождение модуля выражения.
Актуализируются знания об арифметических и алгебраических приемах решения задач.
Метод обучения: лекция, беседа, объяснение, устные упражнения, письменные упражнения.
Форма контроля: проверка самостоятельно решенных уравнений.
Тема 6. Решение рациональных уравнений: Рn(х)=хn +an-1xn-1+ … +a1x+a0 (5 ч)
Ц е л ь: Дать понятие корня многочлена Рn(х), познакомить учащихся теоремой Безу, показать деление с остатком; систематизировать знания в ходе выполнения заданий.
Методы обучения: беседа, устные и письменные упражнения.
Форма занятий: комбинированные занятия.
Тема 7. Решение задач по химии с помощью уравнений. (2 ч).
(Задачи на смеси, сплавы, концентрацию.)
Ц е л ь: усвоение учащимися понятий концентрации вещества, процентного раствора. Формирование умения работать с законом сохранения массы. Обобщение полученных знаний при решении задач.
Форма занятий: комбинированные занятия.
Метод обучения: рассказ, объяснение, выполнение практических заданий.
Форма контроля: самостоятельная работа.
Тема 8. Задачи на проценты, сплавы и смеси. Решение задач с помощью таблиц. (2ч)
Тема 9. Решение задач по физике с помощью уравнений. (3ч)
(скорость, время, расстояние.)
Цель: развить интерес учащихся к изучению математики, учить применять полученные знания в разных ситуациях.
Метод обучения: беседа, решение задач.
Тема 10. Решение задач по экономике с помощью уравнений. (2ч)
Цель: Учить решать задачи экономического характера, повторить и углубить знания о способах решения задач с помощью уравнении.
Метод обучения: Объяснения, устные упражнения, письменные упражнения.
Форма контроля: проверка самостоятельно решенных задач.
Тема 11. Решение задач с литературными и историческими сюжетами. (2ч)
Цель: Вызвать интерес учащихся воспитывать желание узнать больше, развивать интеллектуальные качества личности учащихся. Сформировать умение решать задачи, повысить уровень математической культуры
Метод обучение: рассказ, объяснение, практическая работа.
Формы контроля: проверка самостоятельно решенных задач.
Тема 12. Решение комбинированных уравнений. (3ч)
Итоговое занятие предлагается провести в форме круглого стола с презентациями. Комбинированные уравнения (Учащиеся должны знать:
- этапы исследовательской деятельности.
Учащиеся должны уметь:
- использовать этапы исследовательской деятельности на практике
Методические рекомендации. Изучение этой темы предполагает систематизацию полученных знаний по теме и углубление школьного курса. Систематизируются способы решения уравнений и систем уравнений. Особое внимание уделяется преобразованиям выражений, решению уравнений, систем уравнений и комбинированным заданиям, которые предлагаются на итоговой аттестации.
Материал излагается в форме беседы с учащимися при повторении, в форме лекции при рассмотрении сложных тригонометрических уравнений. При решении уравнений используются коллективная, групповая и индивидуальная формы работы с учащимися. Качество усвоения темы проверяется выполнением самостоятельной работы в тестовой форме на последнем занятии.
Тема 13. Задачи с параметрами (3ч)
Урок № 1. Параметр: понятие, общие методы решения
Цель - определение уравнения и неравенства с параметром, области определения уравнения с параметром; общие приемы решения заданий с параметром. Учащимся раскрывается содержание понятия параметр, его интерпретация, основные теоремы.
Урок № 2. Методы решения задач с параметром.
Цель - введение различных методов решения задач с параметром. Учащимся дается характеристика каждого метода решения задач с параметром; обоснование выбора метода решения. в зависимости от условия, вопроса задачи.
Урок № 3. Линейные уравнения и неравенства, уравнения и неравенства, приводимые к линейным.
Цель - формирование навыка решения линейных уравнений и неравенств с параметром, а также уравнений и неравенств, приводимых к ним.
Тема 14. Решение уравнений, которые встречаются в ОГЭ. (3ч)
Цель - формирование навыка решения тригонометрических уравнений и, а также уравнений и неравенств, приводимых к ним, которые встречаются в ЕГЭ.
ЛИТЕРАТУРА ДЛЯ УЧИТЕЛЯ 1. Башарин Г. П. Начала финансовой математики. - М., 1997.
2. Виленкин Н. Я. За страницами учебника математики. - М.: Просвешещение, 1989.
3.Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И. Математика 6. - М.: Дрофа, 2000.
4. Водинча М. И., Лайкова Г. А., Рябова Ю. К. Решение задач
на смеси, растворы и сплавы методом уравнений. Математика в школе. 2001. №4.
5.Денишева Л. О., Бойченко Е. М., Глазков Ю. А. и др. Готовимся К единому государственному экзамену. Математика. - М.: Дрофа, 2003.
6. Никольский С. Н., Потапов М. К., Решетников Н. Н. Алгебра в 7 классе: методические материалы. - М: Просвещение, 2002.
7. Сканави М.И. Решение конкурсных задач по математике. М.: Инфолайн.
ЛИТЕРАТУРА ДЛЯ УЧЕНИКА 1. Водинча М. И., Лайкова Г. А., Рябова Ю. К. Решение задач
на смеси, растворы и сплавы методом уравнений. Математика в школе. 2001. №4.
2. Звавич Л.И., Шляпочнин Л.Я., Козулин В.В. Контрольные и проверочные работы по алгебре. 9 класс. - М.: Дрофа, 2001.
3.Макарычев Ю.Н., Миндюк Н.Г. Алгебра 9.-М.: Просвещение, 2001.
4.Никольский С.М., Потапов М.К. Алгебра и начала анализа 10.- М. - Порсвещение, 2015.
5. Сканави М.И. Решение конкурсных задач по математике. М.: Инфолайн.
Интернет-источники:Открытый банк задач ЕГЭ: http://mathege.ru
Он-лайн тесты: http://uztest.ru/exam?idexam=25
http://egeru.ru
http://reshuege.
Приложение 1
Тема 4. Решение уравнения: |f (x)| = |g (x)| и |f (x)| = g (x) (3ч)
1.│2х-3│=3-2х Ответ: (- ∞;1,5]
2.│3х-5│=5-3х Ответ: (- ∞;1 ]
]
3.│4-5х│=5х-4 Ответ: [0,8; ∞)
4.│7-4х│=7-4х Ответ: (- ∞; 1,75]
5.│х-1999│=2000 Ответ: 3999; -1
6.│3х-1│=4-2х Ответ: - 3; 1
7.│5 - 3х│=2х +1 Ответ: 0,8; 6
8.│5х +2│=3-3х Ответ: -2,5; 0,125
9.│х+2│=2(3-х) Ответ: 1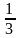
10. 3│х│=х 2-10 Ответ: - 5; 5
11. х 2 - 4x - 4=2│х-2│ Ответ: -2; 6
Приложение 2
Тема 5. Решение уравнений содержащих знак модуля:
| а | + | в | = |а + в| (3ч)
1. │ x-1999│+│1999-x│=2000 Ответ: 2999; 999 2. │ x+3│+│2x -1│=8 Ответ: -3
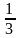
; 2 3. │ x-3│+2│x +1│= 4 Ответ: -1 4. │ 4 - x│+│x - 2│= 4 Ответ: [2; 4) 5. │ 2x + 7│-2│3x-1│= 4x+1 Ответ: -1; 1 6. │ x-3│+│x + 5│= 8 Ответ: [-5; 3] 7. │5x-13│-│6-5x│= 7 Ответ: (-∞; 1,2] 8. │3x- 8│-│3x -2│= 6 Ответ: (-∞;

] 9. │16-9x│-│9x -5│= 11 Ответ: (-∞;

] 10. │7x-12│-│7x-1│=1 Ответ:

Приложение 3
Тема 6. Решение рациональных уравнений:
Рn(х)=хn +an-1xn-1+ … +a1x+a0 (5часа)
1. х3 - 8х2 – х + 8 = 0 Ответ: - 1; 1; 8
2. х3 - 5х2 + 8х - 4 = 0 Ответ: 1; 2
3. 27х3 + 9х2 – 48х + 20 = 0 Ответ:  ; - 1
; - 1
4. у3 + 3у2 – 20у + 100 = 0 Ответ: - 5
5. х4 - 20х2 + 64 = 0 Ответ: - 4; - 2; 2; 4
6. При каких значениях к уравнение х4 - 13х2 + к = 0 имеет четыре корня?
Ответ: к € (0; 42,25)
7. (х – 1) 5 + (х + 3) 5 = 242(х +1) Ответ: -2; -1; 0
Приложение 4
Тема 7. Решение задач по химии с помощью уравнений. (2 ч)
(Задачи на смеси, сплавы, концентрацию.)
Задача 1. Из 40 тонн железной руды выплавляют 20 тонн стали, которая содержит 6 % примесей. Каков процент примесей в руде?
Задача 2. Сплав меди и алюминия массой 10 кг содержит 35% меди. Сколько килограммов в этом сплаве составляет алюминий?
Задача 3. Два сплава с массами м1 и м2 кг содержат медь и серебро в отношениях 12: 1 и 16:3 соответственно. Эти два сплава сплавили с м3 кг чистого серебра и м4 кг чистой меди. Определите процент серебра в образовавшемся сплаве.
Задача 4. Морская вода содержит 0,05 часть соли (по весу). Сколько килограммов пресной воды нужно прибавить к 40 кг морской воды, чтобы содержание соли в смеси составляло 0,02 часть воды?
Задача 5. Имеется два куска сплава олова и свинца, где олово содержит 0,6 и 0,4 части кусков. По сколько граммов от каждого куска надо взять, чтобы получить 600 г сплава, где олово составляет 9/20 часть сплава? (Ответ: 150 г; 450 г.)
Задача 6. Кусок сплава меди и цинка массой 36 кг содержит 0,45 часть которой содержит медь. Сколько килограммов меди нужно добавить к этому куску, чтобы полученный новый сплав содержал 0,6 часть меди от общего количества.? (Ответ: 13,5 кг.)
Задача 7. Одном слитке 0,35 часть серебро, а другом 0,65 часть серебро. Сплавляют и получают слиток массой 30 г, 0,47 часть которого серебро. Какова масса каждого из этих слитков? (Ответ: 12 г; 18 г)
Задача 8. В 500 кг руды содержится некоторое количество железа.
После удаления из руды 200 кг примесей, содержащих в среднем 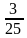 железа, содержание железа в оставшейся руде повысилось на 20%. Определите, какое количество железа осталось еще в руде? (Ответ: 187,5 кг)
железа, содержание железа в оставшейся руде повысилось на 20%. Определите, какое количество железа осталось еще в руде? (Ответ: 187,5 кг)
Приложение 5
Тема 8. Задачи на проценты, сплавы и смеси.
Задача 1. Смешав 60%−ый и 30%−ыйрастворы кислоты и добавив 5 кг чистой воды, получили 20%−ый раствор кислоты. Если бы вместо 5 кг воды добавили 5 кг 90%−го раствора той же кислоты, то получили бы 70%−ый раствор кислоты. Сколько килограммов 60%−го раствора использовали для получения смеси?
| раствор | масса, кг | %кислоты | масса кислоты |
| 1 | х | 60% | 0,6х |
| 2 | у | 30% | 0,3у |
| 3 | х+у+5 | 20% | 0,2(х+у+5) |
| раствор | масса, кг | %кислоты | масса кислоты |
| 1 | х | 60% | 0,6х |
| 2 | у | 30% | 0,3у |
| 3 | х+у+5 | 90% 70% | 5 0,9=4,5 (х+у+5) 0,9=4,5 (х+у+5) 0,7 0,7 |

Ответ: 2
Задача 2. Имеется два сплава с разным содержанием меди: в первом содержится 60%, а во втором — 45% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 55% меди?
| раствор | масса, кг | %кислоты | масса кислоты |
| 1 | х | 60% | 0,6х |
| 2 | у | 45% | 0,45у |
| 3 | х+у | 55% | 0,55 (х+у) (х+у) |
0,6х+0,45у=0,55(х+у)
х=2у
 Ответ:
Ответ: 
Задача № 3. Свежие фрукты содержат 80% воды, а высушенные — 28%. Сколько сухих фруктов получится из 288 кг свежих фруктов?
|
| масса, кг | % воды свежих фруктов | % воды высушенных фруктов | масса мякоти, кг |
| свежие фрукты | 288 | 80% | 100 –80=20% | 288 0,2 0,2 |
| высушенные фрукты | х | 28% | 100 –28=72% | х 0,72 0,72 |
х  0,72=288
0,72=288 0,2
0,2
х =80 Ответ: 80
Задача № 4. На пост главы администрации города претендовало три кандидата: Журавлёв, Зайцев, Иванов. Вовремя выборов за Иванова было отдано в 2 раза больше голосов, чем за Журавлёва, а за Зайцева — в 3 раза больше, чем за Журавлёва и Иванова вместе. Сколько процентов голосов было отдано за победителя? Ответ: 75%
Задача № 5. Первый сплав содержит 5% меди, второй — 13% меди. Масса второго сплава больше массы первого на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава.
Ответ: 16
Задача № 6. Свежие фрукты содержат 86 % воды, а высушенные — 23 %. Сколько требуется свежих фруктов для приготовления 72 кг высушенных фруктов? Ответ: 396
Приложение 6
Тема 9. Решение задач по физике с помощью уравнений. (3ч)
Задача. 1. Длина окружности переднего колеса кареты равна 3м, а заднего – 4,5м. Какое расстояние проехала карета, если переднее колесо сделала на 20 оборотов больше заднего? Ответ: 180м.
Задача 2. В реку впадает приток. Катер отходит от пристани А на притоке, идет вниз по течению 80 км до реки, далее по реке вверх против течения до пристани В, затратив 18 ч на весь путь от А до В. Затем катер возвращается обратно. Время обратного движения от В до А по тому же пути равно 15 ч. Собственная скорость катера, т. е. скорость катера в стоячей воде равна 18 км/ч, скорость течения реки равна 3 км/ч. Каково расстояние от пристани А до пристани В и какова скорость течения притока? (Ответ:2 км/ч;290 км.)
Задача 3. В озеро впадают две реки. Лодка отплывает от пристани А на первой реке, плывет 36 км вниз по течению до озера, далее 19 км по озеру (в озере нет течения) и 24 км по второй реке против течения до пристани В. На весь путь от А до В лодка затрачивает 8 ч. Из них 2 ч плывет по озеру. Скорость течения первой реки на 1 км/ч больше, чем скорость течения второй реки. Найдите скорость течения каждой реки. (Собственная скорость лодки постоянна) (Ответ:2,5 км/ч и 1,5 км/ч).
Задача 4. На расстояние 100 км грузовой автомобиль расходует не менее, чем на 10 л бензина больше, чем легковой. Расходуя 1 л бензина, грузовой автомобиль проходит на 5 км меньше, чем легковой. Какое расстояние может преодолеть легковой автомобиль, расходуя 1 л бензина? (Ответ: больше 5 км, но не более 10 км.)
Задача 5. 3 мотоцикла стартуют одновременно из одной точки кольцевого шоссе в одном направлении. I мотоциклист впервые догнал II, сделав 4,5 круга после старта, а за 0,5 ч до этого он впервые догнал третьего мотоциклиста. II мотоциклист впервые догнал III через 3 ч после старта. Сколько кругов в час делает первый мотоциклист? (Ответ: 3 круга/ч)
Приложение 7
Тема 10. Решение задач по экономике с помощью уравнений. (2ч)
Задача 1. Цена билета для входа на стадион была 180 р. После снижения входной платы число зрителей увеличилось на половину, а выручка выросла на 0,25. Сколько стоил билет после снижения входной платы?
Задача 2. Два печника могут сложить печь за 12 ч. Если первый печник будет работать 2 ч, а второй 3 ч, то они выполнят только 20% всей работы. За сколько часов может сложить печь каждый печник, работая отдельно?
Ответ: 20ч, 30ч.
Задача 3. Две копировальные машины, работая одновременно, сделали копию пакета документов за 20 мин. За какое время каждая из них может выполнить эту работу. Если известно. Что первой машине требуется для этого на 30 мин меньше, чем второй?
Ответ: 30 мин, 60 мин.
Задача 4. Бригада должна была изготовить определенное количество стульев за 10 дней. Однако она изготовила в день на 20 стульев больше, чем планировала, поэтому за 5дня до срока ей осталось изготовить 58 стульев. Сколько стульев должна была изготовить бригада?
Ответ: 660 стульев.
Задача 5. Торговец продает орехи двух сортов: одни по 90 центов, другие по 60 центов за килограмм. Он хочет получить 50 кг смеси по 72 цента за килограмм. Сколько для этого потребуется орехов каждого сорта?
Ответ: 20 кг и 30 кг.
Задача 6. Одна из труб может наполнить водой бак на 10 мин быстрее другой. За какое время может наполнить этот бак каждая труба, если при совместном действии этих труб в течение 8 мин было заполнено  бака?
бака?
Ответ: 20 мин, 30 мин.
Задача 7. На складе хранилось 500 м3 досок и бруса. После продажи 10 % досок и 15 % бруса осталось 445 м3 пиломатериалов. Сколько кубических метров досок продали? О т в е т: 40 м3.
Приложение 8
Тема 11. Решение задач с литературными и историческими сюжетами.(2ч)
Задача 1. Один небогатый римлянин взял в долг у заимодавца 50 сестерциев. Заимодавец поставил условие: «Ты вернешь мне в установленный срок 50 сестерциев и еще  от этой суммы». Сколько сестерциев должен отдать небогатый римлянин заимодавцу, возвращая долг? (Ответ: 60 сестерциев.)
от этой суммы». Сколько сестерциев должен отдать небогатый римлянин заимодавцу, возвращая долг? (Ответ: 60 сестерциев.)
Задача 2. Некий человек взял в долг у ростовщика 100 рублей. Между ними было заключено соглашение о том, что должник обязан вернуть деньги ровно через год, доплатив еще  суммы долга, но через 6 месяцев должник решил вернуть долг. Сколько рублей он вернет ростовщику? (Ответ: 140 р.)
суммы долга, но через 6 месяцев должник решил вернуть долг. Сколько рублей он вернет ростовщику? (Ответ: 140 р.)
Задача 3. Завещание Бенджамина Франклина: «Препоручаю 1000 фунтов стерлингов бостонским жителям. Если они примут эту тысячу фунтов, то должны поручить ее отборнейшим гражданам, а они будут давать их с процентами по 5 на 100 в год в заем молодым ремесленникам. Сумма эта через 100 лет возвысится до 131 000 фунтов. Я желаю, чтобы тогда 100 000 фунтов употреблены были на постройку общественных зданий, а остальные 31 000 фунтов отданы были в проценты на 100 лет. По истечении второго столетия сумма возрастет до 4061 000 фунтов, из коих 1 061 000 фунтов оставляю в распоряжении бостонских жителей, а 3 000 000 - правлению Массачусетской общины. Далее не осмеливаюсь простирать своих видов». Мы видим, что завещав всего 1000 фунтов, Б. Франклин распоряжается миллионами. Проверьте, не ошибся ли он в своих расчетах.
Ответ: к концу второго столетия эта сумма будет равна 4 142422,7 фунтов. Б. Франклин действительно мог распоряжаться миллионами.
Задача 4. В романе М. Е. Салтыкова-Щедрина «Господа Головлевы» есть такой эпизод: «Порфирий Владимирович сидит у себя в кабинете, исписывая цифирными выкладками листы бумаги. На этот раз его занимает вопрос: «Сколько было бы теперь у него денег, если бы маменька Арина Петровна подаренные ему при рождении дедушкой на зубок 1 00 рублей ассигнациями не присвоила бы себе, а положила бы в ломбард на имя малолетнего Порфирия? Выходит, однако, немного: всего 800 рублей ассигнациями». (предположить, что Порфирию Владимировичу в момент счета было 53 года.) Сколько процентов в год платил ломбард? (Ответ: 4 %.)
Задача 5. В романе М. Е. Салтыкова-Щедрина «Господа Головлевы» сын Порфирия Владимировича Петя проиграл в карты казенные 3000 рублей и попросил у бабушки эти деньги взаймы. Он говорил: «Я бы хороший процент дал. Пять процентов в месяц». Подсчитайте, сколько денег готов вернуть Петя через год, согласись бабушка на его условия.
(Ответ: 4800 рублей.)
Приложение 9
Тема 13. Задачи с параметрами (3ч)
-
Решите уравнение  = 3
= 3
-
Решите уравнение  = 2
= 2
-
Найти все значения а, при которых число х = 2 является корнем уравнения
│х + 2а│•х +1 – а = 0
-
Найти все значения а, при которых число х = - 2 является корнем уравнения
│х - а│•х +1 – 2а = 0
-
Найти все значения а, при которых число х = 1 не является корнем уравнения
│2х + а│• (х 2 + 1) + 3 –2 а = 0
-
Найти все значения а, при которых число х = 2 не является решением неравенства
-
Найти все значения а, при которых число х = - 3 является решением неравенства
-
-│х - 2а│≤ х2
-
Для каждого значения а найдите число корней уравнения │х + 1│= 3 – ах
-
Для каждого значения а найдите число корней уравнения │х - 2│-1 = а -3х
Приложение 10
Тема 14. Решение уравнений, которые встречаются в ОГЭ. (2ч)
Задачи на совместную работу.
Задача 1. Два оператора, работая вместе, могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 3 ч, а второй 12 ч, то они выполнят только 75% всей работы. За какое время может набрать весь текст каждый оператор, работая отдельно?
|
| Всего выполнено, часов | Работает за 1 час |
| 1 | х ч | 
|
| 2 | у ч | 
|
75%=
Ответ:второй оператор за 24ч,первый оператор за 12ч.
Задача 2. На изготовление 231 детали ученик тратит на 11 часов больше, чем мастер на изготовление 462 таких же деталей. Известно, что ученик за час делает на 4 детали меньше, чем мастер. Сколько деталей в час делает ученик?
|
| За час делает , деталь | Всего работает, ч |
| ученик | х | 
|
| мастер | х +4 | 
|

D=289
 не является решением задачи
не является решением задачи

Ответ:за час ученик делает 3 деталей .
Задача 3.Чтобы накачать в бак 117 л воды, требуется на 5 минут больше времени, чем на то, чтобы выкачать из него 96 л воды. За одну минуту можно выкачать на 3 л воды больше, чем накачать. Сколько литров воды накачивается в бак за минуту?
|
| За 1 минуту, л | Вся работа, мин |
| накачать | х | 
|
| выкачать | (х +3) | 
|

 не является решением задачи
не является решением задачи

x
Ответ:за 1 минуту накачивается 9л.
Задача 4. Дима и Саша выполняют одинаковый тест. Дима отвечает за час на 12 вопросов теста, а Саша — на 22. Они одновременно начали отвечать на вопросы теста, и Дима закончил свой тест позже Саши на 75 минут. Сколько вопросов содержит тест?
Ответ :тест содержит 33вопроса.
Задача 5.
Две трубы наполняют бассейн за 8 часов 45 минут, а одна первая труба наполняет бассейн за 21 часов. За сколько часов наполняет бассейн одна вторая труба?
Ответ:наполняет бассейн одна вторая труба за 15 ч.
Задача6. Первая труба пропускает на 2 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объёмом 130 литров она заполняет на 4 минуты?
Ответ:вторая труба пропускает в минуту10л.
Задача7. Две трубы наполняют бассейн за 6 часов 18 минут, а одна первая труба наполняет бассейн за 9 часов. За сколько часов наполняет бассейн одна вторая труба?
Ответ:наполняет бассейн одна вторая труба за 21 ч.
Задача 8.
Игорь и Паша красят забор за 20 часов. Паша и Володя красят этот же забор за 24 часа, а Володя и Игорь — за 30 часов. За сколько часов мальчики покрасят забор, работая втроём?
|
| Один работает, всего, ч | Один работает за 1 час | Всесте работют, ч | Вместе работают за один час |
| Игорь | х | 
| 
20 ч | 
30 ч |  
| 

|
| Паша | у | 
|

| 
|
| Володя | z | 
| 24ч | 
|
Игорь+Паша=20ч
Паша+Володя=24 ч
Игорь + Володя = 30 ч
+
 =
= вместе красят за 16 часов.
вместе красят за 16 часов.







 |f (x)| = g (x), равносильность уравнений |f (x)| = |g (x)| к f (x) = g (x); и f (x) = - g (x),
|f (x)| = g (x), равносильность уравнений |f (x)| = |g (x)| к f (x) = g (x); и f (x) = - g (x), |f (x)| = g (x) к
|f (x)| = g (x) к 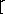 f (x) = g (x);
f (x) = g (x); ]
] 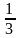
 ] 10. │7x-12│-│7x-1│=1 Ответ:
] 10. │7x-12│-│7x-1│=1 Ответ: 
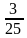 железа, содержание железа в оставшейся руде повысилось на 20%. Определите, какое количество железа осталось еще в руде? (Ответ: 187,5 кг)
железа, содержание железа в оставшейся руде повысилось на 20%. Определите, какое количество железа осталось еще в руде? (Ответ: 187,5 кг) 0,9=4,5 (х+у+5)
0,9=4,5 (х+у+5)
 Ответ:
Ответ: 
 от этой суммы». Сколько сестерциев должен отдать небогатый римлянин заимодавцу, возвращая долг? (Ответ: 60 сестерциев.)
от этой суммы». Сколько сестерциев должен отдать небогатый римлянин заимодавцу, возвращая долг? (Ответ: 60 сестерциев.)  суммы долга, но через 6 месяцев должник решил вернуть долг. Сколько рублей он вернет ростовщику? (Ответ: 140 р.)
суммы долга, но через 6 месяцев должник решил вернуть долг. Сколько рублей он вернет ростовщику? (Ответ: 140 р.) 





















