© 2019 4099 31
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 25.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Все о треугольниках
Категория:
Математика
01.10.2019 21:33
Просмотр содержимого документа
«Все о треугольниках»
ГЕОМЕТРИЯ 7 – 9 КЛАССЫ
Работу выполнила учитель математики Данилина С.Ю.
ТЕМА: «ПОВТОРЕНИЕ. ТРЕУГОЛЬНИКИ.»
- Цели:
-обобщить и систематизировать полученные знания умения и навыки;
-развивать математическое мышление.
ПЛАН
1 Определение треугольника и его элементов.
2 Виды треугольников.
3 Понятие о равных треугольниках .
4 Признаки равенства треугольников .
5 Признаки равенства прямоугольных треугольников .
6 Свойства прямоугольных треугольников .
7 Свойства равнобедренного треугольника.
8 Сумма углов треугольника.
9 Средняя линия треугольника.
10 Теорема Пифагора.
11 Признаки подобия треугольников .
12 Теоремы синусов и косинусов .
13 Формулы нахождения площади треугольника .
ОПРЕДЕЛЕНИЕ
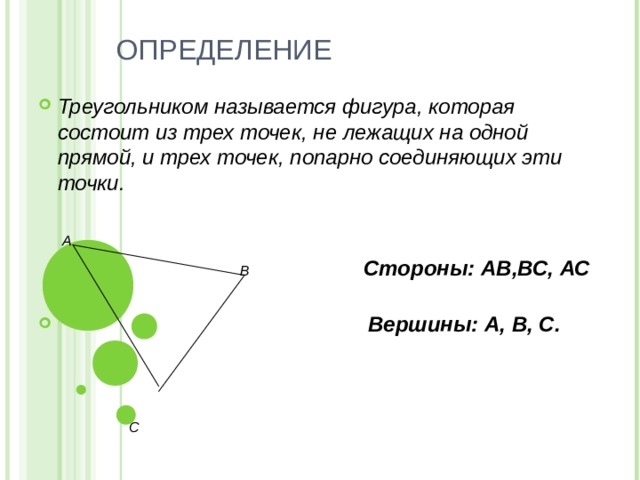
- Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех точек, попарно соединяющих эти точки.
А
В Стороны: АВ,ВС, АС
- Вершины: А, В, С.
С
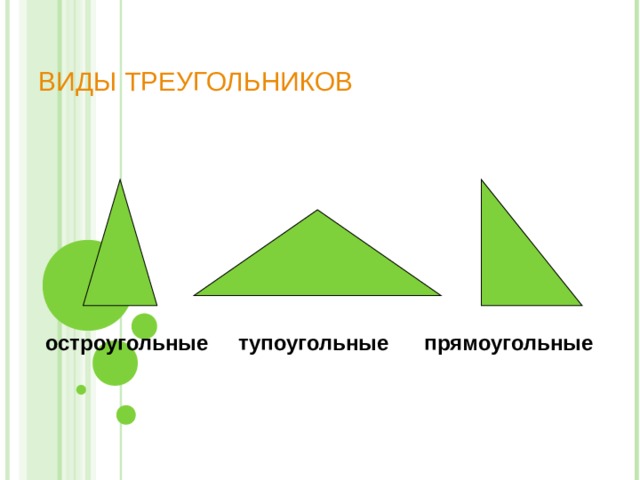
ВИДЫ ТРЕУГОЛЬНИКОВ
остроугольные тупоугольные прямоугольные
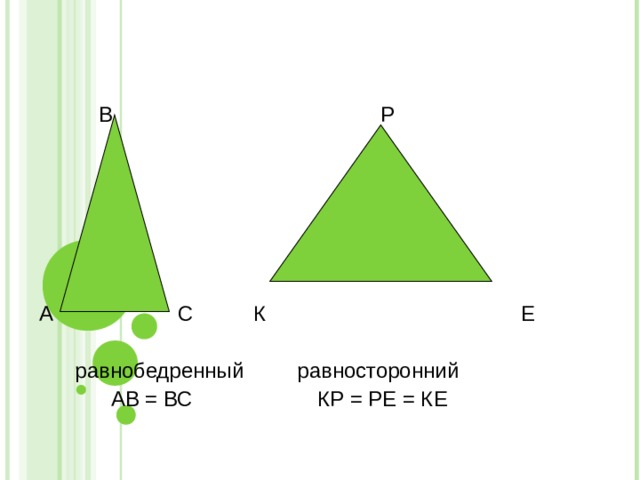
В Р
А С К Е
равнобедренный равносторонний
АВ = ВС КР = РЕ = КЕ
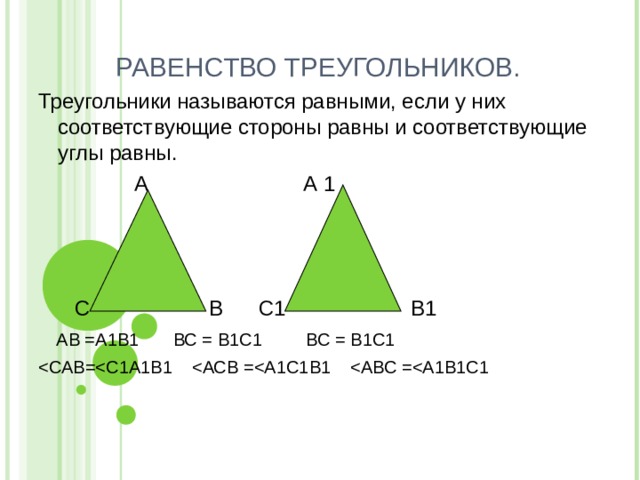
РАВЕНСТВО ТРЕУГОЛЬНИКОВ.
Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны.
А А 1
С В С1 В1
АВ =А1В1 ВС = В1С1 ВС = В1С1
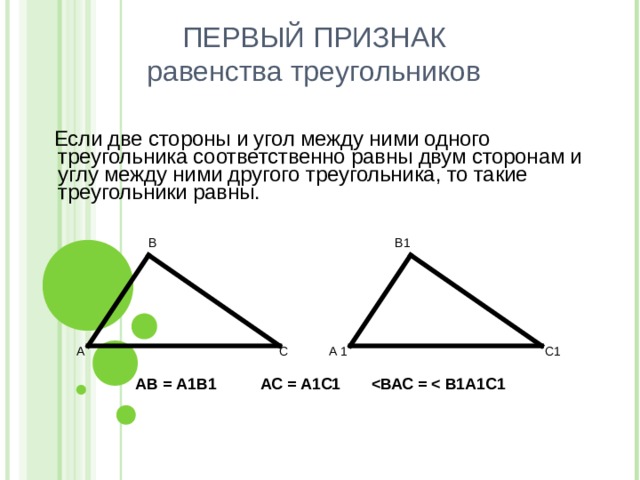
ПЕРВЫЙ ПРИЗНАК равенства треугольников
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
В В1
А С А 1 С1
АВ = А1В1 АС = А1С1 ВАС = В1А1С1
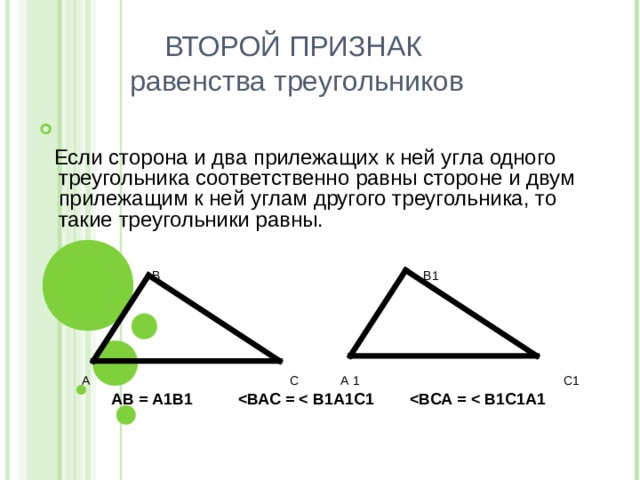
ВТОРОЙ ПРИЗНАК равенства треугольников
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
В В1
А С А 1 С1
АВ = А1В1 ВАС = В1А1С1 ВСА = В1С1А1
ТРЕТИЙ ПРИЗНАК равенства треугольников
- Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
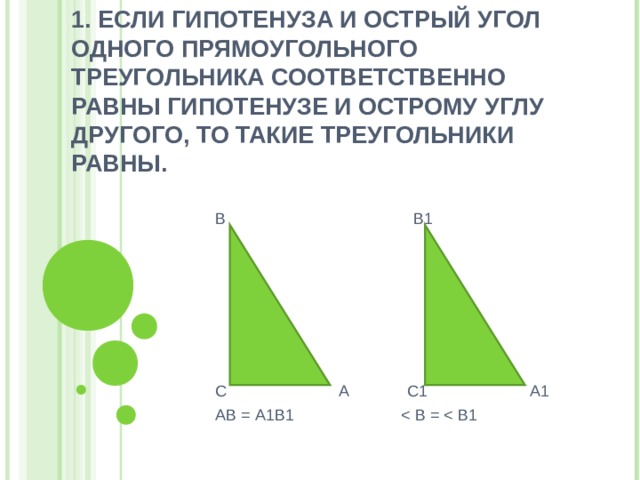
1. ЕСЛИ ГИПОТЕНУЗА И ОСТРЫЙ УГОЛ ОДНОГО ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА СООТВЕТСТВЕННО РАВНЫ ГИПОТЕНУЗЕ И ОСТРОМУ УГЛУ ДРУГОГО, ТО ТАКИЕ ТРЕУГОЛЬНИКИ РАВНЫ.
В В1
С А С1 А1
АВ = А1В1
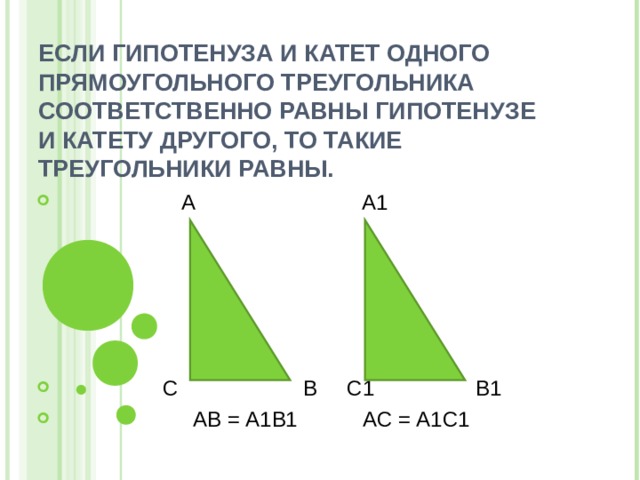
ЕСЛИ ГИПОТЕНУЗА И КАТЕТ ОДНОГО ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА СООТВЕТСТВЕННО РАВНЫ ГИПОТЕНУЗЕ И КАТЕТУ ДРУГОГО, ТО ТАКИЕ ТРЕУГОЛЬНИКИ РАВНЫ.
- А А1
- С В С1 В1
- АВ = А1В1 АС = А1С1
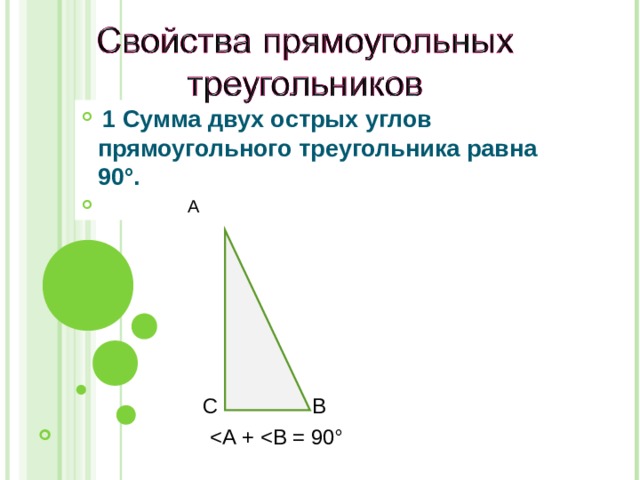
- 1 Сумма двух острых углов прямоугольного треугольника равна 90°.
- А
С В
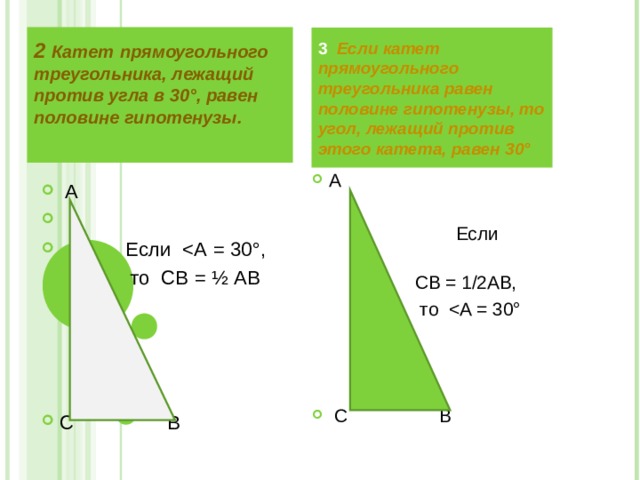
2 Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
3 Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°
- А
Если
СВ = 1/2АВ,
то
- С В
- А
- Если
то СВ = ½ АВ
- С В
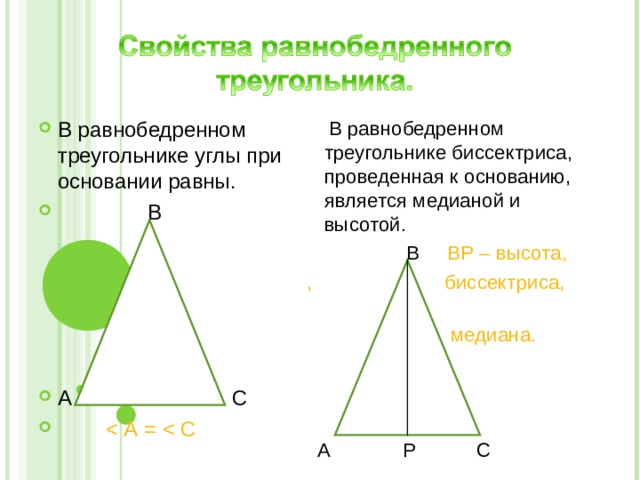
- В равнобедренном треугольнике углы при основании равны.
- В
- А С
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
В ВР – высота,
, биссектриса,
медиана.
А Р С
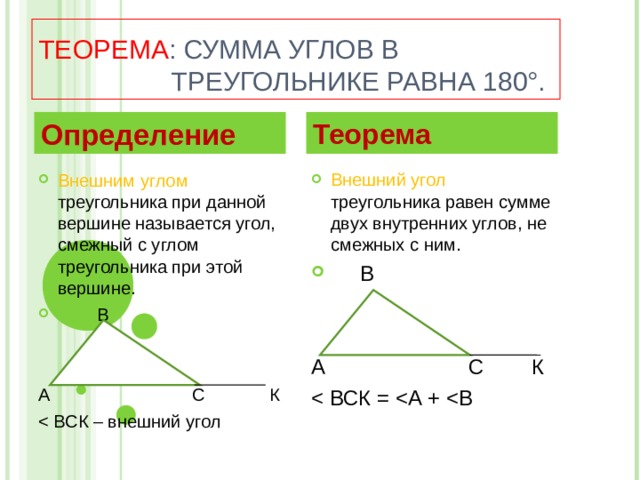
ТЕОРЕМА : СУММА УГЛОВ В ТРЕУГОЛЬНИКЕ РАВНА 180°.
Определение
Теорема
- Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
- В
А С К
- Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине.
- В
А С К
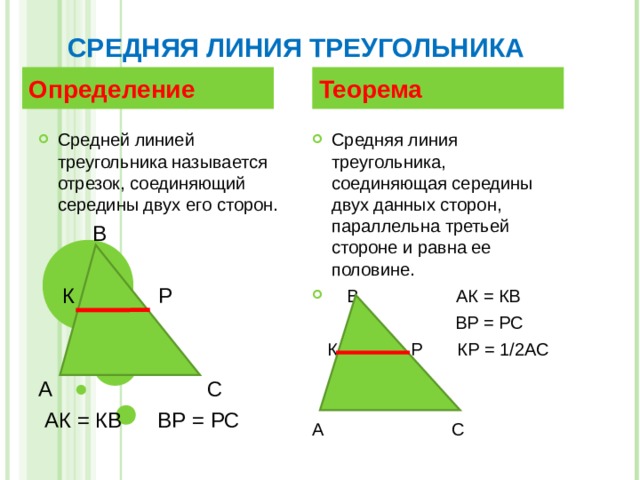
СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА
Определение
Теорема
- Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
В
К Р
А С
АК = КВ ВР = РС
- Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.
- В АК = КВ
ВР = РС
К Р КР = 1/2АС
А С
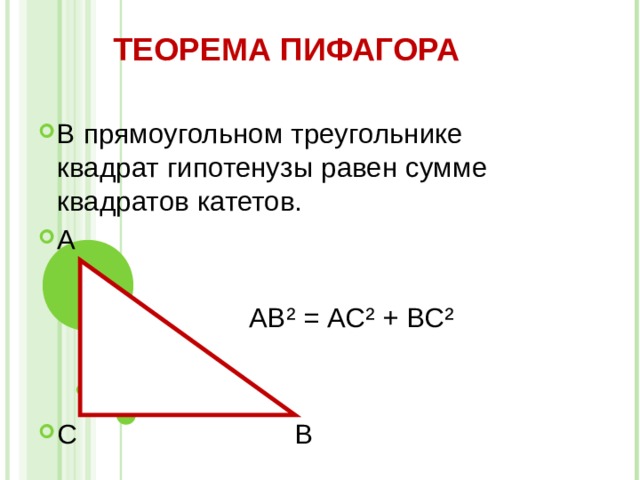
ТЕОРЕМА ПИФАГОРА
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
- А
АВ² = АС² + ВС²
- С В
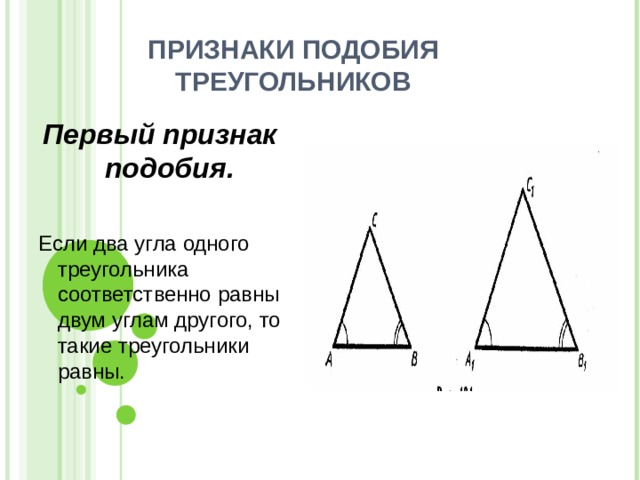
ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ
Первый признак подобия.
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники равны.
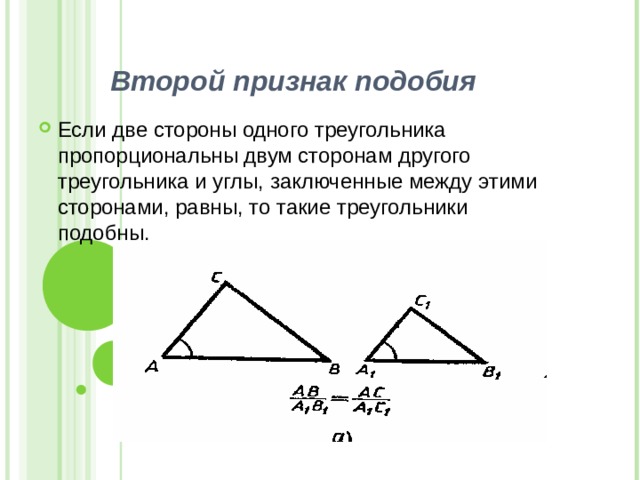
Второй признак подобия
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
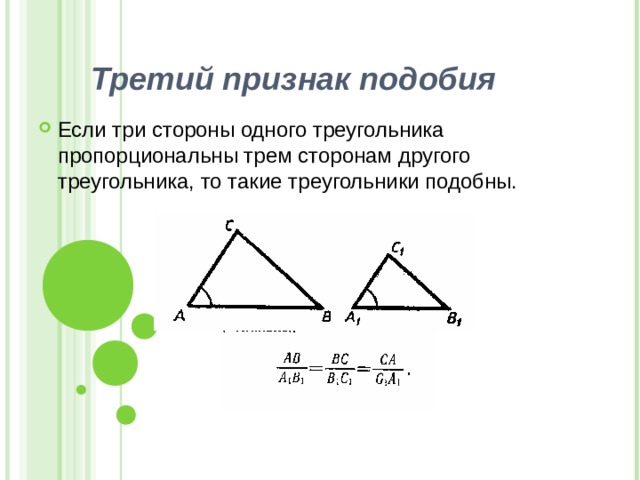
Третий признак подобия
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
- Теорема синусов
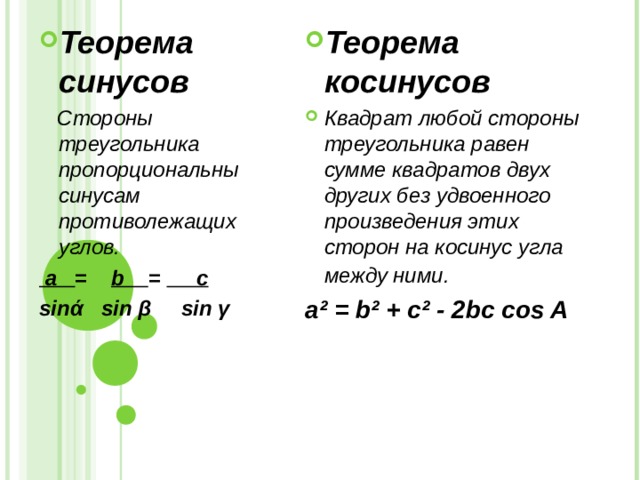
- Теорема косинусов
- Квадрат любой стороны треугольника равен сумме квадратов двух других без удвоенного произведения этих сторон на косинус угла между ними.
Стороны треугольника пропорциональны синусам противолежащих углов.
а = b = c
sin ά sin β sin γ
a ² = b² + c² - 2bc cos A
Формулы нахождения площади треугольника
1 S = ½ ah , h - высота, опущенная на сторону а.
2 S = ½ ab sin γ
3 S =rp, r- радиус вписанной
окружности, p- полупериметр.
4 S = abc , R- радиус описанной
4 R окружности
5 S =√ р (p – a)( p – b )( p – c ),
p- полупериметр
ЛИТЕРАТУРА
- Л.С. Атанасян Геометрия 7-9
- Погорелов Геометрия 7-9
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
Закрыть через 5 секунд
