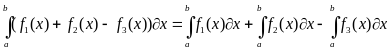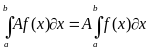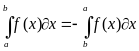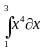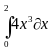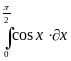Вычисление площади плоской фигуры

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

НОВОСИБИРСКОЙ ОБЛАСТИ

«БАРАБИНСКИЙ МЕДИЦИНСКИЙ КОЛЛЕДЖ»

Рассмотрено на заседании ЦМК

Протокол № ____от________________

Председатель_____________________

МЕТОДИЧЕСКАЯ РАЗРАБОТКА

ПРАКТИЧЕСКОГО ЗАНЯТИЯ ДЛЯ ПРЕПОДАВАТЕЛЯ

Специальность 31.02.01 Лечебное дело

ДИСЦИПЛИНА ЕН.02. МАТЕМАТИКА

Раздел 1. Математический анализ

Тема 1.7. Основы интегрального исчисления. Определённый интеграл

Практическое занятие 7. Вычисление площадей.

Разработчик – преподаватель О.А. Потемкина

2019

Содержание

Методический лист 3

Мотивация 4

Примерная хронокарта 5

Актуализация опорных знаний 6

Самостоятельная работа студентов на практическом занятии 8

Задание для самостоятельной внеаудиторной работы студентов 18

Список использованных источников 18

Приложение 1 19

Выписка из рабочей программы

дисциплины ЕН.02. МАТЕМАТИКА для специальности 31.02.01 Лечебное дело

Наименование разделов и тем	Содержание учебного материала, лабораторные и практические работы, самостоятельная работа обучающихся, курсовая работа (проект)	Объем часов	Уровень освоения
1	2	3	4
Тема 1.7. Основы интегрального исчисления. Определённый интеграл	Содержание учебного материала	2
	Основы интегрального исчисления. Криволинейная трапеция. Определённый интеграл. Свойства определённого интеграла. Формула Ньютона-Лейбница. Методы вычисления определённых интегралов. Применение определённого интеграла к решению прикладных задач в области профессиональной деятельности.		1,2
	Лабораторные работы	‑
	Практические занятия 6. Определённый интеграл. Задачи, решаемые с использованием свойств первообразных и интегралов.	2
	Практические занятия 7. Вычисление площадей.	2
	Практические занятия 8. Вычисление объёмов. Механические и физические приложения определённого интеграла.	2
	Практические занятия 9. Итоговая работа по разделу «Математический анализ»	2
	Контрольные работы	-
	Самостоятельная работа обучающихся Выполнение упражнений. Работа с обучающими и контролирующими тестами на тему «Основы интегрального исчисления». Работа с учебником [1, стр. 88-114]; [1, стр. 116, задание №32, контрольные вопросы].	5

Методический лист

Тип занятия – учебное занятие по закреплению знаний и способов деятельности.

Вид занятия – выполнение упражнений.

Продолжительность – 90 мин.

Цели занятия:

1. Учебные цели:

• сформировать знание об основах интегрального исчисления.

2. Развивающие цели:

• способствовать формированию ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.

3. Воспитательные цели:

• создать условия для формирования ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

Методы обучения: объяснительно-иллюстративный, репродуктивный.

Место проведения занятия: аудитория колледжа.

Интегративные связи: физика, геометрия и все предметы, где используется математический аппарат.

Слайд 1

Мотивация

Трудно назвать научную область, в которой бы не применялись математические методы изучения реальных объектов и процессов. Одним из важнейших разделов математики, используемых для описания и решения прикладных задач, является интегральное исчисление. Примеры практических задач, дают нам ясное представление о значимости определенного интеграла в области физики, геометрии, механики, биологии и экономики. Решение прикладных задач имеет большое воспитательное значение, так как воспитывает умение распознать то или иное математическое понятие в различных ситуациях и позволяет знакомить учащихся с математическим моделированием как методом научного познания окружающего мира.

Интегральное исчисление возникло из рассмотрения большого числа задач естествознания и математики. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

Изучение данной темы позволит выполнить требования государственного образовательного стандарта СПО по специальности 31.02.01 Лечебное дело дисциплина ЕН.02. Математика, а так же будет способствовать формированию ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.

Изучение данной темы, будет способствовать формированию ОК 2.  Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

Примерная хронокарта

№	Этапы занятия	Время (мин)	Цель	Деятельность			Оснащение
				Преподавателя	Студента
1.	Организационный момент	1	Мобилизовать внимание студентов на работу.	Отмечает отсутствующих, контролирует внешний вид, готовность к занятию	Бригадир дает информацию об отсутствующих. Студенты проводят самоконтроль внешнего вида	Журнал
3.	Мотивационный этап, целеполагание	1	Раскрыть практическую значимость темы, способствовать формированию ОК1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.	Сообщает тему занятия, мотивирует ее, устанавливает приоритеты при изучении темы	Слушают, записывают в тетрадь	МП
4.	Актуализация опорных знаний	10	Подготовка к формированию умения использовать при решении задач основные правила и законы интегрального исчисления	Раскрывает новую тему	Слушают, задают вопросы	МП
5.	Выполнение заданий на закрепление знаний и умений	52	Формирование знаний и умения использовать при решении задач основные правила и законы интегрального исчисления, а так же ОК2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество	Курирует работу студентов на всем этапе, исправляет ошибки	Выполняют самостоятельную работу	МП
6.	Задание на предварительный контроль по изученной теме	3	Концентрация внимания	Инструктирует по выполнению самостоятельной работы	Слушают, наблюдают, задают вопросы	МП
7.	Предварительный контроль по изученной теме	20	Предварительный контроль уровня усвоения знаний и умений при решении задач основные правила и законы интегрального исчисления.	Контролирует выполнение студентами заданий, по результатам вносит коррективы	Выполняют задания	МП
8.	Подведение итогов занятия	1	Развитие эмоциональной устойчивости	Объявляет оценки, мотивирует их, выделяет наиболее подготовленных	Слушают, участвуют в обсуждении, задают вопросы	Журнал
9.	Домашнее задание	1,5	Закрепление знаний и умений по изученной теме	Инструктирует по выполнению домашнего задания	Слушают, записывают задание в тетрадь	МП, журнал
10	Организация окончания занятия	0,5	Прививать аккуратность	Контролирует работу по уборке рабочих мест	Убирают рабочее место, сдают оснащение

Слайд 2

Актуализация опорных знаний

1. Дайте определение определённого интеграла

Определенным интегралом в пределах от а до в от функции f(x), непрерывной на отрезке [а, в], называется приращение любой ее первообразной F(x) при изменении аргумента х от значения х=а до х=b

1. Как называется данная формула

2. 

(Данная формула называется формулой Ньютона-Лейбница, ее называют

основной формулой интегрального исчисления).

3. Перечислите свойства определенного интеграла.

1. Определенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определенных интегралов от слагаемых функций: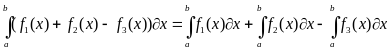

2. Постоянный множитель можно выносить за знак определенного интеграла: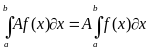

3. При перестановке пределов интегрирования определенный интеграл меняет свой знак на противоположный: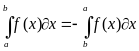

4. Определенный интеграл с одинаковыми пределами равен нулю:

5. Отрезок интегрирования можно разбивать на части:

4. Работа организуется в парах, с последующей взаимопроверкой.

	Вариант 1	Вариант 2
Найдите значение определенных интегралов
1			1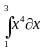
2			2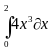
3			3
4			4
5		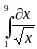	5
6		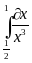	6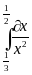
7			7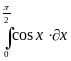

Слайд 3

Ответы к работе в парах:

	1	2	3	4	5	6	7
Вариант 1.		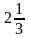33		-10	4
Вариант 2.	48,4	16	0	4	6	1	1

Критерии оценки

«5» – 7 верных ответов;

«4» – 5, 6 верных ответов;

«3» – 3, 4 верных ответов;

«2» –

Самостоятельная работа студентов на практическом занятии

по теме 1.7. Основы интегрального исчисления. Определённый интеграл

Практическое занятие 7. Вычисление площадей

п/№	Наименование этапа	Время этапа	Задание этапа
1	Решение задач	52	Найти площадь фигуры, ограниченной линиями
2	Предварительный контроль	19	Решить предел

Слайд 4

Выполнение заданий на закрепление знаний и умений

На сегодняшнем занятии мы рассмотрим, каким образом с помощью определенного интеграла можно вычислять площадь плоских фигур, и решим несколько конкретных примеров.

1. Основная формула для вычисления площади плоских фигур с помощью определенного интеграла

Рассмотрим постановку задачи о площади криволинейной трапеции.

Вычислить площадь криволинейной трапеции, ограниченной линиями (рис. 1).

Рис. 1. Площадь криволинейной трапеции

Как мы пытались ее решить:

Разбили отрезок [a;b] на n одинаковых отрезков, заменили искомую площадь площадью поступенчастой линии, легко ее сосчитали и получили приближенное решение нашей задачи. Далее устремили  в пределе и получили искомую площадь S.

Ввели обозначение .

Это определенный интеграл. Вот таким образом мы пытались решить задачу. Мы знаем теперь, как приближенно ее решить, знаем обозначения для точного решения, но точного решения еще не знаем.

Затем мы получили точное решение задачи следующим образом: рис. 2:

Рис. 2. Функция S (x)

Ввели функцию S(x). Каждому x на отрезке [a;b] соответствует площадь под соответствующей частью кривой S(x). Так, введенная функция удовлетворяет единственному закону, а именно: каждому x соответствует единственное значение S(x)..

Мы доказали, что производная этой же функции и доказали, что точная площадь вычисляется следующим образом. Надо найти любую первообразную от функции f(x) и взять приращение этих первообразных. То есть взять первообразную в точке b и отнять первообразную в точке a.

И в результате мы получили формулу, которой мы будем пользоваться для вычисления площадей.

Слайд 5

2. Методика нахождения площади на примере

Методику нахождения площади рассмотрим на примере.

Пример 1.

Найти площадь фигуры, ограниченной линиями

Решение.

Вот искомая площадь:

Решение.

Вот искомая площадь:

Рис. 3. Площадь

Вот формула:

Это общая формула. Конкретно к нашему случаю она применима так:
пределы интегрирования .

1 2

Вычислили площадь криволинейной фигуры.

Ответ:

Слайд 6

В следующем примере ищется площадь под параболой.

Пример 2.

Найти площадь фигуры, ограниченной линиями:

Решение.

Схематически изобразим параболу . Корни , ветки направлены вниз (рис. 4)

Рис. 4. Парабола

Применим известную формулу

И применим ее для данной функции и пределов интегрирования ,

4 0

Искомая площадь найдена.

Ответ:

В предыдущих задачах площадь образовывалась с помощью разных кривых, но эта площадь находилась над осью x. В следующей задаче наоборот.

Задания для закрепления и систематизации

Найти площадь фигуры, ограниченной линиями.

1. 

Ответ

1. 0,4;

2. 

3. Случай, если фигура находится под осью Ox

Слайд 7

Пример 3. Найти площадь фигуры, ограниченной линиями

.

Решение.

Посмотрим, что это за фигура. График в пределах от  до 2 расположен под осью Ox (рис. 5).

Рис. 5. График в пределах от до 2

Ясно, что если возьмем определенный интеграл, то мы получим отрицательное число.

Вычисляем.

1. Сначала вычисляем определенный интеграл от π до 2π от подынтегральной функции .

2 

2. Для того чтобы найти площадь, надо взять модуль .

Ответ: 2.

Задания для закрепления и систематизации

Найти площадь фигуры, ограниченной линиями.

Ответ

1. 2;

2. .

4. Общий случай для нахождения площади плоской фигуры, ограниченной двумя кривыми.

Следующее усложнение – искомая площадь расположена между двумя кривыми.

А именно:

Найти площадь фигуры, ограниченной линиями/

Итак, площадь образуют 2 кривые, одна из них может находиться под осью .

Правило!

Площадь фигуры, ограниченной прямыми линиями и графиками функций непрерывных на отрезке [a;b] и таких, что для всех x из отрезка [a;b] вычисляется неравенство вычисляется по формуле:

Слайд 8

Пример 4.

Решение. Для начала построим графики этих линий и поймем, где та площадь, которую нам надо искать.

График квадратичной функции – парабола. Корни – 0, 4, ветви вниз. График прямой – биссектриса первого координатного угла. Вот площадь, которую надо найти:

Рис. 6. Искомая площадь

Но для этого сначала надо найти точки пересечения и решить стандартную задачу.

1. Находим точки пересечения. Для этого решаем систему:

Отсюда получаем квадратное уравнение относительно x:

Мы нашли x, то есть, пределы интегрирования. Это первое важное действие.

2. Теперь стандартное действие:

	3 0

Искомая площадь равна 4,5

Ответ: 4,5

Задания для закрепления и систематизации

Найти площадь фигуры, ограниченной линиями.

1. 

2. ;

3. .

Ответ

1. 2;

2. 

3. 

5. Случай, когда часть площади плоской фигуры лежит под осью

Слайд 9

Во втором примере часть площади находится под осью Ох, но на методику это не влияет.

Пример 5. Требуется найти площадь фигуры, ограниченной линиями

Решение.

Сначала построим графики, посмотрим, какую площадь нам нужно найти. Рис. 7.

Первая функция – парабола, ветви вниз. График второй функции – прямая линия.

Есть две точки пересечения, их придется найти, а именно взять пределы интегрирования, и тогда будем решать задачу по знакомому нам плану.

Рис. 11. Площадь фигуры, ограниченной линиями

Первое действие – найти пределы интегрирования и второе – найти площадь.

Пределы интегрирования найдем из системы:

То есть, пределы интегрирования найдены.

	1 -4

Ответ:

Итак, мы показали, каким образом можно вычислять площади плоских фигур с помощью определенного интеграла.

Задания для закрепления и систематизации

Найти площадь фигуры, ограниченной линиями.

1. 

2. 

Ответ

1. ;

2. .

Дополнительные задания

Вычислить площадь фигуры ограниченной графиками функций

1. 

2. 

3. 

4. 

Ответ

1. 3

2. 4,5

3. 

4. 

Слайд 10

Контролирующий материал

по теме «Вычисление площадей»

Вариант 1

Вычислите площадь фигуры ограниченной линиями

1. 

Вариант 2

Вычислите площадь фигуры ограниченной линиями

1. 

2. 

Эталоны ответов

Номер задания	1 вариант	2 вариант
1
2

Критерии оценки

2 верных ответа– «5»;

1 верный ответ и во втором примере допущена вычислительная ошибка, но верно составлено подынтегральное выражение и найдена первообразная – «4»;

1 верный ответ – «3»;

Не найдено решение в двух задачах – «2».

Слайд 10

Задание для самостоятельной внеаудиторной работы студентов

1. Работа с учебником [1, стр. 88-114]

2. Найти площадь фигуры, ограниченной линиями

1. Найти площадь фигуры, ограниченной линиями

Эталоны ответов

2.

3.

Критерии оценки

2 верных ответа– «5»;

1 верный ответ и во втором примере допущена вычислительная ошибка, но верно составлено подынтегральное выражение и найдена первообразная – «4»;

1 верный ответ – «3»;

Не найдено решение в двух задачах – «2».

Слайд 11

Список использованных источников

1. Гилярова, М. Г. Математика для медицинских колледжей [Текст]. – Ростов н/Д: Феникс, 2011. – 410 с. – (Медицина)

2. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.

3. Михеев, В.С. Математика: учеб. пособие [Текст] / В.С. Михеев [и др.]; под ред. Н.М. Демина. –Ростов н/Д : Феникс, 2009. – 896 с. – (Среднее профессиональное образование).

4. Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.

5. Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.

6. Омельченко, В.П. Математика: компьютерные технологии в медицине: учебник [Текст] / В.П. Омельченко, А.А. Демидова. - Ростов-на-Дону: Феникс, 2010. ‑588с.

7. Омельченко, В.П. Математика: учеб. пособие [Текст] / В.П. Омельченко, Э.В. Курбатова. – Изд. 5-е, стер. – Ростов н/Д: Феникс. 2011. – 380 с. – (Среднее профессиональное образование).

Приложение 1

Таблица неопределённых интегралов