Вычислительные навыки + дидактическая игра

87

Содержание

Введение…………………………………………………………………….4

Глава 1. Теоретические аспекты применения дидактических игр в начальной школе

1. Понятие и виды дидактических игр………………………………….8

2. Возможности использования дидактической игры в процессе обучения математике младшими школьниками………………………………15

Глава 2. Формирование вычислительных навыков у учащихся начальных классов

2.1 Проблема формирования вычислительных навыков младших школьников в современных условиях…………………………………………22

2.2 Методы и приемы вычислительных навыков учащихся начальных классов……………………………………………………………………………38

Глава 3. Опытно-экспериментальное изучение использования дидактической игры как средства формирования вычислительных навыков учащихся начальных классов

3.1 Изучение сформированности вычислительных навыков учащихся начальных классов……………………………………………………………….45

3.2 Использование дидактической игры как средства формирования вычислительных навыков учащихся начальных классов…………………….49

3.3 Анализ опытно-экспериментальной работы………………………...77

Заключение………………………………………………………………..81

Список литературы……………………………………………………….82

Приложения

Введение

Формирование вычислительных навыков - одна из главных задач, которая должна быть решена в ходе обучения детей в начальной школе. Отечественная школа всегда уделяла большое внимание проблеме формирования прочных и осознанных вычислительных умений и навыков, так как содержательную основу начального математического образования оставляют понятия числа и четырех арифметический действий. Формирование вычислительных умений и навыков - сложный длительный процесс, его эффективность зависит от индивидуальных особенностей ребенка, уровня его подготовки и организации вычислительной деятельности. На современном этапе развития начального образования необходимо выбирать такие способы организации вычислительной деятельности младших школьников, которые способствуют не только формированию прочных осознанных вычислительных умений и навыков, но и всестороннему развитию личности ребенка. Одним из таких способов является дидактическая игра.

Методисты рассматривают игру как важнейший метод обучения в начальной школе. Игра не является развлекательным средством – это обычное упражнение, облеченное в занимательную форму. Содержание игры служит выполнению учебной задачи. Игра требует от учащихся сообразительности, внимания, учит выдержке, вырабатывает умение быстро ориентироваться, находит правильное решение, развивает и повышает интерес к предмету.

Наличие различных по сложности и содержанию игровых предметов позволяет учитывать индивидуальные особенности учащихся, повышает уровень знаний.

Проблемы дидактической игры рассматривали такие педагоги и психологи как : Ш. Амонашвили, О. С. Газман, Е. В. Карпова, С. Сорокина, А.В. Запорожец и другие.

Проблема исследования – выявление возможности использования дидактической игры как средства формирования вычислительных навыков учащихся начальных классов;

Цель состоит в решении данной проблемы;

Объект – процесс использования дидактической игры на уроках в начальной школе;

Предмет – возможности использование дидактической игры как средства формирования вычислительных навыков учащихся начальных классов;

Задачи: 1. Изучить психолого-педагогическую литературу по теме исследования;

2. Раскрыть понятие и виды дидактических игр;

3. Рассмотреть применение дидактических игр на уроках математики в начальной школе;

4. Изучить систему формирования вычислительных навыков младших школьников;

5. Изучить использование дидактической игры как средства формирования вычислительных навыков на уроках математики в начальных классах;

6. Опытно-экспериментальным путем проверить эффективность использования дидактической игры как средства формирования вычислительных навыков на уроках в начальной школе.

Методы исследования: анализ психолого-педагогической литературы, наблюдение, анкетирование, анализ полученных результатов.

В качестве гипотезы можно выдвинуть такое утверждение, что если в процессе обучения систематически и последовательно использовать дидактическую игру при формировании вычислительных навыков учащихся начальных классов, то можно добиться повышения успеваемости младших школьников.

2. Рассмотреть процесс формирования вычислительных навыков младших школьников в современных условиях; 3. Изучить систему формирования вычислительных навыков младших школьников; 4. Рассмотреть приемы формирования вычислительных навыков на уроках математики. Гипотеза исследования: правильное выделение стадий в формировании вычислительных навыков позволит учителю управлять процессом усвоения учащимися вычислительного приема, постепенного свертывания выполнения операций, образования вычислительных навыков.

Практическая значимость исследования заключается в том, что разработана система игр с целью использования в педагогическом процессе, как средства формирования вычислительных навыков учащихся начальных классов, которая апробирована и подтверждена результатами экспериментальной работы, и рекомендована учителям начальных классов.

База исследования: 3 «Б» класс МОУ ДСОШ № 2, Домбаровского района, Учитель Сарсекенова Ханзиля Жеткергеновна, учитель 1 категории, стаж работы 11 лет.

Структура исследования:

Исследование состоит из введения, трех глав, заключения, списка литературы и приложения.

Во введении обосновывается актуальность темы, определяются проблема, цель и задачи, объект, предмет, гипотеза и методы исследования.

В первой главе «Теоретические аспекты применения дидактических игр в начальной школе» рассматриваются понятие и виды дидактических игр, возможности использования дидактической игры в процессе обучения математике младшими школьниками.

Во второй главе «Теоретические аспекты формирования вычислительных навыков у детей младшего школьного возраста» изучается проблема формирования вычислительных навыков младших школьников в современных условиях, система формирования вычислительных навыков младших школьников, определяется методика работы по формированию приемов вычислительных навыков на уроках математики

В третьей главе «Опытно-экспериментальное изучение использования дидактической игры как средства формирования вычислительных навыков учащихся начальных классов» представлены количественные и качественные результаты опытно-экспериментальной работы.

В заключении изложены основные выводы исследования. Список литературы состоит из источников.

Положения, выносимые на защиту 1. Одной из важнейших задач обучения математике младших школьников является формирование у них вычислительных навыков, основу которых составляет осознанное и прочное усвоение приемов устных и письменных вычислений. 2. Использование дидактической игры как средства формирования вычислительных навыков позволит учителю управлять процессом усвоения учащимися вычислительного приема, постепенного свертывания выполнения операций, образования вычислительных навыков.

Глава 1. Теоретические аспекты применения дидактических игр на уроках в начальной школе

1.1 Понятие и виды дидактических игр

Одна из главных сфер воспитания детей до школы и в младшем школьном возрасте – игра. Игра – наиболее доступный для детей вид деятельности, способ переработки полученных из окружающего мира впечатлений, знаний.

Первостепенная роль игры в формировании личности ребенка показана в трудах Н.К.Крупской, А.С.Макаренко, Е.А.Аркина, Р.И.Жуковской др. педагогов.

Дидактическая игра представляет собой ряд последовательно выполняемых операций, включенных в игровую задачу. По определению А.Н.Леонтьева эти игры, наряду с играми-драматизациями, являются рубежными, переходными к играм, характерным для школьного периода или к неигровой учебной деятельности, которую они прямо подготавливают .

Рассмотрим более подробно дидактические игры.

Дидактические игры - это разновидность игр с правилами, специально создаваемых педагогикой в целях обучения и воспитания детей. Они направлены на решение конкретных задач обучения детей, но в то же время в них проявляется воспитательное и развивающее влияние игровой деятельности. Необходимость использования дидактических игр как средства обучения детей в младшем школьном возрасте определяется рядом причин:

Игровая деятельность как ведущая в дошкольном детстве еще не потеряла своего значения(не случайно поэтому многие дети приносят
в школу игрушки). Можно согласиться с выводами Л.С.Выготского,
который писал, что «в школьном возрасте игра не умирает, а
проникает в отношения к действительности». Она имеет свое
внутреннее продолжение в школьном обучении и в труде»..Отсюда следует, что опора на игровую деятельность, игровые формы и приемы - это важный и наиболее адекватный путь включения детей в
учебную работу.

Освоение учебной деятельности, включение детей в нее идет медленно (многие дети вообще не знают, что такое «учиться»).

Имеются возрастные особенности детей, связанные с недостаточной устойчивостью и произвольностью внимания, преимущественно непроизвольным развитием памяти, преобладанием нагляднообразного типа мышления. Дидактические игры как раз способствуют развитию у детей психических процессов.

4. Недостаточно сформирована познавательная мотивация. Основная трудность в начальный период обучения заключается в том, что мотив, с которым ребенок приходит в школе, не связан с содержанием
той деятельности, которую он должен выполнить в школе.

Мотив и содержание учебной деятельности не соответствуют друг другу. Побуждать к учению должно то содержание, которому ребенка учат в школе. Существуют значительные трудности адаптации при поступлении ребенка в школу (освоение им новой роли - роли ученика, установление взаимоотношений со сверстниками и учителями). Дидактическая игра во многом способствует преодолению указанных трудностей.

Е. В. Карпова оценивая роль дидактической игры, подчеркивал: «Нам необходимо добиться того, чтобы дидактическая игра была не только формой усвоения отдельных знаний и умений, но и способствовала бы общему развитию ребенка» [11; 147].

А.И.Сорокина выделяет следующие виды дидактических игр: игры-путешествия, игры-поручения, игры-предположения, игры-загадки, игры-беседы.

Охарактеризуем кратко каждый вид.

Игры-путешествия призваны усилить впечатление, обратить внимание детей на то, что находится рядом. Они обостряют наблюдательность, обличают преодоление трудностей. В этих играх используются многие способы раскрытия познавательного содержания в сочетании с игровой деятельностью: постановка задач, пояснение способов ее решения, поэтапное решение задач и т.д.

Игры поручения по содержанию проще, а продолжительности короче. В основе лежат действия с предметами, игрушками. Словесные поручения.

Игры предложения («что было бы») Перед детьми ставится задача и создается ситуация, которая требует осмысления последующего действия. При этом активизируется мыслительная деятельность детей, они учатся слушать друг друга.

Игры-загадки. В основе лежат проверка знаний, находчивость. Разгадывание загадок развивает способность к анализу, обобщению, формирует умение рассуждать, делать выводы.

Игры-беседы. В основе их лежит общение. Основным является непосредственность переживаний, заинтересованность, доброжелательность. Такая игра предъявляет требования к активизации эмоциональных и мыслительных процессов. Она воспитывает умение слушать вопросы и ответы, сосредотачивать внимание на содержании, дополнять сказанное, высказывать суждения. Познавательный материал для проведения этого вида игр должен даваться в оптимальном объеме, чтобы вызвать интерес детей. Познавательный материал определяется темой, содержанием игры. Игра, в свою очередь, должна соответствовать возможностям усвоения интереса детей и свертывания игровых действий.

Дидактическая и игра имеет определенную структуру. Структура - это основные элементы, характеризующие игру как форму обучения и игровую деятельность одновременно. Выделяются следующие структурные составляющие дидактической игры: 1) дидактическая задача; 2) игровая задача; 3) игровые действия; 4) правила игры; 5) результат (подведение итогов).

Дидактическая задача определяется целью обучающего и воспитательного воздействия. Она формируется педагогом и отражает его обучающую деятельность. Так, например, в ряде дидактических игр в соответствии с программными задачами соответствующих учебных предметов закрепляется умение составлять из букв слова, отрабатываются навыки счета и т.д.

Игровая задача осуществляется детьми. Дидактическая задача в дидактической игре реализуется через игровую задачу. Она определяет игровые действия, становится задачей самого ребенка. Самое главное: дидактическая задача в игре преднамеренно замаскирована и предстает перед ребенком в виде игрового замысла (задачи).

Игровые действия - основа игры. Чем разнообразнее игровые действия, тем интереснее для детей сама игра и тем успешнее решаются познавательные и игровые задачи. В разных играх игровые действия различны по их направленности и по отношению к играющим. Это, например, могут быть ролевые действия, отгадывание загадок, пространственные преобразования и т.д. Они связаны с игровым замыслом и исходят от него. Игровые действия являются средством реализации игрового замысла, но включают и действия, направленные на выполнение дидактической задачи.

Правила игры, их содержание и направленность обусловлены общими задачами формирования личности ребенка, познавательным содержанием, игровыми задачами и игровыми действиями. Правила содержат нравственные требования к взаимоотношениям детей, к выполнению ими норм поведения. В дидактической игре правила являются заданными. С помощью правил педагог управляет игрой, процессами познавательной деятельности, поведением детей. Правила влияют и на решение дидактической задачи - незаметно ограничивают действия детей, направляют их внимание на выполнение конкретной задачи учебного предмета.

Подведение итого (результатов) - проводится сразу по окончании игры. Это может быть очесов; выявление детей, которые лучше выполнили игровое задание; определение команды-победительницы и т.д. Необходимо при этом отметить достижения каждого ребенка, подчеркнуть успехи отстающих детей.

При проведении игры необходимо сохранить все структурные элементы, поскольку именно с их помощью решаются дидактические задачи.

Основными функциями дидактической игры являются:

1. функция формирования устойчивого интереса к учению и снятию напряжения, связанного с процессом адаптации ребенка к школьному режиму;

1. функция формирования психических новообразований;

1. функция формирования собственно учебной деятельности;

2. функция формирования общеучебных умений, навыков учебной
   самостоятельной работы;

3. Функция формирования навыков самоконтроля и самооценки;

4. Функция формирования адекватных взаимоотношений и освоение социальных ролей.

Организовать и провести дидактическую игру - задача сложная для педагога.

Можно выделить следующие основные условия проведения дидактической игры:

1. Наличие у педагога определенных знаний и умений относительно дидактических игр.

1. Выразительность проведения игры. Это обеспечивает интерес детей, желание слушать, участвовать в игре.

1. Необходимость включения педагога в игру. Он является и участником и руководителем игры. Педагог должен обеспечить поступательное развитие игры в соответствии с учебными и воспитательными задачами, но при этом не оказывать давление, выполнять второстепенную роль, незаметно для детей направлять игру в нужное русло.

2. Необходимо оптимально сочетать занимательность и обучение. Проводя игру, педагог должен постоянно помнить, что он дает детям сложные учебные задания, а в игру их превращает форма их
   проведения - эмоциональность, легкость, непринужденность.

3. Средства и способы, повышающие эмоциональное отношение детей к игре, следует рассматривать не как самоцель, а как путь, ведущий к
   выполнению дидактических задач.

4. Между педагогом и детьми должны быть атмосфера уважения, взаимопонимания, доверия и сопереживания.

5. Используемая в дидактической игре наглядность должна быть простой и емкой.

По возможности надо стремиться к тому, чтобы в игре участвовал каждый ребенок. Поэтому если игровую деятельность осуществляет часть детей, то остальные должны исполнять роль контролеров, судей, то есть тоже принимать участие в игре. Обязательно нужно обратить внимание на проявление поведения детей и качеств их личности в игре: как проявлялась взаимовыручка в игре, настойчивость в достижении цели. Постоянно демонстрируйте детям их достижения. Игра должна отвечать следующим требованиям: быть интересной, доступной, включать разные виды деятельности детей.

Реализуя содержание игры, игровые задачи, используя игровые действия, педагог учит детей общению, жизни в коллективе сверстников. Среди людей, помогает овладевать коммуникативными умениями.. В игре педагог создает ситуацию, обращенную к разуму и сердцу ребенка, создает «модель поведения» и через образ учит с кого брать пример и как об этом рассказывать.

Источником содержания дидактических игр является сама жизнь с богатством и разнообразием ее явлений. Питает игру и художественная литература для детей. В произведениях К.Чуковского, С.Маршака, сказах П.Бажова сказочное сочетается с реальностью, разворачиваются чудесные приключения, необычайные истории, совершаются необыкновенные путешествия. В поступках и действиях героев сказок заложены многие моральные основы: находчивость, упорство, трудолюбие, доброта, бескорыстная помощь. На близком и понятном содержании сказок, на примерах действий, отношений героев раскрывается и для детей характер отношений, который они в силу подражания незаметно усваивают.

Источником, обогащающим игру, являются наглядно-изобразительные средства, в первую очередь, картинки. Истории в картинках дает возможность легко переводить изображения в слова, иногда в рассказ, который развивает речь ребенка и его коммуникативные умения. На роль картинки указывал еще К.Д.Ушинский. Он писал: «Учите ребенка каким-нибудь неизвестным ему словам, и он будет долго и напрасно мучиться над ними, но свяжите с картинками двадцать таких слов и ребенок усвоит их на лету. Вы объясняете ребенку очень простую мысль, а он вас не понимает; вы объясняете ребенку тому же ребенку сложную картину, и он вас понимает быстро...» [23; 307] Показывание картинок и рассказы по ним учат ребенка говорить, высказывать свои мысли вслух, учат ребенка слушать другого, уметь ему сопереживать.

У детей посредством игры нужно развивать душевную чуткость, чтобы они по выражению лица, по отдельным признакам, действиям могли заметить, обрадован или огорчен товарищ, близкие, мог проникнуться сопереживанием, порадоваться, огорчиться, помочь. Нельзя, чтобы у детей развивалось равнодушие. Проникнуть в мир переживаний детям помогает картинка, слово. В игре картинка - участник игры.

Сейчас ребенок получает много информации - из радио и телевизионных передач, книг. Ценность дидактических игр заключается в том, что они как бы побуждают потребность рассказать о чем-то близком для ребенка. Например, в игре «Что бы ты пожелал себе?» мальчик с чувством горечи отвечает: «Не знаю, папа говорит, что я «слабак» и не могу быть летчиком-испытателем, а я так бы хотел...». Девочка, высказывая пожелание для мамы, говорит: «Пусть мама будет здоровая, веселая и пусть ни с кем не ссорится...»

Итак, применяя дидактические игры во время обучения, педагог делает урок ярким, запоминающимся, развивает познавательный интерес, память, воображение и внимание ребенка на уроках.

1. Возможности использования дидактической игры в процессе обучения математике младшими школьниками

Одним из эффективных средств формирования вычислительных навыков учащихся являются дидактические игры, разработанные с учетом возрастных и индивидуальных особенностей учащихся.

Дидактическая игра – это одна или несколько математических задач, предлагаемых в занимательной форме и, как правило, с элементами соревнования. Они не только позволяют проверить умения учащихся выполнять математические действия, анализировать, сравнивать, подмечать закономерности, но и значительно повысить интерес к математике, снять усталость, а также способствует развитию внимания, сообразительности, активизирует чувство соревнования, взаимопомощи. Наиболее целесообразно использовать дидактические игры и игровые ситуации при проверке результатов обучения, выработке навыков, формирование умений.

Можно провести условную классификацию этих игр, взяв за главный отличительный признак основную цель игры:

1. Игры, направленные на формирование и совершенствование навыков устного счета.

2. Игры, направленные на актуализацию теоретических знаний («Поле Чудес», «Счастливый случай»).

3. Игры по формированию вычислительных навыков и умений («Домино»).

4. Контрольно-обобщающие игры.

5. Игры, направленные на составление задач по рисункам, таблицам, символическим записям.

6. Игры, направленные на самостоятельное формулирование условий и требований задачи, закодированные в данных схемах или знаках.

В процессе проведения дидактических игр при формировании вычислительных навыков нужно определить требование к организации:

1. Дидактическая игра должна иметь четкую структуру, все элементы которой взаимосвязаны между собой. Без игрового замысла и игровых действий, без правил дидактическая игра невозможна, иначе она превращается в выполнение указаний, упражнений. Определенный результат, являющийся финалом игры, придает ей законченность, является показателем уровня достижений учащихся.

2. Правила игры должны быть простыми, а математическое содержание доступным пониманию учащихся.

3. Дидактический материал, используемый во время игры, должен быть удобен в применении, иначе игра не даст должного результата.

4. Необходимо следить за сохранением интереса учащихся к игре, добиваться того, чтобы каждый ученик был ее активным участником, иначе игра теряет свое развивающее значение.

5. Игровой момент на уроке математики должен иметь определенную меру.

6. Математическая сторона содержания игры должна быть на первом плане. Только тогда игра будет выполнять свою роль в математическом развитии детей и воспитании интереса их к математике.

Игровые формы занятий наиболее эффективны при проверке результатов обучения, выработке навыков, формированию умений.

Дидактическая игра реализует обучающую, развивающую функции.

Обучающий характер достигается за счёт проблемного содержания игры.

Достоинством дидактической игры является экономия времени обучения. Игровое обучение вызывает усиление познавательного интереса к предмету.

Развивающий потенциал игры заключается в том, что игра позволяет избавиться от стереотипа, служит для активизации резервных возможностей.

Наряду с обучающей и развивающей функциями дидактическая игра реализует функцию воспитания, снимает напряжённость, страх, повышает самооценку, позволяет проверить себя в различных ситуациях.

Важным условием, способствующим успешному проведению дидактических игр является педагогическое руководство ими. Роль учителя остаётся значительной на всем протяжении игры. Для учащихся начальных классов эмоциональная сторона организации игры - важное условие. Педагог своим поведением, эмоциональным настроем должен вызвать у ребенка положительное отношение к игре. Необходима доброжелательность взрослого, благодаря которой и появляется сотрудничество, обеспечивающее желание ребенка действовать вместе со взрослым и добиваться положительного результата.

Роль педагога в дидактической игре двойственна: с одной стороны, он руководит познавательным процессом, организует обучение детей, а с другой выполняет роль участника игры, партнера, направляет каждого ученика на выполнение" игровых действий, а при необходимости дает образец поведения в игре. Участвуя в игре, педагог одновременно следит за выполнением правил. Место в уроке и характер игры определяет учитель, исходя из работоспособности класса, из сложности того материала, с которым будут работать учащиеся. Руководство игрой требует от педагога знания особенностей каждого ребенка, понимание его поведения, интересов, способностей. В классе все дети разные: общительные и замкнутые, активные и молчаливые, не всегда организованные и, наоборот, спокойные, дисциплинированные. У всех разные способности: одни учащиеся проявляют творчество и самостоятельность, выполняют как главные, так и второстепенные роли, другие, наоборот, безынициативные, с низким уровнем умений и навыков.

Педагог, соблюдая дидактические принципы и внимательно, продуманно организуя дидактическую игру на уроке, обеспечивает прочное усвоение знаний и умений всем классом.

Дидактическая игра - ценное средство воспитания умственной активности учащихся. По характеру познавательной деятельности дидактические игры можно отнести к следующим группам:

1 Игры, требующие от детей исполнительной деятельности. С помощью этих игр дети выполняют действия по образу. Например, составляют узор по образу и др.

2 Игры, в ходе которых дети выполняют воспроизводящую деятельность. К этой группе относится большое число игр, направленных на формирование вычислительных навыков. Пример такой игры «Определи курс движения самолета». Учитель обращается к детям: «Летчик-командир придумал для вас задание. Он наметил курс движения самолета из одного города в другой. Самолет должен лететь над городами в указанном порядке о меньшего числа (номера) к большему. Номер каждого города зашифрован (записан) примером. Чтобы расшифровать номера городов, надо решить правильно примеры. Я буду выполнять роль летчика-командира, а вы - роль летчиков-курсантов (учеников). Игровое действие выполняется поэтапно в соответствии с заданием: а) сначала дети расшифровывают номера городов (решают примеры); б) далее дети называют номера городов по порядку от меньшего числа к большему; в) потом они поочередно показывают линиями путь движения самолета; г) затем дети по цепочке рассказывают в каком направлении двигался самолет. На доске учащиеся записывают ответы примеров и показывают мелом путь движения самолета (можно перемещать рисунок самолета от одного примера к другому). Аналогично дети могут определять маршрут движения пароходов, машин (от дальних пунктов к ближайшим - от больших чисел к меньшим).

З.Игры, в которых запрограммирована контролирующая деятельность учащихся. Например, игра «Контролеры». Учитель распределяет детей на две команды. От каждой команды вызывается к доске по 1 контролеру. Они следят за правильностью ответов: одни -за первой командой, другой - за второй. По сигналу учителя (движению руки) ученики первой команды делают несколько ритмичных наклонов влево и вправо и считают про себя. По сигналу учителя - хлопку они называют хором число выполненных наклонов (например, 6-прибавил1; 7-прибавил 2; 8-прибавил 3). Затем они называют число выполненных ими наклонов. По числу наклонов, выполненных учениками первой и второй команды, называется состав числа. Учитель говорит: «8 - это...», ученики продолжают: «5 и 3». Контролеры показывают зеленые круги, если они согласны с ответом. Аналогично анализируется состав числа на основе хлопков, выполненных учениками двух команд. Выигрывает та команда, которая не допустит ни одной ошибки или сделает меньшее число ошибок.

4.Игры, с помощью которых дети осуществляют преобразующую деятельность. Например, игра «Числа - перебежчики». Учитель делит класс на команды. Сначала дается задание первой команде, учитель выдает им карточки с цифрами и знаками действий. Дети по заданию учителя составляют пример на сложение вида 1+3=4. Учитель предлагает «числам» (ученикам) перебежать так, чтобы получился другой пример на сложение с этими числам». Лет» составляют другой «живо»» пример на сложение, например 3+1=4. аналогично, перебегая на другие и меняя знаки действий, дети составляют другие примеры вида: 4=1+3; 4-3=1; 4-t=3. все примеры составленные детьми записывает на доске учитель. Аналогичные действия выполняет другая команда.

З.Игры, включающие элементы поисковой деятельности. Так, в игре «Угадайка» дети сами формируют правило по рисунку и схемам примеры на сложение. Рассматривая рисунок, дети вставляют в рамку столько точек сколько матрешек и коней на каждом рисунке. За"!ем по .рисунку и схеме они составляют пару примере» на сложение (3+2—5, 2 0=5). 'Проведение игры требует большого мастерства от учителя. Перед игрой учитель должен доступно изложить ее сюжет, распределить роли, поставить пред. детьми. познавательную задачу; подготовить необходимое оборудование, сделать нужные записи на доске.

Если дидактическая задача скрыта сюжетом, ролью, игровым действием, то в ходе беседы с детьми учитель должен обратить- внимание на это,

В игре в той или иной роли должен участвовать каждый ученик класса: Если у доски работает небольшое количество учащихся; то остальные должны выполнять роли контролеров, студентов, учиться и т.д. игра может быть проведена на любом этане урока на уроке каждого типа. Если игра используется на уроке объяснения нового материала, то в ней должны быть запрограммированы практические действия детей с группами предметов или рисунками. На уроках закрепления материала важно применять игры на воспроизведение свойств действий и вычислительных приемов. В этом случае следует ограничить использование средств наглядности, а усилить внимание к громкому проговариванию правила, свойства, вычислительного приема.

В системе уроков по теме важно подобрать игры на разные виды деятельности: исполнительскую, воспроизводящую, контролирующую и поисковую. В игре следует придумывать не только характер деятельности детей, но и организующую сторону, характер управления игрой, С этой цепью следует использовать такие "простейшие" средства "обратной связи, как сигнальные карточки (кружок зелёного цвета с одной стороны и кружок красного - с другой) или разрезные цифры Сигнальные карточки служат средством активизации детей в игре. В большинстве игр полезно вносить элементы соревнования, что также повышает активность детей в процессе обучения математики. Чтобы не нарушать впечатления от игры, ошибки учащихся надо анализировать не в ходе игры, а в конце.

С помощью дидактической игры решаются различные познавательные задачи. На примере игры «Вполоборота» можно поработать над развитием математической речи у учащихся (работа над понятиями «толстый-тонкий» и т.п.). Игра «Найди спрятанную карточку», «Лучший разведчик» помогает формировать у детей пространственные представления.

При изучении чисел первого десятка используются такие игры, с помощью которых дети наглядно осознают приемы образования каждого последующего и предыдущего числа. В ходе игры «Составим поезд» учитель предлагает детям сосчитать число вагонов слева-направо и подводит их к выводу: считать можно в любом направлении, но при этом важно не пропустить ни одного предмета и не сосчитать его дважды.

При изучении нумерации в пределах 10 можно проводить игры «Лучший счетчик», «Хлопки», «Найди себе пару», «Курица и цыплята», где важно довести до понимания детей, что последнее названное при счете число обозначает общее количество предметов группы. По теме «Сложение и вычитание в пределах 10» можно использовать большое число нгр направленных на формирование вычислительных навыков. Например, игра «Составим поезд», в процессе которой дети знакомятся с приемами прибавления и вычитания в пределах 10.

Таким образом, проводить игры можно используя местный материал и учитывая индивидуально-психологические особенности детей. Применяются дидактические игры и при формировании вычислительных навыков.

Глава 2 Формирования вычислительных навыков у учащихся

начальных классов

2.1 Проблема формирования вычислительных навыков младших школьников в современных условиях

Одной из важнейших задач обучения математике младших школьников является формирование у них вычислительных навыков, основу которых составляет осознанное и прочное усвоение приемов устных и письменных вычислений. Вычислительная культура является тем запасом знаний и умений, который находит повсеместное применение, является фундаментом изучения математики и других учебных дисциплин. В век компьютерной грамотности значимость навыков письменных вычислений, несомненно, уменьшилась. Использование ЭВМ во многом облегчает процесс вычислений. Но пользоваться техникой не имея вычислительных навыков невозможно, да и микрокалькулятор не всегда может оказаться под рукой. Следовательно, владение вычислительными навыками необходимо. Научиться быстро и правильно выполнять письменные вычисления важно для младших школьников как в плане продолжающейся работы с числами, так и в плане практической значимости для дальнейшего обучения. Поэтому вооружение учащихся прочными вычислительными навыками продолжает оставаться серьезной педагогической проблемой. Но надо выявить, каковы педагогические условия формирования вычислительных навыков в начальной школе. Проблема формирования у учащихся вычислительных умений и навыков всегда привлекала особое внимание психологов, дидактов, методистов, учителей. В методике математики известны исследования Е.С. Дубинчук, А.А. Столяра, С.С. Минаевой, Н.Л. Стефановой, Я.Ф. Чекмарева, М.А. Бантовой, М.И. Моро, Н.Б. Истоминой, С.Е. Царевой и др. Глубоко и всесторонне вопросы совершенствования устных и письменных вычислений учащихся исследовались лишь в 60-70 гг. ХХ века. Исследования последующих лет посвящены преимущественно разработке качеств вычислительных навыков (М.А. Бантова), рационализации вычислительных приемов (М.И. Моро, С.В. Степанова и др.), применению средств технических средств обучения (В.И. Кузнецов). Каждое из этих исследований внесло определенный вклад в разработку и совершенствование той методической системы, которая использовалась в практике обучения, и нашло отражение в учебниках математики (М.И. Моро, М.А. Бантова, Г.В. Бельтюкова, А.М. Пышкало, С.В. Степанова, Ю.М. Колягин). Действующие на сегодняшний день программы по математике обеспечивают достаточный уровень формирования вычислительных навыков школьников. Изучение вычислительного приема происходит после того, как школьники усвоят его теоретическую основу (определения арифметических действий, свойства действий и следствия, вытекающие из них). Причем в каждом конкретном случае учащиеся осознают сам факт использования соответствующих теоретических положений, лежащих в основе вычислительного приема, конструируют различные приемы для одного случая вычислений, используя различные теоретические положения. В начальном курсе математики предусмотрен такой порядок введения вычислительных приемов, при котором постепенно вводятся приемы, включающие большее число операций, а приемы, усвоенные ранее, включаются в новые в качестве основных операций. Переориентация методической системы на приоритет развивающей функции по отношению к образовательной, характеризующейся изменением характера деятельности учащихся, личностно-ориентированным подходом к обучению, несколько ослабила внимание к развитию и закреплению вычислительных навыков у учащихся. Анализ учебников математики для начальной школы (И.И. Аргинская, Л.Г., Э.И. Александрова, В.В. Давыдов, и др.) в исследовании Н. Б. Истоминой позволил ей сделать вывод, что «все они в той или иной степени способствуют развитию познавательной активности учащихся, их творческого потенциала, развитию гибкости и критичности мышления. Однако задача формирования прочных и осознанных вычислительных умений и навыков отодвинута в них на второй план. Способы организации вычислительной деятельности по-прежнему ориентированы на показ образца вычислительного приема, отработку частных способов вычислений, использование тренировочных упражнений репродуктивного характера». [9] Н. Б. Истоминой отмечается ухудшение качества вычислений учащихся, обучающихся по развивающим учебникам. Особенно пострадала культура устного счета. «Стремление учителей изменить ситуацию приводит к тому, что одни учителя используют в работе два учебника: один выполняет развивающие функции, другой (традиционный) — нацелен на формирование вычислительных умений и навыков. Другие учителя увеличивают объем домашних заданий. Это приводит к перегрузкам школьников, провоцирует стрессовые ситуации, ..., снижает интерес к математике». [9] Многие учителя, признавая устаревшим навык устного счета, не включают его в структуру урока, в результате чего отмечается снижение уровня сложности выполняемых учащимися вычислений. Из исследований прошлых лет наибольшим авторитетом пользуются работы М.А. Бантовой. Обратимся к ее статье «Система формирования вычислительных навыков», опубликованной дважды в журнале «Начальная школа» (№10, 1975 и №11, 1993) [2 ] М.А. Бантова определила вычислительный навык как высокую степень овладения вычислительными приемами. «Приобрести вычислительные навыки — значит, для каждого случая знать, какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия, и выполнять эти операции достаточно быстро». [2] О сформированности любого умственного действия можно говорить лишь тогда, когда ученик сам, без вмешательства со стороны, выполняет все операции, приводящие к решению. М.А. Бантова выделяет следующие характеристики полноценного вычислительного навыка: правильность, осознанность, рациональность, обобщенность, автоматизм и прочность. [2] Однако, сегодня, в век развития электронных средств вычислительной техники, значительно изменивший процесс вычислений, важно создать модель вычислительной культуры, необходимой современному человеку, в частности выпускнику начальной школы, с учетом многообразия типов учебных заведений, профилизации образования. Умение пользоваться микрокалькулятором стало неотъемлемой частью математической культуры современного человека. Поэтому необходимо определиться, какими характеристиками должны обладать вычислительные навыки. Конкретные числа и действия машине задает человек. В некоторых ситуациях машина может дать «сбой», либо задающий ей числа и операции допускает ошибку. Поэтому школьников надо учить давать предварительную оценку результата на основании округления исходных данных и промежуточных результатов действий, т.е. выполнять прикидку (числа цифр результата, его последней цифры с помощью предварительного округления; на основании зависимости между результатами и компонентами арифметических действий; по алгоритму выполнения действий). Следовательно, одной из характеристик вычислительных навыков, наряду с перечисленными выше, выступает умение прогнозировать результат и оценивать его истинность, которое необходимо в дальнейшем обучении. М.А. Бантова под рациональностью вычислений понимает выбор тех вычислительных операций из возможных, «выполнение которых легче других и быстрее приводит к результату арифметического действия».[2] Но рациональный вычислительный прием для одного ученика не всегда рационален для другого. Поэтому, рациональность вычислительного навыка можно заменить его эффективностью. По мнению педагогов, вычислительный навык можно считать эффективным, если в рамках данного способа вычислений получение правильного результата достигается минимизацией затрат умственных ресурсов. Т.е. ученик, используя различные знания, может выбрать не обязательно более рациональный вычислительный прием с точки зрения методики, а более удобный (легкий) для него в конкретной ситуации, быстрее других приводящий к результату. Формирование вычислительных умений и навыков — сложный длительный процесс, эффективность которого во многом зависит от индивидуальных особенностей ребенка, уровня его подготовки и способов организации вычислительной деятельности. На современном этапе развития начального образования необходимо выбирать такие способы организации вычислительной деятельности младших школьников, которые способствуют не только формированию прочных осознанных вычислительных умений и навыков, но и всестороннему развитию личности ребенка. При выборе способов организации вычислительной деятельности учителю необходимо отдавать предпочтение обучающим заданиям, в которых доминирует познавательная мотивация, ориентироваться на развивающий характер работы, учитывать индивидуальные особенности ребенка, его жизненный опыт, особенности детского мышления. Вычислительные задания должны характеризоваться вариативностью формулировок, неоднозначностью решений, выявлением разнообразных закономерностей и зависимостей, использованием различных моделей (предметных, графических, символических). На сегодняшний день, работая в любой системе обучения, учитель может и должен организовать работу по формированию вычислительных умений и навыков у учащихся таким образом, чтобы удовлетворить всем выше перечисленным требованиям современной школы. 2.2 Система формирования вычислительных навыков младших школьников Формирование у школьников 1-IV классов вычислительных навыков остается одной из главных задач начального обучения математике, поскольку вычислительные навыки необходимы как в практической жизни каждого человека, так и в учении. Центральными темами в начальном курсе математики являются нумерация целых неотрицательных чисел и действий над ними. Этот материал изучается по концентрам. Всего выделяются четыре концентра: десяток, сотня, тысяча, многозначные числа. В каждый следующий концентр включаются новые вопросы, и наряду с этим получают развитие вопросы, раскрытые в предыдущих концентрах. Десяток. Выделение темы «Десяток» в особый концентр объясняется рядом причин. Нумерация и арифметические действия в пределах десяти имеют некоторые особенности. Десять – основание десятичной системы счисления, поэтому числа от одного до десяти образуются в результате счета простых единицбез использования других разрядных единиц. Для обозначения каждого из чисел первого десятка применяется в устной речи особое слово, а на письме – особый знак. Арифметические действия (сложение вычитание) непосредственно связаны с операциями над множествами. Случаи служения и вычитания в пределах десяти являются табличными. Они заучиваются наизусть. В теме «Десяток» начинается изучение многих вопросов, работа над которыми продолжается в последующих концентрах. Так, счет в пределах десяти – основа овладения счетом вообще, потому что другие разрядные единицы (десятки, сотни и т.д.) считают точно также, как и простые единицы. Названия и обозначения чисел первого десятка служат исходными для называния и обозначения любых многозначных чисел. Сложение и вычитание в пределах десяти составляют основу выполнения устных и письменных вычислений за пределами первого десятка. Сотня Нумерация чисел в пределах ста и четыре арифметических действий над ними выделяются в особый концентр по следующим причинам. Здесь учащиеся знакомятся с новой счетной единицей – десятком и сложнейшим понятием десятичной системы исчисления – понятием разряда. Усвоение принципов образования, называния, и записи двузначных чисел – основа для усвоения устной и письменной нумерации числе за пределами сотни. Изучая арифметические действия над числами в пределах ста, учащиеся овладевают основными приемами устных вычислений и одновременно усваивают лежащие в их основе свойства действий, связи между результатами и компонентами. Таким образом, это важная ступень в формировании у детей знаний об арифметических действиях и вычислительных навыков. Здесь учащиеся усваивают наизусть таблицу сложения и таблицу умножения (запоминают результаты действий над однозначными числами). Знание этих таблиц дает возможность быстро выполнять и соответствующие случаи обратных действий – вычитания и деления. Прочное усвоение таблиц сложения и умножения – это база для овладения в дальнейшем не только устными, но и письменными вычислениями с многозначными числами. В концентре «Сотня» изучаются следующие вопросы: нумерация чисел, сложение и вычитание, умножение и деление. Тысяча Нумерация чисел в пределах 1000 и арифметические действия над ними выделяются в особый концентр по следующим причинам. Здесь заканчивается изучение нумерации чисел первого класса – класса единиц, что является основой для усвоения нумерации многозначных чисел, так как следующие классы: второй класс – класс тысяч, третий класс – класс миллионов и т. д. строятся по аналогии с первым классом. Поэтому устная и письменная нумерация трехзначных чисел должна быть прочно и осознанно усвоена детьми. В концентре «Тысяча» закрепляются знания устных приемов вычислений. Как и раньше, приемы вычислений раскрываются с опорой на теорию арифметических действий (свойства, взаимосвязь прямых и обратных действий). Это дает возможность учащимся не только самостоятельно объяснять раннее изученные приемы вычислений, применяемые теперь к трехзначным числам, но и «открывать» новые вычислительные приемы. В этом концентре начинается работа над письменными приемами сложения и вычитания, поскольку здесь можно рассмотреть важнейшие случаи и раскрыть письменные приемы этих действий, а также показать преимущества письменных приемов над устными при вычислениях с многозначными числами. Многозначные числа Нумерация многозначных чисел и действия над ними выделяются в особый концентр потому, что нумерация чисел за пределами 1000 имеет свои особенности: многозначные числа образуются, называются, записываются с опорой не только на понятия разряды, но и на понятия классы. Арифметические действия над многозначными числами выполняются с использованием как устных, так и письменных приемов вычислений. Выработка осознанных и прочных навыков письменных вычислений – одна из основных задач изучения действий над многозначными числами. Рассмотрим основные положения системы формирования вычислительных навыков, суть вычислительного приема и вычислительного навыка, характеристику сформированного вычислительного навыка, а также методику работы по формированию вычислительных навыков. Установим, прежде всего, что такое прием вычисления (вычислительный прием). Пусть надо сложить числа 8 и 6. По принятой в настоящее время методической системе прием вычисления для этого случая будет состоять из ряда операций: 1) замена числа 6 суммой удобных слагаемых 2 и 4 2) прибавление к числу 8 слагаемого 2; 3) прибавление к полученному результату, к 10, слагаемого 4. Здесь выбор операций и порядок их выполнения определяется соответствующей теоретической основой приема — применением свойства прибавления к числу суммы (сочетательное свойство):замена числа 6 суммой удобных слагаемых, затем прибавление к числу 8 последовательно каждого слагаемого. Кроме того, здесь используются и другие знания, например, при выполнении первой операции используется знание состава чисел первого десятка: 10=8+2 и 6=2+4. Таким образом, можно сказать, что п р и е м вычисления над данными числами складывается из ряда последовательных операций (системы операций), выполнение которых приводит к нахождению результата требуемого арифметического действия над этими числами; причем выбор операций в каждом приеме определяется теми теоретическими положениями, кот9рые используются в качестве его теоретической основы. В большинстве случаев уже в начальных классах школы для нахождения результата арифметического действия можно использовать в качестве теоретической основы различные теоретическле положения, что приводит к разным приемам вычислений (разным способам вычислений). Например: 1) 15х6=15+15+15+15+15+15=90 2) 15х6=(IО+5)х6=10х6+5х6=90 3) 15х6=I5х(2х3)=(15х2)хЗ=9О Теоретической основой для выбора операций, составляющих первый из приведенных приемов, является конкретный смысл действия умножения; теоретической основой второго приема — свойство умножения суммы на число, а третьего приема — свойство умножения числа на произведение. Операции, составляющие прием вычисления, имеют разный характер. Многие из них сами являются арифметическими действиями. Эти операции играют особую роль в процессе овладения вычислительными приемами: выполнение приема в свернутом плане сводится к выделению и выполнению именно операций, являющихся арифметическими действиями. Поэтому операции, являющиеся арифметическими действиями, можно назвать осно вными. Например, для случая 16х4 основными будут операции: 10х4=40, 6х4=24, 40+24=64. Все другие операции (замена числа суммой, произведением и т. п.) — вспомогательные, хотя в приеме они все одинаково важны. Число операций, составляющих прием, определяется прежде всего выбором теоретической основы вычислительного приема. Например, при сложении чисел 57 и 25 в качестве теоретической основы может выступать свойство прибавления суммы к числу, тогда прием будет включать три операции: замена числа 25 суммой разрядных слагаемых 20 и 5, прибавление к числу 57 слагаемого 20 ; прибавление к результату, к 77, слагаемого 5; Если же теоретической основой явится свойство прибавления суммы к сумме, то прием для того же случая будет включать пять операций: замена числа 57 суммой разрядных слагаемых 50 и 7, замена числа 25 суммой разрядных слагаемых 20 и 5, сложение чисел 50 и 20, сложение чисел 7 и 5, сложение полученных результатов 70 и 12. Число операций зависит также от чисел, над которыми выполняются арифметические действия. Так, при использовании одной и той же теоретической основы — свойства прибавления суммы к сумме — прием сложения чисел 57 и 25 содержит меньше операций, чем прием сложения чисел 257 и 425. Число операций, выполняемых при нахождении результата арифметического действия, может сокращаться по мере овладения приемом. Например, для случаев вида 8+2 на начальной стадии формирования навыка ученик выполняет три операции: замена числа 2 суммой чисел 1 и 1 (хотя в явном виде эта операция не дается), прибавление числа 1 к 8, прибавление числа 1 к результату, к 9; однако после заучивания таблицы сложения ученик выполняет одну операцию — он сразу связывает числа 8 и 2 с числом 10. Как видим, здесь один прием как бы перерастает в другой. Дадим теперь характеристику вычислительного навыка. Вычислительный навык — это высокая степень овладения вычислительными приемами. Приобрести вычислительные навыки — значит для каждого случая знать, какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия, и выполнять эти операции достаточно быстро. Полноценный вычислительный навык характеризуется правильностью. осознанностью, рациональностью, обобщенностью, автоматизмом и прочностью. Правильность — ученик правильно находит результат арифметического действия над данными числами, т. е. правильно выбирает и выполняет операции, составляющие прием. Осознанность — ученик осознает, на основе каких знаний выбраны операции и установлен порядок их выполнения. Это для ученика своего рода доказательство правильности выбора системы операций. Осознанность проявляется в том, что ученик в любой момент может объяснить, как он решал пример и почему можно так решать. Это, конечно, не значит, что ученик всегда должен объяснять решение каждого примера. В процессе овладения навыком объяснение должно постепенно свертываться. Рациональность — ученик, сообразуясь с конкретными условиями, выбирает для данного случая более рациональный прием, т. е. выбирает те из возможных операций, выполнение которых легче других и быстрее приводит к результату арифметического действия. Разумеется, что это качество навыка может проявляться тогда, когда для данного случая существуют различные приемы нахождения результата, и ученик, используя различные знания, может сконструировать несколько приемов и выбрать более рациональный. Как видим, рациональность непосредственно связана с осознанностью навыка. Обобщенность — ученик может применить прием вычисления к большему числу случаев, т. е. он способен перенести прием вычисления на новые случаи. Обобщенность так же, как и рациональность, теснейшим образом связана с осознанностью вычислительного навыка, поскольку общим для различных случаев вычисления будет прием, основа которого — одни и те же теоретические положения. Автоматизм (свернутость) — ученик выделяет и выполняет операции быстро и в свернутом виде, но всегда может вернуться к объяснению выбора системы операций. Программа предусматривает разную степень автоматизации различных случаев выполнения арифметических действий. Высокая степень автоматизации должна быть достигнута по отношению к табличным случаям (5+3, 8—5, 9+6, 15—9, 7Х6, 42:6). Здесь должен быть достигнут уровень, характеризующийся тем, что ученик сразу же соотносит с двумя данными числами третье число, которое является результатом арифметического действия, не выполняя отдельных операций. По отношению к другим случаям арифметических действий происходит частичная автоматизация вычислительных навыков: ученик предельно быстро выделяет и выполняет систему операций, не объясняя, почему выбрал эти операции и как выполнял каждую из них. В этом смысле и говорят об автоматизации вычислительных навыков. Заметим, что осознанность и автоматизм вычислительных навыков не являются противоречивыми качествами. Они всегда выступают в единстве: при свернутом выполнении операций осознанность сохраняется, но обоснование выбора системы операций происходит свернуто в плане внутренней речи. Благодаря этому ученик может в любой момент дать развернутое обоснование выбора системы операций. Прочность — ученик сохраняет сформированные вычислительные навыки на длительное время. Рассмотрим методику формирования вычислительных навыков. Формирование вычислительных навыков, обладающих названными качествами, обеспечивается построением начального курса математики и использованием соответствующих методических приемов. В целях формирования осознанных, обобщенных и рациональных навыков начальный курс математики строится так, что изучение вычислительного приема происходит после того, как учащиеся усвоят материал, являющийся теоретической основой этого вычислительного приема. Например, сначала ученики усваивают свойство умножения суммы на число, а затем это свойство становится теоретической основой приема внетабличного умножения. Так, при умножении 15 на 6 выполняется следующая система операций, составляющая вычислительный прием: 1) число 15 заменяем суммой разрядных слагаемых 10 и 5; 2) умножаем на 6 слагаемое 10, получится 60; 3) умножаем на 6 слагаемое 5, получится 30 4) складываем полученные произведения 60 и 30, получится 90. Как видим, здесь применение свойства умножения суммы на число (термин распределительный закон в начальном курсе не вводится) определило выбор всех операций, поэтому и говорят, что прием внетабличного умножения основан на свойстве умножения суммы на число или что свойство умножения суммы на число — теоретическая основа приема внетабличного умножения. Легко заметить, что кроме свойства умножения суммы на число здесь использованы и другие знания, а также ранее сформированные вычислительные навыки: знание десятичного состава чисел (замена числа суммой разрядных слагаемых), навыки табличного умножения и умножения числа 10 на однозначные числа, навыки сложения двузначных чисел. Однако выбор именно этих знаний и навыков диктуется применением свойства умножения суммы на число. Общеизвестно, что теоретической основой вычислительных приемов служат определения арифметических действий, свойства действий и следствия, вытекающие из них. Имея это в виду и принимая во внимание методический аспект, можно выделить группы приемов в соответствии с их общей теоретической основой, предусмотренной действующей программой по математике для начальных классов, что даст возможность использовать общие подходы в методике формирования соответствующих навыков. Назовем эти группы приемов. 1. Приемы, теоретическая основа которых — конкретный смысл арифметических действий. К ним относятся: приемы сложения и вычитания чисел в пределах 10 для случаев вида а-2, а+2, а-4,а+4;а-0,а+0; приемы табличного сложения и вычитания с переходом через десяток в пределах 20; прием нахождения табличных результатов умножения, прием нахождения табличных результатов деления (только на начальной стадии) и деления с остатком, прием умножения единицы и нуля. Это первые приемы вычислений, которые вводятся сразу после ознакомления учащихся с конкретным смыслом арифметических действий. Они, собственно, и дают возможность усвоить конкретный смысл арифметических действий, поскольку требуют применения конкретного смысла. Вместе с тем эти первые приемы готовят учащихся к усвоению свойств арифметических действий. Таким образом, хотя в основе некоторых из названных приемов и лежат свойства арифметических действий (так, прибавление двух по единице выполняется на основе использования свойства прибавления суммы к числу), эти свойства учащимся явно не раскрываются. Названные приемы вводятся на основе выполнения операций над множествами. 2. Приемы, теоретической основой которых служат свойства арифметических действий. К этой группе относится большинство вычислительных приемов. Это приемы сложения и вычитания для случаев вида: 2+8, 54-20, 54+20, 27+3, 27-3, 40—6, 45-7, 45+7, 50-23, 50+23, 67-32, 67+32, 74-18, 74+18; аналогичные приемы для случаев сложения и вычитания чисел больших, чем 100, а также приемы письменного сложения и вычитания; приемы умножения и деления для случаев вида 14х5, 5х14, 81:3, 18х40, 180:20, аналогичные приемы умножения и деления для чисел больших 100 и приемы письменного умножения и деления. Общая схема введения этих приемов одинакова: сначала изучаются соответствующие свойства, а затем на их основе вводятся приемы вычислений. 3. Приемы, теоретическая основа которых — связи между компонентами и результатами арифметических действий. К ним относятся приемы для случаев 9-7, 21:3,60:20,54:18, 9:1,0:6. При введении этих приемов сначала рассматриваются в связи между компонентами и результатом соответствующего арифметического действия, затем на этой основе вводится вычислительный прием. 4. Приемы, теоретическая основа которых – изменение результатов арифметических действий в зависимости от изменения одного из компонентов . Это приемы округления при выполнении сложения и вычитания чисел( 46+19, 512-298) и приемы умножения и деления на 5, 25, 50. Введение этих приемов также требует предварительного изучения соответствующих зависимостей. 5. Приемы, теоретическая основа которых — вопросы нумерации чисел. Это приемы для случаев вида а-1, а+1, 10+6, 16—10, 16—б, 57.10, 1200:100; аналогичные приемы для больших чисел. Введение эти приемов предусматривается после изучения соответствующих вопросов нумерации (натуральной последовательности, десятичного состава чисел, позиционного принципа записи чисел). 6. Приемы, теоретическая основа которых — правила. К ним относятся приемы для двух случаев: а х 1, а х 0. Поскольку правила умножения чисел на единицу и нуль есть следствия из определения действия умножения целых неотрицательны чисел, то они просто сообщаются учащимся и в соответствии с ними выполняются вычисления. Целый ряд случаев может быть отнесен не только к указанной группе приемов, но и к другой. Например, случаи вида 46+ 19 можно отнести не только к четвертой группе, но и ко второй. Это зависит от выбора теоретической основы вычислительного приема. Как видим, все вычислительные приемы строятся на той или иной теоретической основе, причем в каждом случае учащиеся осознают сам факт использования соответствующих теоретических положений лежащих в основе вычислительных приемов. Это реальная предпосылка овладения учащимися осознанными вычислительными навыками. Общность подходов к раскрытию вычислительных приемов каждой группы — есть залог овладения учащимися обобщенными вычислительными навыками Возможность использования различных теоретических положений при конструировании различных приемов дня одного случая вычисления (например, для случая сложения 46+ 19) является предпосылок формирования рациональных гибких вычислительных навыков. В принятой сейчас системе изучения арифметических действий предусматривается такой порядок введения приемов, при котором постепенно вводятся приемы, включающие большее число операций, а ранее усвоенные приемы включаются в качества основных операций в новые приемы. Например, при изучении сложения и вычитания в пределах 10, сначала вводятся приемы для случаев вида а – 1, а+1, после их изучения и выработки соответствующих навыков вводятся приемы для случаев а+2, а-2, которые включают в качестве операций случаи а+1, а-1; затем вводятся приемы для случаев а -3,а+3, включающие в качестве операций случаи а+2, а-2 и т. д. Как видим, выполняя операции, составляющие новый прием, ученик не только усваивает этот прием, но и совершенствует навыки вычислений ранее рассмотренных случаев. Такая система включения приемов создает благоприятные условия для выработки у учащихся прочных и автоматизированных навыков. Рассмотрим это подробнее в следующей главе. 2.3 Методика работы по формированию вычислительных навыков на уроках математики В методике работы над каждым отдельным приемом можно предусмотреть ряд этапов 1. Подготовка к введению нового приема На этом этапе создается готовность к усвоению вычислительного приема, а именно: учащиеся должны усвоить те теоретические положения, на которых основывается вычислительный прием, а также овладеть каждой операцией, составляющей прием. Следовательно, чтобы обеспечить соответствующую подготовку к введению приема, надо проанализировать прием и установить, какими знаниями должен овладеть ученик и какие вычислительные навыки он должен уже приобрести. Например, можно считать, что ученики подготовлены к восприятию вычислительного приема для случаев а+2, а-2, если они ознакомлены с конкретным смыслом действий сложения и вычитания, знают состав числа 2 и овладели вычислительными навыками сложения и вычитания для случаев вида а-1, а+1; готовностью к введению приема внетабличного умножения (14х5) будет: знание учащимися правила умножения суммы на число, знание десятичного состава чисел в пределах 100 и овладение навыками табличного умножения, навыками умножения числа 10 на однозначные числа, навыками сложения двузначных чисел. Центральное же звено при подготовке к введению нового приема — овладение учеником основными операциями, которые войдут в новый прием. 2. Ознакомление с вычислительным приемом На этом этапе ученики усваивают суть приема: какие операции надо выполнять, в каком порядке и почему именно так можно найти результат арифметического действия. При введении большинства вычислительных приемов целесообразно использовать наглядность. Для приемов первой группы это — оперирование множествами. Например, прибавляя к 7 число 2, придвигаем к 7 квадратам (кружкам и т. п.) 2 квадрата (кружка и т. п.) по одному. При ознакомлении с приемами второй группы в качестве наглядности используется развернутая запись всех операций, что весьма положительно влияет на усвоение приема. Например, при введении приема внетабличного умножения выполняется такая запись: 14х5=(10+4)х5=10х5+45=70. В ряде случаев наряду с развернутой записью используется и оперирование множествами (например, при ознакомлении с приемами сложения и вычитания в пределах 100). Выполнение каждой операции важно сопровождать пояснениями вслух. Сначала эти пояснения выполняются под руководством учителя, а затем учащиеся выполняют их самостоятельно. В пояснении указывается, какие выполняются операции, в каком порядке и называется результат каждой из них, при этом не поясняются ранее изученные приемы, входящие в качестве операций в рассматриваемый прием (основные операций). Например, прибавляя к 7 число 2, ученик так поясняет выполнение операций: к семи прибавлю 1, получится 8; к восьми прибавлю 1, получится 9 (как прибавить 1, не поясняется); при умножении чисел 14 и 5 пояснение будет следующим: заменю число 14 суммой разрядных слагаемых 10 и 4, получится пример: сумму чисел 10 и 4 умножить на 5; умножим на 5 первое слагаемое — 10, получится 50; умножим на 5 второе слагаемое — 4, получится 20; сложим результаты 50 и 20, получится 70 (здесь не поясняется, как умножить 10 на 5, как умножить 4 на 5 и как сложить 50 и 20). Пояснение выбора и выполнение операций приводит к пониманию сущности каждой операции и всего приема в целом, что в дальнейшем станет основой овладения учащимися осознанными вычислительными навыками. Степень самостоятельности учащихся должна увеличиваться при переходе от приема к приему одной группы. Следует учитывать, что во многих случаях ученики могут самостоятельно найти новый вычислительный прием и выполнить соответствуюшее обоснование. Например, установлено, что все приемы устных вычислений над числами в пределах 1000 учащиеся находят самостоятельно, поскольку эти приемы являются прямым аналогом приемов, изученных в концентре «Сотня (сравнить: 9+7 и 90+70, 8.4 и 80.4 и т. п.). Значительно повышается доля самостоятельности учащихся в открытии новых приемов, если используются предписания — планы (Л. Н. Ланда). Например, при изучении сложения и вычитания в пределах 100 учащимся можно предложить руководствоваться при вычислениях таким планом: заменить одно из чисел суммой удобных слагаемых (часто удобными являются разрядные слагаемые), назвать, какой получился пример, решить этот пример удобным способом. Умение пользоваться таким планом приводит к тому, что ученики сами находят различные вычислительные приемы даже для новых случаев, а это есть предпосылка образования рациональных навыков и вместе с тем проявление осознанности и обобщенности вычислительного навыка. З. Закрепление знания приема и выработка вычислительного навыка На этом этапе учащиеся должны твердо усвоить систему операций, составляющих прием, и предельно быстро выполнять эти операции, т. е. овладеть вычислительным навыком. В процессе работы здесь важно предусмотреть ряд стадий в формировании у учащихся вычислительных навыков. На первой стадии закрепляется знание приема: учащиеся самостоятельно выполняют все операции, составляющие прием, комментируя выполнение каждой из них вслух и одновременно производи развернутую запись, если она была предусмотрена на предыдущем этапе. Таким образом, здесь учащиеся выполняют самостоятельно то же, что на предыдущем этапе выполняли под руководством учителя. Подробное объяснение и развернутая запись позволяют им осознанно усвоить вычислительный прием. Начинается эта стадия, как правило, на том же уроке, на котором учитель знакомит детей с новым приемом. Заметим, что не следует слишком долго задерживать учащихся на этой стадии, иначе они настолько привыкают к подробной записи и подробному объяснению, что всегда пользуются ими, а это тормозит свертывание выполнения операций. На второй стадии происходит частичное свертывание выполнения операций: учащиеся про себя выделяют операции и обосновывают выбор и порядок их выполнения, вслух же они проговаривают выполнение основных операций, т. е. промежуточных вычислений. Надо специально учить детей выделять основные операции в каждом вычислительном приеме. Так, при формировании навыка внетабличного умножения учитель на этой стадии указывает, чтобы при умножении, например, 27 на З ученики про себя заменили число 27 суммой разрядных слагаемых (20 и 7), про себя сказали, какой получился пример (сумму чисел 20 и 7 умножить на 3), а вслух объяснили, как удобнее решить этот пример, называя только, над какими числами и какие арифметические действия они выполняют (20 умножить на 3, получится 60; 7 умножить на 3, получится 21; к 60 прибавить 21, получится 81). Развернутая запись при этом не выполняется. Сначала такое проговаривание ведется под руководством учителя, а затем самостоятельно. Проговаривание вслух помогает выделить и подчеркнуть основные операции, а выполнение про себя вспомогательных операций способствует их свертыванию, т. е. быстрому выполнению в плане внутренней речи. На третьей стадии происходит полное свертывание выполнения операций: учащиеся про себя выделяют и выполняют все операции, т. е. здесь происходит свертывание и основных операций. Чтобы добиться этого, надо и на этой стадии руководить деятельностью учащихся: учитель предлагает детям выполнять про себя и промежуточные вычисления (основные операции), а называть или записывать только окончательный результат. На этой стадии свертывание основных операций будет несколько отставать от свертывания вспомогательных операций (их свертывание началось на предыдущей стадии), благодаря чему основные операции будут актуализироваться, т. е. ученики воспроизведут именно те операции, выполнение которых позволит им правильно и быстро найти результат арифметического действия. Актуализация основных операций и выполнение их в свернутом плане и есть собственно вычислительный навык.

На четвертой стадии наступает предельное свертывание выполнения операций. Программы по математике включают большой интересный материал по проблеме формирования прочных навыков вычислений, однако, по-прежнему некоторые вопросы понимания и отработки навыка арифметических вычислений являются для младших школьников довольно сложными.

На всех стадиях формирования вычислительного навыка решающую роль играют упражнения на применение вычислительных приемов, причем содержание упражнений должно подчиняться целям, которые ставятся на соответствующих стадиях. Важно, чтобы было достаточное число упражнений, чтобы они были разнообразными как по числовым данным, так и по форме, чтобы при этом предусматривались аналогии в приемах и в соответствии с ними предлагались упражнения на сравнение приемов, сходных в том или ином отношении. Названные стадии не имеют четких границ: одна постепенно переходит в другую. Надо иметь в виду, что свертывание выполнения операций не у всех учащихся происходит одновременно, поэтому важно время от времени возвращаться к полному объяснению и развернутой записи приема. Продолжительность каждой стадии определяется сложностью приема, подготовленностью учащихся и целями, которые ставятся на каждой стадии. Существенное влияние на формирование письменных вычислительных навыков оказывает качество записей арифметических действий, промежуточных и окончательных результатов. Поэтому утащимся необходимо владеть следующими навыками: - отчетливо писать математические символы (цифры, знаки арифметических действий); - цифры и знаки располагать строго в соответствии с правилами арифметических действий; - безошибочно применять таблицы сложения и умножения натуральных чисел; - овладение техникой устного счета. Правила приема вычислений не зависит от того, выполняются они письменно или устно. Однако, владение навыками устных вычислений представляет большую ценность, так как они ускоряют письменные вычисления, позволяют усовершенствовать их. Таким образом, правильное выделение стадий формирования вычислительных навыков позволит учителю управлять процессом усвоения учащимися вычислительного приема, постепенного свертывания выполнения операций, образования вычислительных навыков. Обучение письменным приемам вычисления Обучение математике в начальной школе осуществляется по различным образовательным системам (системы М. И. Маро, И. А. Бантовой, Г. В. Бильтюковой, система общего развития школьника Л. В. Занкова, система «Гармония» Н. Б. Истоминой, система развивающего обучения Д. Б. Эльконина-В.В.Давыдова, «школа 2100»…). В нашей работе мы рассмотрим формирование вычислительных навыков по системе «Гармония» .

Глава 3. Опытно-экспериментальное изучение использования дидактической игры как средства формирования вычислительных навыков учащихся начальных классов

3.1 Изучение сформированности вычислительных навыков учащихся начальных классов

Как мы выяснили в теоретической части нашей работы, правильное выделение стадий формирования вычислительных навыков позволит учителю управлять процессом усвоения учащимися вычислительного приема, постепенного свертывания выполнения операций, образования вычислительных навыков.

База исследования: шк. № 2, Домбаровского района, 3 класс.

В общеобразовательной школе в 3 классе нами была запланирована и проведена экспериментальная работа, состоящая из трех этапов: констатирующего, формирующего и контрольного. Экспериментальная работа была проведена с целью формирования вычислительных навыков у детей младшего школьного возраста.

В третьем классе по программе «Гармония» изучаются следующие темы, в которых формируются вычислительные навыки:

- сочетательные и распределительные свойства умножения;

- деление любого числа на единицу, само на себя, деление 0 на число;

- деление «круглых» десятков на 10 и на «круглые « десятки;

- табличные случаи умножения и деления;

- умножение и деление двузначных чисел на однозначные;

- деление двузначных чисел на двузначные;

- нумерация, сравнение, сложение и вычитание многозначных чисел (4-ех, 5-ти, 6-ти значные).

В тесной связи с ними рассматривается и весь другой материал:

- площадь и периметр прямоугольника;

- цена, количество, стоимость;

-единицы массы и времени;

- решение различных задач.

Наша опытно-экспериментальная работа проводилась в 4 четверти в 3 классе по теме «Сложение и вычитание многозначных чисел». На данную тему программой предусмотрено восемь уроков. Два урока отводится на сложение многозначных чисел (знакомство с правилом письменного сложения без перехода через разряд и с правилом письменного сложения с переходом) и отработку навыков письменного сложения многозначных чисел. Два урока на вычитание многозначных чисел (знакомство с различными видами вычитания многозначных чисел, с правилом записи, отработка навыков вычитания).

Для выявления степенью владения младшими школьниками вычислительных навыков нами был проведен констатирующий эксперимент.

Констатирующий эксперимент

Цель: на основе диагностического исследования выявить сформированность вычислительных навыков.

С этой келью в экспериментальном классе мы провели проверочную работу:

1 вариант: П вариант

12333 + 21439 = 43900 + 99899 =

143799 + 131466 = 33772 + 10128 =

34587 - 12498 = 74532 – 21456 =

9897045 – 34690 = 479089 – 34521 =

Узнайте, насколько больше

806003, чем 70873 907005, чем 70975

Уровень сформированности вычислительных навыков мы оценивали по следующим критериям:

Оптимальный – оценка «5»

Допустимый – оценка «4»

Недопустимый – оценка «3»

Мы получили следующие результаты:

На 5 написали – 3 человек

На 4 написали 5 человека

На 3 написали 6 человек

На 2 написал 1 человека

Таким образом, уровень сформированности вычислительных навыков можно представить в следующей таблице:

Табл. 1

Уровни сформированности вычислительных навыков младших школьников

КЛАСС	Уровни сформированности вычислительных навыков младших школьников, %
	оптимальный	допустимый	недопустимый
3 кл. 15 чел.	20%	73, 3%	6, 7%

Представим результаты для большей наглядности в следующем графике:

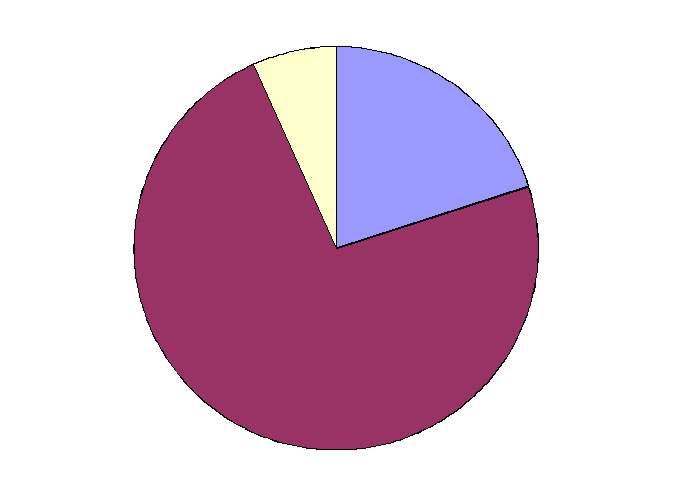
Рис. 1 Уровень сформированности вычислительный навыков у учащихся 3 класса на стадии констатирующего эксперимента

Оптимальный уровень

Допустимый уровень

Недопустимый уровень

Таким образом, недопустимый уровень вычислительных навыков составляет 6, 7 %.

Для формирования вычислительных навыков мы провели формирующий эксперимент.

3.2 Использование дидактической игры как средства формирования вычислительных навыков учащихся начальных классов

Цель формирующего эксперимента – сформировать вычислительные навыки у учащихся 3 класса используя дидактические игры.

Урок 1. Сложение и вычитание многозначных чисел

Цель: отработать навыки сложения и вычитания многозначных чисел.

Ход урока:

I. Организация класса.

П Устный счет.

На доске таблица:

х	6	5	4	7	9
900 8000 70000

(5 человек работают у доски)

Остальные выполняют самостоятельно.

Ш. Постановка темы урока. Отработка навыка сложения и вычитания многозначных чисел.

Дидактическая игра «Клоуны»

Цель: формировать вычислительные навыки у учащихся.

- Ребята, к нам пришли клоуны, которые разучились считать, забыли чем они отличаются друг от друга одни записи от других. Давайте поможем им? Ответьте:

– Чем похожи и чем отличаются записи?

38456 38453

12345 12345

Найдите значения выражений (стр. 158, № 520)

2459+121 53075+2306

2458 + 122 53076+2305

2457+123 53006+2375

2456 + 124 53306 + 2075

- А вот и не правильно! Закричали клоуны.

- Давайте докажем, что мы правильно посчитали?

Проверьте себя, выполнив сложение в столбик.

Можно ли утверждать, что значения суммы в каждом столбике одинаковы?

Давайте проверим

2459 2458 2457 2456

121 122 123 124

2580 2580 2580 2580

53075 53076 53006 53306

2306 2305 2375 2075

55381 55381 55381 55381

Физкультпауза.

VI Отработка устного счета (№ 523, стр. 159 учеб.)

Найди значение выражений:

(30034 + 570080) х 0 + 0 х 89090

209009 х 0 + 900320 х 1

38007 х 1 – 303003 х 0

Не вычисляя, найдите значения выражений

(30034 + 570080) х 0 + 0 х 89090 = 0

209009 х 0 + 900320 х 1 = 900320

38007 х 0 + 270008 = 270008

803370 х 1 – 303003 х 0 = 803370

V Итог урока.

VI Домашнее задание: № 106, 107.

Урок 2. Сложение и вычитание многозначных чисел.

Цель: отработать навыки устного и письменного сложения и вычитания многозначных чисел.

Ход урока:

I Организация класса

П Устный счет

На доске запись:

101010 – 2020

202020 – 3030

303030 – 4040

404040 – 5050

Разгадайте правило составления выражений и найдите их значения

101010 202020 303030 404040

2020 3030 4040 5050

98990 198990 298990 398990 и т.д.

Ш Постановка темы урока

Мы продолжаем совершенствовать свои навыки в сложении и вычитании многозначных чисел.

Игра «Сказочная география».

Дидактическая цель: формировать вычислительные навыки.

На доске карта сказочной страны.

а) – Перед вами цифры, с помощью которых необходимо записать четыре шестизначных числа: 1, 0, 3, 4, 2. 1. Их было несколько, но остальные стерлись. Давайте, восстановим цифры. Эти цифры означают, сколько деревьев в лесу, сколько звезд на небе, сколько рек, ручейков и маленьких озер в этой сказочной стране.

( 103103, 331100, 301100, 310310 и т.д.)

( 421421, 442211, 412412, 124124 и т. д. )

Составьте из этих чисел различные суммы, найдите их значения:

103103 331100 301301 310310

421421 442211 412412 124124

524524 773311 713713 434434

Составьте из этих чисел различные разности и найдите их значение:

421421 442211 412412 310310

103103 331100 124124 318318

111111 111111 186186 186186

Физкультпауза

Спасибо, ребята! Вы очень помогли сказочным географам и астрономам.

IV. Отработка навыков сложения и вычитания многозначных чисел.

а) № 522. Догадайся! Насколько нужно уменьшить 999999, чтобы получить число:

а) 666666;

б) 555555;

в) 444444.

Проверь себя, выполни вычитание в столбик.

999999 – = 666666

999999 – = 44444

999999 – = 5555

999999 999999 9999999

666666 44444 5555

333333 955555 994444

№ 525

Увеличь число 30875 в три раза и догадайся, как найти значение произведения :

30875 х 3 = (30000 + 800 + 70 + 5) х 3 =

30 х 3 + 800 х 3 + 70 х 3 + 5х 3 +

90000 + 2400 + 210 + 15 = 92625

30875

30875

30875

92625

№ 526. Уменьши число 95004 на 4273. Можно ли утверждать, что значение разности будет больше, чем 90000. проверь себя, выполни вычитание в столбик.

95004

4273

90731

V. Итог урока.

VI. Домашнее задание.

Урок 3. Сложение и вычитание многозначных чисел

Цель: отрабатывать навыки сложения и вычитания многозначных чисел, усвоение нумерации чисел, табличных случаев сложения и вычитания в пределах 20.

Ход урока:

I. Организация класса.

П Устный счет.

Догадайся, какими приемами можно заменить каждую букву, чтобы получилась верная запись.

ААААА ААББ

– АББА + БАЕ

АБААБ АГГВ

(Б = 0, А – любое число) (А –любое число, кроме 0

Б –любое число, кроме 0

Г. В. Е. – любые числа

ААББ

+ БАБ

БГГГ

(А = 4,5,6,7,8,9. Б = 5,6,7,8,9. Г = 0, 2,4,6,8)

Ш Постановка темы урока.

Совершенствование навыков сложения и вычитания многозначных чисел.

Можно ли не вычисляя значений выражений, поставить знаки меньше и больше так, чтобы получились верные неравенства:

9999 + 9999 ….. 63003 + 13004

384 + 1987….. 999 + 9998

18007 + 270018 …. 100004 + 180007

6002 – 5999… 6002 – 5999.. 6002 – 5999… 6002 – 5999

80000 – 4444 … 80000 – 9999

Проверь себя, выполнив вычисления в столбик.

№ 533. Запиши пять чисел, в которых 80000. Увеличь каждое на 8739. Вычисли значение сумм в столбик. Как ты можешь проверить результат без калькулятора.

№ 534. Вычисли значение выражения в столбик.

12333 + 21439 34587 – 12498

33772 + 10128 98745 – 3469

43900 + 99899 74532 – 21456

143799 + 131466 479089 – 34521

Узнайте, насколько больше :

807003, чем 70873 | 9070005, чем 70975.

Задание: найди ответ на вопрос, решив математическую цепочку:

V . Итог урока.

VI. Домашнее задание

Урок. 4.

Нахождение значений математических выражений.

К этому виду вычислений можно отнести и числовые выражения и выражения, содержащие переменную. Числовые выражения могут предлагаться в различной словесной формулировке. Например, из 10 вычесть 5; 12 минус 7; уменьшаемое 21 вычитаемое 7, найти разность. Числовые выражения могут включать в себя одно арифметическое действие или несколько действий со скобками и без скобок. Например:

12 + (7 - 4) : 5;

35 – 15:2;

14+15*3.

Числовые выражения могут быть заданы в форме таблицы, окошек, рамок, и т.д. Например, задание заполнить недостающие числа в таблице.

Уменьшаемое	56	95	64	97
Вычитаемое	43	34	24	65
Разность

Математические выражения могут быть заданы в форме выражения, содержащего одну или несколько переменных. Например, такое задание: “Найти значение выражения а + 15 при следующих значениях переменной 5, 10, 15, 20”. Подставляя данные вместо буквы, находят значение выражения. Цель каждого из этих заданий выработать вычислительные навыки.

В этом случае можно применить такие типы дидактических игр как игра «Кто быстрее», когда команды учащихся соревнуются в заполнении таблиц, получая положительные очки за каждое правильное высказывание и отрицательные за каждую ошибку.

Сравнение математических выражений

Можно научить сравнивать числовые выражения и выражения с переменной. Существуют следующие способы сравнения выражений:

• на основе нахождения значения каждого выражения и их сравнения;

• на основе знания свойств арифметических действий;

• на основе знания зависимости изменения результата действия от изменения одного из компонентов;

• на основе знания зависимости изменения результатов результата действия от изменения одного из компонентов;

• на основе знания частных случаев выполнения арифметических действий с числами 1 и 0.

Например, можно предложить найти похожие пары выражений по способу их сравнения.

6 +9 и 9 + 6; 81:9и81:3; 10 : 2 и ( 4+6 ): 2;

10*8 и 8*10; 82 – 1 и 76 + 0, 24 – 8 и 22 – 8,

22+ 7 и 22+ 14; 20*0 и 44*1; 22 + 14 и 22 + (10 + 4 );

После анализа сравнения каждой пары выражений, распределяют их на следующие группы:

1 группа 2 группа 3 группа 4 группа

6 + 9 и 9 + 6 10*8 и 8*10; 22 + 7 и 22 + 14; 20*0и44*1;

22+14 и 22+( 10+4); 81:9и81:3; 82 – 1 и 76 + 0;

10:2и(4+6):2; 24 – 8 и 22 – 8;

Сравнение выражений группы основано на знании свойств арифметических действий. Сравнение выражений 2 группы основано на нахождении значения каждого выражения и их сравнения. Сравнение выражений 3 группы основано на знание зависимости изменения результатов действия от изменения одного из компонентов. Сравнение выражений 4 группы основано на знании частных случаев выполнения арифметических действий с числами 1и 0.

На такой же теоретической основе можно провести сравнение выражений с буквенными значениями. Задание такого вида можно рассматривать как обобщение возможных способов сравнения. Например, нужно сравнить такие пары выражений:

а + в и в + а;

с-8 и с - 1; в+13 и в-13;

16-а и 28-а;

72 : к и 36 : к;

8* а и 18* а;

Решение уравнений

Можно предлагать уравнения в привычном виде. Например: а+12 = 21; в-8 = 17..

Здесь можно провести игру "Принеси ответ". Урок проводится в заранее выбранном учителем месте, где ученики могут собрать разнообразный природный материал (шишки, желуди, каштаны, листья, мелкая галька и т.д.). Ученики разбиваются на несколько команд, каждая из которых получает свое задание на сбор какого-нибудь из возможных природных материалов в соответствии с решением того или иного уравнения. Собранные группы предметов сравниваются, принесшие неверное количество отдают фант или выбывают из игры. (Побочным результатом урока является появление большого количества раздаточного природного материала, который учитель использует в дальнейшей работе на уроках в классе).

     Урок 5.  План-конспект урока математики

Игра “Математическое многоборье”

Цели:

• развитие интереса к математике;

• формирование вычислительных навыков;

• активизация деятельности учителя и учащихся;

• воспитание коллективизма, стремления к творческой деятельности.

Задачи:

• развитие познавательного интереса;

• развитие навыков коллективной работы;

• развитие интереса к решению нестандартных задач и заданий.

Оформление: плакаты с высказываниями великих людей о математике.

Ход урока:

Урок состоит из трех частей:

1 часть – начало. У учащихся формируется психологическая готовность к восприятию – приветствие учителя, представление жюри, объяснение правил игры, приветствие команд.

2 часть – основная. Задания подобраны с учетом пройденного материала. Есть задания и легкие, и повышенной сложности. Это позволит командам получить хотя бы минимальное количество баллов. После каждого этапа объявляется предварительный результат.

3 часть – заключение. Объявление результатов.

Спортивный дух соревнования активизирует возможности детей, что позволит всему мероприятию уложиться в 45 минут.

Учитель: - Добрый день! Я рада приветствовать всех вас на нашем “Математическом многоборье”. В соревнованиях принимают участие две команды – “Знайка” и “Вундеркинд”. Наши соревнования будет судить строгое жюри в составе: …, … .

Ознакомимся с правилами соревнований.

1. Командам быть очень внимательными.

2. Отвечать на вопросы заданий письменно.

3. Ответы на задания приносит капитан команды на стол жюри.

4. Та команда, которая первая принесет правильный ответ, зарабатывает дополнительный балл.

Итак, команды готовы? Начинаем.

Прошу команды поприветствовать друг друга и уважаемое жюри.

Приветствие команд было домашним заданием.

Учитель: - Как и у всех спортсменов, у нас тоже будет разминка. (В качестве разминки предлагается задача на сообразительность).

Задание № 1 – Разминка.

“Стоит в поле дуб. На дубе три яблока. Ехал добрый молодец и сорвал одно яблоко. Сколько яблок осталось?”

Ответ: на дубе яблоки не растут.

Задание № 2 – Стрельба из лука.

Поставьте в клеточки такие числа, чтобы суммы по вертикали, горизонтали и диагонали были равными.

28	20	12
		22

Ответ:

18	16	26
28	20	12
14	24	22

Задание № 3 – Эстафета.

Продолжи числовой ряд ( допишите два числа)

А) 18, 9, 21, 15, ?, ?

Б) 28, 16, 32, 24, ?, ?

Ответ: А) 3, 12

Б) 36, 8

Задание № 4 – Прыжки в высоту.

Расставь знаки и скобки так, чтобы получились верные равенства.

4 4 4 4 = 1 4 4 4 4 = 6

4 4 4 4 = 2 4 4 4 4 = 7

4 4 4 4 = 3 4 4 4 4 = 8

4 4 4 4 = 4 4 4 4 4 = 9

4 4 4 4 = 5 4 4 4 4 = 10

Ответ:

4:4+4-4 = 1 (4+4):4+4 = 6

4:4+4:4 = 2 4+ 4- 4: 4 = 7

(4+4):4+4 = 3 4+4-4+4 = 8

(4-4)·4+4=4 4:4+4+4=9

(4·4+4):4=5 (44-4):4=10

Задание № 4 – Бег на короткие дистанции.

Проверка знания таблицы умножения на 3. Участники называют все числа от 1 до 30, но вместо чисел, делящихся на 3, говорят фразу “Не собьюсь”.

1, 2, не собьюсь, 4, 5, не собьюсь, 7, 8, не собьюсь и т.д.

Задание № 6 – Бег с препятствиями

Решить задачи.

№1. На педсовет собрались 40 строгих учительниц, и все стали по очереди ругать одного печального третьеклассника. Каждая учительница ругала по 12 минут. Сколько часов ругали печального третьеклассника?

Ответ: 8 часов.

№2. 40 бабушек поехали кататься на мотоциклах. Впереди на мотоцикле ехала в одиночестве самая шустрая бабушка, за ней мчались три мотоцикла с колясками, на каждом из которых поместились по три бабушки, а сзади их догоняли остальные мотоциклы. На оставшихся мотоциклах сидело по 2 бабушки. Сколько всего мотоциклов было у бабушек?

Ответ: 19 мотоциклов.

Задание № 7 – Синхронное плавание.

№1. На сколько частей разделится лист бумаги четырьмя прямыми линиями, проходящими через одну точку.

Ответ: 8 частей.

№2. Пирог прямоугольной формы двумя разрезами разделили на 4 части так, что две из них были четырехугольной формы, а две – треугольной.

Задание № 8. – Фехтование ( конкурс капитанов)

Расположить карточки так, чтобы произведение возрастало.

7·8	7·4	9·6	6·6	9·8
Ч	У	А	Д	А

 

7·6	8·3	8·6	8·7	9·6
С	У	П	Х	Е

Ответ:

После решения и расположения карточек с результатами в порядке возрастания должны получиться два слова “УДАЧА” и “УСПЕХ”.

Задание № 9 – Шахматисты.

Задачи на логическое мышление.

№1. Пять человек водили хоровод, держась за руки. В одном месте хоровод расцепился. Сколько рукопожатий осталось в хороводе?

Ответ: четыре.

№2. Великан жил на втором этаже девятиэтажного дома. Как-то ему захотелось жить повыше. Он перевернул дом и поставил его крышей вниз. На каком этаже оказалась его квартира?

Ответ: на восьмом.

Урок 6. Мы применили на уроке дидактическую игру «Ромашка» и другие упражнения, способствующие формированию вычислительных навыков .

Дидактическая игра «Ромашка»

4. Ромашка:

На лепестках цветка написаны числа от 1 до 100, а в середине знак (+, -) (x, : ) и прорезь, куда вставляются числа. Это пособие помогает проводить игру "Молчанка".

В начальных классах важно систематически тренировать учащихся в устном решении примеров.

Можно использовать для этого карточки, покрытые целлофаном:
1. Лабиринт.

2. Лесенка.

На карточках могут быть написаны различные задания, но главное, что прозрачность целлофановой плёнки даёт возможность их использовать несколько раз. Изготовление их занимает меньше времени.
Работа с карточками способствует лучшему усвоению учебного материала, формированию вычислительных навыков, вызывает интерес к учебе.
Формированию осознанных знаний, прочных умений и навыков способствуют самодельные таблицы.

При работе над темой "Сложение и вычитание" с переходом через 10 (в пределах 20) облегчает работу таблица.

Принцип её действия следующий: при сложении (вычитании) чисел прибавляем (вычитаем) столько единиц, чтобы образовался десяток, а затем складываем (вычитаем) оставшиеся единицы.
При изучении темы "Сложение и вычитание" в пределах 100 (без перехода через 10) использую таблицу - опору. Окошечки работают на детей. Дети сами учатся складывать двузначные и однозначные числа и делают выводы. Объясняя, как к 65 прибавить 3, учащиеся сами передвигают на таблице нужную ленту с цифрами и показывают полученное число единиц. То же самое происходит и десятками. Затем при повторении используется нижняя часть таблицы, где стрелками обозначено само объяснение.

При объяснении материала по теме "Порядок действий" помогает также таблица.

-О чем задумался Незнайка и зачем к нему прилетели птички?
(Уставшие и голодные птички должны свить гнездышко. Незнайка задумался, как им помочь. Ему на помощь пришли сами же птички: "Сначала давайте соберем зернышки, поклюем их, а потом, став сильными, полетим за веточками для гнездышка.").

-А как на таблице изображены зернышки и веточки? Какими знаками они обозначены? (поисковая работа).

Незнайка запомнил порядок действий, который ему предложили птички и решил попробовать выполнить примеры на порядок действий.

Разбор примеров

30-2х4=
20:4+9=

-Что сначала предложили птички?

-Как вы будете делать?

На следующем этапе предлагаются примеры в 3-4 действия:

40+21:7-10=
60-4х5+36:6=

Дети сами объясняют порядок действий.

На следующих уроках ввожу примеры со скобками:

70+(4х5+10х2)=
(5х6-12)-3х5=

В помощь детям предлагается другая таблица на порядок действий. Она уже знакома частично. Когда изучали решение примеров на сложение и вычитание без скобок и со скобками. Таблица образно напоминает, что в первую очередь надо выполнять действия в скобках.
Эти таблицы ведут от образных восприятий - к математическим действиям, через осмысление - к практике.

Таким образом, чтобы новый материал эффективно запомнился, необходимо активизировать мыслительную деятельность детей. Важным звеном формирования вычислительных навыков являются дидактические математические игры. Они позволяют быстро изучить и закрепить знания таблицы сложения и вычитания, умножения и деления.

1. "Кто быстрее".

Напротив каждого ряда прикрепляется картинка, под которой записаны примеры.

Самолет	Машина	Катер
7+8 12-5	9+5 13-6	6+7 12-8

2. "Садовники".

На листе бумаги нарисовано дерево - яблоня. К ней прикрепляются яблоки, на обратной стороне которых записаны примеры, К доске выходят ученики, срывают яблоки и решают примеры, Аналогично можно использовать игру "Грибники", "Спрячемся от лисы".
Это часть игры, которые я провожу на уроках математики. Дети любят помогать доктору Айболиту, Краской Шапочке, белочке, составлять букеты для мам.

Игровой момент может включен в середине урока, в конце или в начале, в зависимости от темы и цели урока, характера игры. Иногда можно проводить пятиминутки с разнообразными заданиями.
1). Списать числа, которые делятся на 3

2). Списать числа. Обвести числа, которые делятся на 5 в кружок, а числа, которые делятся на 3 в квадрат

5

21

43

19

25

10

3

12

24

30

За несколько уроков до изучения новой темы включаются в устный счёт задания, подготавливающие к восприятию неизвестного материала. Так за 8 - 10 уроков до изучения темы "Умножение двузначного числа на однозначное во время устного счёта предлагаются задание вида:
1). Представьте числа в виде суммы разрядных слагаемых:

2) Представьте числа в виде разрядных слагаемых и умножьте каждое слагаемое на 2, 3 , 4

Такие задания не только формируют вычислительные навыки, но и развивают устойчивость внимания, увеличивают его объем, учат распределять и переключать его.

На каждом уроке, может только за исключением контрольных работ, всегда найдется место для игры. Она заводит, интригует, мобилизует силы, открывает нераскрытые резервы:

1. Дети с большим интересом и вниманием воспринимают материал. Многие темы начинала в виде игры. Так изучая умножение обыкновенных дробей, учащиеся “получили” письмо от Бабы-Яги с просьбой о помощи: “Сколько надо сока, чтобы разлить его в пять бутылей по ? л каждая?”

2. Соревнуясь в игровой форме, дети быстро вспоминают все, чего не могут вспомнить при обычных ответах, т.е. происходит отработка материала. Например, игра "Крестики-нолики". Задаю теоретические вопросы, дети быстро отвечают на них. Ответ правильный у девочек - плюс, у мальчиков - нуль. Ответы заношу в знакомый всем квадрат. В конце игры суммируем плюсы и минусы. Данную игру можно всячески видоизменять, назначать баллы, объединять детей в команды и т.д.

3. Игра объединяет класс: открываются умение подстраховать друг друга, выслушать каждое мнение. Например, игра "Что? Где? Когда?". Здесь важны не столько знания, сколько умения детей обсуждать вопрос и выслушать позицию другого. У них меняются мнения о своих одноклассниках, при этом меняется и их статус в группе.

4. На основе игры можно выделить ребенка, которому необходима помощь. Всегда есть возможность специально подстроить игру так, чтобы отличился тот учащийся, который больше всего нуждается в поддержке.

5. Во время игры ребенок максимально мобилизован: он сам вычерпывает из себя все свои имеющиеся знания. Например, при изучении новой темы игры на сообразительность, на нестандартное мышление, логику, когда приветствуется каждый ответ, и не беда, что он неверный.

6. Вопрос дисциплины исчезает как бы сам собой: дети погружены в игру так, что отвлечены от всего остального. Правда, если присутствует идея соревнования, то могут быть выкрики “поддержки” своих не очень “умелых” членов команды.

7. После игры дети могут некоторое время монотонно работать, что тоже важно. Поэтому, поиграв с детьми на внимание, можно спокойно и вполне размеренно вести урок. Важно и то, что в игре у ребенка пропадают многие школьные комплексы, связанные с общением, боязнью ответить неправильно, оказаться в одиночестве своих проблем и своего непонимания. Единственное – это, как и в любом деле, необходимо знать меру, “ не заиграться”, т.е. не превращать учебу в нечто поверхностное и игривое.

Игровые действия участников состоят в том, чтобы быстро и без ошибок отвечать на вопросы; выполнять нужные записи; выполнять задания у доски; следить за правильностью ответов своих одноклассников; во время объявленной консультации консультировать соседей по команде или при необходимости самому брать консультацию; не нарушать дисциплину; быть внимательным и активным.

Фрагмент урока с использованием игрового момента на одном этапе.

На доске крепятся три плаката , за которыми “спрятаны” примеры для устного счета.

Учащимся раздаются листы, в которые они фломастером записывают свою фамилию, класс и полученные ответы.

Время выполнения или регламентирует учитель, или происходит ориентация на выполнения задания примерно одной пятой всех учащихся. В последнем случае ученики, выполнившие задание встают со своего места, что тоже является “подстегивающим” стимулом для остальных.

Проверку ответов можно провести несколькими способами:

1) листы сдаются на проверку учителю, при этом каждому выставляется оценочный балл в журнал;

2) учащиеся по просьбе учителя поднимают листы вверх, учителю сразу видно как каждый справился с заданием;

3) учащиеся самостоятельно сравнивают свои ответы с образцом верных ответов (на доске, на листе учителя и т.д.), при этом возможна взаимопроверка в парах.

1. К нам в гости пришла весёлая точка. Одна точка отправилась навестить другую. Каким путём она пойдёт?

 

Ответы детей самые различные. Они доказывают измерением самый короткий путь. Доказывают, что через две точки можно провести только одну прямую.

2. Запишите все двузначные числа до 20. Выпишите только те числа, которые можно представить:

а) в виде суммы одинаковых слагаемых (10,12,14,16,18,20); отметьте закономерность в записи этих чисел ( каждое последующее число на 2 больше предыдущего)

б) в виде суммы трёх одинаковых слагаемых (12,15,18);

Докажите вычислением.

Такие задания заставляют размышлять, пробовать, ошибаться и, наконец, находить правильный ответ. Дети постоянно ищут рациональный способ решения, делают для себя открытия.

При работе с задачей главное - научить детей работать с текстом. Так, например, можно давать задачи с недостающими данными. Например: «Мама принесла домой яблоки, груши и апельсины – всего 10 штук.

Яблок – 4. Сколько мама принесла груш?

-Можно ли этот текст назвать задачей?

-Можно ли найти ответ?

-Почему?

Измените текст так, чтобы можно было найти ответ.

Главное в том, что дети учатся анализировать условие задачи, рассуждать, привыкают отвечать не учителю, а классу, выражая своё мнение: «Я думаю», «Я хочу добавить», «Я не согласен с ним». Умение ставить вопросы, побуждает детей использовать знания в новой ситуации.

Можно урок начинать с устного счёта. Но это должно быть что-то необычное и в тоже время познавательное.

1.Найдите закономерность в двух первых треугольниках. Как связаны между собой числа?

Вместо знаков вопроса впишите везде нужные числа.

 

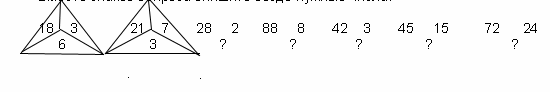
-Какую операцию мы производим с числами?

2. Какое слово зашифровано?

-Как вы понимаете значение этого слова?

А теперь решите устно задачи.

1. В 1984 г. в нашей стране было создано 143 заповедника, за последние десять лет создано ещё пятьдесят новых заповедников.

Сколько заповедников стало в нашей стране?

2. Одно крупное предприятие выбрасывает в атмосферу 200 тонн сажи в год. После установки очистительных сооружений на этом предприятии количество выбросов уменьшилось в двадцать раз. Сколько тонн сажи выбрасывается в атмосферу после установки очистительных сооружений?

3. Из 250 000 видов растений Земли 1/10 часть находится на грани исчезновения. Сколько видов растений на Земле на грани исчезновения?

4. Головоломка «Задумайте любое однозначное число, кроме нуля. Увеличьте число в 100 раз. Результат разделите на задуманное число. Прибавьте к полученному частному 200. У вас получилось 300?

5. Давайте сыграем в игру «Кто быстрее?» Поставьте скобки так, чтобы ответы были верными. Выигрывает тот ученик, кто первым выполнит задание.

5х8+9х2=170

71-41:5= 6

65-27-12=50

64:7+1х9=72

6. Устный счёт «Из книги рекордов Гиннеса». Выразить в метрах:

а). Высота самого высокого смерча 1 км.528 м. Этот смерч был в Австралии.

б). Толщина самого толстого льда 4 км. 776м.

в). Вырази в минутах. Самая долгая радуга была видна в течение 3-х часов. Она наблюдалась в Англии.

г). Самый большой помидор выращен в Америке. Масса его была 3 кг.51г.

7. Учитель считает задания , дети записывают ответы в тетради.

а). Увеличьте 3120 на 8 сотен.

б). Первый множитель 42, второй – 20. Чему равно произведение?

в). Какое меньше 720 на 100?

г). Увеличьте 920 на 80.

д). Разность чисел 320 и 60.

е). Увеличьте 350 в 20 раз.

ё).  Из 86 тысячи вычти 4 единицы.

ж). Запишите наибольшее пятизначное число.

з). На сколько 267 больше 198?

В результате проверки на доске появляется запись:

3920	840	620	1000	260	7000	85996	99999	69
ж	с	с	у	а	д	а	й	р

Если вы расположите эти ответы в порядке возрастания, то расшифруете слово. Запишите его под ответами.

Какое это слово получилось?

Что это значит?

8. Игра “Иду в гости” Дети делятся на хозяев и гостей. Хозяева сидят за партами, у них конверты с карточками, на которых записаны примеры. Гости подходят к любому хозяину, тот даёт им карточки, Если гость правильно решил , то эту карточку он берёт себе и идёт к другому хозяину. У кого больше карточек, тот и выигрывает. Игра начинается и заканчивается сигналом.

Дополнительный материал на формирование вычислительных навыков.

Устный счет.

1. Какое животное может обходиться без пищи несколько дней.

11 жираф, 6 верблюд, 12 носорог 39 : 1 + 56 – 5 – 80 : 1 + 2 – 6 х 10 -14

2. Какое морское животное дышит воздухом. А детенышей вскармливает молоком:

58 дельфин, 86 акула, 51 кит 4 х 4 : 1 + 84 : 1 – 60 : 10 х 5 + 57 – 29

3. Какая рыба без чешуи?

3 сом, 67 щука, 84 окунь 100 : 1 – 96 : 2 х 9 х1 : 6 х 10 – 3 : 9.

4. Какой зверь самый чистоплотный?

12 еж, 4 заяц, 2 барсук 3х4 : 6 х 10 : 5 х 9 + 64 – 10 + 8 : 9.

5. Врачи утверждают, что если съесть 600 грамм этой свежей ягоды, то человек запасается витаминами на всю зиму. О какой лечебной ягоде идет речь?

65 черника 75 земляника, 95 клюква 24 + 41 : 10 + 7 : 2 х 1 + 13 : 2 + 65 х 1

6. Древесина какого дерева не гниет, а со временем становится тверже. Внутренние детали Московского Кремля сделаны из этого дерева и служат уже 500 лет.

57 кедр, 62 сосна, 74 лиственница 5 х 2 : 1 + 64 – 18 + 4 : 10 х 2 : 1 + 62

7. Этот русский ученый родился в Архангельской губернии, в рыбацкой семье, пешком отправился учиться в Москву. Стал поэтом, химиком. Фзиком. Астрономом. Кто он ?

45 Менделеев, 65 Ломоносов, 50 Попов 4 х 4: 2+ 12: 5 х 3+ 3 : 9 + 62

8. Кто из великих музыкантов в 28 лет начал глохнуть, в 48 лет окончательно потерял слух, но продолжал сочинять великую музыку до самой смерти.

60 Моцарт, 18 Чайковский, 57 Бетховен 3 х 3 : 1 – 1х 14 – 5: 2 + 81 : 10 : 3 + 54.

Задание. Запиши 4 шестизначных числа используя числа, 1, 03

Запиши 4 шестизначных числа, используя цифры 4, 2, 1

Составь из этих чисел различные суммы и найди их значение.

Составь из этих чисел различные разности и найди их значение.

Выполни записи в столбик и вставь цифры в «окошки», чтобы получились верные равенства:

3 86 + 2 7 = 2093

1 6 8 – 5 4 = 6669

308 24 – 3 521 = 7 3

А. 1. Вычислите значения выражений, соедините стрелкой выражение с

ответом:

63 + 6 99

54 + 20 28

36 + 40 74

23 + 5 69

92 +7 76

2. Разгадайте закономерность, по которой подобраны пары выражений.

Составьте по этому же правилу пары выражений с другими числами. Вычислите значение всех выражений:

15 + 2 62 + 4

51 + 20 26 + 40

3. Используя числа, составь верные равенства со знаком «+» и «–».

49, 5, 60, 83, 40, 89, 23, 34, 39.

Б. 1. Из чисел 3, 6, 4, 5, 8, 9, 2 выпишите четные числа; уменьшите их

на 5, результат увеличьте на 6; выпишите четные числа из полученных результатов.

2. Спишите числа 12; 2; 7; 6; 9; 3; 5; 4; 8; 1, подчеркните те числа, сумма которых равна 13; числа, сумма которых равна 8, зачеркните.

3. Выберите из чисел те, которые меньше 10, но больше 6; увеличьте каждое на 5, а результат уменьшите на 6; запишите ответы 2; 9;7; 5; 10; 8.

В. 1. Вместо точек вставьте пропущенные цифры в данные числа так,

чтобы каждое следующее число:

- уменьшалось на 2 единицы: .. 9, 6.., 6.., 6..

- увеличивалось на 2 десятка: ..3, ..3, ..3, ..3.

2. Запишите выражения в два столбика: в первый – сумма, во второй –

разность. Найдите их значения. Сравните приемы вычислений.

27 + 2 59 - 4

27 + 20 39 - 10

27 - 20 27 - 2

59 +4 59 - 40

59 + 40

3. Запишите выражения в два столбика так, чтобы в каждом столбике

были выражения, похожие по способу нахождения их значений. Найдите

значения выражений.

57 + 2 46 - 30

58 + 20 41 + 7

19 - 5 36 +20

72 - 40 94 - 50

Г. 1. Найдите значения выражений, записывая подробно объяснения:

67 + 3 = (60 + 7) + 3 = 60 + 10 = 53 + 7 = (50 +...) +...

42 + 8 = (.. +..) +..

31 + 9 =

2. Выберите из предложенных чисел такие пары, сумма которых будет

равна 70. Запишите эти суммы: 54, 6, 64, 62, 8, 9, 7, 63, 51, 61, 3, 67, 73.

3. Решите удобным способом:

(38 + 8) + 2

(7 + 20) + 3

(2 + 40) + 8

(70 + 1) + 9

Какой вычислительный прием изучался в процессе выполнения каждой тройки заданий?

Задание 4. Составьте аналогичные задания для изучения вычислительных приемов вида 30 - 6; 42 - 5. Запишите их в ту же таблицу.

Тема 4. Использование приемов умственных действий при формировании умений и навыков устных вычислений.

Задание 1. Какие приемы умственных действий используются при выполнении упражнений?

а) Пользуясь записанным выражением 34 + 26, отметь верные высказывания:

«Число 34 увеличили на 26 и получили 70».

«Число 60 меньше, чем число 26 на 34».

«Число 34 меньше, чем число 60 на 26».

«Сумма чисел 34 и 26 равна 60».

б) На какие две группы можно разбить выражения:

24 + 3, 78 + 6, 24 + 7, 62 + 9, 84 + 8, 84 + 5, 62 + 6, 78 + 1?

в) Найди значения выражений. Догадайся, какая пара «лишняя»:

43 + 9 64 + 8 35 + 4 46 - 7

43 - 9 64 - 8 35 - 4 46 + 7 ?

г) Чем похожи выражения в каждом столбике? Объясни, как ты будешь вычислять значение разности.

69 - 6 83 - 30 26 - 2 96 - 60

38 - 3 54 - 40 57 - 5 42 - 20

д) Чему равна первая сумма чисел? Как найти значения двух других

выражений, не складывая записанные числа?

21 + 30 + 11 + 12

22 + 31 + 12 +13

23 + 32 + 13 +14

е) Чем похожи записи? Какой вывод можно сделать?

13 - 8 = 13 - (3 + 5) = (13 - 3) - 5 = 10 - 5 = 5

17 - 9 = 17 - (7 + 2) = (17 - 7) - 2 = 10 - 2 = 8

11 - 4 = 11 - (1 + 3) = (11 - 1) - 3 = 10 - 3 = 7

ж) Разгадай правило, по которому составлены выражения в каждом столбике. Найди значение второго выражения, используя значение первого

выражения.

78 + 2 + 4 37 + 3 + 5 49 + 1 + 6 58 + 2 +7

78 + 6 37 + 8 49 + 7 58 + 9.

з) Догадайся, как можно найти значения выражений:

8+1=9 2+3=5 4+2=6

80 + 10 = [ ] 20 + 30 = [ ] 40 + 20 = [ ]

Для раскрытия переместительного свойства сложения использовалась игра «Было – стало».

Дидактическая цель. Ознакомление с переместительным свойством сложения.

Содержание игры. Учитель закрепляет на магнитной доске рисунок елочки. На ее ветках он «развешивает» слева 13 игрушек, а справа – 22.

С помощью раздаточного материала дети украшают так же свои елочки на партах. По рисункам составляется и записывается на доске пример на сложение:13+22.

После того как он будет решен, учитель просит детей закрыть глаза и переставляет рисунки игрушек. Открыв глаза, дети замечают, что изменилось, и тоже меняют местами свои рисунки. По новой иллюстрации составляется еще один пример на сложение: 12+23. Решив его, первоклассники получают тот же ответ:. Несколько раз поменяв местами различное число игрушек на левых и правых ветках ели и составив3-4 пары примеров на сложение, можно подвести учащихся к выводу: от перестановки слагаемых сумма не изменяется.

Чтобы дети научились применять прием перестановки слагаемых в тех случаях, когда это облегчает вычисления, использовалась игра «Капитаны»

«Капитаны»

Дидактическая цель. Закрепление знания прибавления и вычитания 25, 26, 27, 28, и 29.

Содержание игры. На магнитной доске учитель размещает рисунки пароходов и записывает под каждым пример вида: +5, +6, +7,

+8, +9. Справа от рисунков он закрепляет ряд карточек с цифрами 1, 2, 3, 4, 5, 6, 7, 8, 9 ,10 и пишет над ними: « Пристани».

До начала игры детям рассказывается: « Многое должен знать капитан, чтобы идти намеченным курсом. Представьте себе, что на море шторм, пароход качает из стороны в сторону. Любая ошибка в расчетах может потопить его, погибнут люди».

Учитель вызывает 3-4 учеников (капитанов) к доске и объясняет: «Курс каждого корабля зашифрован примером, а его пристань обозначена номером. Каждый «капитан» должен определить «курс движения» (решить пример под выбранным им рисунком), а потом причалить свой корабль к нужной «пристани», где находится его номер (ответ примера). Кто раньше всех встанет на свое место у пристани, то и будет лучшим капитаном».

Игра «Самый быстрый почтальон»

Дидактическая цель. Закрепление случаев прибавления и вычитания в пределах 100.

Средства обучения. Листки бумаги и разрезные цифры.

Содержание игры. Учитель раздает пяти ученикам по одинаковому числу карточек (писем), на обратной стороне которых записаны выражения на сложение и вычитание. Дети, сидящие за партами, изображают дома с номерами. Они держат в руке разрезные цифры, обозначающие числа от 0 до 100. Самые быстрые почтальоны должны быстро определить на конверте номер дома, записанного выражением (найти значение выражения), и разнести письма в соответствующие дома (отдать детям, у которых карточки с цифрами, обозначающими значения выражений, записанных на конвертах). Кто быстро и правильно разнесет письма по назначению, тот – самый быстрый почтальон. Полученные решения проверяют все ученики.

На этапе закрепления можно провести дидактическая игру, которая требует знания компонентов сложения, переместительного свойства сложения, состава чисел и взаимосвязи сложения и вычитания.

«Математическая эстафета»

Дидактическая цель. Формирование умения преобразовывать одни выражения в другие, логически связанные с ними.

Содержание игры. Класс разбивается по рядам на 3 команды. Для каждой команды учитель пишет выражения:

16+12 15+14 17+13

К доске выходят по одному ученику одновременно от каждой команды. Их задача состоит в том, чтобы правильно и быстро найти значение выражения, составить другое выражение с этими числами и передать эстафету своему участнику. Учащиеся по командам составляют цепочку взаимосвязанных выражений вида:

16+12=28 15+14=29 17+13=30

12+16=28 14+15=19 13+17=30

18-12=6 19-14=5 20-7=13

18-16=2 19-5=14 20-3=17

Игра продолжается до тех пор, пока ученики каждой команды не составят все выражения с этими числами. Побеждает та команда, которая раньше других составит правильно цепочку взаимосвязанных выражений.

Таким образом, при формировании вычислительных навыков нужно опираться на теоретические основы вычислительных приемов: определение арифметических действий, свойство и следствия, вытекающие из них, которые рассмотрены в теоретической части нашей работы.

3.3 Анализ опытно-экспериментальной работы

Цель контрольного эксперимента – установить эффективность проделанной работы .

С этой целью мы провели в экспериментальном классе самостоятельную работу по теме «Сложение и вычитание многозначных чисел».

1 вариант

1. Запиши число 575116 в виде суммы разрядных слагаемых.

2. Продолжи ряды чисел:

12496, 12497, 12498….

810004, 810003, 810002…

3. Сравни числа 12224…33241

27954…20975

472870 …472807

558540…35540

4. Найди значение выражения:

53655 + 71568 =

328783 + 246565 =

35306 – 23687 =

926206 – 795378 =

П вариант .

1. Запиши число 694382 в виде суммы разрядных слагаемых.

Продолжи ряды числе:

21697, 21698, 21699…

640003, 640002, 640001…

Сравни числа: 84474…39364

74235… 70532

248208…248280

272696…53037

4. Найди значение выражения

24798 + 63066

426646 + 324857

67964 – 54694

956420 – 687693

По результатам самостоятельной работы были получены следующие оценки:

На 5 написали – 5 человек

На 4 написали 7 человека

На 3 написали 3 человек

Таким образом, уровень сформированности вычислительных навыков можно представить в следующей таблице:

Табл . 2

Уровни сформированности вычислительных навыков младших школьников

КЛАСС	Уровни сформированности математических знаний младших школьников, %
	Оптимальный	Допустимый	Недопустимый
3 кл. 15 чел.	33, 3	66, 7%	0

Представим результаты для большей наглядности в следующем графике:

Рис. 2 Уровень сформированности вычислительный навыков у учащихся 3 класса на этапе контрольного эксперимента

Оптимальный уровень

Допустимый уровень

У всех учащихся третьего класса сформированы вычислительные навыки на оптимальном и достаточном уровне. Для сравнения результатов констатирующего и контрольного экспериментов можно отразить в таблице

Табл. 3

	Оптимальный	Допустимый	Недопустимый
Констатирующий Контрольный	20% 33, 3%	73, 3 66, 7	6, 7

Таким образом, достаточное число разнообразных упражнений на применение вычислительных приемов в формирующем эксперименте позволило получить следующие результаты: оптимальный и допустимый уровень сформированности вычислительных навыков составляет 100% Это свидетельствует о том, что правильное выделение стадий формирования вычислительных навыков позволило учителю управлять процессом усвоения учащимися вычислительных приемов, то есть формирование вычислительных навыков.

Заключение

Задача формирования вычислительных навыков является центральной в курсе математики начальных классов. Но было бы ошибкой решать эту задачу только путем зазубривания таблиц сложения и умножения и использования их при выполнении однообразных тренировочных упражнений.

В процессе работы на формирование вычислительных навыков подбор разнообразных упражнении и дидактических игр как по форме, так и по числовым данным развивает у учащихся познавательный интерес, творческую активность, потребность в знаниях. Но, безусловно, качество формирования вычислительных навыков зависит и от количества выполняемых тренировочных упражнений.

Целью нашей работы было изучение использования дидактической игры для формирования вычислительных навыков на уроках математики в начальной школе. Для этого мы изучили педагогическую и методическую литературу по теме исследования; виды дидактических игр; рассмотрели проблему формирования вычислительных навыков младших школьников в современных условиях; изучили систему формирования вычислительных навыков младших школьников и методику их формирования. В опытно-экспериментальной работе мы проверили правильность выводов, сделанных в теоретической части нашей работы. Таким образом, применение дидактической игры на уроках математики позволило учителю управлять процессом усвоения учащимися вычислительного приема, постепенного свертывания выполнения операций, образования вычислительных навыков. Список литературы

1. Антонович, Н. X. Математические игры для учащихся третьих классов / Н. Х Антонович // Математика в школе. — 1965.— № 5.— 245 с;
2. Бантова, М. А. Система формирования вычислительных навыков / М. А. Бантова // Начальная школа . – 1993. – № 11. – С. 38-45.
3. Жикалкина, Т. К. Игровые и занимательные задания по математике для 2 класса 4-ех летней начальной школы : пособ. для учит. – М. : Просвещение, 1987. – 63 с.
4. Захарова, С. И. Математику учим в игре / С. И. Захарова // Начальная школа. – 1999. – № 8. – С. 40-42.
5. 3имний, А. И. Элементы игры на уроках математики / А. И. Зимний // Математика в школе.– 1977. – № 6. – С. 33-35.
6. Истомина Н.Б., Клецкина А.А.
   Тетрадь №1 по математике для 3-го класса четырехлетней начальной школы. Ч. 1.- Смоленск: Ассоциация ХХI век, 2001 (Смоленск: Смоленский полиграфический комбинат Министерства РФ по делам печати, ГУП).- 64 с. : ил.;- ISBN 5-89308-050-5
7. Истомина Н.Б., Клецкина А.А.Тетрадь №2 по математике для 3-го класса четырехлетней начальной школы. Ч. 2.- Смоленск: Ассоциация ХХI век, 2001 (Смоленск: Смоленский полиграфический комбинат Министерства РФ по делам печати, ГУП).- 48 с. : ил.; - ISBN 5-89308-049-1 (В обл.)
8. Истомина, Н. Б. Математика 3 класс. : учеб. для четырехлетней начальной школы / Н. Б. Истомина – М. : Смоленск, : Московские учебник, 2000. –178 с.
9. Истомина, Н. Б. Методика обучения математике в начальных классах / Н. Б.Истомина – М. : Просвещение, 2001 – 356 с.
10. Истомина, Н. Б. Методические рекомендации к учебнику « Математика. 3 класс» для четырехлетней школы – Смоленск, 2001.

11. Карпова, Е. В. Дидактические игры в начальный период обучения / Е. В. Карпова.- Ярославль, 1997.- 240 с.

12. Кордемский, Б. А. Увлечь школьников математикой Б. А. Кордемский – М.: Просвещение, 1981. – 156 с.
13. Кроль, В. М. Психология и педагогика : учеб. пособ. для вузов / В. М. Кроль – М. : Высш. шк.– 2003. – 325 с.
14. Кукушкин, В. С. Современные педагогические технологии : нач. школа : пособ. для учит. / В. С. Кукушкин – Ростов – н / Дону – Феникс, 2004. – 384 с.
15. Кураченко, З. В. Личностно-ориентированный подход в системе обучения математике / З. В. Кураченко // Начальная школа. – 2004. – № 4. – С. 60-65.
16. Лавриненко, Т.А. Задания развивающего характера по математике. Саратов, 2002. – 204 с.
17. Левитас Г.Г. Нестандартные задачи по математике / Г. Г. Левитас – М. : Педагогика, 2002. – 301 с.
18. Матасова, Н. В. Математика : 3 класс : Ч 1-2. : поурочные планы по учебнику Н. Б. Истоминой – Волгоград : Учитель- АСТ, – 2004.
19. Математика : учеб. для 3 класса начальной школы. В 2-х частях. / М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. – 4-е изд. – М. : Просвещение, 2003.
20. Минкин, Е. М. От игры к знаниям / Е. М. Минкин : Просвещение, 1982. – 78 с;
21. Редакова, Е. М. Создание игровых компонентов и их применение в обучении младших школьников / Е. М. Редакова, Л. М. Новокшонова // Начальная школа. - 2000. – № 11. – С. 77-83.
22. Русанов В.Н. Математические олимпиады младших школьников. М. : Просвещение, 1990 – 287 с.
23. Селеванов, В. С. Основы общей педагогики : теория и методика воспитания : учеб. пособ. для студ. пед. вузов / В. С. Селиванов – 2-е изд. , испр. – М. : Академия, 2002.
24. Ситаров, В. А. Педагогика / В. А. Ситаров, ; под ред. В. А. Сластенина – М. : Академия, 2004. – 368 с.
25. Спиваковская, А. С. Игра - это серьезно / А. С. Спиваковская М.:Педагогика,1981. – 96 с;
26. Тихомирова, Л. Ф. Математика в начальных классах : развивающие игры, задания, упражнения : пособ. для учителей нач. кл., воспита. дет. садов / Л. Ф. Тихомирова М. : Сфера, 2003. – 96 с. ISBN 5-89-144-175-6.
27. Чилингорова, Л. А. Играя, учимся математике / Л. А. Чилингорова – М. : Просвещение, 1993. – 145 с;
28. Чутчева, Е.Б. Занимательные задачи по математике. М. : Педагогика, 1996 – 215 с.