Задачи на среднее, медиану и т.д.

1.  В течение четверти оценки Вовы распределились следующим образом: двоек  — 4, троек  — 6, четвёрок  — 7 и пятёрок  — 5. Учитель предложил на выбор три способа выведения четвертной оценки.

Первый способ: оценка равна среднему арифметическому полученных оценок с последующим округлением до целого числа при необходимости. Второй: оценка равна моде всего ряда оценок. Третий способ: оценка равна медиане всего ряда полученных оценок с округлением до целого при необходимости. Какой способ является наиболее выгодным и какой  — наименее выгодным для Вовы?

Решение. Среднее арифметическое Вовиных оценок равно их сумме, делённой на количество, то есть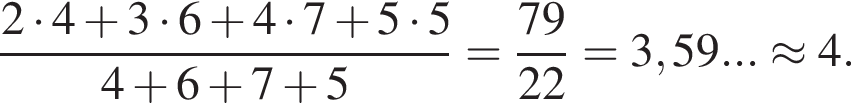

В первом случае с учётом округления Вова получит оценку 4.

Мода ряда оценок равна 4, так как именно эта оценка встречается чаще всего. Итак, во втором случае Вова также получит четвёрку.

Для определения медианы запишем выборку в виде вариационного ряда: 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5. Количество элементов чётно, поэтому медиана равна полусумме 11 и 12 вариант, то есть 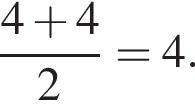 Ответ: Все 3 способа одинаково выгодны.

2.  В течение полугодия оценки Саши распределились следующим образом: двоек  — 1, троек  — 5, четвёрок  — 2 и пятёрок  — 3. Учитель предложил на выбор три способа выведения четвертной оценки.

Первый способ: оценка равна среднему арифметическому полученных оценок с последующим округлением до целого числа при необходимости. Второй: оценка равна моде всего ряда оценок. Третий способ: оценка равна медиане всего ряда полученных оценок с округлением до целого при необходимости. Какой способ является наиболее выгодным и какой  — наименее выгодным для Саши?

Решение. Среднее арифметическое Сашиных оценок равно их сумме, делённой на количество, то есть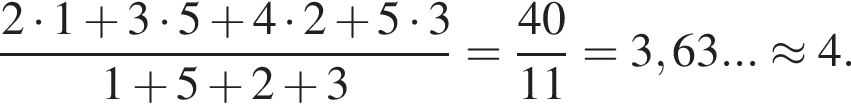

В первом случае с учётом округления Саша получит оценку 4.

Мода ряда равна 3, так как именно эта оценка встречается чаще всего. Итак, во втором случае Саша получит тройку.

Для определения медианы запишем выборку в виде вариационного ряда: 2, 3, 3, 3, 3, 3, 4, 4, 5, 5, 5. Количество элементов нечётно, поэтому медиана равна шестой варианте, то есть тройке.

 Ответ: Наиболее выгоден первый способ, наименее  — второй и третий.

3.  Мальчик записал в блокноте некоторую выборку из 6 чисел, но неаккуратно вырвал листок, и в результате последнее число оказалось утрачено. Сохранились первые числа: −3; 1; 4; −2; 3. Восстановите утраченное число, если известно, что медиана выборки равна 2.

Решение. Пусть неизвестное число равно x. Запишем выборку без x в виде вариационного ряда: −3; −2; 1; 3; 4. Рассмотрим 3 возможных случая расположения неизвестного числа в выборке.

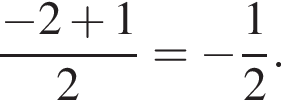Если то медиана будет равна Случай не подходит.

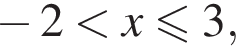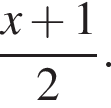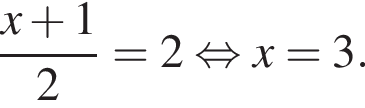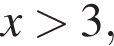Если то медиана будет равна Тогда Если то медиана будет равна Тогда

Объединяя полученные решения, получаем, что медиана выборке равна 2 при  

Ответ: [3;  +∞).

4.  Мальчик записал в блокноте некоторую выборку из 6 чисел, но неаккуратно вырвал листок, и в результате последнее число оказалось утрачено. Сохранились первые числа: 0; −2; −5; 3; −1. Восстановите утраченное число, если известно, что медиана выборки равна −1.

Решение. Пусть неизвестное число равно x. Запишем выборку без x в виде вариационного ряда: −5; −2; −1; 0; 3. Рассмотрим 3 возможных случая расположения неизвестного числа в выборке.

Если то медиана будет равна Случай не подходит.

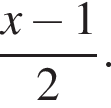Если то медиана будет равна Тогда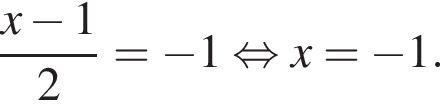

Если 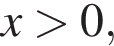то медиана будет равна 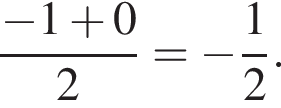Случай не подходит.

Ответ: −1.

5.  Студент обнаружил, что за семестр он получил 18 оценок по математическому анализу. У него записаны следующие оценки:

пятёрок  — 8, двоек, троек и четвёрок по 3. Одна оценка не записана. Когда студент спросил об этой оценке преподавателя, тот сказал, что среднее арифметическое всех оценок  — целое число. Какая оценка не записана?

Решение. Пусть неизвестная оценка равна x. Тогда необходимо, чтобы дробь

была целым числом. Наименьшее число, большее 67 и кратное 18, равно 72. В таком случае неизвестная оценка равна 72 − 67  =  5.

 Ответ: 5.

6.  Школьник обнаружил, что за год он получил 28 оценок по математике. У него записаны следующие оценки: пятёрок  — 17, одна четвёрка, 3 тройки и 6 двоек. Одна оценка не записана. Когда школьник спросил об этой оценке у учителя, он ответил, что среднее арифметическое всех оценок  — целое число. Какая оценка не записана дневнике?

Решение. Пусть неизвестная оценка равна x. Тогда необходимо, чтобы дробь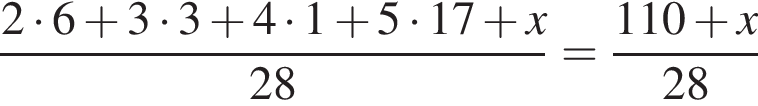

была целым числом. Наименьшее число, большее 110 и кратное 28, равно 112. В таком случае неизвестная оценка равна 112 − 110  =  2.

 Ответ: 2.

1.  В течение четверти оценки Вовы распределились следующим образом: двоек  — 4, троек  — 6, четвёрок  — 7 и пятёрок  — 5. Учитель предложил на выбор три способа выведения четвертной оценки.

Первый способ: оценка равна среднему арифметическому полученных оценок с последующим округлением до целого числа при необходимости. Второй: оценка равна моде всего ряда оценок. Третий способ: оценка равна медиане всего ряда полученных оценок с округлением до целого при необходимости. Какой способ является наиболее выгодным и какой  — наименее выгодным для Вовы?

2.  В течение полугодия оценки Саши распределились следующим образом: двоек  — 1, троек  — 5, четвёрок  — 2 и пятёрок  — 3. Учитель предложил на выбор три способа выведения четвертной оценки.

Первый способ: оценка равна среднему арифметическому полученных оценок с последующим округлением до целого числа при необходимости. Второй: оценка равна моде всего ряда оценок. Третий способ: оценка равна медиане всего ряда полученных оценок с округлением до целого при необходимости. Какой способ является наиболее выгодным и какой  — наименее выгодным для Саши?

3.  Мальчик записал в блокноте некоторую выборку из 6 чисел, но неаккуратно вырвал листок, и в результате последнее число оказалось утрачено. Сохранились первые числа: −3; 1; 4; −2; 3. Восстановите утраченное число, если известно, что медиана выборки равна 2.

4.  Мальчик записал в блокноте некоторую выборку из 6 чисел, но неаккуратно вырвал листок, и в результате последнее число оказалось утрачено. Сохранились первые числа: 0; −2; −5; 3; −1. Восстановите утраченное число, если известно, что медиана выборки равна −1.

5.  Студент обнаружил, что за семестр он получил 18 оценок по математическому анализу. У него записаны следующие оценки: пятёрок  — 8, двоек, троек и четвёрок по 3. Одна оценка не записана. Когда студент спросил об этой оценке преподавателя, тот сказал, что среднее арифметическое всех оценок  — целое число. Какая оценка не записана?

6.  Школьник обнаружил, что за год он получил 28 оценок по математике. У него записаны следующие оценки: пятёрок  — 17, одна четвёрка, 3 тройки и 6 двоек. Одна оценка не записана. Когда школьник спросил об этой оценке у учителя, он ответил, что среднее арифметическое всех оценок  — целое число. Какая оценка не записана дневнике?