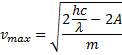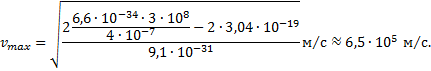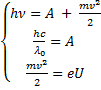Молекулярная физика
ЗАДАЧА 1.
При температуре 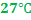 и давлении
и давлении 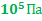 объем воздушного шара, заполненного гелием, равен
объем воздушного шара, заполненного гелием, равен 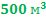 . Каким будет объем этого шара, если при подъёме в верхние слои атмосферы температура понизится до
. Каким будет объем этого шара, если при подъёме в верхние слои атмосферы температура понизится до 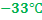 , а давление станет равным
, а давление станет равным 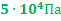 ? Массу гелия считать постоянной.
? Массу гелия считать постоянной.
Дано:
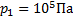
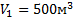
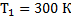

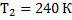
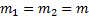
______________
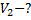
Решение:
Из уравнения состояния идеального газа
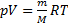 следует, что при условии
следует, что при условии 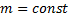
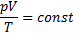
Поэтому выполняется равенство
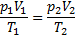
Из него получаем:
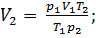
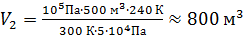 Ответ:
Ответ: 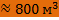
ЗАДАЧА 2.
Вычислите кинетическую энергию теплового движения всех молекул воздуха в физическом кабинете. Объем кабинета – 140 м3, давление воздуха – 105 Па. Сколько воды можно было бы нагреть от 0 до 100 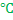 при полном использовании этой энергии?
при полном использовании этой энергии?
Дано:
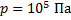
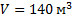
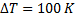

_______________________
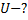
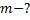
Решение:
Считая, что свойства воздуха близки к свойствам идеального газа, применим для вычисления кинетической энергии хаотического теплового движения всех его молекул формулу:

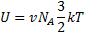
Используя равенство 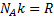 , получим:
, получим:
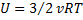
Так как из уравнения состояния идеального газа следует, что
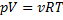 , то
, то
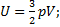
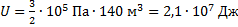
Для вычисления массы нагреваемой воды запишем уравнение теплового баланса
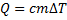
и выразим из него массу m:
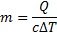
По условию задачи 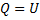 , поэтому масса нагреваемой воды равна
, поэтому масса нагреваемой воды равна
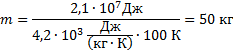 Ответ:
Ответ: 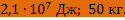
ЗАДАЧА 3.
Как изменится объем пузырька воздуха при всплывании его со дна озера глубиной 20 м к поверхности воды? Температура воды у дна озера и у поверхности одинакова. Атмосферное давление принять равным 105 Па.
Дано:
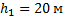
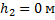
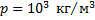
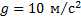
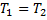
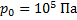
_____________
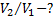
Решение:
Объем пузырька воздуха при всплывании будет изменяться из-за уменьшения давления. Так как температура воды одинакова у дна озера и у поверхности воды, изменение объема воздуха будет происходить в результате его изотермического расширения.
При изотермическом процессе давление и объем газа связаны соотношением:
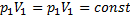
 Отсюда
Отсюда
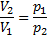
Давление 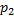 у поверхности воды равно внешнему атмосферному давлению. Давление
у поверхности воды равно внешнему атмосферному давлению. Давление  на глубине h складывается из внешнего атмосферного давления и давления водяного столба:
на глубине h складывается из внешнего атмосферного давления и давления водяного столба:
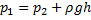
Подставляя численные значения величин, получаем:
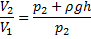
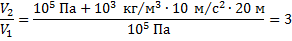
Ответ: объем пузырька увеличится в 3 раза.
ЗАДАЧА 4.
Постройте график изотермического процесса идеального газа при температуре 300 К. Начальное давление и объем соответственно равны 9 Па и 2 м3, конечное давление равно 2 Па.
Решение:
Для построения графика изотермического процесса в координатных осях p, V будем отсчитывать по оси абсцисс значения объема газа, по оси ординат – значения давления. Масштаб выберем таким, чтобы начальные и конечные значения давления и объема укладывались на графике. Точку графика, соответствующего начальному состоянию газа, найдем на пересечении двух прямых: параллельной оси ординат, - она пересекает ось абсцисс в точке 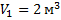 , и параллельной оси абсцисс, - пересекает ось ординат в точке
, и параллельной оси абсцисс, - пересекает ось ординат в точке 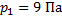 .
.
Для нахождения остальных точек графика необходимо воспользоваться уравнением изотермического процесса:
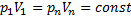
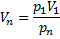 и найти значения объема
и найти значения объема 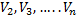 , соответствующие выбранным значениям давления
, соответствующие выбранным значениям давления 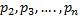 до конечного значения. Выберем следующий ряд значений давления:
до конечного значения. Выберем следующий ряд значений давления:
| p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 |
| 9 Па | 8 Па | 7 Па | 6 Па | 5 Па | 4 Па | 3 Па | 2 Па |
Для каждого выбранного значения 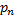 вычислим соответствующее ему значение объема
вычислим соответствующее ему значение объема 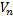 . Результаты вычислений представлены таблице.
. Результаты вычислений представлены таблице.
По найденным значениям объема газа при выбранных значениях давления нанесем точки, через точки проведем линию. Она и будет графиком изотермического процесса в координатных осях p, V (см. рисунок 1).
Построение графиков изотермического процесса в координатных осях p,T и V,T является более простой задачей.
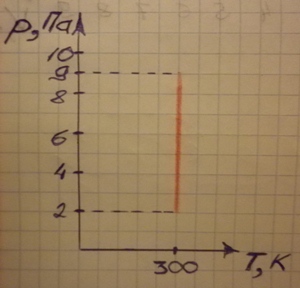 При выборе оси абсцисс для отсчета значений температуры газа графики изотермических процессов представляют собой прямые, параллельные оси ординат (см. рисунок 2 и рисунок 3). Продолжение этих прямых до оси абсцисс пересекает ее в точках, соответствующих значениям температуры изотермического процесса. Ординаты верхней и нижней точек этих графиков определяются начальными и конечными значениями объема газа (рис. 2) и его давления (рис. 3).
При выборе оси абсцисс для отсчета значений температуры газа графики изотермических процессов представляют собой прямые, параллельные оси ординат (см. рисунок 2 и рисунок 3). Продолжение этих прямых до оси абсцисс пересекает ее в точках, соответствующих значениям температуры изотермического процесса. Ординаты верхней и нижней точек этих графиков определяются начальными и конечными значениями объема газа (рис. 2) и его давления (рис. 3).
ЗАДАЧА 5.
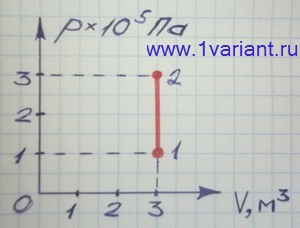
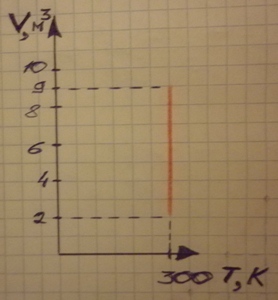
По графику процесса, осуществленного с идеальным газом (рисунок 1), постройте графики этого процесса в координатных осях p,T и V,T. Температура газа в начальном состоянии 1 была равна 250 К.
Решение:
График на рисунке 1 показывает, что давление газа при переходе из состояния 1 в состояние 2 увеличилось в 3 раза, а объем в течение всего процесса оставался неизменным. Следовательно, процесс изменения состояния газа был изохорным. При изохорном процессе связь между давлением газа p и абсолютной температурой T выражается уравнением:
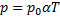
Из этого уравнения следует, что отношение давления газа p к абсолютной температуре Т при изохорном процессе является постоянной величиной:
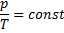
или
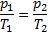
Отсюда
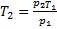
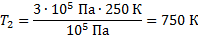
 По известным начальным и конечным значениям давления и температуры построим в системе координат с осями p,T точки 1 и 2, соответствующие начальному и конечному состояниям газа. Зависимость давления p от температуры Т линейная, - следовательно, график изохорного процесса в координатных осях p,T является прямой, проходящей через точки 1 и 2 (рисунок 2).
По известным начальным и конечным значениям давления и температуры построим в системе координат с осями p,T точки 1 и 2, соответствующие начальному и конечному состояниям газа. Зависимость давления p от температуры Т линейная, - следовательно, график изохорного процесса в координатных осях p,T является прямой, проходящей через точки 1 и 2 (рисунок 2).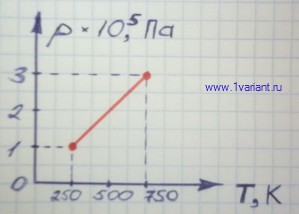
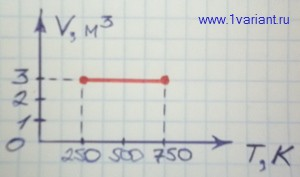
В координатных осях V,T график изохорного процесса – это отрезок прямой, параллельной оси абсцисс, с ординатой, равной объему газа. Концы отрезка определяются прямыми, параллельными оси ординат и проходящими через точки на оси абсцисс, соответствующие значениям начальной и конечной температуры (рисунок 3).
ЗАДАЧА 6.
Каким должен быть радиус капиллярной трубки для того, чтобы при полном смачивании вода в капилляре поднялась на 10 см? Коэффициент поверхностного натяжения воды равен 
Дано:
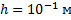
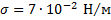
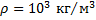
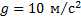
______________
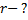
Решение:
При полном смачивании модуль силы поверхностного натяжения, действующей по линии соприкосновения жидкости со стенкой капилляра, равен модулю силы тяжести поднявшегося столба жидкости:
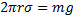
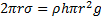
Из этого равенства следует:
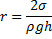

Ответ: 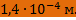
ЗАДАЧА 7.
Какой диаметр должен иметь стальной трос подъемного крана, если максимальная масса поднимаемого груза равна 10 тонн? Предел прочности стальной проволоки 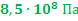 . Запас прочности должен быть равен 6.
. Запас прочности должен быть равен 6.
Дано:
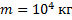
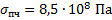
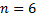 _______________
_______________
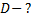
Решение:
Предел прочности определяется отношением модуля максимальной силы упругости к площади поперечного сечения:
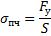
Так как запас прочности равен 6, трос должен выдерживать нагрузку, в 6 раз превышающую ту, которая возникает при подъеме груза массой 10 т. Следовательно,
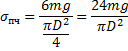
Отсюда диаметр троса равен:
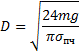
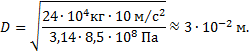
Ответ: 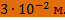
ЗАДАЧА 7.
Какой диаметр должен иметь стальной трос подъемного крана, если максимальная масса поднимаемого груза равна 10 тонн? Предел прочности стальной проволоки 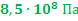 . Запас прочности должен быть равен 6.
. Запас прочности должен быть равен 6.
Дано:
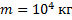
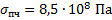
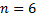
________________
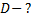
Решение:
Предел прочности определяется отношением модуля максимальной силы упругости к площади поперечного сечения:
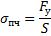
Так как запас прочности равен 6, трос должен выдерживать нагрузку, в 6 раз превышающую ту, которая возникает при подъеме груза массой 10 т. Следовательно,
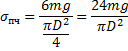
Отсюда диаметр троса равен:
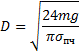
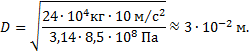
Ответ: 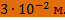
ЗАДАЧА 9.
Определите максимальный КПД тепловой машины, если температура нагревателя равна 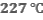 , а температура холодильника
, а температура холодильника 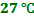 .
.
Дано:
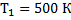
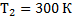
_________
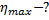
Решение:
Максимальный КПД тепловой машины определяется выражением:
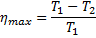

Ответ: 0,4.
ЗАДАЧА 10.
В теплоизолированном сосуде находятся вода и лед при температуре  . Массы воды и льда соответственно равны 0,5 кг и 60 г. В воду впускается водяной пар массой 10 г при температуре
. Массы воды и льда соответственно равны 0,5 кг и 60 г. В воду впускается водяной пар массой 10 г при температуре 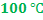 . Какой станет температура воды в сосуде после установления теплового равновесия? Теплоемкость сосуда в расчетах не учитывать.
. Какой станет температура воды в сосуде после установления теплового равновесия? Теплоемкость сосуда в расчетах не учитывать.
Дано:
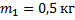
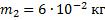
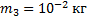
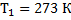
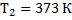
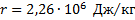
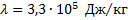

_______________________
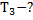
Решение:
Проверим сначала, достаточно ли выделяющегося при конденсации пара количества теплоты Q3 для плавления льда. При конденсации пара выделяется количество теплоты Q3:
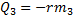
Для плавления льда требуется количество теплоты Q2:
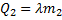
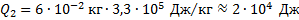
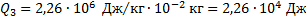
Сравнение количеств теплоты Q3 и Q2 показывает, что 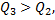 поэтому уравнение теплового баланса имеет вид:
поэтому уравнение теплового баланса имеет вид:
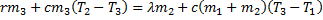
Теплота выделяется при конденсации пара массой 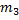 и остывании сконденсировавшейся воды от температуры
и остывании сконденсировавшейся воды от температуры 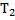 до некоторого значения
до некоторого значения 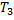 , а поглощается при плавлении льда массой
, а поглощается при плавлении льда массой 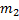 и нагревании воды массой
и нагревании воды массой 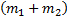 от температуры
от температуры 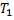 до равновесного значения
до равновесного значения 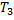 .
.
Обозначив 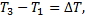 для разности
для разности 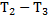 получим:
получим:
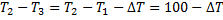
Уравнение теплового баланса приобретает вид:
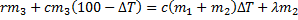
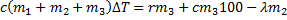
Откуда
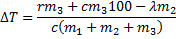
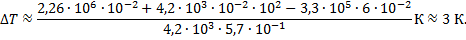
Тогда 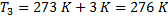 .
.
Ответ: 276 К.
МЕХАНИКА. РЕШЕНИЕ ЗАДАЧ.
ЗАДАЧА 1.
После удара о поверхность Земли мяч движется вертикально вверх со скоростью 15 м/с. Найдите координату мяча над поверхностью Земли через 1 с и через 2 с после начала движения. Дайте объяснение полученному результату.
Дано:
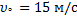
g = 10 м/с2
h○ = 0 м
t1 = 1 c
t2 = 2 c
__________
y1 = ? y2 = ?
Решение:
Координата тела при равноускоренном прямолинейном движении определяется по формуле:
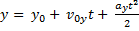
Координатную ось ОY направим по вертикали вверх, начало отсчета находится на поверхности Земли. Тогда
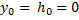
Так как направление вектора начальной скорости 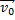 совпадает с направлением оси OY, а направление вектора
совпадает с направлением оси OY, а направление вектора  противоположно направлению оси OY, то проекция начальной скорости
противоположно направлению оси OY, то проекция начальной скорости 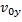 положительна, а ускорения
положительна, а ускорения 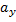 отрицательна:
отрицательна:
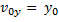 ,
, 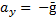
Тогда
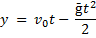
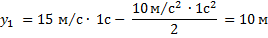
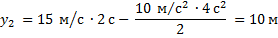
Через 1 с и через 2 с после начала движения мяч находится в одной и той же точке пространства. В момент времени 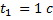 он проходит через эту точку во время движения вверх, в момент времени
он проходит через эту точку во время движения вверх, в момент времени 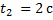 - во время движения вниз.
- во время движения вниз.
ЗАДАЧА 2.
Лодка движется перпендикулярно берегу реки. Её скорость относительно воды равна 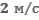 . Определите время движения лодки к другому берегу, если ширина реки 80м, а скорость течения
. Определите время движения лодки к другому берегу, если ширина реки 80м, а скорость течения 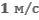 .
.
Дано:
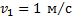
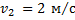

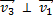
____________
t - ?
Решение:
Для нахождения времени движения лодки через реку необходимо найти скорость лодки относительно берега. Скорость 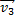 лодки относительно берега равна сумме векторов
лодки относительно берега равна сумме векторов 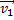 (скорости течения воды) и
(скорости течения воды) и 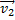 (скорости лодки относительно воды):
(скорости лодки относительно воды):
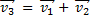
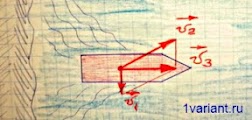
Вектор 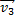 скорости лодки относительно берега перпендикулярен вектору
скорости лодки относительно берега перпендикулярен вектору 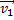 скорости течения реки. В векторном треугольнике они являются катетами, а вектор
скорости течения реки. В векторном треугольнике они являются катетами, а вектор 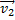 – гипотенузой. Модуль вектора
– гипотенузой. Модуль вектора 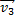 изэтого треугольника равен:
изэтого треугольника равен:
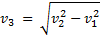
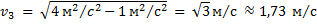
Время t движения лодки от одного берега к другому равно
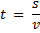
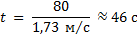 Ответ: 46 секунд.
Ответ: 46 секунд.
ЗАДАЧА 3.
Человек массой 60 кг катается на карусели. Найдите значение силы упругости, действующей на человека при его движении в горизонтальной плоскости со скоростью 10 м/с по окружности радиусом 12 м.
Дано:
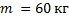
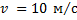
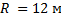
----------------
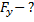
Решение:
Движение человека по окружности, лежащей в горизонтальной плоскости, происходит под действием равнодействующей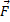 сил тяжести
сил тяжести 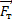 и упругости
и упругости 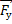 . Вектор
. Вектор 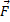 лежит в горизонтальной плоскости и направлен к центру окружности (см. рисунок).
лежит в горизонтальной плоскости и направлен к центру окружности (см. рисунок).
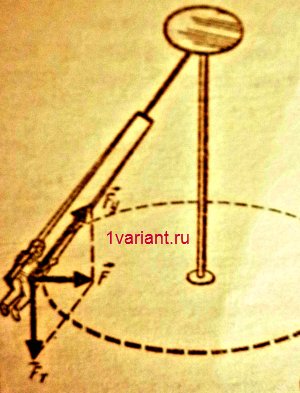
По второму закону Ньютона модуль равнодействующей равен
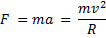
Так как вектор 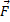 перпендикулярен вектору
перпендикулярен вектору 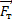 , то вектор
, то вектор 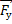 является гипотенузой в прямоугольном треугольнике с катетами
является гипотенузой в прямоугольном треугольнике с катетами 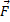 и
и 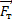 . Модуль вектора силы упругости равен
. Модуль вектора силы упругости равен
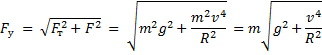
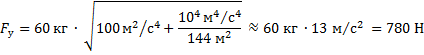
Ответ: 780 Н.
ЗАДАЧА 4.
 Велосипедист массой 80 кг движется со скоростью 10 м/с по вогнутому мосту, траектория его движения является дугой окружности радиусом 20 м. Определите силу упругости, действующую на велосипедиста в нижней точке моста.
Велосипедист массой 80 кг движется со скоростью 10 м/с по вогнутому мосту, траектория его движения является дугой окружности радиусом 20 м. Определите силу упругости, действующую на велосипедиста в нижней точке моста.
Дано:
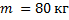
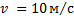
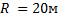
------------------
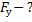
Решение:
Движение велосипедиста по дуге окружности является движением с центростремительным ускорением 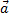 , равным по модулю
, равным по модулю  .
.
В нижней точке моста вектор центростремительного ускорения направлен вертикально вверх. Это ускорение по второму закону Ньютона определяется равнодействующей векторов силы тяжести 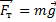 , направленной вертикально вниз, и силы упругости
, направленной вертикально вниз, и силы упругости 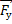 , действующей со стороны моста и направленной вертикально вверх (см. рисунок):
, действующей со стороны моста и направленной вертикально вверх (см. рисунок):
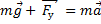
Направим ось OY вертикально вверх и запишем это уравнение в проекциях на эту ось:
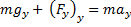
Проекции векторов 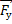 и
и 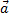 на эту ось положительны, а проекция вектора
на эту ось положительны, а проекция вектора 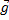 отрицательна, поэтому уравнение для модулей сил имеет вид:
отрицательна, поэтому уравнение для модулей сил имеет вид:
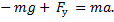
Отсюда получаем формулу для вычисления модуля силы упругости 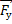 :
:
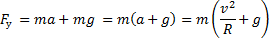
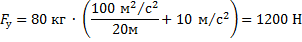
Ответ: 1200 Н.
ЗАДАЧА 5.
Труба массой 100 кг лежит на двух горизонтальных опорах. Длина трубы 6 м, одна опора находится у конца трубы, вторая – на расстоянии 1 м от второго конца трубы. Определите силы реакции опор.
Решение:
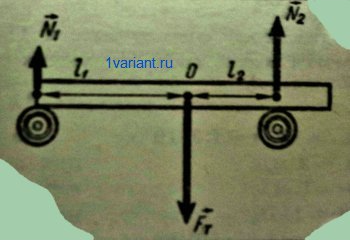
Изобразим все действующие на трубу силы (см. рисунок). Сила тяжести 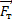 направлена вертикально вниз и приложена к центру масс трубы, находящемуся на равных расстояниях от концов трубы. Силы реакции опор
направлена вертикально вниз и приложена к центру масс трубы, находящемуся на равных расстояниях от концов трубы. Силы реакции опор 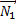 и
и 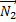 направлены вертикально вверх. Так как труба не движется поступательно, геометрическая сумма векторов сил, действующих на трубу, равна нулю:
направлены вертикально вверх. Так как труба не движется поступательно, геометрическая сумма векторов сил, действующих на трубу, равна нулю:
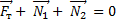
Направим ось OY вертикально вверх. Тогда для проекций сил на эту ось имеем равенство
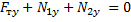
а для модулей - 
Так как труба не вращается, алгебраическая сумма моментов всех сил, действующих на нее, равна нулю для любой оси вращения. Выберем в качестве оси вращения горизонтальную прямую, проходящую через центр масс трубы перпендикулярно плоскости чертежа. На основании правила моментов запишем равенство
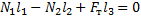
Так как вектор 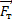 силы тяжести проходит через ось вращения
силы тяжести проходит через ось вращения 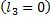 , момент этой силы равен нулю. Вектор силы
, момент этой силы равен нулю. Вектор силы 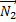 реакции опоры создает вращение против часовой стрелки, поэтому вращательный момент этой силы взят с отрицательным знаком. Таким образом, для решения задачи мы получили систему из двух уравнений:
реакции опоры создает вращение против часовой стрелки, поэтому вращательный момент этой силы взят с отрицательным знаком. Таким образом, для решения задачи мы получили систему из двух уравнений:
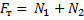
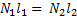
Решаем эту систему:
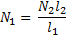
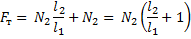
 По условию задачи
По условию задачи 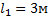 ,
, 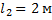 , поэтому
, поэтому
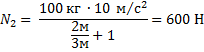
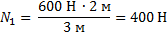
Ответ: 600 Н и 400 Н.
ЗАДАЧА 6.
Тепловоз массой 130 тонн приближается со скоростью 2 м/с к неподвижному составу массой 1170 тонн. С какой скоростью будет двигаться состав после сцепления с тепловозом ?
Дано:
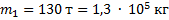
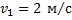
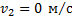

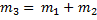
------------------------------------------------
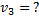
Решение:
По закону сохранения импульса проекции вектора полного импульса системы из тепловоза и состава на ось координат, направленную по вектору скорости, до сцепления и после сцепления одинаковы:
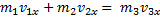
Так как состав был неподвижным, векторы скорости 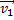 тепловоза до сцепления и скорости
тепловоза до сцепления и скорости 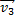 тепловоза вместе с составом после сцепления параллельны, и проекции векторов
тепловоза вместе с составом после сцепления параллельны, и проекции векторов 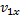 и
и 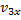 можно заменить их модулями:
можно заменить их модулями:

отсюда скорость 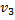 тепловоза и состава после сцепления равна
тепловоза и состава после сцепления равна
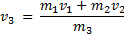
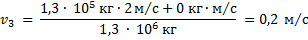
Ответ: 0,2 м/с.
ЗАДАЧА 7.
Человек массой 70 кг спускается по лестнице длиной 20 м, расположенной под углом 300 к горизонтальной плоскости. Найдите работу силы тяжести.
Дано:
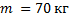
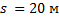
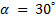
_______________
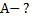
Решение:
Работа силы тяжести равна произведению модуля вектора силы 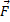 на модуль вектора перемещения
на модуль вектора перемещения 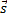 и косинус угла α между вектором
и косинус угла α между вектором 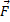 силы и вектором
силы и вектором 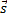 перемещения:
перемещения:
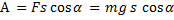
Угол α равен 60°, поэтому работа равна:
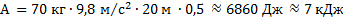
Ответ: 7 кДж.
ЗАДАЧА 8.
Вычислите работу силы упругости при изменении деформации пружины жесткостью 200 Н/м от 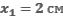 до
до  .
.
Дано:
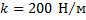
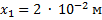
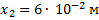
_______________
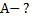
Решение:
По закону Гука проекция вектора силы упругости на ось OX, направленную по вектору перемещения конца пружины при ее деформации, равна
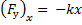
Так как сила упругости изменяется пропорционально деформации, то для вычисления работы можно найти среднее значение ее проекции при изменении деформации пружины от 2 см до 6 см:
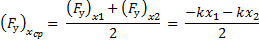
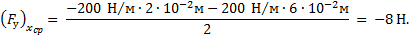
Работа силы упругости равна произведению модуля среднего значения силы на модуль перемещения и косинус угла между этими векторами:
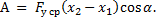
При растяжении пружины вектор силы упругости направлен противоположно вектору перемещения, поэтому угол α между ними равен 180° , а 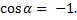 Тогда работа силы упругости будет равна
Тогда работа силы упругости будет равна
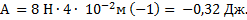
Работа силы упругости может быть найдена и по изменению потенциальной энергии пружины:
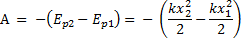
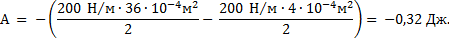
Ответ: - 0,32 Дж.
ЗАДАЧА 9.
Кран поднимает груз массой 2 т на высоту 24 м за 2 минуты. Найдите механическую мощность. Силами трения пренебречь.
Дано:
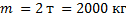
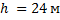
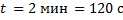
____________________

Решение:
Механическая мощность равна
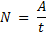
Механическая работа A внешних сил при подъеме груза равна изменению его потенциальной энергии:
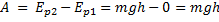
Поэтому механическая мощность равна:

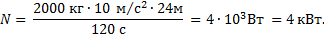 Ответ: 4 кВт.
Ответ: 4 кВт.
ЗАДАЧА 10.
Самолет Ил-62 имеет четыре двигателя, сила тяги каждого 103 кН. Какова полезная мощность двигателей при полете самолета со скоростью 864 км/ч ?
Дано:

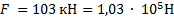
________________________

Решение:
Полезная мощность N двигателей равна отношению механической работы А ко времени t:
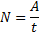
Механическая работа при совпадении направлений векторов силы 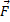 и перемещения
и перемещения 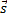 равна:
равна:
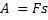
Отсюда для механической мощности имеем:
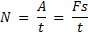
Так как при равномерном прямолинейном движении 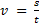 , то
, то 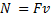 .
.
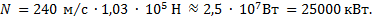
Ответ: 25000 кВт.
ЗАДАЧА 11.
На высоте 2,2 м от поверхности Земли мяч имел скорость 10 м/с. С какой скоростью будет двигаться мяч у поверхности Земли ? Сопротивлением воздуха пренебречь, ускорение свободного падения принять равным 10 м/с2.
Дано:
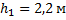
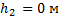
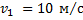

____________
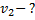
Решение:
Хотя в условии задачи не указаны направление вектора скорости мяча и масса мяча, задача имеет однозначное решение. Так как на мяч действует только сила тяготения со стороны Земли, к замкнутой системе «Земля – мяч» применим закон сохранения механической энергии.
Согласно этому закону полная механическая энергия системы «Земля – мяч» остается неизменной, а изменение кинетической энергии мяча равно изменению его потенциальной энергии, взятому с противоположным знаком:
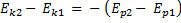
Обозначив массу мяча m, получим:
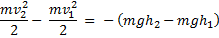
Разделим обе части равенства на m и умножим на 2:
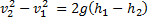
Отсюда скорость 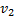 мяча у поверхности Земли равна
мяча у поверхности Земли равна
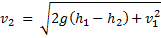
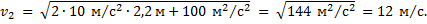
Ответ: 12 м/с.
ЗАДАЧА 12.
Саяно-Шушенская гидроэлектростанция вырабатывает 23,5 млрд. кВт*ч электроэнергии в год. Сколько воды проходит за год через гидротурбины станции? Высота плотины – 222 м. Считать, что потенциальная энергия воды полностью превращается в электрическую энергию.
Дано:
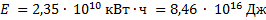
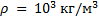
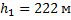
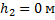
_______________________________________
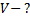
Решение:
По закону сохранения энергии электроэнергия, вырабатываемая гидроэлектростанцией, получается за счет превращения кинетической энергии движущейся воды в энергию электрического тока. Кинетическая энергия воды в свою очередь получается в результате превращения потенциальной энергии воды у вершины плотины в кинетическую у основания плотины. Если не учитывать потери, то вся выработанная гидроэлектростанцией энергия Е равна изменению потенциальной энергии 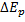 воды, прошедшей через гидроагрегаты станции, взятому с противоположным знаком:
воды, прошедшей через гидроагрегаты станции, взятому с противоположным знаком:
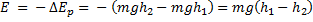
Массу m воды выразим через ее объём V и плотность 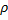 :
:

Из равенств (1) и (2) найдем выражение для объёма воды, прошедшей через гидроагрегаты станции:
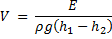
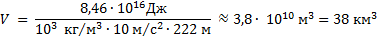
Ответ: 38 км3.
ЗАДАЧА 13.
Определите минимальное значение тормозного пути автомобиля, начавшего торможение на горизонтальном участке шоссе при скорости движения 20 м/с. Коэффициент трения равен 0,5.
Дано:
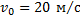
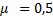
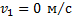
____________
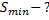
Решение:
Тормозной путь автомобиля будет иметь минимальное значение при максимальном значении силы трения. Модуль максимального значения силы трения равен:
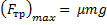
Вектор силы трения 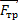 при торможении направлен противоположно векторам скорости
при торможении направлен противоположно векторам скорости 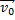 и перемещения
и перемещения 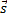 .
.
При прямолинейном равноускоренном движении проекция перемещения Sx автомобиля на ось, параллельную вектору скорости 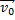 автомобиля, равна:
автомобиля, равна:
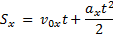
Переходя к модулям величин, получаем уравнение:
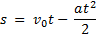
Значение времени t можно найти из условия:
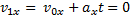
или
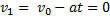
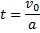
Тогда для модуля перемещения S получаем:
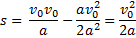
Так как
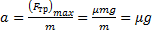
то

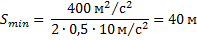
Тот же результат можно получить на основе использования теоремы о кинетической энергии:
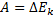
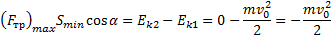
Так как вектор силы трения направлен противоположно вектору перемещения, угол 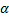 равен
равен 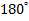 ,
, 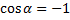 . Поэтому
. Поэтому
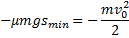
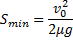
Ответ: 40 м.
ЗАДАЧА 14.
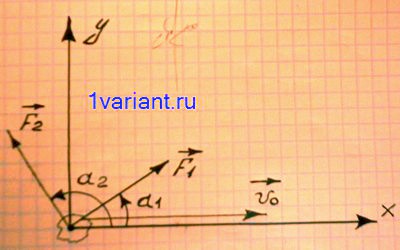
На тело массой 2 кг действуют силы 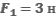 и
и 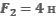 под углами
под углами 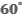 и
и 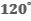 к начальной скорости
к начальной скорости  . Найти ускорение тела, его скорость и перемещение к концу 10-й секунды движения.
. Найти ускорение тела, его скорость и перемещение к концу 10-й секунды движения.
Решение:
Так как силы, действующие на тело, постоянны, то и ускорение будет постоянным
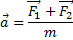
Выбирая оси координат вдоль 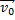 (ось x) и перпендикулярно к
(ось x) и перпендикулярно к 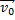 (ось y), получим
(ось y), получим
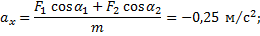
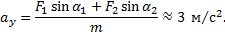
Так как 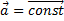 , то
, то
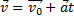
или
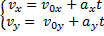
и так как
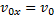 и
и 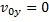 , то
, то
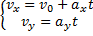
Поскольку 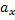 и
и 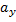 уже найдены, то, подставляя их значения, получим
уже найдены, то, подставляя их значения, получим
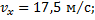
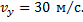
Аналогично найдём и перемещение
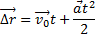
или в проекциях на оси
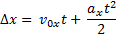

В силу того, что 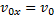 и
и 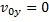 , имеем
, имеем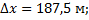
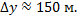
ЭЛЕКТРОДИНАМИКА.
РЕШЕНИЕ ЗАДАЧ.
ЗАДАЧА 1.
Точечные электрические заряды q1,q2 и q3 находятся в вершинах прямоугольника. Определите силу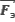 , с которой действует на заряд q3 электрическое поле зарядов q1 и q2. Расстояние между зарядами q3 и q1 равно 1 см, между зарядами q3 и q2 – 3 см;
, с которой действует на заряд q3 электрическое поле зарядов q1 и q2. Расстояние между зарядами q3 и q1 равно 1 см, между зарядами q3 и q2 – 3 см; 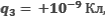
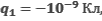
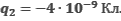
Дано:
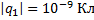
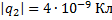
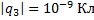
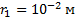
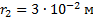
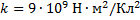
_____________________
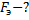
Решение:
Сила 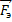 , с которой действует электрическое поле зарядов q1 и q2 на заряд q3, находится как сумма сил
, с которой действует электрическое поле зарядов q1 и q2 на заряд q3, находится как сумма сил 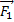 и
и 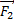 , действующих со стороны зарядов q1 и q2 на заряд q3 (см. рисунок).
, действующих со стороны зарядов q1 и q2 на заряд q3 (см. рисунок).
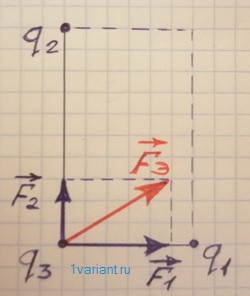
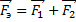
Так как угол между векторами 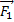 и
и 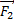 равен
равен 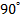 , то модуль вектора
, то модуль вектора 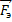 можно найти, используя теорему Пифагора:
можно найти, используя теорему Пифагора:
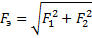 , где
, где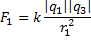
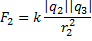
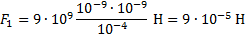
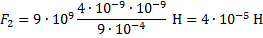
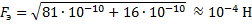
Ответ: 10-4 Н
ЗАДАЧА 2.
Вычислите напряженность электрического поля в точке А, находящейся на прямой, проходящей через два точечных электрических заряда 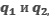 расположенных в точках В и С.
расположенных в точках В и С. 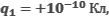
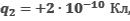
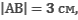
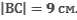
Рассмотреть все возможные случаи расположения точки А по отношению к точкам В и С.
Дано:
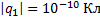
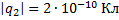
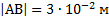
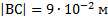
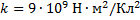 ___________________
___________________
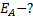
Решение:
Напряженность электрического поля 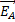 в точке А равна
в точке А равна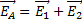
где 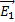 и
и 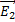 – напряженности полей, создаваемых в точке А зарядами q1 и q2. Модули напряженностей
– напряженности полей, создаваемых в точке А зарядами q1 и q2. Модули напряженностей 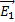 и
и 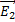 соответственно равны:
соответственно равны:
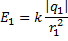
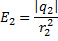
где  ,
, 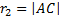
По условию задачи возможны два случая. В первом случае точка А находится между точками В и С (рисунок 1).

Тогда
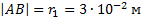
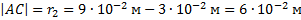 и
и
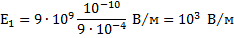
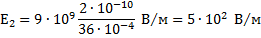
Векторы 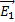 и
и 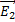 направлены противоположно, по модулю вектор
направлены противоположно, по модулю вектор 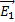 больше вектора
больше вектора 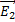 .
.
Поэтому вектор 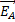 направлен от В к А и модуль его равен
направлен от В к А и модуль его равен
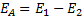
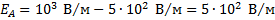
Во втором случае точки А и С находятся по разные стороны от точки В (рисунок 2).

В этом случае:

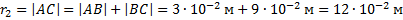
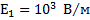
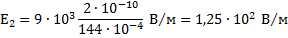
Векторы 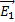 и
и 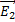 направлены в одну сторону:
направлены в одну сторону:
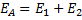
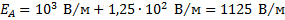
Ответ: 500 В/м или 1125 В/м.
ЗАДАЧА 3.
На каком расстоянии от маленького заряженного шара напряженность электрического поля в воде с диэлектрической проницаемостью 81 будет такой же, как в вакууме на расстоянии 18 см от центра шара?
Дано:
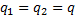
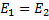
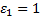
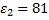
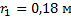
____________
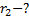
Решение:
Так как напряженность поля одинакова:
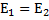 , то
, то 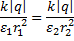
Отсюда расстояние 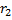 равно:
равно: 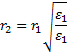
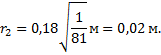
Ответ: 0,02 м.
ЗАДАЧА 4.
Ускоряющее напряжение в электроннолучевой трубке равно 1,5 кВ, расстояние от отклоняющих пластин до экрана – 30 см. На какое расстояние сместится пятно на экране осциллографа при подаче на отклоняющие пластины напряжения 20 В? Расстояние между пластинами – 0,5 см, длина пластин – 2,5 см.
Дано:
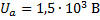
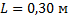
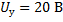
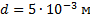
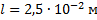
_______________
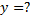
Решение:
Выберем систему координат с осью OX, направленную вдоль оси трубки, по направлению вектора 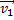 скорости электронов до входа в пространство между отклоняющими пластинами. Ось OY выберем направленной противоположно вектору напряженности электрического поля между отклоняющимися пластинами (см. рисунок).
скорости электронов до входа в пространство между отклоняющими пластинами. Ось OY выберем направленной противоположно вектору напряженности электрического поля между отклоняющимися пластинами (см. рисунок).
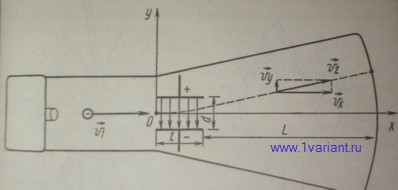
Пренебрегая малым смещением электронов между пластинами, отклонение у электронноголуча можно найти, зная проекцию скорости электрона на ось OY после прохождения между отклоняющими пластинами и время 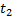 движения электрона от отклоняющих пластин до экрана:
движения электрона от отклоняющих пластин до экрана:
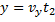
Время 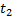 равно
равно 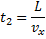
Проекцию скорости электрона на ось OY можно найти по проекции ускорения 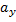 и времени
и времени  движения электрона между пластинами:
движения электрона между пластинами:
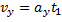
где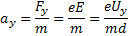
(e – заряд электрона, m – его масса),
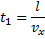
Так как кинетическая энергия электрона равна работе сил ускоряющего электрического поля, проекцию скорости электрона 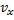 можно найти из выражения:
можно найти из выражения:
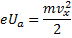
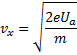
Используя все вышеприведенные выражения, получим:
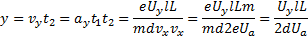
Подставляя данные из условия задачи, находим смещение луча:
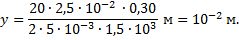
Ответ: 10-2 м.
ЗАДАЧА 5.
Внутрь незаряженной металлической сферы на изолирующей подставке вносится заряженный металлический шарик. Будет ли существовать электрическое поле внутри сферы и вне ее?
Решение:
Возможны два случая.
1.Шарик касается внутренней поверхности сферы, при этом все свободные электрические заряды с него переходят на сферу и взаимным отталкиванием вытесняются на ее внешнюю поверхность. Распределение свободных зарядов на поверхности проводящего тела устанавливается такое, при котором напряженность электрического поля внутри проводника равна нулю. Если напряженность поля равна нулю, в проводнике и внутри сферы нет свободных зарядов, то напряженность поля внутри сферы равна нулю. Вне сферы электрическое поле создается свободными зарядами, находящимися на внешней поверхности сферы (рисунок 1).
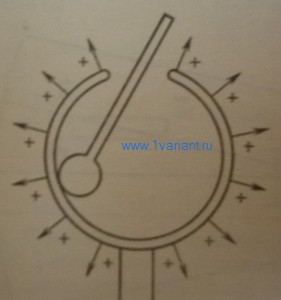
2.Заряженный шарик внесен внутрь металлической сферы и не касается ее внутренней поверхности (рисунок 2), тогда электрическое поле заряженного шарика приводит в движение свободные заряды в металлической сфере. На внутренней поверхности сферы сосредоточиваются электрические заряды противоположного знака, на внешней поверхности – того же знака, что и на заряженном шарике. Электрическое поле существует как внутри сферы, так и вне ее. Между внутренней и внешней поверхностями сферы напряженность электрического поля равна нулю.

ЗАДАЧА 6.
Как изменятся напряженность электрического поля, напряжение и энергия заряженного плоского воздушного конденсатора при увеличении расстояния между пластинами в два раза?
Решение:
Возможны два случая.
1. Если конденсатор заряжен до напряжения U и отключен от источника тока, то при раздвижении пластин неизменной величиной является электрический заряд q на его пластинах. При увеличении расстояния d между пластинами электроемкость конденсатора
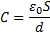
уменьшается в два раза. Поэтому напряжение 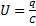 увеличивается в два раза.
увеличивается в два раза.
Напряженность Е поля между пластинами
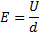
при одинаковом увеличении напряжения U и расстояния d остается постоянной.
Энергия конденсатора равна
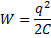
Так как заряд q постоянен, а электроемкость С уменьшается в два раза, то энергия увеличивается в два раза. Увеличение энергии в два раза происходит за счет работы внешних сил, совершаемой при раздвижении пластин конденсатора.
2. Если конденсатор подключен к источнику тока, напряжение между его пластинами при их раздвигании остается постоянным. Напряженность поля при постоянном напряжении U и увеличении в два раза расстояния d уменьшается в два раза.
Энергия конденсатора равна

При постоянном напряжении U и уменьшении в два раза электроемкости C энергия уменьшается в два раза. Уменьшение энергии заряженного конденсатора происходит потому, что с уменьшением электроемкости при раздвигании пластин электрический заряд на его пластинах убывает в два раза, т.е. конденсатор разряжается.
ЗАДАЧА 7.
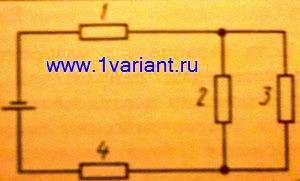
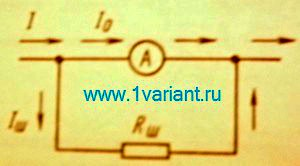
Определите общее электрическое сопротивление четырех проводников – 1, 2, 3, 4 – с электрическими сопротивлениями 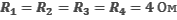 , соединенных между собой по схеме, представленной на рисунке.
, соединенных между собой по схеме, представленной на рисунке.
Дано:
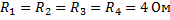
________________________
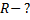
Решение:
Проводники 2 и 3 соединены параллельно между собой и последовательно с проводниками 1 и 4.
 Для определения общего электрического сопротивления цепи необходимо найти общее сопротивление
Для определения общего электрического сопротивления цепи необходимо найти общее сопротивление 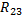 параллельно включенных проводников 2 и 3 и затем сумму электрических сопротивлений последовательно включенных проводников:
параллельно включенных проводников 2 и 3 и затем сумму электрических сопротивлений последовательно включенных проводников:
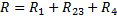
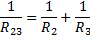
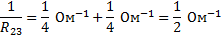
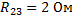
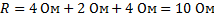 Ответ: 10 Ом.
Ответ: 10 Ом.
ЗАДАЧА 8.
Параллельно амперметру включается шунт – резистор с электрическим сопротивлением  в n раз меньшим внутреннего сопротивления
в n раз меньшим внутреннего сопротивления 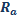 прибора. Во сколько раз при этом изменяются показания прибора?
прибора. Во сколько раз при этом изменяются показания прибора?
Дано:
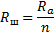
_________
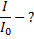
При решении задачи используем формулы параллельного соединения: напряжение на шунте и амперметре имеет одно и то же значение U, а сила тока I в неразветвленной цепи равна сумме сил токов 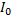 через амперметр и
через амперметр и 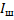 через шунт:
через шунт:

Отсюда следует, что
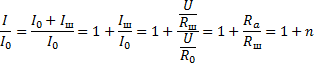
Сила тока I в неразветвленной цепи в 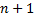 раз больше силы тока
раз больше силы тока 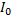 , регистрируемой амперметром.
, регистрируемой амперметром.
ЗАДАЧА 9.
Последовательно с вольтметром, внутреннее сопротивление которого 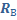 , включен дополнительный резистор с электрическим сопротивлением
, включен дополнительный резистор с электрическим сопротивлением 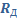 , в n раз большим сопротивления вольтметра. Во сколько раз при этом расширились пределы измерения напряжения вольтметром?
, в n раз большим сопротивления вольтметра. Во сколько раз при этом расширились пределы измерения напряжения вольтметром?
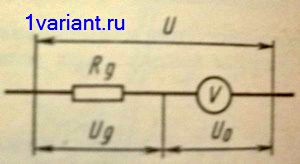
Решение:
Если вольтметр с внутренним сопротивлением 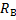 предназначен для измерения напряжений до максимального значения
предназначен для измерения напряжений до максимального значения 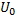 , то при включении последовательно с вольтметром дополнительного резистора с электрическим сопротивлением
, то при включении последовательно с вольтметром дополнительного резистора с электрическим сопротивлением 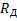 , измеряемое напряжение U будет равно сумме напряжений
, измеряемое напряжение U будет равно сумме напряжений 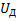 на дополнительном резисторе и
на дополнительном резисторе и 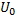 на вольтметре:
на вольтметре:
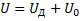
Отсюда следует:
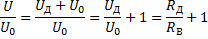
По условию отношение
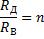
поэтому
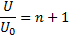
Мы получили, что при включении последовательно с вольтметром дополнительного резистора, сопротивление которого в n раз превосходит сопротивление вольтметра, показания вольтметра уменьшатся в n+1 раз. В результате вольтметром с дополнительным резистором можно измерить напряжение в 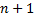 раз большее, чем тем же вольтметром без дополнительного резистора.
раз большее, чем тем же вольтметром без дополнительного резистора.
ЗАДАЧА 10.
Сколько времени потребуется для нагревания воды массой 1 кг от начальной температуры  до кипения в электрическом чайнике с электрическим нагревателем мощностью 1 кВт, если его КПД равен 90%? Какова сила тока в электрической спирали нагревательного элемента, если напряжение равно 220 В?
до кипения в электрическом чайнике с электрическим нагревателем мощностью 1 кВт, если его КПД равен 90%? Какова сила тока в электрической спирали нагревательного элемента, если напряжение равно 220 В?
Дано:
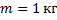
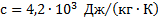
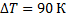
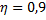
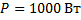
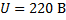
______________________
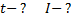
Решение:
Количество теплоты, необходимое для нагревания воды в чайнике, определяется по формуле
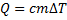
Оно связано с мощностью 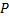 нагревателя, его КПД и временем t выражением
нагревателя, его КПД и временем t выражением

Отсюда
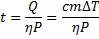
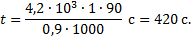
Для нахождения силы тока выразим электрическую мощность через силу тока 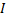 и напряжение
и напряжение 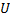 :
:
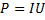
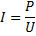
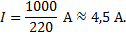
Ответ: 420 с; 4,5 А.
ЗАДАЧА 11.
С какой силой действует магнитное поле с индукцией 1,5 Тл на проводник длиной 30 см, расположенный перпендикулярно вектору индукции? Сила тока в проводнике равна 2 А.
Дано:
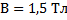
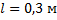
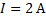
__________
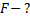
Решение:
Так как проводник расположен перпендикулярно вектору индукции 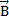 ,то модуль силы Ампера определяется выражением
,то модуль силы Ампера определяется выражением
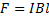
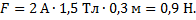
Ответ: 0,9 Н.
ЗАДАЧА 12.
При равномерном изменении силы тока от 1 до 6 А за 0,1 с в катушке возникает ЭДС самоиндукции 50 В. Какова индуктивность катушки?
Дано:
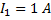
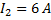
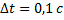
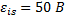
___________
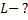
Для решения задачи воспользуемся формулой, выражающей связь ЭДС самоиндукции с индуктивностью катушки 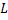 и скоростью изменения силы тока:
и скоростью изменения силы тока:
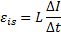
Откуда
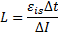
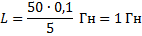
Ответ: 1 Гн
ЗАДАЧА 13.
Магнит вдвигается северным полюсом в металлическое кольцо. Притягивается при этом кольцо или отталкивается? Какое направление имеет индукционный ток в кольце?
Решение:
Для решения задачи необходимо воспользоваться правилом Ленца. Согласно правилу Ленца, индукционный ток в контуре имеет такое направление, что создаваемое этим током магнитное поле препятствует тем изменениям магнитного потока через контур, которые вызывают появление индукционного тока. Направление вектора индукции магнитного поля, вызывающего появление ЭДС индукции, показано на рисунке. При вдвигании магнита магнитный поток возрастает. По правилу Ленца индукционный ток в кольце должен создать магнитное поле, вектор индукции которого имеет противоположное направление. Такому направлению вектора индукции соответствует направление тока в кольце, указанное на рисунке стрелкой (определено при помощи правила буравчика).
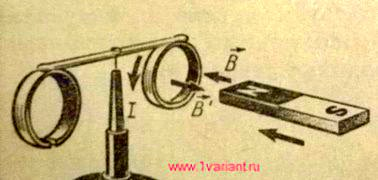
Так как векторы индукции магнитного поля постоянного магнита и кольца с током направлены навстречу друг другу, кольцо с током эквивалентно магниту, повернутому навстречу постоянному магниту одноименным полюсом. Кольцо будет отталкиваться.
КОЛЕБАНИЯ И ВОЛНЫ.
РЕШЕНИЕ ЗАДАЧ.
ЗАДАЧА 1.
Поршень в цилиндре двигателя проходит расстояние 66 мм между крайними положениями за  . Принимая, что движение поршня происходит по гармоническому закону, определите максимальную скорость поршня.
. Принимая, что движение поршня происходит по гармоническому закону, определите максимальную скорость поршня.
Решение:
Расстояние 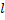 между крайними положениями поршня равно удвоенной амплитуде
между крайними положениями поршня равно удвоенной амплитуде 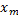 колебаний:
колебаний:
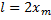
Отсюда амплитуда колебаний равна

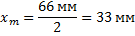
Расстояние между крайними положениями поршень проходит за половину периода, поэтому период 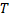 колебаний равен
колебаний равен
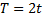
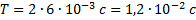
Циклическая частота колебаний поршня равна


Амплитуда изменений скорости 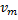 при гармонических колебаниях связана с амплитудой колебаний координаты
при гармонических колебаниях связана с амплитудой колебаний координаты 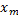 и циклической частотой
и циклической частотой 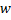 выражением
выражением
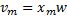
Отсюда максимальная скорость поршня равна
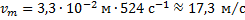 Ответ: 17,3 м/с.
Ответ: 17,3 м/с.
ЗАДАЧА 2.
Длина маятника, демонстрирующего вращение Земли, равна 98 м. С какой скоростью проходит маятник положение равновесия при амплитуде колебаний 2 м?
Решение:
Так как амплитуда колебаний маятника и размеры тела на подвесе малы по сравнению с длиной подвеса, его колебания можно считать гармоническими и для описания колебаний применить формулу периода колебаний математического маятника:
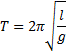
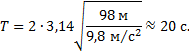
Амплитуду изменений скорости 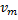 выразим через амплитуду колебаний координаты
выразим через амплитуду колебаний координаты 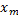 и циклическую частоту
и циклическую частоту 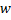 :
:
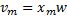
Где 
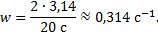
Отсюда амплитуда колебаний скорости маятника равна
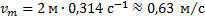 Ответ: 0,63 м/с.
Ответ: 0,63 м/с.
ЗАДАЧА 3.
При подвешивании груза массой 1 кг стальная пружина в положении равновесия удлинилась на 1 см. С каким периодом будет совершать колебания этот груз на пружине после смещения его по вертикали из положения равновесия?
Решение:
Под действием силы упругости пружины тело массой m совершает гармонические колебания с периодом, определяемым по формуле
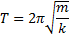
где k – жёсткость пружины.
Жёсткость пружины можно найти по ее удлинению под действием силы тяжести груза массой m. По закону Гука
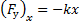
Для модуля силы упругости в положении равновесия выполняется равенство
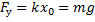
следовательно, 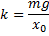
Подставляем полученное выражение в формулу для вычисления периода колебаний:
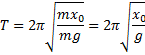
Отсюда период колебаний равен 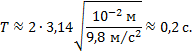
Мы получили, что для решения задачи достаточно было знать только удлинение пружины в положении равновесия, так как масса тела не входит в окончательную расчетную формулу.
Ответ: 0,2 с.
ЗАДАЧА 4.
Какую электроемкость должен иметь конденсатор для того, чтобы состоящий из этого конденсатора и катушки индуктивностью 10 мГн колебательный контур радиоприемника был настроен на волну 1000 м?
Решение:
Для настройки приемника на заданную волну частота собственных колебаний в контуре должна быть равной частоте колебаний в принимаемой волне.
Частота собственных колебаний в контуре определяется из формулы Томсона:
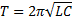
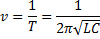
Частота v колебаний связана с длиной волны 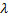 и скоростью ее распространения
и скоростью ее распространения 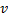 формулой
формулой
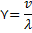
Отсюда для вычисления электроемкости конденсатора получаем выражение:
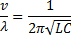
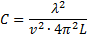
Скорость 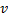 распространения радиоволн равна примерно
распространения радиоволн равна примерно 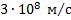 , поэтому получаем:
, поэтому получаем:
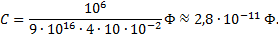
Ответ: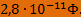
ЗАДАЧА 5.
Человек находится на расстоянии 2 м от плоского зеркала. На сколько изменится расстояние между человеком и его изображением, если человек приблизится к зеркалу на 1 м?
Решение:
Изображение в плоском зеркале находится за зеркалом на расстоянии, равном расстоянию от предмета до зеркала. При приближении человека к зеркалу на 1м изображение приближается к зеркалу также на 1м, а расстояние между человеком и его изображением уменьшается на 2 м.
Ответ: уменьшится на 2 м.
ЗАДАЧА 6.
При наблюдении через дифракционную решетку красный край спектра виден на расстоянии 3,5 см от середины щели в экране. Расстояние от дифракционной решетки до экрана – 50 см, период решетки – 10-2 мм. Определите длину волны красного цвета.

Дано:
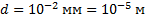
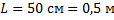
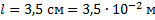
______________________
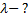
Решение:
Запишем условие первого максимума:
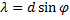
Так как угол 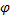 очень мал, справедливо равенство (см. рисунок)
очень мал, справедливо равенство (см. рисунок)
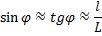
Тогда для определения длины волны получим выражение
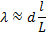
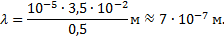
Ответ: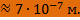
ЗАДАЧА 7.
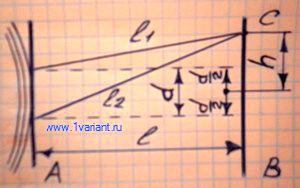
На экран А (см. рисунок) от точечного источника, находящегося от него на большом расстоянии, падает свет с длиной волны 560 нм. В экране имеются две параллельные щели на расстоянии 10-4 м одна от другой. Определите расстояние между двумя соседними полосами интерференционных максимумов, наблюдаемых на экране В, расположенном параллельно экрану А на расстоянии 1 м от него.
Дано:

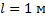
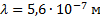
_______________
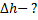
Решение:
В произвольной точке С экрана В (см. рисунок) будет наблюдаться интерференционный максимум при выполнении условия:
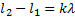
Из рисунка видно, что
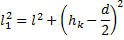
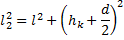
Отсюда следует, что
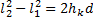
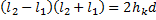
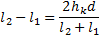
В случае, когда 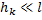 , можно считать справедливым приближенное равенство
, можно считать справедливым приближенное равенство 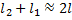 .
.
Тогда
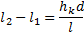
Приравнивая два выражения для разности 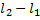 , получаем:
, получаем:
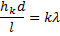
откуда
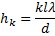
Искомое расстояние 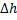 между соседними интерференционными полосами найдём так:
между соседними интерференционными полосами найдём так:
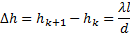
Подставляя значения величин, получаем:
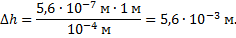
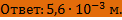
ЗАДАЧА 8.
Лампа находится на расстоянии 2 м от экрана. На каком расстоянии от лампы нужно поставить собирающую линзу с фокусным расстоянием 0,4 м, для того чтобы получить на экране увеличенное изображение лампы?
Дано:
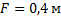
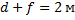
____________
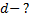
Решение:
В формулу линзы
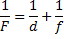
подставим 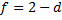
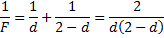

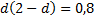
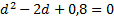
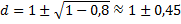
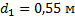
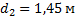
Получению увеличенного изображения соответствует значение 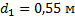 .
.
Ответ: 0,55 м.
ЗАДАЧА 9.
На каком расстоянии от собирающей линзы с фокусным расстоянием 10 см нужно поставить предмет, для того чтобы получить действительное изображение с увеличением в 10 раз?
Дано:
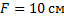
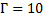
__________
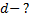
Решение:
Увеличение 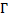 равно
равно  , отсюда
, отсюда 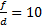 ; следовательно,
; следовательно, 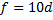 .
.
Воспользуемся формулой тонкой линзы:
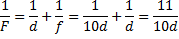

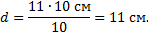 Ответ: 11 см.
Ответ: 11 см.
ЗАДАЧА 10.
На рисунке 1 показана главная оптическая ось линзы 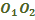 . Линза дает изображение точки А в точке В. Найдите построением хода лучей положение оптического центра линзы и ее главных фокусов.
. Линза дает изображение точки А в точке В. Найдите построением хода лучей положение оптического центра линзы и ее главных фокусов.

Решение:
При прохождении через линзу один из всех лучей, выходящих из точки А, попадает в точку В по прямой без изменения направления распространения. Это луч, проходящий через оптический центр линзы. Следовательно, оптический центр лежит на главной оптической оси 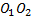 и на прямой АВ, поэтому точка
и на прямой АВ, поэтому точка 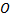 пересечения прямой АВ и главной оптической оси
пересечения прямой АВ и главной оптической оси 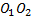 и является оптическим центром линзы
и является оптическим центром линзы 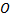 (рисунок 2).
(рисунок 2).
Чтобы найти положения главных фокусов линзы, проведем через точку  прямую, перпендикулярную главной оптической оси и отмечающую положение линзы.
прямую, перпендикулярную главной оптической оси и отмечающую положение линзы.
Так как предмет и его изображение находятся по разные стороны от линзы, изображение действительное. Следовательно, линза собирающая.
Для нахождения положения главного фокуса собирающей линзы выберем луч, идущий из точки А параллельно главной оптической оси. Этот луч после преломления в линзе попадает в точку В, как и все остальные лучи, выходящие из точки А. Вместе с тем луч, параллельный главной оптической оси, при выходе из линзы проходит через ее главный фокус, лежащий на главной оптической оси. Следовательно, точка пересечения этого луча с главной оптической осью является главным фокусом линзы. Второй главный фокус расположен на главной оптической оси по другую сторону от оптического центра на таком же расстоянии, как и первый.
 Задача
Задача
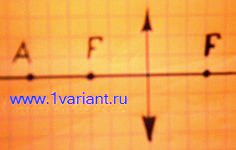
Найдите построением хода лучей изображение точки А, лежащей на главной оптической оси собирающей линзы. Положение главных фокусов линзы указано на рисунке 1.
Решение:
Для нахождения изображения точки А выберем произвольно направленный луч АВ. Чтобы найти направление его распространения после прохождения линзы, проведем через оптический центр линзы побочную ось, параллельную лучу АВ (рисунок 2). Лучи, параллельные побочной оси, собираются в одну точку, находящуюся в фокальной плоскости линзы. Отметим на рисунке положение этой плоскости прямой FE.
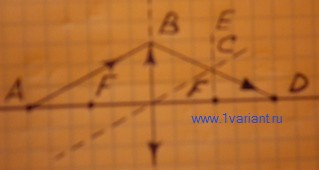
Луч АВ после преломления в линзе проходит через точку С пересечения побочной оси с фокальной плоскостью. Прямая, проходящая через точки В и С, отмечает направление распространения луча АВ после преломления в линзе. Точка D пересечения луча с главной оптической осью и является изображением точки А.
ЗАДАЧА 12.
Определите оптическую силу D системы из двух тонких линз с оптической силой D1 и D2.
Решение:
Представим себе, что точечный источник света помещается в главном фокусе первой линзы. Если вторая линза расположена вплотную к первой, то параллельный пучок света, выходящий из первой линзы, собирается в главном фокусе второй линзы.
Применяя формулу линзы для системы из двух линз, получаем:
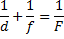
где F – фокусное расстояние системы из двух линз.
Так как в данном случае 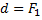 и
и 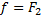 , то
, то
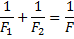
или

Мы получили, что оптическая сила системы из двух тонких линз равна сумме оптических сил этих линз.
| ЗАДАЧА 13. Расстояние от оптического центра глаза до сетчатки 18,3 мм. Человек пользуется очками с оптической силой +2 дптр для чтения газеты на расстоянии 25 см. На каком расстоянии от глаз он вынужден держать газету для чтения без очков? Оптическая сила нормального глаза 58,5 дптр. Дано: 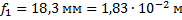
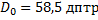
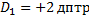
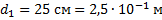
__________________________ 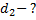
Решение: Расстояние 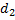 до предмета связано с расстоянием до предмета связано с расстоянием 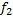 до изображения и фокусным расстоянием до изображения и фокусным расстоянием 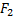 или оптической силой или оптической силой 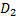 формулой линзы: формулой линзы: 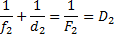
Из формулы линзы получаем: 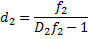
Так как изображение в первом и втором случае должно быть на сетчатке глаза, выполняется равенство: 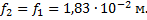
Оптическая сила глаза с очками равна оптической силе нормального глаза  и равна сумме оптической силы и равна сумме оптической силы 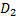 глаза без очков и оптической силы глаза без очков и оптической силы 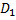 линзы очков: линзы очков: 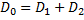
Отсюда 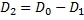
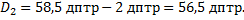
Расстояние до газеты получается равным: 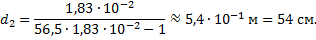
Ответ: 54 см.
|
ЗАДАЧА 14.
Определите увеличение оптической системы микроскопа, составленной из двух короткофокусных линз. Фокусное расстояние объектива 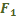 , фокусное расстояние окуляра
, фокусное расстояние окуляра 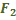 . Расстояние
. Расстояние 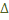 между главными фокусами объектива и окуляра значительно больше фокусного расстояния объектива.
между главными фокусами объектива и окуляра значительно больше фокусного расстояния объектива.
Решение:
Увеличение микроскопа 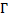 равно произведению увеличения объектива
равно произведению увеличения объектива 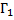 на увеличение окуляра
на увеличение окуляра 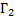 :
:
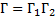
Увеличение объектива 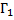 равно
равно
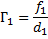
Рассматриваемый предмет расположен вблизи главного фокуса объектива, поэтому 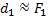 .
.
Чтобы можно было использовать вторую линзу – окуляр – в качестве лупы, действительное изображение предмета, даваемое объективом, должно оказаться вблизи фокальной плоскости второй линзы (см. рисунок).
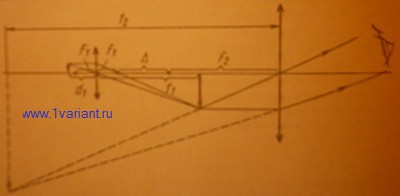
Поэтому приблизительно выполняется равенство
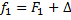
Так как 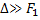 , то
, то 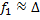 . Поэтому для увеличения
. Поэтому для увеличения 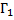 объектива получим:
объектива получим:
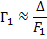
Увеличение окуляра как лупы равно
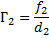
Так как расстояние 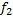 равно расстоянию наилучшего зрения глаза, а
равно расстоянию наилучшего зрения глаза, а 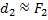 , то окончательно для определения увеличения
, то окончательно для определения увеличения 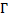 микроскопа получим выражение
микроскопа получим выражение
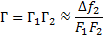
(здесь 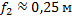 ).
).
КВАНТОВАЯ ФИЗИКА.
РЕШЕНИЕ ЗАДАЧ.
ЗАДАЧА 1.
Определите красную границу фотоэффекта для металла с работой выхода 2 эВ.
Дано:
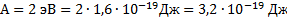
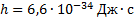
_________________________________________
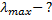
Решение:
Из уравнения Эйнштейна (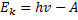 ) для фотоэффекта при условии
) для фотоэффекта при условии 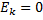 имеем:
имеем:
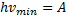
Частота 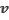 света связана с его скоростью
света связана с его скоростью  и длиной волны
и длиной волны 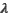 выражением
выражением
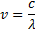
Из этих двух формул получаем:
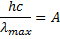
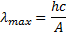
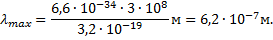
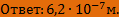
ЗАДАЧА 2.
Найдите максимальную скорость электронов, освобождаемых при фотоэффекте светом с длиной волны 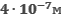 с поверхности материала с работой выхода 1,9 эВ.
с поверхности материала с работой выхода 1,9 эВ.
Дано:

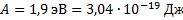
__________________________
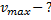
Решение:
Для решения задачи воспользуемся уравнением Эйнштейна для фотоэффекта 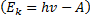 , подставив в него выражение
, подставив в него выражение
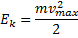
для максимальной кинетической энергии электронов.
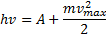
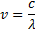
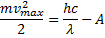
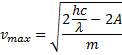
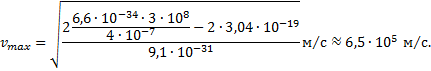
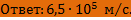
ЗАДАЧА 3.
Определите работу выхода электрона с поверхности фотокатода и красную границу фотоэффекта, если при облучении фотоэлемента светом с частотой 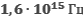 фототок прекращается при запирающем напряжении
фототок прекращается при запирающем напряжении 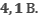
Дано:
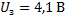
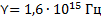
_______________
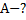
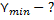
Решение:
Используем условие запирания фототока:
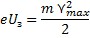
С учетом этого условия уравнение Эйнштейна для фотоэффекта будет иметь вид:
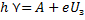
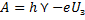
Определим красную границу фотоэффекта:
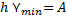
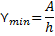
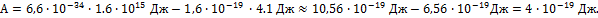
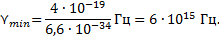
| ЗАДАЧА 4. При бомбардировке электронами атомы ртути переходят в возбужденное состояние, если энергия электронов равна 4,9 эВ или превышает это значение. Рассчитайте длину волны света, испускаемого атомом ртути при переходе из первого возбужденного состояния в нормальное. Дано: 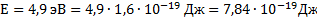
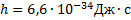
______________________________________________ 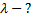
Решение: Используем связь между энергией фотона и частотой: 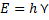 отсюда 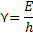
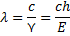
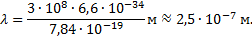 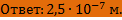
|
ЗАДАЧА 5.
Вычислите энергию связи ядра атома дейтерия.
Дано:
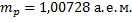
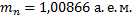
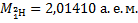
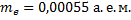
____________________
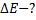
Решение:
Энергия связи ядра равна
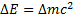
где 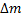 – разность суммы масс свободных частиц, входящих в состав ядра, и массы ядра, с – скорость света в вакууме. Для нахождения разности масс отыскиваем в справочнике по физике сведения о массах протона
– разность суммы масс свободных частиц, входящих в состав ядра, и массы ядра, с – скорость света в вакууме. Для нахождения разности масс отыскиваем в справочнике по физике сведения о массах протона 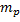 , нейтрона
, нейтрона 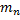 , электрона
, электрона 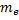 и атома дейтерия
и атома дейтерия 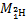 . Для нахождения массы ядра дейтерия
. Для нахождения массы ядра дейтерия 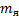 необходимо вычесть из массы атома дейтерия массу электрона, находящегося на его оболочке:
необходимо вычесть из массы атома дейтерия массу электрона, находящегося на его оболочке:
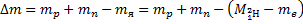
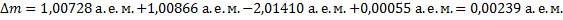
Но 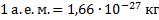 , поэтому
, поэтому
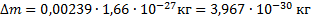
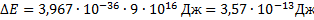
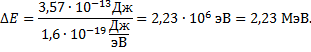
ЗАДАЧА 6.
Вычислите энергетический выход ядерной реакции
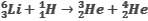
Решение:
Для вычисления энергетического выхода ядерной реакции необходимо найти разность масс частиц, вступающих в реакцию, и частиц – продуктов реакции. В реакции участвуют атомные ядра, но в справочных таблицах обычно даются сведения лишь о массах атомов. Можно найти массу каждого атомного ядра вычитанием массы электронов оболочки из массы атома. Можно поступить иначе. Если в уравнении ядерной реакции слева и справа пользоваться только массами атомов (т.е. массой атома водорода, а не массой протона слева, и массой атома гелия, а не массой альфа-частицы справа), то из-за одинаковости числа электронов в атомах, вступающих в реакцию, и в продуктах реакции их вычитание осуществляется автоматически при нахождении разности масс. Таким образом, для решения задачи можно воспользоваться сведениями из справочника о массах атомов.
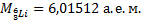
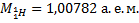
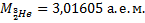
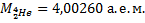
_____________________
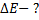
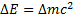

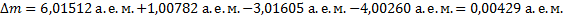
Вычислим энергетический выход при изменении массы на 1 а.е.м.:
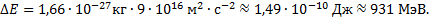
Выход ядерной реакции равен
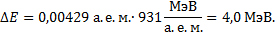
Ответ: 4,0 МэВ.
ЗАДАЧА 7.
При осуществлении термоядерной реакции синтеза ядра гелия из ядер изотопов водорода – дейтерия и трития – по схеме
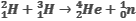
освобождается энергия 17,6 МэВ. Какая энергия освободится при синтезе 1 г гелия? Сколько каменного угля потребовалось бы сжечь для получения такой же энергии?
Дано:
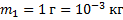
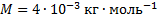
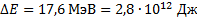
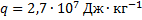
_____________________________
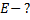
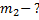
Решение:
Для нахождения энергии, выделяющейся при синтезе 1 г гелия, нужно умножить выход ядерной реакции 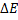 на число осуществленных реакций, равное числу атомов гелия
на число осуществленных реакций, равное числу атомов гелия 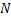 в 1 г:
в 1 г:
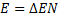
Число атомов гелия 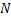 равно
равно
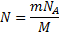 ;
; 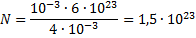
Поэтому для энергии 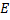 получим:
получим:
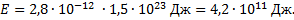
Из условия 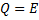 следует:
следует: 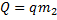 ;
; 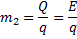
Отсюда масса каменного угля, при сжигании которого освобождается столько же энергии, сколько и при синтезе 1 г гелия, равна
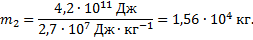
ЗАДАЧА 8.
Определите второй продукт ядерной реакции:

Решение:
Для определения второго продукта ядерной реакции необходимо использовать тот факт, что при осуществлении ядерных реакций число протонов и нейтронов остается неизменным. Отсюда следует, что сумма протонов в частицах, вступающих в реакцию, должна быть равна сумме протонов в частицах – продуктах реакции, а общее число нуклонов в левой части уравнения равно общему числу нуклонов в правой его части. Число протонов в частицах, вступивших в данную ядерную реакцию, равно 3. В ядре гелия 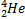 только два протона, следовательно, во втором продукте ядерной реакции содержится один протон. Таким образом, второй продукт ядерной реакции является одним из изотопов водорода. Найдем массовое число этого изотопа. Общее число нуклонов в ядрах, представленных в левой части уравнения, равно 7. В ядре гелия
только два протона, следовательно, во втором продукте ядерной реакции содержится один протон. Таким образом, второй продукт ядерной реакции является одним из изотопов водорода. Найдем массовое число этого изотопа. Общее число нуклонов в ядрах, представленных в левой части уравнения, равно 7. В ядре гелия 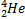 четыре нуклона, следовательно, на долю второго продукта ядерной реакции приходится три нуклона.
четыре нуклона, следовательно, на долю второго продукта ядерной реакции приходится три нуклона.
Таким образом, второй продукт ядерной реакции является изотопом водорода – тритием 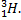
| ЗАДАЧА 9. Определите, какая частица участвует в осуществлении ядерной реакции: 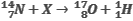
Решение: Воспользовавшись свойством сохранения числа протонов и общего числа нуклонов при осуществлении ядерных реакций, можно определить, что неизвестная частица X содержит два протона и состоит из четырех нуклонов. Следовательно, это ядро атома гелия 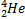 (альфа-частица). (альфа-частица).
|
ЗАДАЧА 10.
Фотон с длиной волны, соответствующей красной границе фотоэффекта, выбивает электрон из металлической пластинки (катода), помещенной в сосуд, из которого откачан воздух. Электрон разгоняется однородным электрическим полем напряженностью Е. Пролетев путь  , он приобретает скорость
, он приобретает скорость 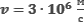 . Определите напряженность электрического поля? Релятивистские эффекты не учитывать.
. Определите напряженность электрического поля? Релятивистские эффекты не учитывать.
Решение:В данной задаче уравнение Эйнштейна имеет вид: 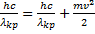
Отсюда следует, что начальная скорость вылетевшего электрона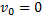
Формула, связывающая изменение кинетической энергии частицы с работой силы со стороны электрического поля: 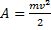
Работа силы связана с напряженностью поля и пройденным путем: 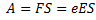
Отсюда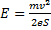
Ответ: 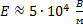
ЗАДАЧА 11.
Фотон с длиной волны, соответствующей красной границе фотоэффекта, выбивает электрон из металлической пластинки (катода), помещенной в сосуд, из которого откачан воздух. Электрон разгоняется однородным электрическим полем напряженностью Е. Пролетев путь 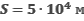 , он приобретает скорость
, он приобретает скорость 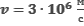 . Определите напряженность электрического поля. Релятивистские эффекты не учитывать.
. Определите напряженность электрического поля. Релятивистские эффекты не учитывать.
Решение:
В данной задаче уравнение Эйнштейна имеет вид:
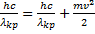
Отсюда следует, что начальная скорость вылетевшего электрона 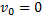 .
.
Формула, связывающая изменение кинетической энергии частицы с работой силы со стороны электрического поля: 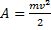 .
.
Работа силы связана с напряженностью поля и пройденным путем: 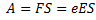 .
.
Отсюда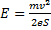
Ответ: 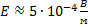
ЗАДАЧА 12.
При облучении металлической пластинки квантами света с энергией 3 эВ из нее выбиваются электроны, которые проходят ускоряющую разность потенциалов 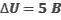 . Какова работа выхода
. Какова работа выхода 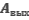 , если максимальная энергия ускоренных электронов
, если максимальная энергия ускоренных электронов 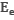 равна удвоенной энергии фотонов, выбивающих их из металла?
равна удвоенной энергии фотонов, выбивающих их из металла?
Решение:
Уравнение Эйнштейна для фотоэффекта:
 +
+ 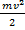
Энергия ускоренных электронов: 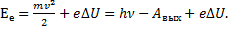
По условию: 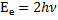 Отсюда:
Отсюда: 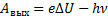 Ответ:
Ответ: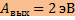
ЗАДАЧА 13.
При облучении металлической пластинки квантами света с энергией 3 эВ из нее выбиваются электроны, которые проходят ускоряющую разность потенциалов U. Работа выхода электронов из металла 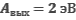 . Определите ускоряющую разность потенциалов U, если максимальная энергия ускоренных электронов
. Определите ускоряющую разность потенциалов U, если максимальная энергия ускоренных электронов 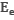 равна удвоенной энергии фотонов, выбивающих их из металла.
равна удвоенной энергии фотонов, выбивающих их из металла.
Решение:
Уравнение Эйнштейна для фотоэффекта: 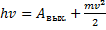
Энергия ускоренных электронов: 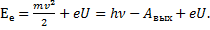
По условию:
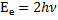
Отсюда: 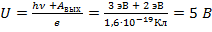 Ответ:
Ответ: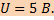
ЗАДАЧА 14.
Красная граница фотоэффекта для вещества фотокатода 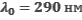 . При облучении катода светом с длиной волны
. При облучении катода светом с длиной волны 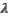 фототок прекращается при напряжении между анодом и катодом
фототок прекращается при напряжении между анодом и катодом 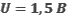 . Определите длину волны
. Определите длину волны 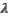 .
.
Решение:
Уравнение Эйнштейна для фотоэффекта: 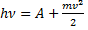
Условие связи красной границы фотоэффекта и работы выхода: 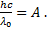
Выражение для запирающего напряжения — условие равенства максимальной кинетической энергии электрона и изменения его потенциальной энергии при перемещении в электростатическом поле:
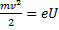
Решая систему уравнений: 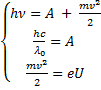
Получаем: 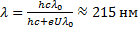 Ответ:
Ответ: 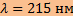
ЗАДАЧА 15.
Красная граница фотоэффекта для вещества фотокатода 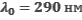 . Фотокатод облучают светом с длиной волны
. Фотокатод облучают светом с длиной волны 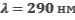 . При каком напряжении между анодом и катодом фототок прекращается?
. При каком напряжении между анодом и катодом фототок прекращается?
Решение:
Уравнение Эйнштейна для фотоэффекта: 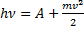
Условие связи красной границы фотоэффекта и работы выхода: 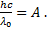
Выражение для запирающего напряжения — условие равенства максимальной кинетической энергии электрона и изменения его потенциальной энергии при перемещении в электростатическом поле:
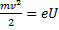
Решая систему уравнений: 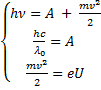
Получаем:
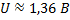
Ответ: 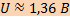







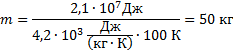 Ответ:
Ответ:  Отсюда
Отсюда При выборе оси абсцисс для отсчета значений температуры газа графики изотермических процессов представляют собой прямые, параллельные оси ординат (см. рисунок 2 и рисунок 3). Продолжение этих прямых до оси абсцисс пересекает ее в точках, соответствующих значениям температуры изотермического процесса. Ординаты верхней и нижней точек этих графиков определяются начальными и конечными значениями объема газа (рис. 2) и его давления (рис. 3).
При выборе оси абсцисс для отсчета значений температуры газа графики изотермических процессов представляют собой прямые, параллельные оси ординат (см. рисунок 2 и рисунок 3). Продолжение этих прямых до оси абсцисс пересекает ее в точках, соответствующих значениям температуры изотермического процесса. Ординаты верхней и нижней точек этих графиков определяются начальными и конечными значениями объема газа (рис. 2) и его давления (рис. 3).
 По известным начальным и конечным значениям давления и температуры построим в системе координат с осями p,T точки 1 и 2, соответствующие начальному и конечному состояниям газа. Зависимость давления p от температуры Т линейная, - следовательно, график изохорного процесса в координатных осях p,T является прямой, проходящей через точки 1 и 2 (рисунок 2).
По известным начальным и конечным значениям давления и температуры построим в системе координат с осями p,T точки 1 и 2, соответствующие начальному и конечному состояниям газа. Зависимость давления p от температуры Т линейная, - следовательно, график изохорного процесса в координатных осях p,T является прямой, проходящей через точки 1 и 2 (рисунок 2).

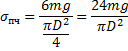
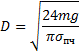
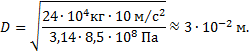


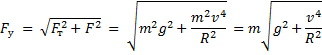
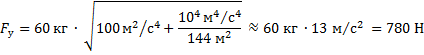
 Велосипедист массой 80 кг движется со скоростью 10 м/с по вогнутому мосту, траектория его движения является дугой окружности радиусом 20 м. Определите силу упругости, действующую на велосипедиста в нижней точке моста.
Велосипедист массой 80 кг движется со скоростью 10 м/с по вогнутому мосту, траектория его движения является дугой окружности радиусом 20 м. Определите силу упругости, действующую на велосипедиста в нижней точке моста.
 По условию задачи
По условию задачи 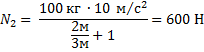




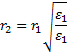
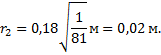

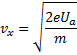



 Для определения общего электрического сопротивления цепи необходимо найти общее сопротивление
Для определения общего электрического сопротивления цепи необходимо найти общее сопротивление 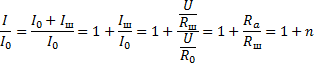


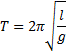
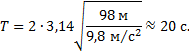
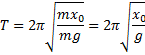
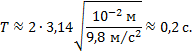




 Задача
Задача