Курсы для учителей от 800 ₽ (72 часа). Документы об окончании по почте БЕСПЛАТНО, комфортное обучение из дома

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до 19.05.2025

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Была в сети 10.02.2025 11:49

Затеева Валентина Павловна

учитель математики

70 лет

782 273

Местоположение

Россия, Энгельс

Специализация

Математика

Алгебра

Геометрия

Обо мне Блог Файлы Тесты Галерея Активность Награды

Задание 1-5. Вариант 5 ОГЭ 2022

Категория: Математика

12.07.2022 16:36

Задание 1-5. Вариант 5 ОГЭ 2022

Просмотр содержимого документа
«Задание 1-5. Вариант 5 ОГЭ 2022»

Задание 1-5. Вариант 5 ОГЭ 2022

В жилых домах установлены бытовые электросчётчики, которые фиксируют расход электроэнергии в киловатт-часах (кВт • ч). Учёт расхода электроэнергии может быть однотарифным, двухтарифным или трёхтарифным.

При однотарифном учёте стоимость 1 кВт • ч электроэнергии не меняется в течение суток. При двухтарифном и трёхтарифном учёте она различна в зависимости от времени суток (сутки разбиты на периоды, называемые тарифными зонами).

В таблице дана стоимость 1 кВт • ч электроэнергии в рублях в 2021 году.

	I полугодие 2021 г.	II полугодие 2021 г.
Однотарифный учёт	5,47	5,66
Двухтарифный учёт (распределение по двум тарифным зонам):
ночная зона Т2 (23:00-7:00)	2,13	2,32
дневная зона Т1 (7:00-23:00)	6,29	6,51
Трёхтарифный учёт (распределение по трём тарифным зонам):
ночная зона Т2 (23:00-7:00)	2,13	2,32
полупиковая зона Т3 (10:00-17:00; 21:00-23:00)	5,47	5,66
пиковая зона Т1 (7:00-10:00; 17:00-21:00)	6,57	6,79

В квартире у Николая Андреевича установлен трёхтарифный счётчик, и в 2021 году Николай Андреевич оплачивал электроэнергию по трёхтарифному учёту.

На рисунке точками показан расход электроэнергии в квартире Николая Андреевича по тарифным зонам за каждый месяц 2021 года. Для наглядности точки соединены линиями.

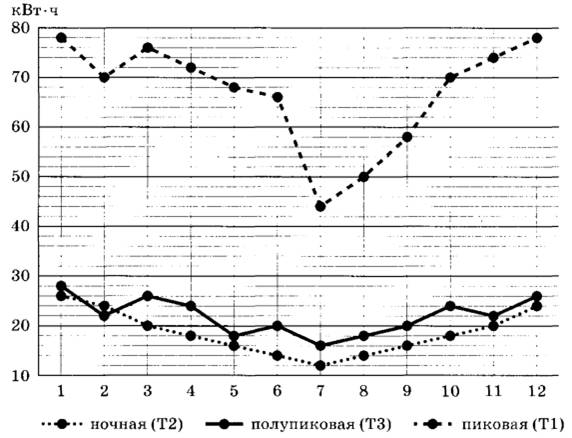
Задание 1. Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику расхода электроэнергии.

ПЕРИОДЫ

A) февраль — март

Б) апрель — май

B) май — июнь

Г) октябрь — ноябрь

ХАРАКТЕРИСТИКИ

1) расход уменьшился во всех трёх тарифных зонах, но больше всего — в полупиковой зоне

2) расход в ночной зоне увеличился на столько же, на сколько уменьшился расход в полупиковой зоне

3) расход в ночной зоне уменьшился, а в пиковой и полупиковой — увеличился

4) расход в пиковой и ночной зонах уменьшился одинаково

Решение.

А) расход в ночной зоне уменьшился, а в пиковой и полупиковой — увеличился – характеристика под номером 3;

Б) расход уменьшился во всех трёх тарифных зонах, но больше всего — в полупиковой зоне – характеристика под номером 1;

В) расход в пиковой и ночной зонах уменьшился одинаково – характеристика под номером 4;

Г) расход в ночной зоне увеличился на столько же, на сколько уменьшился расход в полупиковой зоне – характеристика под номером 2.

Ответ: 3142

Задание 2. В каком месяце I полугодия 2021 года общий расход электроэнергии был наибольшим? Запишите в ответ расход электроэнергии (в кВт • ч) в этом месяце.

Решение.

Из графика видно, что пиковое потребление в первом полугодии (первые 6 месяцев года) было зафиксировано в первый месяц и составило:

78 + 28 + 26 = 132 кВт • ч

Ответ: 132

Задание 3. Сколько рублей должен был заплатить Николай Андреевич за электроэнергию, израсходованную в марте?

Решение.

Март – это третий месяц года. По графику Николай Андреевич в этом месяце израсходовал:

Т1: 76 кВт • ч x 6,57 = 499,32 руб;

Т2: 20 кВт • ч x 2,13 = 42,6 руб;

Т3: 26 кВт • ч x 5,47 = 142,22 руб.

В сумме, имеем:

499,32 + 42,6 + 142,22 = 684,14 руб.

Ответ: 684,14

Задание 4. На сколько процентов больше заплатил бы Николай Андреевич за электроэнергию, израсходованную в феврале, если бы пользовался однотарифным учётом? Ответ округлите до десятых.

Решение.

Февраль – 2-й месяц. В этом месяце по трехтарифному плану он затратил:

70∙6,57 + 24∙2,13 + 22∙5,47 = 631,36 руб.

По однотарифному учету он потратил бы:

(70 + 24 + 22)∙5,47 = 634,52 руб.

Найдем отношение этих двух величин:

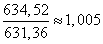
То есть, Николай Андреевич заплатил бы на 0,5% больше.

Ответ: 0,5

Задание 5. Сосед Николая Андреевича, Семён Семёнович, исходя из данных по расходу электроэнергии за 2021 год в своей квартире, рассчитал средний расход электроэнергии за месяц по тарифным зонам:

- ночная зона — 70 кВт • ч,

- полупиковая зона — 42 кВт • ч,

- пиковая зона — 188 кВт • ч.

Семён Семёнович предполагает, что в 2022 году средний расход электроэнергии будет таким же. Исходя из этого, выберите наиболее выгодный вариант учёта электроэнергии для Семёна Семёновича в 2022 году (однотарифный, двухтарифный или трёхтарифный). Считайте, что стоимость 1 кВт • ч электроэнергии будет такой же, как во II полугодии 2021, года. Оцените общие расходы Семёна Семёновича на оплату электроэнергии (в рублях) за 2022 год (по наиболее выгодному варианту учёта), если средний расход электроэнергии действительно будет таким же.

1) менее 5 тыс. руб.

2) от 5 тыс. руб. до 10 тыс. руб.

3) от 10 тыс. руб. до 15 тыс. руб.

4) от 15 тыс. руб. до 20 тыс. руб.

5) от 20 тыс. руб. до 25 тыс. руб.

6) более 25 тыс. руб.

В ответ запишите номер верного варианта оценки расходов.

Решение.

Для однотарифного плана имеем планируемый расход Семёна Семёновича в 2022 году:

(70+42+188) ∙ 5,66 = 1698 руб.

Для двухтарифного плана:

70∙2,32 + (42+188) ∙ 6,51 = 1659,7 руб.

Для трехтарифного плана:

70∙2,32 + 42∙5,66 + 188∙6,79 = 1676,64 руб.

Наиболее выгодный получается двухтарифный план составляет 1659,7 руб в месяц или:

1659,7 ∙ 12 = 19916,4 руб в год.

Попадает в диапазон пункта 4.

Ответ: 4

Задание 15. Прямая, параллельная стороне АС треугольника ABC, пересекает стороны АВ и ВС в точках М и N соответственно, АС = 44, MN = 24. Площадь треугольника ABC равна 121. Найдите площадь треугольника MNB.

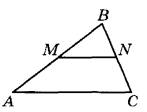
Решение.

Треугольники ABC и BMN подобны по трем углам с коэффициентом подобия AC:MN = 44:24 = 11:6. То есть, все линейные размеры большого треугольника ABC в 11/6 раз больше соответствующих размеров малого треугольника BMN. Следовательно, площадь малого треугольника MNB в 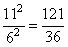раз меньше площади большого и равна:

Ответ: 36.

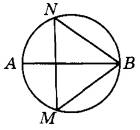
Задание 16. На окружности по разные стороны от диаметра АВ взяты точки М и N. Известно, что угол NBA = 36°. Найдите угол NMB. Ответ дайте в градусах.

Решение.

Угол NBA является вписанным углом и опирается на дугу AN, следовательно, градусная мера дуги AN равна:

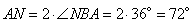Градусная мера дуги AB равна 180 градусов, так как это диаметр окружности, который делит круг в 360 градусов пополам. Тогда градусная мера дуги NB равна

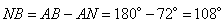На дугу NB опирается вписанный угол NMB, который равен половине градусной меры дуги NB:

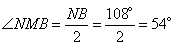Ответ: 54.

Задание 17. Диагонали АС и BD прямоугольника ABCD пересекаются в точке O, BO = 37, AB = 56. Найдите АС.

Решение.

Диагонали в прямоугольнике равны (AC=BD) и точкой пересечения O делятся пополам, то есть, BD=2BO, следовательно,

AC=2BO=2∙37=74.

Ответ: 74

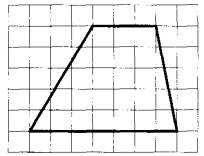
Задание 18. На клетчатой бумаге с размером клетки 1x1 изображена трапеция. Найдите длину её средней линии.

Решение.

Средняя линия трапеции равна полусумме ее оснований. Из рисунка видно, что основания трапеции, равны a = 3 и b = 7. Получаем длину средней линии:

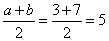
Ответ: 5

Задание 19. Какое из следующих утверждений верно?

1) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.

2) Сумма углов равнобедренного треугольника равна 180 градусам.

3) Диагонали ромба равны.

Решение.

1) Не обязательно, есть тупоугольные треугольники, у которых центр описанной окружности вне его.

2) Да, сумма углов любого треугольника, в том числе и равнобедренного, равна 180°.

3) Нет, диагонали ромба в общем случае не равны.

Ответ: 2.

Установите соответствие между графиками функций и формулами, которые их задают.

ГРАФИКИ

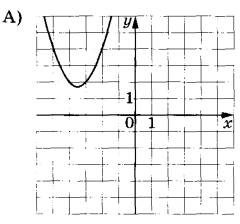
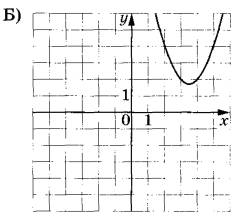
ФОРМУЛЫ

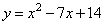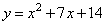1) ; 2) ; 3)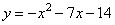

Решение.

Общая запись графика параболы имеет вид

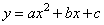
Если коэффициент a0, то ветви параболы направлены вверх, иначе – вниз. Далее, если парабола пересекает ось Oy в положительной области, то коэффициент c0, иначе c .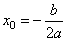

Подберем уравнения под изображенные графики параболы, используя приведенные правила.

1) Функция у = x^2 - 7x + 14 имеет коэффициент a0 и c0, значит, ветви параболы направлены вверх и она пересекает ось Oy в положительной области. Этому соответствуют два графика А и Б. Вычислим координату вершины: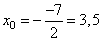 . Получаем график под буквой Б.

2) Функция у = x^2 + 7x + 14 имеет коэффициент a0 и c0, значит, ветви параболы направлены вверх и она пересекает ось Oy в положительной области. Этому соответствуют графики А и Б. Но, Б уже выбран, остается график А.

3) Функция у = -x^2 - 7х – 14 имеет коэффициент a

Ответ: 213.

Задание 12. Энергия заряженного конденсатора W (в Дж) вычисляется по формуле 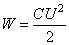, где C – ёмкость конденсатора (в Ф), a U — разность потенциалов на обкладках конденсатора (в В). Найдите энергию конденсатора (в Дж) ёмкостью Ф, если разность потенциалов на обкладках конденсатора равна 16 В.

Решение.

Подставим в формулу энергии конденсатора числовые значения, получим:

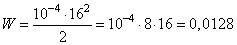Дж

Ответ: 0,0128

Задание 13. Укажите решение системы неравенств

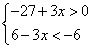
1) (4; +∞); 2) (4; 9); 3) (9; +∞); 4) (-∞; 9)

Решение.

Перепишем неравенство в виде:

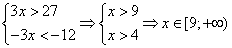
Ответ: 3

Задание 14. В амфитеатре 14 рядов. В первом ряду 20 мест, а в каждом следующем — на 3 места больше, чем в предыдущем. Сколько мест в десятом ряду амфитеатра?

Решение.

Нам нужно вычислить число мест в 10-м ряду. Учитывая, что каждый следующий ряд дает 3 дополнительных места, то для 10-го ряда, имеем:

20 + 9∙3 = 47 мест

Ответ: 47