Задание № 10. Практические задачи.
1. Уравнение процесса, в котором участвовал газ, записывается в виде pVa=const, где p (Па) — давление в газе, V — объем газа в кубических метрах, a — положительная константа. При каком наименьшем значении константы a уменьшение вдвое раз объем газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 4 раза?
Ответ: 2
2. Установка для демонстрации адиабатического сжатия представляет собой сосуд c поршнем, резко сжимающим газ. При этом объем и давление связаны соотношением pV1,4=const, где p (атм.) — давление в газе, V — объем газа в литрах. Изначально объем газа равен 1,6 л, а его давление равно одной атмосфере. В соответствии c техническими характеристиками поршень наcоcа выдерживает давление не более 128 атмосфер. Определите, до какого минимального объем можно сжать газ. Ответ выразите в литрах.
Ответ: 0,05
3. При адиабатическом процессе для идеального газа выполняется закон pVk=const, где p — давление в газе в паскалях, V — объем газа в кубических метрах. В ходе эксперимента c одноатомным идеальным газом (для него k=5/3) из начального состояния, в котором const=105Па∙м5, газ начинают сжимать. Какой наибольший объем V может занимать газ при давлениях p не ниже 3,2∙106 Па? Ответ выразите в кубических метрах.
Ответ: 0,125
4. При температуре 0°C рельс имеет длину 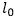 =10 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону l(t°)=l0(1+a∙t°), где a=1,2∙10-5 (°C)-1 — коэффициент теплового расширения t° — температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ выразите в градусах Цельсия.
=10 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону l(t°)=l0(1+a∙t°), где a=1,2∙10-5 (°C)-1 — коэффициент теплового расширения t° — температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ выразите в градусах Цельсия.
Ответ: 25
5. После дождя уровень воды в колодце может повыситься. Мальчик измеряет время падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле h=5t2, где h — расстояние в метрах, t — время падения в секундах. До дождя время падения камешков составляло 0,6 c. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 c? Ответ выразите в метрах.
Ответ: 1
6. Высота над землей подброшенного мяча меняется по закону h(t)=1,6+8t-5t2, где h — высота в метрах, t — время в секундах, прошедшее c момента броска. Сколько секунд мяч будет находиться на высоте не менее трех метров?
Ответ: 1,2
7. В боковой стенке высокого цилиндрического бака у самого дна закреплен кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нем, выраженная в метрах, меняется по закону H(t)=at2+bt+H0 , где H0 =4 м — начальный уровень воды, a=1/100 м/мин2, и b= -2/5 м/мин — постоянные, t — время в минутах, прошедшее c момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах.
Ответ: 20
8. В боковой стенке высокого цилиндрического бака у самого дна закреплен кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нем, выраженная в метрах, меняется по закону
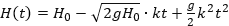
где t — время в секундах, прошедшее c момента открытия крана, H0=20 м — начальная высота столба воды, k=1/50 — отношение площадей поперечных сечений крана и бака, а g — ускорение свободного падения (считайте g =10м/с2). Через сколько секунд после открытия крана в баке останется четверть первоначального объем воды?
Ответ: 50
9. Камнеметательная машина выстреливает камни под некоторым острым углом к горизонту. Траектория полета камня описывается формулой y=ax2+bx, где b=1, a = -1/100 м-1 — постоянные параметры, x(м) — смещение камня по горизонтали, y(м) — высота камня над землей. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 8 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?
Ответ: 90
10. Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально и на исследуемом интервале температур определяется выражением T(t)=T0+bt+at2, где t — время в минутах, T0=1400 К, a= -10 К/мин2, b=200 К/мин. Известно, что при температуре нагревателя свыше 1760 К прибор может испортиться, поэтому его нужно отключать. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.
Ответ: 2
11. Для сматывания кабеля на заводе используют лебеду, которая равноускоренно наматывает кабель на катушку. Угол, на который поворачивается катушка, изменяется со временем по закону 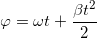 , где t — время в минутах, ω=20°/мин — начальная угловая скорость вращения катушки, а β=4°/мин2— угловое ускорение, c которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки φ достигнет 1200°. Определите время после начала работы лебеди, не позже которого рабочий должен проверить её работу. Ответ выразите в минутах.
, где t — время в минутах, ω=20°/мин — начальная угловая скорость вращения катушки, а β=4°/мин2— угловое ускорение, c которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки φ достигнет 1200°. Определите время после начала работы лебеди, не позже которого рабочий должен проверить её работу. Ответ выразите в минутах.
Ответ: 20
12. Деталью некоторого прибора является вращающаяся катушка. Она состоит из трех однородных цилиндров: центрального массой m=8 кг и радиуса R=10 см, и двух боковых c массами M=1 кг и c радиусами R+h. При этом момент инерции катушки относительно оси вращения, выражаемый в кг∙см2, дается формулой
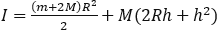
При каком максимальном значении h момент инерции катушки не превышает предельного значения 625 кг∙см2? Ответ выразите в сантиметрах.
Ответ: 5
13. На рисунке изображена схема вантового моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами. Введём систему координат: ось Oy направим вертикально вдоль одного из пилонов, а ось Ox направим вдоль полотна моста. В этой системе координат линия, по которой провисает цепь моста, имеет уравнение y=0,005x2-0,74x+25, где x и y измеряются в метрах. Найдите длину ванты, расположенной в 30 метрах от пилона. Ответ дайте в метрах.
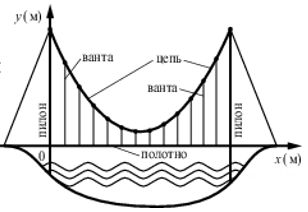
Ответ: 7,3
14. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза c главным фокусным расстоянием f=30 см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние d2 от линзы до экрана — в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение
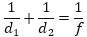
Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы ей изображение на экране было чётким. Ответ выразите в сантиметрах.
Ответ: 36
15. Перед отправкой тепловоз издал гудок c частотой f0 =440 Гц. Чуть позже, издал гудок, подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f больше первого: она изменяется по закону
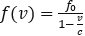
где c — скорость звука (в м/c). Человек, cтоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, c какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а c=315 м/c. Ответ выразите в м/c.
Ответ: 7
16. По закону Ома для полной цепи сила тока, измеряемая в амперах, равна 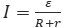 , где ε — ЭДC источника (в вольтах), r=1 Ом — его внутреннее сопротивление, R — сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 20% от силы тока короткого замыкания
, где ε — ЭДC источника (в вольтах), r=1 Ом — его внутреннее сопротивление, R — сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 20% от силы тока короткого замыкания 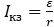 ? (Ответ выразите в омах.)
? (Ответ выразите в омах.)
Ответ: 4
17. Амплитуда колебаний маятника зависит от частоты вынуждающей силы, определяемой по формуле
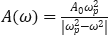
где ω — частота вынуждающей силы (в c-1), A0 — постоянный параметр, ωp=360 c-1 — резонансная частота. Найдите максимальную частоту ω, меньшую резонансной, для которой амплитуда колебаний превосходит величину A0 не более чем на 12,5%.
Ответ: 120
18. Коэффициент полезного действия (КПД) некоторого двигателя определяется
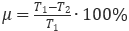
где T1 — температура нагревателя (в градусах Кельвина), T2 — температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя T1 КПД этого двигателя будет не меньше 15%, если температура холодильника T2 =340 К? Ответ выразите в градусах Кельвина.
Ответ: 400
19. Коэффициент полезного действия (КПД) кормозапарника равен отношению количества теплоты, затраченного на нагревание воды массой mВ (в килограммах) от температуры t1 до температуры t2 (в градусах Цельсия) к количеству теплоты, полученному от сжигания дров массы mдр кг. Он определяется формулой
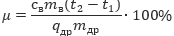
где св=4,2∙103 Дж/(кг К) — теплоёмкость воды, qдр=8,3∙106 Дж/кг — удельная теплота сгорания дров. Определите наименьшее количество дров, которое понадобится сжечь в кормозапарнике, чтобы нагреть m=83 кг воды от 10°C до кипения, если известно, что КПД кормозапарника не больше 21%. Ответ выразите в килограммах.
Ответ: 18
20. Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость спуска батискафа, выражаемая в м/c, определяется по формуле
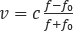
где c=1500 м/c — скорость звука в воде, f0 — частота испускаемых импульсов (в МГц), f — частота отраженного от дна сигнала, регистрируемая преемником (в МГц). Определите наибольшую возможную частоту отраженного сигнала f, если скорость погружения батискафа не должна превышать 2 м/c.
Ответ: 751
21. При сближении источника и приёмника звуковых сигналов движущихся в некоторой среде по прямой навстречу друг другу частота звукового сигнала, регистрируемого приемником, не совпадает c частотой исходного сигнала f0=150 Гц и определяется следующим выражением:
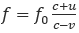
где с — скорость распространения сигнала в среде (в м/c), а u=10 м/c и v=15 м/c — скорости преемника и источника относительно среды соответственно. При какой максимальной скорости с (в м/с) распространения сигнала в среде частота сигнала в преемнике f будет не менее 160 Гц?
Ответ: 390
22. Если достаточно быстро вращать ведёрко c водой на верёвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведерка сила давления воды на дно не остаётся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила её давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления (в ньютонах) равна
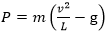
где m — масса воды в килограммах, v — скорость движения ветерка в м/c, L — длина веревки в метрах, g — ускорение свободного падения (считайте g=10м/с2). C какой наименьшей скоростью надо вращать ведёрко, чтобы вода не выливалась, если длина веревки равна 40 см? Ответ выразите в м/c.
Ответ: 2
23. При движении ракеты её видимая для неподвижного наблюдателя длина, измеряемая в метрах, сокращается по закону
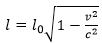
где l0=5 м — длина покоящейся ракеты, c=3∙105 км/c — скорость света, а v — скорость ракеты (в км/c). Какова должна быть минимальная скорость ракеты, чтобы ей наблюдаемая длина стала не более 4 м? Ответ выразите в км/c.
Ответ: 180000
24. Для определения эффективной температуры звезды используют закон Стефана–Больцмана, согласно которому мощность излучения нагретого тела P, измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвертой степени температуры: P=σST4, где σ=5,7∙10-8 — постоянная, площадь S измеряется в квадратных метрах, а температура T — в градусах Кельвина. Известно, что некоторая звезда имеет площадь 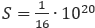 м2, а излучаемая ею мощность P не менее 9,12∙1025 Вт. Определите наименьшую возможную температуру этой звезды. Приведите ответ в градусах Кельвина.
м2, а излучаемая ею мощность P не менее 9,12∙1025 Вт. Определите наименьшую возможную температуру этой звезды. Приведите ответ в градусах Кельвина.
Ответ: 4000
25. Расстояние от наблюдателя, находящегося на высоте h над землей, до видимой им линии горизонта вычисляется по формуле 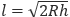 , где R=6400 км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. К пляжу ведет лестница, каждая ступенька которой имеет высоту 20 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 6,4 километров?
, где R=6400 км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. К пляжу ведет лестница, каждая ступенька которой имеет высоту 20 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 6,4 километров?
Ответ: 7
26. В ходе распада радиоактивного изотопа, его масса уменьшается по закону 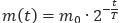 , где m0 — начальная масса изотопа, t (мин) — прошедшее от начального момента время, T — период полураспада в минутах. В лаборатории получили вещество, содержащее в начальный момент времени m0=40 мг изотопа Z, период полураспада которого T=10 мин. В течение скольких минут масса изотопа будет не меньше 5 мг?
, где m0 — начальная масса изотопа, t (мин) — прошедшее от начального момента время, T — период полураспада в минутах. В лаборатории получили вещество, содержащее в начальный момент времени m0=40 мг изотопа Z, период полураспада которого T=10 мин. В течение скольких минут масса изотопа будет не меньше 5 мг?
Ответ: 30
27. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: FA=αρgr3, где a=4,2 — постоянная, r — радиус аппарата в метрах, ρ=1000кг/м3 — плотность воды, а g — ускорение свободного падения (считайте g=10 Н/кг). Каким может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336 000 Н? Ответ выразите в метрах.
Ответ: 2
28. Водолазный колокол, содержащий в начальный момент времени v=3 моля воздуха объёмом V1=8 л, медленно опускают на дно водоема. При этом происходит изотермическое сжатие воздуха до конечного объема V2. Работа, совершаемая водой при сжатии воздуха, определяется выражением
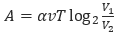
(Дж), где a=5,75 постоянная, а T=300 К — температура воздуха. Какой объем V2 (в литрах) станет занимать воздух, если при сжатии газа была совершена работа в 10350 Дж?
Ответ: 2
29. Находящийся в воде водолазный колокол, содержащий v=2 моля воздуха при давлении p1=1,5 атмосферы, медленно опускают на дно водоема. При этом происходит изотермическое сжатие воздуха. Работа, совершаемая водой при сжатии воздуха, определяется выражением
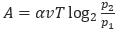
(Дж), где a=5,75 — постоянная, T=300 К — температура воздуха, p1(атм.) — начальное давление, а p2 (атм.) — конечное давление воздуха в колоколе. До какого наибольшего давления p2 можно сжать воздух в колоколе, если при сжатии воздуха совершается работа не более чем 6900 Дж? Ответ приведите в атмосферах.
Ответ: 6
30. Для обогрева помещения, температура в котором равна Tп=20°С, через радиатор отопления, пропускают горячую воду температурой Tв=60°С. Расход проходящей через трубу воды m=0,3 кг/c. Проходя по трубе расстояние x (м), вода охлаждается до температуры T(°C),прочем
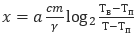
(м), где с =4200 Дж/кг°С — теплоёмкость воды, γ=21 Вт/м∙°С — коэффициент теплообмена, а a =0,7 — постоянная. До какой температуры (в градусах Цельсия) охладится вода, если длина трубы 84 м?
Ответ: 30
31. Ёмкость высоковольтного конденсатора в телевизоре C=2∙10-6 Ф. Параллельно c конденсатором подключен резистор c сопротивлением R=5∙106 Ом. Во время работы телевизора напряжение на конденсаторе U0=16 кв. После выключения телевизора напряжение на конденсаторе убывает до значения U (кв.) за время, определяемое выражением
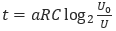
(c), где a =0,7 — постоянная. Определите (в киловольтах), наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 21 c?
Ответ: 2
32. Скорость колеблющегося на пружине груза меняется по закону v(t)=5sinπt (см/c), где t — время в секундах. Какую долю времени из первой секунды скорость движения превышала 2,5 см/c? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
Ответ: 0,67
33. Груз массой 0,08 кг колеблется на пружине со скоростью, меняющейся по закону v(t)=0,5sinπt, где t — время в секундах. Кинетическая энергия груза, измеряемая в джоулях, вычисляется по формуле
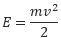
где m — масса груза (в кг), v — скорость груза (в м/c). Определите, какую долю времени из первой секунды после начала движения кинетическая энергия груза будет не менее 5∙10-3 Дж. Ответ выразите десятичной дробью, если нужно, округлите до сотых.
Ответ: 0,5
34. Небольшой мячик бросают под острым углом a к плоской горизонтальной поверхности земли. Расстояние, которое пролетает мячик, вычисляется по формуле
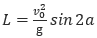
(м), где v0=20 м/c — начальная скорость мяча, а g — ускорение свободного падения (считайте g=10). При каком наименьшем значении угла (в градусах) мячик перелетит реку шириной 20 м?
Ответ:15
35. Небольшой мячик бросают под острым углом a к плоской горизонтальной поверхности земли. Максимальная высота полета мячика, выраженная в метрах, определяется формулой
где v0=20 м/c — начальная скорость мяча, а g — ускорение свободного падения (считайте g=10). При каком наименьшем значении угла a (в градусах) мячик пролетит над стеной высотой 4 м на расстоянии 1 м?
Ответ: 30
36. Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону U=U0 sin(ωt+φ), где t — время в секундах, амплитуда U0 =2, частота ω=120°/c, фаза φ= -30°. Датчик настроен так, что, если напряжение в нем не ниже чем 1 В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?
Ответ: 50
37. Некоторая компания продает свою продукцию по цене p=500 руб. за единицу, переменные затраты на производство одной единицы продукции составляют v=300 руб., постоянные расходы предприятия f=700000 руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле π(q)=q(p-v)-f. Определите наименьший месячный объем производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 300000 руб.
Ответ: 5000
38. Зависимость объем спроса q (тыс. руб.) на продукцию предприятия-монополиста от цены p (тыс. руб.) задается формулой q=100-10p. Выручка предприятия за месяц r (в тыс. руб.) вычисляется по формуле r(p)=q∙p. Определите наибольшую цену p, при которой месячная выручка r(p) составит не менее 240 тыс. руб. Ответ приведите в тыс. руб.
Ответ: 6
39. Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности In, оперативности Op, объективности публикаций Tr, а также качества сайта Q. Каждый отдельный показатель оценивается читателями по пятибалльной шкале целыми числами от -2 до 2. Аналитики, составляющие формулу рейтинга, считают, что объективность ценится втрое, а информативность публикаций — впятеро дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид
Если по всем четырем показателям какое-то издание получило одну и ту же оценку, то рейтинг должен совпадать с этой оценкой. Найдите число А, при котором это условие будет выполняться.
Ответ: 10
40. Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности In, оперативности Op, объективности публикаций Tr, а также качества сайта Q. Каждый отдельный показатель оценивается читателями по 5-балльной шкале целыми числами от 1 до 5. Аналитики, составляющие формулу рейтинга, считают, что объективность ценится втрое, а информативность публикаций — вдвое дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид
Каким должно быть число А, чтобы издание, у которого все оценки наибольшие, получило бы рейтинг 1?
Ответ: 35
41. Рейтинг R интернет-магазина вычисляется по формуле
где rпок — средняя оценка магазина покупателями (от 0 до 1), rэкс — оценка магазина экспертами (от 0 до 0,7) и K — число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина «Бета», если число покупателей, оставивших отзыв о магазине, равно 20, их средняя оценка равна 0,65, а оценка экспертов равна 0,37.
Ответ: 0,625
42. Рейтинг R интернет-магазина вычисляется по формуле
rэкс — средняя оценка, данная экспертами, rпок — средняя оценка, данная покупателями, K — число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 24, их средняя оценка равна 0,86, а оценка экспертов равна 0,11.
Ответ: 0,71
43. Мотоциклист, движущийся по городу со скоростью v0=57 км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением a =12 км/ч2. Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением

Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее, чем в 30 км от города. Ответ выразите в минутах.
Ответ: 30
44. Автомобиль, движущийся в начальный момент времени со скоростью v0=20 м/с, начал торможение с постоянным ускорением a=5 м/с2. За t – секунд после начала торможения он прошёл путь
Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 30 метров. Ответ выразите в секундах.
Ответ: 2
45. Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением a км/ч2. Скорость v вычисляется по формуле

где l — пройденный автомобилем путь. Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость 100 км/ч. Ответ выразите в км/ч2.
Ответ: 5000
46. Автомобиль, масса которого равна m=2160 кг, начинает двигаться с ускорением, которое в течение t секунд остаeтся неизменным, и проходит за это время путь S=500 метров. Значение силы (в ньютонах), приложенной в это время к автомобилю, равно

Определите наибольшее время после начала движения автомобиля, за которое он пройдeт указанный путь, если известно, что сила F, приложенная к автомобилю, не меньше 2400 Н. Ответ выразите в секундах.
Ответ: 30
47. Для поддержания навеса планируется использовать цилиндрическую колонну. Давление P (в паскалях), оказываемое навесом и колонной на опору, определяется по формуле

где m=1200 кг – общая масса навеса и колонны, D – диаметр колонны (в метрах). Считая ускорение свободного падения g=10 м/с2, а π=3, определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 400 000 Па. Ответ выразите в метрах.
Ответ: 0,2
48. Деталью некоторого прибора является квадратная рамка с намотанным на неe проводом, через который пропущен постоянный ток. Рамка помещена в однородное магнитное поле так, что она может вращаться. Момент силы Ампера, стремящейся повернуть рамку, (в Нм) определяется формулой  , где I=2A – сила тока в рамке, B=310-3 Тл – значение индукции магнитного поля, l=0,5 м – размер рамки, N=1000 – число витков провода в рамке, a – острый угол между перпендикуляром к рамке и вектором индукции. При каком наименьшем значении угла a (в градусах) рамка может начать вращаться, если для этого нужно, чтобы раскручивающий момент Mбыл не меньше 0,75 Нм?
, где I=2A – сила тока в рамке, B=310-3 Тл – значение индукции магнитного поля, l=0,5 м – размер рамки, N=1000 – число витков провода в рамке, a – острый угол между перпендикуляром к рамке и вектором индукции. При каком наименьшем значении угла a (в градусах) рамка может начать вращаться, если для этого нужно, чтобы раскручивающий момент Mбыл не меньше 0,75 Нм?
Ответ: 30°
49. Очень лёгкий заряженный металлический шарик зарядом q=210-6Кл скатывается по гладкой наклонной плоскости. В момент, когда его скорость составляет v=5 м/с, на него начинает действовать постоянное магнитное поле, вектор индукции B которого лежит в той же плоскости и составляет угол a с направлением движения шарика. Значение индукции поля B=410-3 Тл. При этом на шарик действует сила Лоренца, равная Fл =qvBsin α (Н) и направленная вверх перпендикулярно плоскости. При каком наименьшем значении угла aϵ [0°; 180°] шарик оторвётся от поверхности, если для этого нужно, чтобы сила Fл была не менее чем 210-8 Н? Ответ дайте в градусах.
Ответ: 30°
50. Плоский замкнутый контур площадью S=0,5 м2 находится в магнитном поле, индукция которого равномерно возрастает. При этом согласно закону электромагнитной индукции Фарадея, в контуре появляется ЭДС индукции, значение которой, выраженное в вольтах, определяется формулой εi =aScos α, где α – острый угол между направлением магнитного поля и перпендикуляром к контуру, a=410-4Тл/с – постоянная, S – площадь замкнутого контура, находящегося в магнитном поле (в м). При каком минимальном угле α (в градусах) ЭДС индукции не будет превышать 10-4 В?
Ответ: 60°
51. Два тела массой m = 2 кг каждое, движутся с одинаковой скоростью v = 10 м/с под углом 2α друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении вычисляется по формуле Q = mv2sin2α. Под каким наименьшим углом 2α (в градусах) должны двигаться тела, чтобы в результате соударения выделилось не менее 50 джоулей?
Ответ: 60°
52. Катер должен пересечь реку шириной L=100 м со скоростью течения u=0,5 м/с так, чтобы причалить точно напротив места отправления. Он может двигаться с разными скоростями, при этом время в пути, измеряемое в секундах, определяется выражением

где a – острый угол, задающий направление его движения (отсчитывается от берега). Под каким минимальным углом a (в градусах) нужно плыть, чтобы время в пути было не больше 200 с?
Ответ: 45°
53. Скейтбордист прыгает на стоящую на рельсах платформу, со скоростью v=3 м/с под острым углом a к рельсам. От толчка платформа начинает ехать со скоростью

(м/с), где m=80 кг – масса скейтбордиста со скейтом, а M=400 кг – масса платформы. Под каким максимальным углом a (в градусах) нужно прыгать, чтобы разогнать платформу не менее чем до 0,25 м/с?
Ответ: 60°
54. Опорные башмаки шагающего экскаватора, имеющего массу m=1260 тонн, представляют собой две пустотелые балки длиной l=18 метров и шириной s метров каждая. Давление экскаватора на почву, выражаемое в килопаскалях, определяется формулой

где m – масса экскаватора (в тоннах), l – длина балок в метрах, s – ширина балок в метрах, g – ускорение свободного падения (считайте g=10 м/с2). Определите наименьшую возможную ширину опорных балок, если известно, что давление p не должно превышать 140 кПа. Ответ выразите в метрах.
Ответ: 2,5
55. При нормальном падении света с длиной волны λ=400 нм на дифракционную решётку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол φ (отсчитываемый от перпендикуляра к решётке), под которым наблюдается максимум, и номер максимума k связаны соотношением dsin φ=kλ. Под каким минимальным углом φ (в градусах) можно наблюдать второй максимум на решётке с периодом, не превосходящим 1600 нм?
Ответ: 30°
















