Россия, Энгельс
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 19.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 10.02.2025 11:49
Затеева Валентина Павловна
учитель математики
70 лет
782 273
12 
Местоположение
Специализация
Задание 15-19 вариант 4 ОГЭ 2022 из 36 вариантов
Категория:
Математика
08.07.2022 23:53
Просмотр содержимого документа
«Задание 15-19 вариант 4 ОГЭ 2022 из 36 вариантов»
Задание 15-19 вариант 4 ОГЭ 2022 из 36 вариантов
Задание 15. В треугольнике ABC угол С равен 90°, ВС = 15, АС = 3. Найдите tgB.
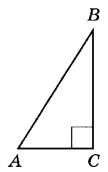
Решение.
Тангенс угла определяется отношением противолежащего катета на прилежащий, то есть:
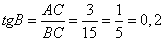
Ответ: 0,2
Задание 16. Угол А трапеции ABCD с основаниями AD и ВС, вписанной в окружность, равен 76°. Найдите угол С этой трапеции. Ответ дайте в градусах.
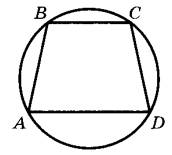
Решение.
Сумма противоположных углов четырехугольника, вписанного в окружность, составляет 180°, то есть:
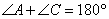
откуда
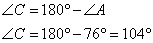
Ответ: 104
Задание 17. Две стороны параллелограмма равны 7 и 12, а один из углов этого параллелограмма равен 30°. Найдите площадь этого параллелограмма.
Решение.
Нарисуем рисунок в соответствии с условиями задачи:
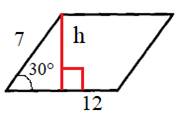
Высота параллелограмма h в 2 раза меньше гипотенузы 7, так как находится напротив угла в 30° (это также можно вычислить через синус 30°):
h = 7:2
Следовательно, площадь параллелограмма, равна:
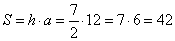
Ответ: 42
Задание 18. На клетчатой бумаге с размером клетки 1x1 изображён прямоугольный треугольник. Найдите длину его большего катета.
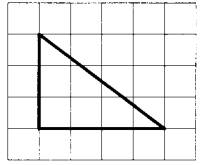
Решение.
Из рисунка видно, что больший катет (нижняя сторона) равен 4 клеткам.
Ответ: 4
Задание 19. Какие из следующих утверждений верны?
1) Один из углов треугольника всегда не превышает 60 градусов.
2) Средняя линия трапеции равна сумме её оснований.
3) Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
Решение.
1) Да, в треугольнике всегда можно найти угол не более (или равный) 60 градусов.
2) Нет, средняя линия равна полусумме оснований.
3) Да, это свойство касательной и радиуса.
Ответ: 13
© 2022, Затеева Валентина Павловна 327 2
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
