Задание № 16. Планиметрия (на доказательство).
1. Прямая, проходящая через вершину B прямоугольника ABCD перпендикулярно диагонали AC, пересекает сторону AD в точке M, равноудалённой от вершин B и D.
а) Докажите, что ∠ABM=∠DBС=30°.
б) Найдите расстояние от центра прямоугольника до прямой CM, если BC=9.
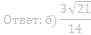
2. К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно.
а) Докажите, что периметр треугольника AMN равен стороне квадрата.
б) Прямая MN пересекает прямую CD в точке P. В каком отношении делит сторону BC прямая, проходящая через точку P и центр окружности, если AM : MB = 1 : 3?
Ответ: б) 1:3
3. Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC=CD.
а) Докажите, что AB:BC=AP:PD.
б) Найдите площадь треугольника COD, где O— центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD— диаметр описанной около четырёхугольника ABCD окружности, AB=6, а BC=6√2.
Ответ: б) 18√3
4. В треугольнике ABC точки A1, B1, C1 — середины сторон BC, AC и AB соответственно, AH— высота, ∠BAC=60°, ∠BCA=45°.
а) Докажите, что точки A1, B1, C1, H— лежат на одной окружности.
б) Найдите A1H, если BC=2√3.
Ответ: б) 1
5. Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.
а) Докажите, что прямые KM и BC параллельны.
б) Пусть L— точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC=16.
Ответ: б) √10
6. Две окружности касаются внутренним образом в точке A, причём меньшая окружность проходит через центр O большей. Диаметр BC большей окружности вторично пересекает меньшую окружность в точке M, отличной от A. Лучи AO и AM вторично пересекают большую окружность в точках P и Q соответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P.
а) Докажите, что прямые PQ и BC параллельны.
б) Известно, что sin ∠AOC=√15/4. Прямые PC и AQ пересекаются в точке K. Найдите отношение QK:KA.
Ответ: б) 1:4
7. Две окружности касаются внутренним образом в точке K, причём меньшая проходит через центр большей. Хорда MN большей окружности касается меньшей в точке C. Хорды KM и KN пересекают меньшую окружность в точках A и B соответственно, а отрезки KC и AB пересекаются в точке L.
а) Докажите, что CN:CM=LB:LA.
б) Найдите MN, если LB:LA=2:3, а радиус малой окружности равен √23.
Ответ: б) 115/6
8. Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N.
а) Докажите, что прямые MN и BO параллельны.
б) Найдите площадь четырёхугольника BOMN, если CN=4 и AM:MC=1:3.
Ответ: б) 7
9. Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK=3 и MK=12.
Ответ: б) 30
10. Точка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MD перпендикулярны.
а) Докажите, что биссектрисы углов при вершинах B и C четырёхугольника ABCD пересекаются на стороне AD.
б) Пусть N— точка пересечения этих биссектрис. Найдите площадь четырёхугольника ABCD, если известно, что BM:MC=1:3, а площадь четырёхугольника, стороны которого лежат на прямых AM, DM, BN и CN, равна 18.
Ответ: б) 96
11. В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно.
а) Докажите, что отрезки AM и MK равны.
б) Найдите MK, если AB=5, AC=8.
Ответ: б) 2,88
12. Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что ∠BAC=∠OBC+∠OCB.
а) Докажите, что точка H лежит на окружности, описанной около треугольника BOC.
б) Найдите угол OHI, если ∠ABC=55°.
Ответ: б) 175
13. Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB=CQ:QB=CW:WD=3:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ=16, QW=12, угол PWQ— острый.
а) Докажите, что треугольник PQW— прямоугольный.
б) Найдите площадь четырёхугольника ABCD.
Ответ: б) 392
14. Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках C1, B1 соответственно.
а) Докажите, что треугольник АВC подобен треугольнику AB1C1.
б) Вычислите длину стороны ВС и радиус данной окружности, если ∠ А= 45°, B1C1= 6 и площадь треугольника AB1C1 в восемь раз меньше площади четырёхугольника BCB1C1.
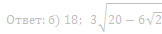
15. Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD.
а) Докажите, что луч AC— биссектриса угла BAD.
б) Найдите CD, если известны диагонали трапеции: AC=15 и BD=8,5.
Ответ: б) 8
16. В прямоугольном треугольнике АВС с прямым углом С точки М и N – середины катетов АС и ВС соответственно, СН – высота.
а) Докажите, что прямые MH и NH перпендикулярны
б) Пусть Р – точка пересечения прямых АС и NH, а Q – точка пересечения прямых ВС и MH. Найдите площадь треугольника PQM, если АН=12 и ВН=3.
Ответ: б) 50
17. В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касается стороны AC в точке M.
а) Докажите, что отрезок BM не больше утроенного радиуса вписанной в треугольник окружности.
б) Найдите sin ∠BMC если известно, что отрезок ВМ в 2,5 раза больше радиуса вписанной в треугольник окружности.
Ответ: б) 0,65
18. В треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно.
а) Докажите, что прямые ЕН и АС параллельны.
б) Найдите отношение ЕН:АС, если угол АВС равен 30.
Ответ: б) 3:4
19. Окружность, вписанная в треугольник KLM, касается сторон KL, LM, MK в точках A, B и C соответственно.
а) Докажите, что KC=(KL+KM-LM)/2 .
б) Найдите отношение LB:BM, если известно, что KC:CM=3:2 и ∠ MKL=60.
Ответ: б) 5:2
20. Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD.
а) Докажите, что четырёхугольник DQOH — параллелограмм.
б) Найдите AD, если ∠BAD = 75° и BC =1.
Ответ: б) 3
21. Квадрат ABCD вписан в окружность. Хорда CE пересекает его диагональ BD в точке K.
а) Докажите, что CK*CE=AB*CD.
б) Найдите отношение CK к KE, если ∠ ECD=15.
Ответ: б) 2:1
22. В прямоугольном треугольнике ABC точки M и N – середины гипотенузы AB и катета BC соответственно. Биссектриса ∠ BAC пересекает прямую MN в точке L
а) Докажите, что треугольники AML и BLC подобны.
б) Найдите отношение площадей этих треугольников, если cos ∠BAC=7/25.
Ответ: б) 25:36
23. Окружность касается стороны AC остроугольного треугольника ABC и делит каждую из сторон AB и BC на три равные части.
а) Докажите, что треугольник ABC равнобедренный.
б) Найдите, в каком отношении высота этого треугольника делит сторону BC.
Ответ: б) 5:4
24. На катетах AC и BC прямоугольного треугольника ABC как диаметрах построены окружности, второй раз пересекающиеся в точке M. Точка Q лежит на меньшей дуге MB окружности с диаметром BC. Прямая CQ второй раз пересекает окружность с диаметром AC в точке P.
а) Докажите, что прямые PM и QM перпендикулярны.
б) Найдите PQ, если AM=1, BM=3, а Q – середина дуги MB.
Ответ: б) 2
25. Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K.
а) Докажите, что отрезок BK втрое больше отрезка CK.
б) Пусть указанная окружность пересекает сторону AB в точке N. Найдите AB, если BK = 24 и BN = 23.
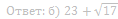
26. В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая – боковых сторон, меньшего основания BC и первой окружности.
а) Прямая, проходящая через центр окружностей, пересекает основание AD в точке P. Докажите, что AP/PD=sin ∠D.
б) Найдите площадь трапеции, если радиусы окружностей равны 3 и 1.
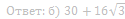
27. В трапецию ABCD с основаниями AD и BC вписана окружность с центром O.
а) Докажите, что sin ∠AOD=sin∠ BOS.
б) Найдите площадь трапеции, если ∠ BAD=90, а основания равны 5 и 7.
Ответ: б) 35
28. Дана трапеция с диагоналями равными 8 и 15. Сумма оснований равна 17.
а) Докажите, что диагонали перпендикулярны.
б) Найдите площадь трапеции.
Ответ: б) 60
29. Дана равнобедренная трапеция, в которой AD = 3BC, CM — высота трапеции.
а) Доказать, что M делит AD в отношении 2:1.
б) Найдите расстояние от точки C до середины BD, если AD = 18, AC=4√13.
Ответ: б) 4
30. В трапеции АBCD ∠BAD прямой. Окружность, построенная на большем основании АD как на диаметре, пересекает меньшее основание BC в точке C и M.
а) Докажите, что ∠BАM равен ∠CАD.
б) Диагонали трапеции АBCD пересекаются в точке O. Найдите площадь треугольника АOB, если АB = 6, а BC = 4BM.
Ответ: б) 20
31. Известно, что АBCD трапеция, АD = 2BC, AD, BC — основания. Точка M такова, что ∠ АBM и ∠MCD прямые.
а) Доказать, что MA = MD.
б) Расстояние от M до AD= BC, а ∠АDC равен 55. Найдите ∠BAD.
Ответ: б) 80
32. Точка E — середина боковой стороны CD трапеции ABCD. На стороне AB взяли точку K, так, что прямые CK и AE параллельны. Отрезки CK и BE пересекаются в точке O.
а) Докажите, что CO = KO.
б) Найти отношение оснований трапеции BC и AD, если площадь треугольника BCK составляет 9/64 от площади трапеции ABCD.
Ответ: б) 3:5
33. Окружность, вписанная в трапецию ABCD, касается ее боковых сторон AB и CD в точках M и N соответственно. Известно, что AM = 8MB и DN = 2CN.
а) Докажите, что AD = 4BC.
б) Найдите длину отрезка MN, если радиус окружности равен √6.
Ответ: б) 4
34. В трапеции ABCD точка E — середина основания AD, точка M — середина боковой стороны AB. Отрезки CE и DM пересекаются в точке O.
а) Докажите, что площади четырёхугольника AMOE и треугольника COD равны.
б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника AMOE, если BC = 3, AD=4.
Ответ: б) 2/9
35. Две окружности с центрами O1 и O2 и радиусами 3 и 4 пересекаются в точках A и B. Через точку A проведена прямая MK пересекающая обе окружности в точках M и K, причем точка A находится между ними.
а) Докажите, что треугольники BMK и O1AO2 подобны.
б) Найдите расстояние от точки B до прямой MK, если O1O2 = 5, MK = 7.
Ответ: б) 84/25
36. Две окружности с центрами O1 и O2 пересекаются в точках A и B, причём точки O1 и O2 лежат по разные стороны от прямой AB. Продолжения диаметра CA первой окружности и хорды CB этой окружности пересекают вторую окружности в точках D и E соответственно.
а) Докажите, что треугольники CBD и O1AO2 подобны.
б) Найдите AD, если ∠ DAE = ∠BAC радиус второй окружности в четыре раза больше радиуса первой и AB=2.
Ответ: б) 8
37. В прямоугольном треугольнике ABC проведена высота CH из вершины прямого угла. В треугольники ACH и BCH вписаны окружности с центрами O1 и O2 соответственно, касающиеся прямой CH в точках M и N соответственно.
а) Докажите, что прямые AO1 и CO2 перпендикулярны.
б) Найдите площадь четырёхугольника MO1NO2, если AC = 20 и BC = 15.
Ответ: б) 3,5
38. Дана трапеция ABCD с боковой стороной AB, которая перпендикулярна основаниям. Из точки А на сторону CD опущен перпендикуляр AH. На стороне AB взята точка E так, что прямые СЕ и СD перпендикулярны.
а) Доказать, что прямые BH и ED параллельны.
б) Найти отношение BH к ED, если ∠ BCD=135.
Ответ: б) 1:2
39. Один из двух отрезков, соединяющих середины противоположных сторон четырехугольника, делит его площадь пополам, а другой в отношении 11:17.
а) Докажите, что данный четырехугольник ‐ трапеция.
б) Найдите отношение оснований этой трапеции.
Ответ: б) 2:5
40. Точки E и K — соответственно середины сторон CD и AD квадрата ABCD. Прямая BE пересекается с прямой CK в точке O.
а) Докажите, что вокруг четырёхугольника ABOK можно описать окружность.
б) Найдите AO, если сторона квадрата равна 1.
Ответ: б) 1
41. На продолжении стороны АС за вершину А треугольника АВС отмечена точка D так, что AD = AB. Прямая, проходящая через точку А, параллельно BD, пересекает сторону ВС в точке M.
а) Докажите, что AM — биссектриса треугольника АВС.
б) Найти площадь SAMBD, если AC = 30, BC = 18 и AB = 24.
Ответ: б) 268,8
42. В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.
а) Докажите, что биссектриса угла С делит отрезок МN пополам
б) Пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.
Ответ: б) 3:1
43. Диагональ AC разбивает трапецию ABCD с основанием AD и BC, из которых AD большее, на два подобных треугольника.
а) Докажите, что ∠ABC = ∠ACD.
б) Найдите отрезок, соединяющий середины оснований трапеции, если известно, что BC = 18, AD = 50 и cos ∠ CAD=3/5.
Ответ: б) 8√13
44. К двум непересекающимся окружностям равных радиусов проведены две параллельные общие касательные. Окружности касаются одной из этих прямых в точках A и B. Через точку C, лежащую на отрезке AB, проведены касательные к этим окружностям, пересекающие вторую прямую в точках D и E, причём отрезки CA и CD касаются одной окружности, а отрезки CB и CE — другой.
а) Докажите, что периметр треугольника CDE вдвое больше расстояния между центрами окружностей.
б) Найдите DE, если радиусы окружностей =5, расстояние между их центрами =18, а AC = 8.
Ответ: б) 12,375
45. Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H.
а) Докажите, что ∠AHB1 = ∠ACB.
б) Найдите BC, если AH = 21 и ∠BAC = 30°.
Ответ: б) 7√3
46. В равнобедренном треугольнике ABC с углом 120° при вершине A проведена биссектриса BD. В треугольник ABC вписан прямоугольник DEFH так, что сторона FH лежит на стороне BC, а вершина E — на стороне AB.
а) Докажите, что FH = 2DH.
б) Найдите площадь прямоугольника DEFH, если AB = 2.
Ответ: б) 6-3√3
47. Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Ответ: б) 3,2
48. Точки A1, B1, C1 — середины сторон соответственно BC, AC и AB остроугольного треугольника ABC.
а) Докажите, что отличная от A1 точка пересечения окружностей, описанных около треугольников A1CB1 и A1BC1, лежит на окружности, описанной около треугольника B1AC1.
б) Известно, что AB = AC = 10 и BC = 12. Найдите радиус окружности, вписанной в треугольник, вершинами которого являются центры окружностей, описанных около треугольников A1CB1, A1BC1 иB1AC1.
Ответ: б) 1,5
49. В треугольник ABC, в котором длина стороны AC меньше длины стороны BC, вписана окружность с центром O. Точка B1 симметрична точке B относительно CO.
а) Докажите, что A, B, O и B1 лежат на одной окружности.
б) Найдите площадь четырёхугольника AOBB1, если AB = 10, AC = 6 и BC = 8.
Ответ: б) 18
50. Диагонали равнобедренной трапеции ABCD с основаниями BC и AD перпендикулярны. Окружность с диаметром AD пересекает боковую сторону CD в точке M, а окружность с диаметром CD пересекает основание AD в точке N. Отрезки AM и CN пересекаются в точке P.
а) Докажите, что в четырёхугольник ABCP можно вписать окружность.
б) Найдите радиус этой окружности, если BC=7, AD=17.
Ответ: б) 4,2
51. Прямая, проходящая через середину M гипотенузы AB прямоугольного треугольника ABC, перпендикулярна CM и пересекает катет AC в точке K. При этом AK:KC=1:2.
а) Докажите, что ∠BAC=30°.
б) Пусть прямые MK и BC пересекаются в точке P, а прямые AP и BK — в точке Q. Найдите KQ, если BC=√21.
Ответ: б) 14
52. В выпуклом четырёхугольнике ABCD точки K, L, M и N — середины сторон AB, BC, CD и AD соответственно. Площади четырёхугольников ABLN и NLCD равны, а площади четырёхугольников KBCM и AKMD относятся как 11:17.
а) Докажите, что прямые BC и AD параллельны.
б) Найдите отношение BC к AD.
Ответ: б) 0,4
53. Точка О — центр окружности, описанной около остроугольного треугольника ABC. На продолжении отрезка AO за точку О отмечена точка K так, что ∠BAC+∠AKC=90°.
а) Докажите, что четырехугольник OBKC вписанный.
б) Найдите радиус окружности, описанной около треугольника KBC, если известно, что радиус окружности, описанной около треугольника АBC равен 12, а cos∠BAC=0,6.
Ответ: б) 10
54. В остроугольном треугольнике ABC провели высоту BH из точки H на стороны AB и BC опустили перпендикуляры HK и HM соответственно.
а) Докажите, что треугольник MBK подобен треугольнику ABC.
б) Найдите отношение площади треугольника MBK к площади четырёхугольника AKMC, если BH = 2, а радиус окружности, описанной около треугольника ABC равен 4.
Ответ: б) 1:15
55. Около равнобедренного треугольника ABC с основанием BC описана окружность. Через точку C провели прямую, параллельную стороне AB. Касательная к окружности, проведённая в точке B, пересекает эту прямую в точке K.
а) Докажите, что треугольник BCK — равнобедренный.
б) Найдите отношение площади треугольника ABC к площади треугольника BCK, если cos∠BAC=3/4.
Ответ: б) 2
56. Прямая, проходящая через вершину В, прямоугольника ABCD, перпендикулярная диагонали АС и пересекает сторону АD в точке M, равноудаленной от вершин В и D.
а) Докажите, что BM и ВD делят угол В на три равных угла.
б) Найдите расстояние от точки пересечения диагоналей прямоугольника ABCD до прямой СМ, если BC=6√21.
Ответ: б) 3
57. Одна окружность вписана в прямоугольную трапецию, а вторая касается большей боковой стороны и продолжений оснований.
а) Докажите, что расстояние между центрами окружностей равно большей боковой стороне трапеции.
б) Найдите расстояние от вершины одного из прямых углов трапеции до центра второй окружности, если точка касания первой окружности с большей боковой стороной трапеции делит её на отрезки, равные 2 и 50.
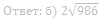
58. В остроугольном треугольнике ABC проведены высоты AK и CM. На них из точек M и K опущены перпендикуляры ME и KH соответственно.
а) Докажите, что прямые EH и AC параллельны.
б) Найдите отношение EH и AC, если ∠ABC=45°
Ответ: б) 1:2
59. Точка М – середина гипотенузы АВ треугольника АВС. Серединный перпендикуляр к гипотенузе пересекает катет ВС в точке N.
а) Докажите, что ∠ CAN = ∠ CMN
б) Найдите отношение радиусов окружностей, описанных около треугольников ANB и CBM, если tg BAC = 4/3.
Ответ: б) 5:4
60. В равнобедренной трапеции ABCD основание AD в два раза больше основания BC.
а) Докажите, что высота CH трапеции разбивает основание AD на отрезки, один из которых втрое больше другого.
б) Пусть O — точка пересечения диагоналей трапеции ABCD. Найдите расстояние от вершины C до середины отрезка OD, если BC=16 и AB=10.
Ответ: б) 4
61. В трапеции ABCD основание AD в два раза больше основания BC. Внутри трапеции взяли точку M так, что углы ABM и DCM прямые.
а) Докажите, что AM=DM.
б) Найдите угол BAD, если угол ADC равен 70°, а расстояние от точки M до прямой AD равно стороне BC.
Ответ: б) 65°
62. Около остроугольного треугольника ABC описана окружность с центром O. На продолжении отрезка AO за точку O отмечена точка K так, что ∠BAC +∠AKC=90°.
а) Докажите, что четырёхугольник OBKC вписанный.
б) Найдите радиус окружности, описанной около четырёхугольника OBKC, если cos ∠BAC=3/5, а BC=48.
Ответ: б)25
63. В равнобедренной трапеции ABCD основание AD в три раза больше основания BC.
а) Докажите, что высота CH трапеции разбивает основание AD на отрезки, один из которых вдвое больше другого.
б) Найдите расстояние от вершины C до середины диагонали BD, если AD=15 и AC=2√61.
Ответ: б) 6
64. В трапеции ABCD боковая сторона AB перпендикулярна основаниям.
Из точки A на сторону CD опустили перпендикуляр AH. На стороне AB отмечена точка E так, что прямые CD и CE перпендикулярны.
а) Докажите, что прямые BH и ED параллельны.
б) Найдите отношение BH к ED, если ∠BCD=120°.
Ответ: б) 3:4
65. В треугольнике ABC угол ABC тупой, H — точка пересечения продолжений высот, угол AHC равен 60°.
а) Докажите, что угол ABC равен 120°.
б) Найдите BH, если AB=7, BC=8.
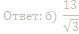
66. В трапеции ABCD с основаниями ВС и AD углы ABD и ACD прямые.
а) Докажите, что АВ = CD.
б) Найдите AD, если AB = 2, BC = 7.
Ответ: б) 8
67. Точка Е — середина стороны BС квадрата АВСD. Серединные перпендикуляры к отрезкам АЕ и ЕС пересекаются в точке O.
а) Докажите, что ∠AOE=90°.
б) Найдите BO:OD.
Ответ: б) 3:1
68. Точка O — центр окружности, описанной около остроугольного треугольника ABC, а BH — высота этого треугольника.
а) Докажите, что углы ABH и CBO равны.
б) Найдите BH, если AB=8, BC=9, BH=BO.
Ответ: б) 6
69. В выпуклом четырёхугольнике ABCD известны стороны и диагональ: AB = 3, BC = CD = 5, AD = 8, AC = 7.
а) Докажите, что вокруг этого четырёхугольника можно описать окружность.
б) Найдите BD.
Ответ: б) 55/7
70. Четырёхугольник ABCD вписан в окружность радиуса R = 8. Известно, что AB=BC=CD=12.
а) Докажите, что прямые BC и AD параллельны.
б) Найдите AD.
Ответ: б) 9
71. Окружность с центром О1 касается оснований ВС и AD и боковой стороны АВ трапеции ABCD. Окружность с центром O2 касается сторон ВС, CD и AD. Известно, что АВ = 10, ВС = 9, CD = 30, AD = 39.
а) Докажите, что прямая О1О2 параллельна основаниям трапеции АВСD.
б) Найдите О1О2.
Ответ: б) 4
72. Окружность с центром в точке O высекает на всех сторонах трапеции ABCD равные хорды.
а) Докажите, что биссектрисы всех углов трапеции пересекаются в одной и той же точке.
б) Найдите высоту трапеции, если окружность пересекает боковую сторону AB в точках K и L так, что AK = 11, KL = 10, LB = 4.
Ответ: б) 24
73. Окружность проходит через вершины A, B и D параллелограмма ABCD, пересекает сторону BC в точках B и E и пересекает сторону CD в точках K и D.
а) Докажите, что AE = AK.
б) Найдите AD, если CE =10, DK = 9 и cos ∠BAD=0,2.
Ответ: б) 40
74. Высоты тупоугольного треугольника АВС с тупым углом АВС пересекаются в точке Н. Угол АНС равен 60 градусов.
а) Докажите, что угол АВС равен 120 градусов
б) Найдите ВН, если АВ=7, ВС=8.
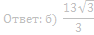
75. В трапецию ABCD c основаниями ВС и AD вписана окружность с центром О, СН – высота трапеции, Е – точка пересечения диагоналей.
а) Докажите, что ∠OHC= ∠ADC / 2.
б) Найдите площадь четырехугольника СЕОН, если известно, что ∠BAD=90°, BC=9, AD=18.
Ответ: б) 21
76. Серединный перпендикуляр к стороне АВ треугольника АВС пересекает сторону АС в точке D. Окружность с центром О, вписанная в треугольник ADB, касается отрезка AD в точке Р, а прямая ОР пересекает сторону АВ в точке К.
а) Докажите, что около четырехугольника ВDОК можно описать окружность.
б) Найдите радиус этой окружности, если АВ = 10, АС = 8, ВС = 6.
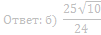
77. Окружность, вписанная в треугольник ABC, касается сторон BC и AC в точках M и N соответственно, E и F — середины сторон AB соответственно. Прямые MN и EF пересекаются в точке D.
а) Докажите, что треугольник DFN равнобедренный.
б) Найдите площадь треугольника BED, если AB = 20 и ∠ABC = 60°.
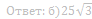
78. Медианы AA1, BB1, CC1 треугольника ABC пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 12.
Ответ: б) 180
79. Четырёхугольник ABCD вписан в окружность. ДиаметрCC1 перпендикулярен стороне AD и пересекает её в точке M, а диаметр DD1 перпендикулярен стороне AB и пересекает её в точке N.
а) Пусть AA1 также диаметр окружности. Докажите, что ∠DNM =∠BA1D1.
б) Найдите углы четырёхугольника ABCD, если угол CDB вдвое меньше угла ADB.
Ответ: б) 72°, 126°, 108°, 54°
80. В прямоугольном треугольнике ABC с прямым углом C известны стороны AC =12, BC = 5. Окружность радиусом 0,5 с центром O на стороне BC проходит через вершину C. Вторая окружность касается катета AC, гипотенузы треугольника, а также внешним образом касается первой окружности.
а) Докажите, что радиус второй окружности меньше, чем 1/5 длины катета AC.
б) Найдите радиус второй окружности.
Ответ: б) 2
81. Окружность с центром O проходит через вершины B и C большей боковой стороны прямоугольной трапеции ABCD и касается боковой стороны AD в точке T.
а) Докажите, что угол BOC вдвое больше угла BTC.
б) Найдите расстояние от точки T до прямой BC, если основания трапеции AB и CD равны 4 и 9 соответственно.
Ответ: б) 6
82. Окружность с центром O, вписанная в треугольник ABC, касается его сторон BC, AB и AC в точках K, L и M соответственно. Прямая KM вторично пересекает в точке P окружность радиуса AM с центром A.
а) Докажите, что прямая AP параллельна прямой BC.
б) Пусть ∠ABC =90°, AM =3, CM =2, Q— точка пересечения прямых KM и AB, а T—такая точка на отрезке PQ, что ∠OAT= 45°. Найдите QT.
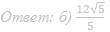
83. На гипотенузе AB и на катетах BC и AC прямоугольного треугольника ABC отмечены точки M, N и K соответственно, причем прямая KN параллельна прямой AB и BM =BN =KN/2. Точка P — середина отрезка KN.
а) Докажите, что четырехугольник BCPM — равнобедренная трапеция.
б) Найдите площадь треугольника ABC, если BM=1 и ∠BCM=15°.
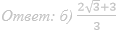
84. В прямоугольном треугольнике ABC точка M лежит на катете AC, а точка N лежит на продолжении катета BC за точку C, причём CM=BC и CN=AC. Отрезки CP и CQ — биссектрисы треугольников ACB и NCM соответственно.
а) Докажите, что CP и СQ перпендикулярны.
б) Найдите PQ, если BC=3, а AC=5.
Ответ: б) 15/4
85. Дана трапеция ABCD с основаниями BC и AD. Точки M и N являются серединами сторон AB и CD соответственно. Окружность, проходящая через точки B и С, пересекает отрезки BM и CN в точках P и Q (отличных от концов отрезков).
а) Докажите, что точки M, N, P и Q лежат на одной окружности.
б) Найдите радиус окружности, описанной около треугольника MPQ, если прямая DP перпендикулярна прямой PC, AB = 25, BC = 3, CD = 28, AD = 20.
Ответ: б) 85/12
86. В остроугольном треугольнике ABC, ∠A=60°. Высоты BN и CM треугольника ABC пересекаются в точке H. Точка O — центр окружности, описанной около ∆ABC.
а) Докажите, что AH=AO.
б) Найдите площадь ∆AHO, если BC=6√3, ∠ABC=45°.
Ответ: б) 9
87. Точка O — центр вписанной в треугольник ABC окружности. Прямая OB вторично пересекает описанную около этого треугольника окружность в точке P.
а) Докажите, что ∠POC=∠PCO.
б) Найдите площадь треугольника APC, если радиус описанной около треугольника ABC окружности равен 4, а ∠ABC=120°.
Ответ: б) 12√3
88. Около остроугольного треугольника ABC с различными сторонами описали окружность с диаметром BN. Высота BH пересекает эту окружность в точке K.
а) Докажите, что AN=CK.
б) Найдите KN, если ∠BAC=35°, ∠ACB=65°, а радиус окружности равен 12.
Ответ: б) 12
89. Около ∆ABC описана окружность. Прямая BO, где O — центр вписанной окружности, вторично пересекает описанную окружность в точке P.
а) Докажите, что OP=AP.
б) Найдите расстояние от точки P до прямой AC, если ∠ABC=120°. а радиус описанной окружности равен 18.
Ответ: б) 27
























