ЗАДАНИЕ 26 ОГЭ.
ГЕОМЕТРИЧЕСКАЯ ЗАДАЧА ПОВЫШЕННОЙ СЛОЖНОСТИ.
ТРЕУГОЛЬНИКИ.
(78) Через середину  медианы
медианы  треугольника
треугольника  и вершину
и вершину 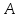 проведена прямая, пересекающая сторону
проведена прямая, пересекающая сторону  в точке
в точке  . Найдите отношение площади треугольника
. Найдите отношение площади треугольника  к площади четырёхугольника
к площади четырёхугольника  .
.
Решение. Обозначим 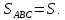
По свойству медианы треугольника (Медиана любого треугольника делит его на два равновеликих (с равными площадями) треугольника), медиана  делит треугольник
делит треугольник  на два равновеликих треугольника:
на два равновеликих треугольника:  .
.
Т.к. точка  - середина
- середина  , то
, то  – медиана треугольника
– медиана треугольника  , значит, делит его на два равновеликих треугольника:
, значит, делит его на два равновеликих треугольника:  .
.
Проведём  . Т.к.
. Т.к. 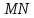 проходит через середину стороны
проходит через середину стороны  и параллельна стороне
и параллельна стороне  , то она является средней линией треугольника
, то она является средней линией треугольника  , значит,
, значит,  .
.
В  отрезок
отрезок  параллелен
параллелен 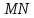 , т.к. является частью отрезка
, т.к. является частью отрезка  , и проходит через середину стороны
, и проходит через середину стороны  , значит, является средней линией
, значит, является средней линией  , поэтому
, поэтому  .
.
Итак, .
По аналогии со свойством медианы, .
Тогда, .
Найдём отношение площади треугольника  к площади четырёхугольника
к площади четырёхугольника  .
.
.
В ответе можно записать любую из предложенных форм записи: либо  , либо
, либо  , либо
, либо  .
.
Ответ:  .
.
(311242) Площадь треугольника  равна
равна  . Биссектриса
. Биссектриса  пересекает медиану
пересекает медиану  в точке
в точке  , при этом
, при этом  . Найдите площадь четырёхугольника
. Найдите площадь четырёхугольника  .
.
Решение. Обозначим 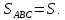
По свойству медианы треугольника (Медиана любого треугольника делит его на два равновеликих (с равными площадями) треугольника), медиана  делит треугольник
делит треугольник  на два равновеликих треугольника:
на два равновеликих треугольника:  .
.
По свойству биссектрисы треугольника (Биссектриса треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам), учитывая, что  , определяем, что
, определяем, что  . Тогда в треугольнике
. Тогда в треугольнике  .
.
Определимся теперь с площадями треугольников.
Треугольники  и
и  имеют общую высоту, выходящую из вершины
имеют общую высоту, выходящую из вершины 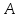 . Обозначим её
. Обозначим её  . Так как
. Так как  , то . Составим формулу площади треугольника
, то . Составим формулу площади треугольника  и выразим через неё площади треугольников
и выразим через неё площади треугольников  и
и  .
.
В треугольнике  высоту, выходящую из вершины
высоту, выходящую из вершины 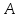 обозначим
обозначим  . Она является общей для трёх треугольников:
. Она является общей для трёх треугольников:  и
и  .
.
Поскольку  , то . Составим формулу площади треугольника
, то . Составим формулу площади треугольника  и выразим через неё площади треугольников
и выразим через неё площади треугольников  и
и  .
.
Найдём теперь площадь четырёхугольника  .
.
Ответ: 
(340325) В треугольнике ABC на его медиане  отмечена точка
отмечена точка  так, что
так, что  . Прямая
. Прямая  пересекает сторону
пересекает сторону  в точке
в точке  . Найдите отношение площади треугольника
. Найдите отношение площади треугольника  к площади четырёхугольника
к площади четырёхугольника  .
.
Решение. Обозначим 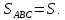
1). По свойству медианы треугольника (Медиана любого треугольника делит его на два равновеликих (с равными площадями) треугольника), медиана  делит треугольник
делит треугольник  на два равновеликих треугольника:
на два равновеликих треугольника:  .
.
2). Треугольники  и
и  имеют общую высоту, выходящую из вершины
имеют общую высоту, выходящую из вершины 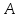 . Обозначим её
. Обозначим её  . По условию, . Составим формулу площади треугольника
. По условию, . Составим формулу площади треугольника  и выразим через неё площади треугольников
и выразим через неё площади треугольников  и
и  .
.
3). Проведём  . Т.к.
. Т.к. 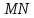 проходит через середину стороны
проходит через середину стороны  и параллельна стороне
и параллельна стороне  , то она является средней линией треугольника
, то она является средней линией треугольника  , значит,
, значит,  .
.
Рассмотрим  и
и  .
.
(по I признаку подобия треугольников). Значит, соответствующие стороны у этих треугольников пропорциональны, т.е.  . По условию,
. По условию,  , значит, . Поскольку
, значит, . Поскольку  , то . Отсюда получаем, что
, то . Отсюда получаем, что  .
.
Треугольники  и
и  имеют общую высоту, выходящую из вершины
имеют общую высоту, выходящую из вершины 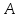 . Обозначим её
. Обозначим её  . Составим формулу площади треугольника
. Составим формулу площади треугольника  и выразим через неё площадь треугольника
и выразим через неё площадь треугольника  .
.
4). Найдём теперь площадь четырёхугольника  .
.
5). Тогда искомое отношение имеет вид:
Ответ можно записать в любом удобном виде.
Ответ:  .
.
(314829) На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо – 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
Решение.
1). Преобразуем жизненную ситуацию в геометрический рисунок.
При опускании, «журавль» описывает два треугольника:  и
и  , причём,
, причём,  .
.
 по I признаку подобия треугольников. Значит, соответствующие стороны у этих треугольников пропорциональны, т.е. .
по I признаку подобия треугольников. Значит, соответствующие стороны у этих треугольников пропорциональны, т.е. .
2). Поскольку высота отмеряется по перпендикуляру к земле, проведём их из точки  и из точки
и из точки 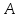 . Получили два прямоугольных треугольника:
. Получили два прямоугольных треугольника:  и
и  .
.
по I признаку подобия треугольников. Значит, соответствующие стороны у этих треугольников пропорциональны, т.е. .
Ответ:  .
.
(315070) Медиана  и биссектриса
и биссектриса  треугольника пересекаются в точке
треугольника пересекаются в точке  , длина стороны
, длина стороны  втрое больше длины стороны
втрое больше длины стороны  . Найдите отношение площади четырёхугольника
. Найдите отношение площади четырёхугольника  к площади треугольника
к площади треугольника  .
.
Решение.
1). Обозначим 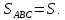
2). По свойству медианы треугольника (Медиана любого треугольника делит его на два равновеликих (с равными площадями) треугольника), медиана  делит треугольник
делит треугольник  на два равновеликих треугольника:
на два равновеликих треугольника:  .
.
3). По свойству биссектрисы треугольника (Биссектриса треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам), учитывая, что  , т.е.
, т.е.  , определяем, что
, определяем, что  . Тогда в треугольнике
. Тогда в треугольнике  .
.
4). Определимся теперь с площадями треугольников.
Треугольники  и
и  имеют общую высоту, выходящую из вершины
имеют общую высоту, выходящую из вершины 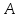 . Обозначим её
. Обозначим её  . Так как
. Так как  , то
, то  . Составим формулу площади треугольника
. Составим формулу площади треугольника  и выразим через неё площадь треугольника
и выразим через неё площадь треугольника  .
.
5). В треугольнике  высоту, выходящую из вершины
высоту, выходящую из вершины 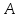 обозначим
обозначим  . Она является общей для трёх треугольников:
. Она является общей для трёх треугольников:  и
и  .
.
Поскольку  , то . Составим формулу площади треугольника
, то . Составим формулу площади треугольника  и выразим через неё площадь треугольника
и выразим через неё площадь треугольника  .
.
6). Найдём теперь площадь четырёхугольника  .
.
7). Определим искомое отношение площадей:
Ответ можно записать в любой предложенной форме.
Ответ: 
(316361) Найдите острые углы прямоугольного треугольника, если его гипотенуза равна  , а площадь равна
, а площадь равна  .
.
Решение. Дан треугольник 
1). Проведём медиану  . В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, пересекает гипотенузу в точке, которая является центром описанной около этого треугольника окружности. Поэтому .
. В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, пересекает гипотенузу в точке, которая является центром описанной около этого треугольника окружности. Поэтому .
2). Проведём высоту  . Из формулы площади треугольника: получаем, что .
. Из формулы площади треугольника: получаем, что .
3). В треугольнике  катет
катет  , гипотенуза
, гипотенуза  , значит, . Мы получаем, что катет равен половине гипотенузы, значит, этот катет лежит напротив угла, равного
, значит, . Мы получаем, что катет равен половине гипотенузы, значит, этот катет лежит напротив угла, равного  , т.е.
, т.е.  .
.
4).  является внешним углом треугольника
является внешним углом треугольника  , поэтому,
, поэтому,  . Но треугольник
. Но треугольник  равнобедренный, у него
равнобедренный, у него  , значит, .
, значит, .
5). В треугольнике .
Ответ:  .
.
(333323) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 96. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 96. Найдите стороны треугольника  .
.
Решение.
1). Биссектриса  и медиана
и медиана  пересекаются в точке
пересекаются в точке  . Т.к.
. Т.к.  , то в треугольнике
, то в треугольнике  является биссектрисой и высотой, поэтому этот треугольник равнобедренный, т.е.
является биссектрисой и высотой, поэтому этот треугольник равнобедренный, т.е.  . Значит,
. Значит,  – медиана, т.е. .
– медиана, т.е. .
2).  – медиана
– медиана  , значит,
, значит,  . Тогда
. Тогда  .
.
3). По свойству биссектрисы (Биссектриса треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам), . Тогда  .
.
4). Проведём отрезок  . Он проходит через середину стороны
. Он проходит через середину стороны  , значит, является средней линией . Мы получили, что
, значит, является средней линией . Мы получили, что  .
.
5). Рассмотрим  и
и  .
.
по I признаку подобия треугольников. Значит, . Тогда .
6). Из  , по теореме Пифагора, . Тогда .
, по теореме Пифагора, . Тогда .
7). В  , по теореме Пифагора, . Тогда .
, по теореме Пифагора, . Тогда .
Ответ: 
(339514) Медиана  и биссектриса
и биссектриса  треугольника
треугольника  пересекаются в точке
пересекаются в точке  , длина стороны
, длина стороны  относится к длине стороны
относится к длине стороны  как
как  . Найдите отношение площади треугольника
. Найдите отношение площади треугольника  к площади четырёхугольника
к площади четырёхугольника  .
.
Решение.
1). Обозначим 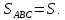
2). По свойству медианы треугольника (Медиана любого треугольника делит его на два равновеликих (с равными площадями) треугольника), медиана  делит треугольник
делит треугольник  на два равновеликих треугольника:
на два равновеликих треугольника:  .
.
3). По свойству биссектрисы треугольника (Биссектриса треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам), учитывая, что  , определяем, что
, определяем, что  . Тогда в треугольнике
. Тогда в треугольнике  .
.
4). Определимся теперь с площадями треугольников.
Треугольники  и
и  имеют общую высоту, выходящую из вершины
имеют общую высоту, выходящую из вершины 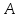 . Обозначим её
. Обозначим её  . Так как
. Так как  , то . Составим формулу площади треугольника
, то . Составим формулу площади треугольника  и выразим через неё площадь треугольника
и выразим через неё площадь треугольника  .
.
5). В треугольнике  высоту, выходящую из вершины
высоту, выходящую из вершины 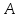 обозначим
обозначим  . Она является общей для трёх треугольников:
. Она является общей для трёх треугольников:  и
и  .
.
Поскольку  , то . Составим формулу площади треугольника
, то . Составим формулу площади треугольника  и выразим через неё площади треугольников
и выразим через неё площади треугольников  и
и  .
.
6). Найдём теперь площадь четырёхугольника  .
.
7). Определим искомое отношение площадей:
Ответ можно записать в любой предложенной форме.
Ответ: 
(311252) Стороны  треугольника
треугольника  равны
равны  соответственно. Точка
соответственно. Точка  расположена вне треугольника
расположена вне треугольника  , причём отрезок
, причём отрезок  пересекает отрезок
пересекает отрезок  в точке, отличной от
в точке, отличной от  . Известно, что треугольник с вершинами
. Известно, что треугольник с вершинами  подобен исходному. Найдите косинус угла
подобен исходному. Найдите косинус угла  , если
, если  .
.
Решение.
1). Треугольник  тупоугольный с тупым углом
тупоугольный с тупым углом  . Поскольку этот треугольник подобен треугольнику
. Поскольку этот треугольник подобен треугольнику  , то в
, то в  также должен быть тупой угол. Для того, чтобы его определить, вспомним свойство треугольника: «Напротив большего угла лежит большая сторона, и, наоборот, напротив большей стороны лежит больший угол». Значит, тупой угол находится напротив стороны
также должен быть тупой угол. Для того, чтобы его определить, вспомним свойство треугольника: «Напротив большего угла лежит большая сторона, и, наоборот, напротив большей стороны лежит больший угол». Значит, тупой угол находится напротив стороны  , равной
, равной  . В соответствии с этими рассуждениями, рисуем чертёж.
. В соответствии с этими рассуждениями, рисуем чертёж.
2). Т.к.  , у них соответствующие углы равны. Из пункта 1) мы определили, что
, у них соответствующие углы равны. Из пункта 1) мы определили, что  . Найдём остальные равные углы. Луч
. Найдём остальные равные углы. Луч  проходит между сторонами угла
проходит между сторонами угла  , значит,
, значит,  , тогда
, тогда  , и тогда
, и тогда  .
.
3). Из подобия треугольников  и
и  следует пропорциональность соответствующих сторон, т.е.
следует пропорциональность соответствующих сторон, т.е.  . Тогда .
. Тогда .
4). По теореме косинусов,
Ответ:  .
.
(340065) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении  , считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна
, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна  .
.
Решение.
1). Биссектрисы треугольника  пересекаются в точке
пересекаются в точке  . Биссектриса
. Биссектриса  делится точкой
делится точкой  в отношении
в отношении  , считая от вершины, т.е.
, считая от вершины, т.е.  .
.
2). По свойству биссектрисы треугольника (Биссектриса треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам), из треугольника  , учитывая, что
, учитывая, что  , определяем, что . Из треугольника
, определяем, что . Из треугольника  .
.
3). Введём обозначение  , тогда
, тогда  (т.к.
(т.к.  и
и  ). Из пропорций, полученных в пункте 2), найдём стороны
). Из пропорций, полученных в пункте 2), найдём стороны  и
и  .
.
4). Найдём периметр треугольника.
Ответ:  .
.
ЗАДАЧИ
ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
(208) Через середину  медианы
медианы  треугольника
треугольника  и вершину
и вершину 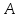 проведена прямая, пересекающая сторону
проведена прямая, пересекающая сторону  в точке
в точке  . Найдите отношение площади четырёхугольника
. Найдите отношение площади четырёхугольника  к площади треугольника
к площади треугольника 
(314831) Через середину  медианы
медианы  треугольника
треугольника  и вершину
и вершину 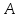 проведена прямая, пересекающая сторону
проведена прямая, пересекающая сторону  в точке
в точке  . Найдите отношение площади треугольника
. Найдите отношение площади треугольника  к площади четырёхугольника
к площади четырёхугольника 
(314999) Через середину  медианы
медианы  треугольника
треугольника  и вершину
и вершину 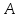 проведена прямая, пересекающая сторону
проведена прямая, пересекающая сторону  в точке
в точке  . Найдите отношение площади треугольника
. Найдите отношение площади треугольника  к площади треугольника
к площади треугольника 
(315043) Через середину  медианы
медианы  треугольника
треугольника  и вершину
и вершину 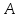 проведена прямая, пересекающая сторону
проведена прямая, пересекающая сторону  в точке
в точке  . Найдите отношение площади треугольника
. Найдите отношение площади треугольника  к площади четырёхугольника
к площади четырёхугольника 
(311261) Площадь треугольника  равна
равна  . Биссектриса
. Биссектриса  пересекает медиану
пересекает медиану  в точке
в точке  , при этом
, при этом  . Найдите площадь четырёхугольника
. Найдите площадь четырёхугольника  .
.
(352430) В треугольнике ABC на его медиане  отмечена точка
отмечена точка  так, что
так, что  . Прямая
. Прямая  пересекает сторону
пересекает сторону  в точке
в точке  . Найдите отношение площади четырёхугольника
. Найдите отношение площади четырёхугольника  к площади треугольника
к площади треугольника  .
.
(341345) В треугольнике ABC на его медиане  отмечена точка
отмечена точка  так, что
так, что  . Прямая
. Прямая  пересекает сторону
пересекает сторону  в точке
в точке  . Найдите отношение площади треугольника
. Найдите отношение площади треугольника  к площади четырёхугольника
к площади четырёхугольника  .
.
(352418) В треугольнике ABC на его медиане  отмечена точка
отмечена точка  так, что
так, что  . Найдите отношение площади треугольника
. Найдите отношение площади треугольника  к площади треугольника
к площади треугольника  .
.
(314937) На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо – 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
(314954) На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо – 3 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
(314955) На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 4 м, а длинное плечо – 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
(314961) На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо – 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
(314965) На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо – 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
(314966) На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо – 7 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
(314967) На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо – 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
(314975) На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо – 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
(314986) На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо – 5 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
(314991) На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо – 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
(314992) На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо – 3 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
(314866) Медиана  и биссектриса
и биссектриса  треугольника пересекаются в точке
треугольника пересекаются в точке  , длина стороны
, длина стороны  втрое больше длины стороны
втрое больше длины стороны  . Найдите отношение площади треугольника
. Найдите отношение площади треугольника  к площади четырёхугольника
к площади четырёхугольника  .
.
(315029) Медиана  и биссектриса
и биссектриса  треугольника пересекаются в точке
треугольника пересекаются в точке  , длина стороны
, длина стороны  втрое больше длины стороны
втрое больше длины стороны  . Найдите отношение площади треугольника
. Найдите отношение площади треугольника  к площади четырёхугольника
к площади четырёхугольника  .
.
(316387) Найдите острые углы прямоугольного треугольника, если его гипотенуза равна  , а площадь равна
, а площадь равна  .
.
(340022) Найдите острые углы прямоугольного треугольника, если его гипотенуза равна  , а площадь равна
, а площадь равна  .
.
(351296) Найдите острые углы прямоугольного треугольника, если его гипотенуза равна  , а площадь равна
, а площадь равна  .
.
(348673) Найдите острые углы прямоугольного треугольника, если его гипотенуза равна  , а площадь равна
, а площадь равна  .
.
(349804) Найдите острые углы прямоугольного треугольника, если его гипотенуза равна  , а площадь равна
, а площадь равна  .
.
(350548) Найдите острые углы прямоугольного треугольника, если его гипотенуза равна  , а площадь равна
, а площадь равна  .
.
(339458) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 92. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 92. Найдите стороны треугольника  .
.
(339507) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 28. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 28. Найдите стороны треугольника  .
.
(339523) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 60. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 60. Найдите стороны треугольника  .
.
(339636) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 152. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 152. Найдите стороны треугольника  .
.
(339710) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 136. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 136. Найдите стороны треугольника  .
.
(339748) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 64. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 64. Найдите стороны треугольника  .
.
(339852) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 104. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 104. Найдите стороны треугольника  .
.
(339853) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 164. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 164. Найдите стороны треугольника  .
.
(339916) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 192. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 192. Найдите стороны треугольника  .
.
(340062) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 160. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 160. Найдите стороны треугольника  .
.
(340091) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 176. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 176. Найдите стороны треугольника  .
.
(333349) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 168. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 168. Найдите стороны треугольника  .
.
(339435) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 208. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 208. Найдите стороны треугольника  .
.
(357152) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 12. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 12. Найдите стороны треугольника  .
.
(357154) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 44. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 44. Найдите стороны треугольника  .
.
(357156) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 16. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 16. Найдите стороны треугольника  .
.
(357158) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 20. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 20. Найдите стороны треугольника  .
.
(357160) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 8. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 8. Найдите стороны треугольника  .
.
(357162) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 24. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 24. Найдите стороны треугольника  .
.
(357163) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 32. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 32. Найдите стороны треугольника  .
.
(357164) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 36. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 36. Найдите стороны треугольника  .
.
(357165) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 40. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 40. Найдите стороны треугольника  .
.
(353380) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 84. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 84. Найдите стороны треугольника  .
.
(351766) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 56. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 56. Найдите стороны треугольника  .
.
(353176) В треугольнике  биссектриса
биссектриса  и медиана
и медиана  перпендикулярны и имеют одинаковую длину, равную 72. Найдите стороны треугольника
перпендикулярны и имеют одинаковую длину, равную 72. Найдите стороны треугольника  .
.
(353377) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении  , считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна
, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна  .
.
(348384) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении  , считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна
, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна  .
.
(348435) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении  , считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна
, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна  .
.
(348459) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении  , считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна
, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна  .
.
(348683) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении  , считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна
, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна  .
.
(348841) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении  , считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна
, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна  .
.
(348925) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении  , считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна
, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна  .
.
(349083) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении  , считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна
, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна  .
.
(349323) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении  , считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна
, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна  .
.
(349443) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении  , считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна
, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна  .
.
(349642) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении  , считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна
, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна  .
.
(350137) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении  , считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна
, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна  .
.
(350512) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении  , считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна
, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна  .
.
(351950) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении  , считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна
, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна  .
.
(352531) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении  , считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна
, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна  .
.
(352655) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении  , считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна
, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна  .
.
(352764) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении  , считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна
, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна  .
.
(352851) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении  , считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна
, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна  .
.
(353016) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении  , считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна
, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна  .
.
ОТВЕТЫ
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| ответ | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| № задания | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| ответ | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| № задания | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| ответ | 
| 
| 
| 
| 
| 
| 
| 
|
| № задания | 29 | 30 | 31 | 32 |
| ответ | 
| 
| | |
| № задания | 33 | 34 | 35 | 36 |
| ответ | 
| 
| 
| |
| № задания | 37 | 38 | 39 | 40 |
| ответ | 
| 
| | |
| № задания | 41 | 42 | 43 | 44 |
| ответ | 
| 
| 
| 
|
| № задания | 45 | 46 | 47 | 48 |
| ответ | 
| 
| 
| 
|
| № задания | 49 | 50 | 51 | 52 |
| ответ | 
| 
| 
| 
|
| № задания | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 |
| ответ | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| № задания | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 |
| ответ | 
| 
| 
| 
| 
| 
| 
| 
| 
|
6







 медианы
медианы  треугольника
треугольника  и вершину
и вершину 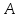 проведена прямая, пересекающая сторону
проведена прямая, пересекающая сторону  в точке
в точке  . Найдите отношение площади треугольника
. Найдите отношение площади треугольника  к площади четырёхугольника
к площади четырёхугольника  .
.
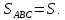
 .
. – медиана треугольника
– медиана треугольника  , значит, делит его на два равновеликих треугольника:
, значит, делит его на два равновеликих треугольника:  .
. . Т.к.
. Т.к. 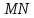 проходит через середину стороны
проходит через середину стороны  и параллельна стороне
и параллельна стороне  , то она является средней линией треугольника
, то она является средней линией треугольника  , значит,
, значит,  .
. отрезок
отрезок 















