Муниципальное автономное общеобразовательное учреждение «Лицей №6»
ЗАДАНИЯ
ДЛЯ ПОДГОТОВКИ К ШКОЛЬНОМУ ЭТАПУ ОЛИМПИАДЫ ПО МАТЕМАТИКЕ
Составитель:
Швецова Ольга Алексеевна,
учитель математики МАОУ «Лицей №6»
ТАМБОВ
2022 г.
Содержание
1. Общие принципы формирования комплектов заданий математических олимпиад 3
2. Общие критерии оценивания 3 3. Порядок проведения школьного этапа олимпиады 4 4. Рекомендуемая тематика заданий школьного этапа олимпиады 4
5. Условия олимпиадных заданий
5.1. Задания для 5 класса 6
5.2. Задания для 6 класса 6
5.3. Задания для 7 класса 7
5.4. Задания для 8 класса 7
5.5. Задания для 9 класса 8
5.6. Задания для 10 класса 8
5.7. Задания для 11 класса 9
6.Решения олимпиадных заданий
6.1. 5 класс 9
6.2. 6 класс 10
6.3. 7 класс 11
6.4. 8 класс 13
6.5. 9 класс 14
6.6. 10 класс 16
6.7. 11 класс 18
7. Рекомендуемая литература 20
1. Общие принципы
формирования комплектов заданий математических олимпиад
Нарастание сложности заданий от первого к последнему. При этом их трудность должна быть такой, чтобы с первыми заданиями могли успешно справиться большинство участников Олимпиады.
Олимпиадные задания школьного этапа составляются на основе программ по математике для общеобразовательных организаций.
Тематическое разнообразие заданий: в комплект должны входить задачи по геометрии, алгебре, комбинаторике, в младших классах – по арифметике, логические задачи; в старших классах желательно включение задач по теории чисел, тригонометрии, стереометрии, математическому анализу. При этом допустимо и даже рекомендуется включение в варианты задач, объединяющих различные разделы школьной математики. В качестве сложных задач возможно включение в вариант задач, использующих материал, изучаемый на факультативных занятиях.
Обязательная новизна задач для участников олимпиады. В случае, когда задания выбираются из печатных изданий или из сети Интернет, методическая комиссия соответствующего этапа должна использовать источники, по возможности не известные участникам. Недопустимо составление комплекта заданий одной олимпиады на основе одного (единственного) источника.
Недопустимость включения в задания задач по разделам математики, не изученным по всем базовым учебникам по алгебре и геометрии в соответствующем классе к моменту проведения олимпиады.
2. Общие критерии оценивания
Задания математических олимпиад являются творческими, допускают несколько различных вариантов решений. Кроме того, необходимо оценивать частичные продвижения в задачах (например, разбор одного из случаев методом, позволяющим решить задачу в целом, доказательство леммы, используемой в одном из доказательств, нахождение примера или доказательства оценки в задачах типа «оценка + пример» и т.п.). Наконец, возможны как существенные, так и не влияющие на логику рассуждений логические и арифметические ошибки в решениях. Окончательные баллы по задаче должны учитывать все вышеперечисленное
В соответствии с регламентом проведения математических олимпиад школьников каждая задача оценивается из 7 баллов.
Соответствие правильности решения и выставляемых баллов приведено в таблице.
| Баллы | Правильность (ошибочность) решения |
| 7 | Полное верное решение. |
| 6-7 | Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение. |
| 5-6 | Решение в целом верное. Однако оно содержит ряд ошибок, либо не рассмотрение отдельных случаев, но может стать правильным после небольших исправлений или дополнений. |
| 4 | Верно рассмотрен один из двух (более сложный) существенных случаев, или в задаче типа «оценка + пример» верно получена оценка. |
| 2-3 | Доказаны вспомогательные утверждения, помогающие в решении задачи. |
| 0-1 | Рассмотрены отдельные важные случаи при отсутствии решения (или при ошибочном решении). |
| 0 | Решение неверное, продвижения отсутствуют. |
| 0 | Решение отсутствует. |
Важно отметить, что любое правильное решение оценивается в 7 баллов. Недопустимо снимать баллы за то, что решение слишком длинное, или за то, что решение школьника отличается от приведенного в методических разработках или от других решений, известных жюри. Важно отметить, что исправления в работе (зачеркивания ранее написанного текста) не являются основанием для снятия баллов.
В то же время любой сколь угодно длинный текст решения, не содержащий полезных продвижений, должен быть оценен в 0 баллов.
Победители и призеры олимпиады определяются жюри в соответствии с итоговой таблицей. Список победителей и призеров утверждается организатором соответствующего этапа олимпиады. Количество победителей и призеров олимпиады не должно превышать 45% от общего числа участников олимпиады. Важно отметить, что победителями олимпиады являются ВСЕ участники, набравшие наибольшие баллы. Поэтому жюри может определить в любом классе более чем одного победителя.
3. Порядок проведения школьного этапа олимпиады
Школьный этап Олимпиады проводится для учащихся 5-11 классов. Вариант должен содержать 4-5 задач разной сложности. Рекомендуется подготовка заданий для школьного этапа Олимпиады муниципальными предметно-методическими комиссиями по математике.
Ниже приводятся темы, которые рекомендуется использовать при составлении вариантов заданий текущего учебного года. Важно отметить, что в силу специфики регионов и различий в степени доступности участникам олимпиады тех или иных источников задач, сложности в составлении (подборе) задач предлагаемой тематики необходимой для данной территории трудности, предметно-методические комиссии могут менять рекомендуемую тематику заданий.
4. Рекомендуемая тематика заданий школьного этапа олимпиады
5 класс
Числовые ребусы.
Задачи на разрезание, переливания, взвешивания.
Логические или текстовые задачи.
Задачи геометрического содержания.
6 класс
Числовые ребусы.
Задачи на составление уравнения.
Свойства геометрических фигур.
Логические или текстовые задачи.
Четность.
7 класс
Числовые ребусы.
Задачи на составление уравнения.
Делимость натуральных чисел.
Задачи на переливания, взвешивания.
Логические задачи.
Задачи геометрического содержания.
8 класс
Преобразование алгебраических выражений.
Построение графиков функций.
Основные элементы треугольника.
Делимость натуральных чисел.
Логические задачи.
9 класс
Делимость.
Квадратный трехчлен и его свойства.
Преобразования алгебраических выражений.
Основные элементы треугольника.
Логические (комбинаторные) задачи.
Задачи геометрического содержания.
10 класс
Квадратный трехчлен и его свойства.
Прогрессии.
Площадь. Подобие фигур.
Неравенства.
Логические (комбинаторные) задачи.
11 класс
Системы уравнений.
Окружность. Свойства вписанных углов.
Тригонометрические уравнения.
Построение графиков функций.
Комбинаторные задачи.
Условия олимпиадных заданий
Лицейская математическая олимпиада для учащихся 5 класса
Малыш может съесть 600 г варенья за 6 минут, а Карлсон – в два раза быстрее. За какое время они съедят это варенье вместе?
В коробке лежат 4 красных и 3 синих карандаша. Их берут в темноте. Сколько надо взять карандашей, чтобы среди них был один синий?
В феврале некоторого года было 2 505 600 секунд. Високосным ли был этот год?
Расстояние между двумя машинами , едущими по шоссе, равно 200 км. Скорости машин: 60 км/ч и 80 км/ч. Какое расстояние будет между ними через час?
Как с помощью прямоугольной плитки размером 7×9 см начертить на листе бумаги отрезок, длина которого 1 см?
Лицейская математическая олимпиада для учащихся 6 класса
Сварили 19 банок варенья и расставили их на трех полках так, чтобы на каждой полке было одинаковое количество варенья. На первую полку поставили 1 большую и 4 средние банки, на вторую – 2 большие и 6 литровых, а на третью – 1 большую, 3 средние и 3 маленькие банки. Сколько литров варенья сварили?
Мальчик и девочка измерили одно и то же расстояние в 143 м шагами, 20 раз их следы совпали. Шаг девочки 55 см. Найти длину шага мальчика.
Гриша с папой пошел в тир. Уговор был такой: Гриша делает пять выстрелов и за каждое попадание в цель получает право сделать еще два выстрела. Всего Гриша сделал 17 выстрелов. Сколько раз Гриша попал в цель?
В бассейне с горизонтальным дном площадью 1 га содержится миллион литров воды. Можно ли в этом бассейне проводить соревнования по плаванию?
Семья состоит из трех человек: отца, матери и сына. В настоящее время сумма их возрастов составляет 74 года, а 10 лет назад эта сумма составляла 47 лет. Сколько лет сейчас отцу, если он старше сына на 28 лет?
Лицейская математическая олимпиада для учащихся 7 класса
Инопланетяне сообщили жителям Земли, что в системе их звезды есть три планеты А, Б, В. Они живут на второй планете. Далее передача ухудшилась из-за помех, но было принято еще два сообщения, которые, как установили ученые, оба неверные:
А – не третья от звезды планета;
Б – вторая планета.
На какой планете (А, Б, или В) живут инопланетяне?
Собака, находясь в пункте А, погналась за лисицей, которая была на расстоянии 30 м от собаки в пункте В. Скачок собаки равен 2 м, скачок лисицы 1 м. Собака делает 2 скачка, в то время как лисица делает 3 скачка. На каком расстоянии от пункта А собака догонит лисицу?
Петя считает пальцы на левой руке от большого пальца до мизинца и обратно от мизинца до большого. Каждый следующий счет приходится на другой палец. На какой палец придется число 2004? (Счет: 1 – большой, 2 – указательный, 3 – средний, 4 – безымянный, 5 – мизинец, 6 – безымянный, 7 – средний и т.д.)
В ящике 25 кг гвоздей. Как с помощью чашечных весов и одной гири в 1 кг за два взвешивания отмерить 19 кг гвоздей?
Влажность свежескошенной травы 60%, сена 15%. Сколько сена получится из одной тонны свежескошенной травы?
Лицейская математическая олимпиада для учащихся 8 класса
Определите, пользуясь линейкой и транспортиром, градусную меру углов четырехугольника, у которого все вершины исключены.
В классе не менее 95,5% и не более 96,5% учеников учатся без двоек. При каком наименьшем количестве учеников это возможно?
В городской олимпиаде по математике участвовали двое близнецов. На вопрос о том, есть ли у них еще братья и какого они возраста, близнецы ответили: «У нас есть брат, его возраст записывается двумя одинаковыми цифрами, а суммарный возраст всех нас троих – двузначное число, у которого вторая цифра вдвое больше первой». Определите возраст братьев.
Доказать, что для любого числа t выполняется неравенство: 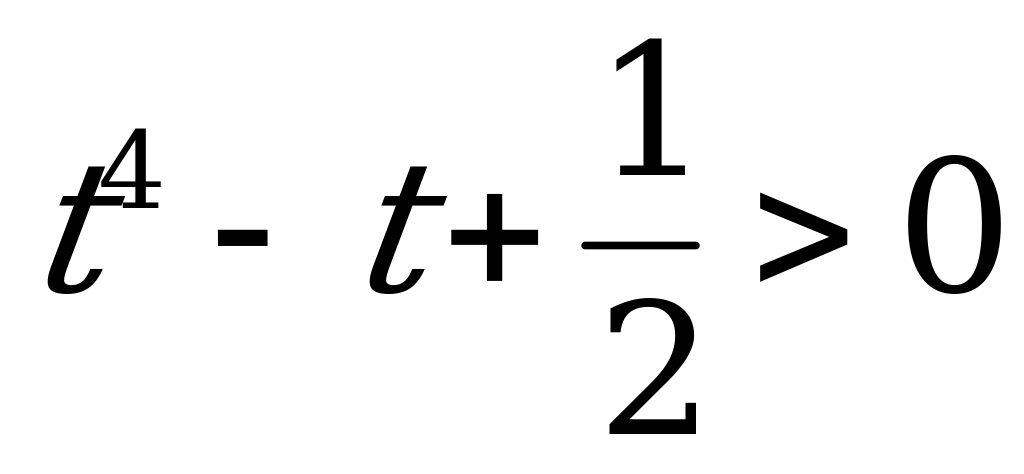 .
.
Двое учащихся – высокий и маленький – вышли одновременно из одного и того же дома в одну школу. У одного из них шаг был на 20% короче, чем у другого, но зато он успевал за то же время делать на 20% больше шагов, чем другой. Кто из них раньше пришел в школу?
Лицейская математическая олимпиада для учащихся 9 класса
На партийный съезд собрались 100 делегатов, каждый из которых либо всегда говорит правду, либо всегда лжет. Первое же заседание по одному покинули 60 делегатов. Выходя из зала, каждый объявил журналистам: «Среди оставшихся там делегатов лжецов больше, чем правдивых». Сколько всего лжецов среди делегатов съезда?
Решить в натуральных числах уравнение ху + уz + хz = 2 (х + у +z).
Каждая грань кубика разбита на четыре квадрата. Всякий отрезок, являющийся общей стороной двух из 24-х полученных квадратов, окрашен в синий или красный цвет. Красных отрезков 26 штук. Докажите, что на поверхности куба найдется замкнутая ломаная линия, состоящая только из красных отрезков.
Все три вершины участка треугольной формы недоступны, вследствие чего стороны и высоты непосредственно измерить нельзя. Как определить площадь этого участка?
Функция f(x) определена на всей числовой оси и является монотонно возрастающей. Решите неравенство f(5) f(x).
Лицейская математическая олимпиада для учащихся 10 класса
Положительные числа a и b таковы, что ab 2021a + 2022b. Доказать, что 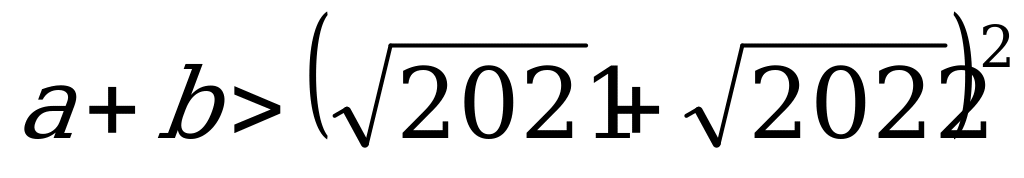 .
.
Выпуклый четырехугольник не поместился на листе бумаги, вне листа оказались все его четыре вершины. Как определить периметр и площадь этого четырехугольника, произведя построения и измерения только на данном листе?
На доске написаны числа 18 и 19. К уже написанным на доске числам разрешается дописать число, равное сумме любых двух из уже написанных. Можно ли, повторяя эту операцию, добиться того, чтобы на доске оказалось написано число 1994?
Масса ста гирек, сваленных в одну кучу, составляет 500г. Известно, что имеются только гирьки в 1 г, в 10 г и 50 г. Сколько в кучке гирек каждой массы?
Функция f(x) определена при всех действительных значениях х и удовлетворяет при всех 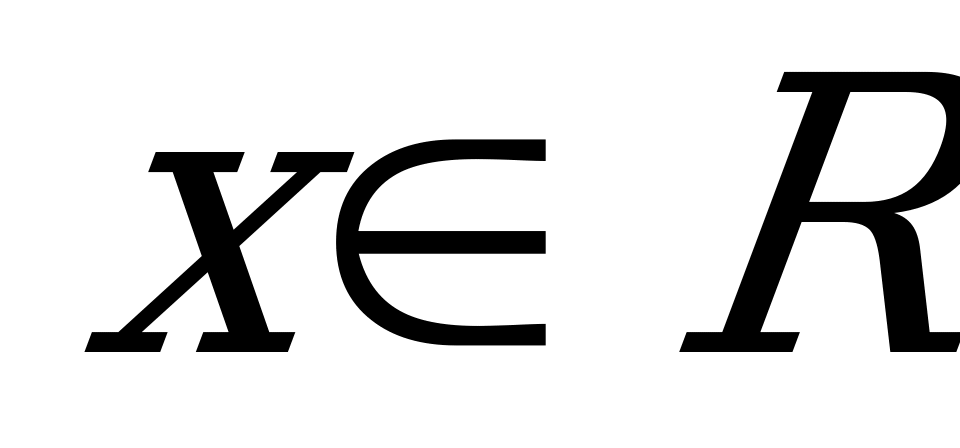 условию 2f (x) + f (1-x) = x2. Найдите f (x).
условию 2f (x) + f (1-x) = x2. Найдите f (x).
Лицейская математическая олимпиада для учащихся 11 класса
Известно, что 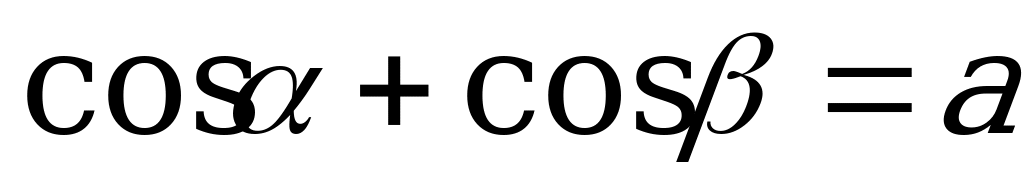 и
и 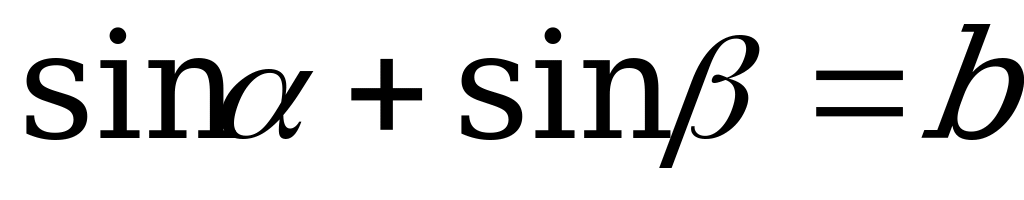 ,
, 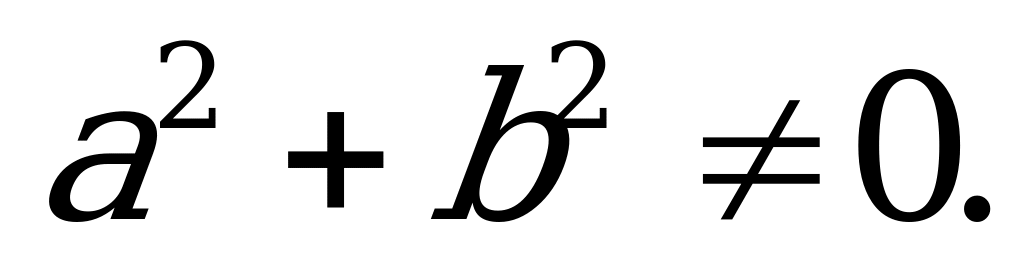 Выразите
Выразите 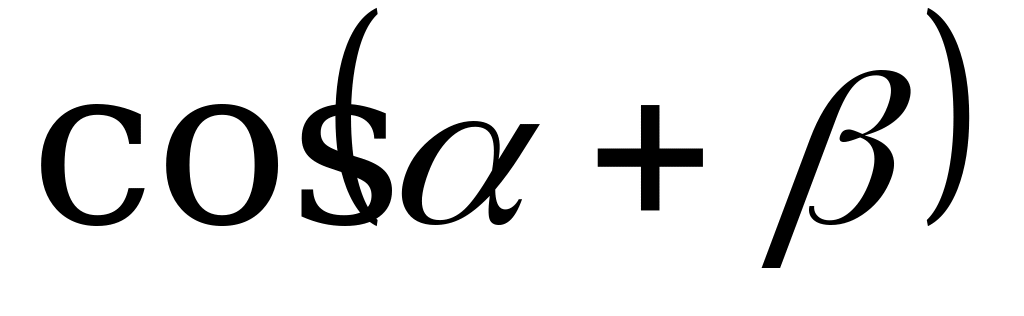 через
через 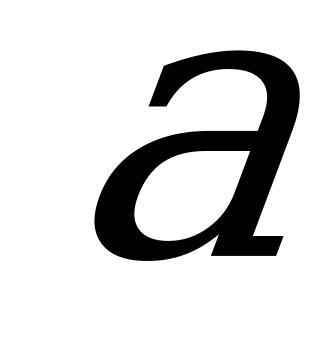 и
и 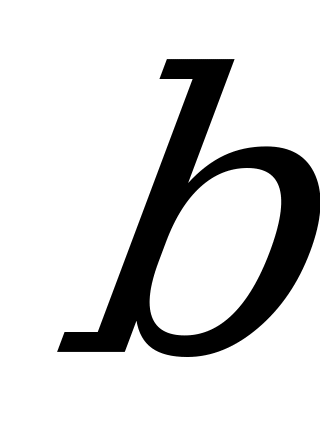 .
.
На доске написаны числа 1, 2, 3, …, 10. Какое наименьшее количество чисел нужно стереть с доски так, чтобы оставшиеся числа можно было разбить на две группы с одинаковыми произведениями чисел в группах?
В коробке лежат красные, желтые и зеленые карандаши трех размеров: короткие, средние и длинные. Известно, что имеются карандаши всех трех цветов и размеров. Верно ли, что обязательно найдутся три карандаша, попарно различающиеся одновременно и по цвету, и по размеру?
Бригады рабочих получили одежду на складе по 2 комплекта на каждого человека. Каждая бригада получила на 20 комплектов больше, чем было бригад. Если бы бригад было на 4 больше и каждой выдавали по 12 комплектов, то одежды на всех не хватило бы. Сколько комплектов было на складе?
Окно состоит из прямоугольника, завершенного равносторонним треугольником. Определить отношение высоты прямоугольной части окна к стороне треугольной части так, чтобы при данном периметре окна оно пропускало бы наибольшее количество света.
6.Решения олимпиадных заданий
6.1. 5 класс
Малыш может съесть 600 г варенья за 6 минут, а Карлсон – в два раза быстрее. За какое время они съедят это варенье вместе?
Решение:
За 1 минуту Малыш съест 600 : 6 = 100 (г). Карлсон может съесть все варенье за 6 : 2 = 3 минуты. Значит, он за 1 мин. Съест 600 : 3 – 200 (г) варенья. Оба они могут съесть за минуту 100 + 200 = 300 (г) варенья. Все варенье совместно съедят за 600 : 300 = 2 (мин.).
В коробке лежат 4 красных и 3 синих карандаша. Их берут в темноте. Сколько надо взять карандашей, чтобы среди них был один синий?
Решение:
5 карандашей. Если взять 4 карандаша, то может оказаться, что все они красные.
В феврале некоторого года было 2 505 600 секунд. Високосным ли был этот год?
Решение:
Да. Так как число 2 505 600 не кратно 28.
Расстояние между двумя машинами, едущими по шоссе, равно 200 км. Скорости машин: 60 км/ч и 80 км/ч. Какое расстояние будет между ними через час?
Решение:
Все зависит от того, в какую сторону ехали автомашины (сделайте рисунок), если: 1) навстречу друг другу , то 60 км; 2) в разные стороны, то 340 км; 3) вторая догоняет первую, то 180 км; 4) вторая «уходит» от первой, то 220 км.
Как с помощью прямоугольной плитки размером 7×9 см начертить на листе бумаги отрезок, длина которого 1 см?
Решение:
Отложим от точки А 4 отрезка по 7 см влево: АА1, А1А2, А2А3 и А3А4, так что АА4 = 28 см. Затем от точки А4отложим три отрезка по 9 см вправо: А4В1, В1В2, В2В3, так что А4В3 = 27 см. Отрезок АВ3 = 1 см – искомый отрезок.
6.2. 6 класс
Сварили 19 банок варенья и расставили их на трех полках так, чтобы на каждой полке было одинаковое количество варенья. На первую полку поставили 1 большую и 4 средние банки, на вторую – 2 большие и 6 литровых, а на третью – 1 большую, 3 средние и 3 маленькие банки. Сколько литров варенья сварили?
Решение:
Пусть х л и у л – вместимость большой и средней банки варенья соответственно. Из условия следует, что х + 4у = 2х + 6 = х + 3у + 3, откуда у = 3, а х = 6. Значение выражения 4х + 7у + 9 при таких х и у равно 54.
Ответ: 54 л варенья.
Мальчик и девочка измерили одно и то же расстояние в 143 м шагами, 20 раз их следы совпали. Шаг девочки 55 см. Найти длину шага мальчика.
Решение:
1) 143 : 20 = 7,15 (м), 715 см – наименьшее расстояние, на котором следы совпали один раз;
2) 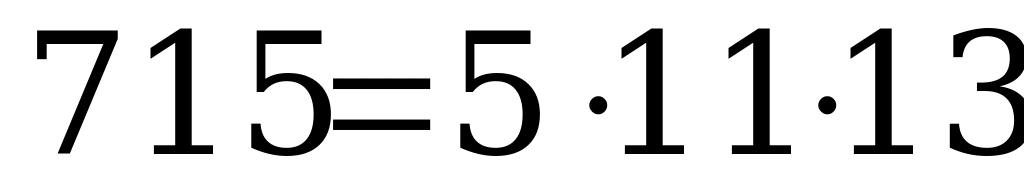 . Шаг девочки 55 см, а шаг мальчика мог быть только или 13 см, или
. Шаг девочки 55 см, а шаг мальчика мог быть только или 13 см, или 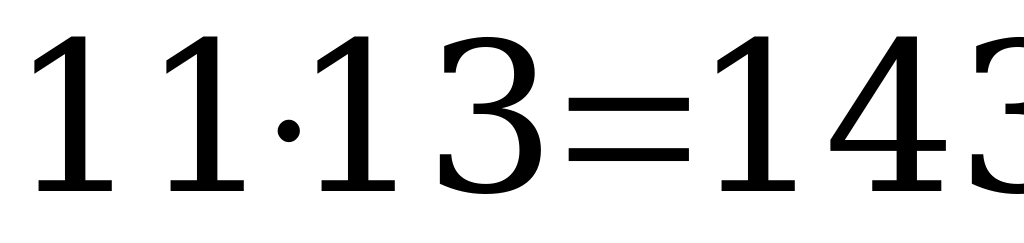 (см), или
(см), или 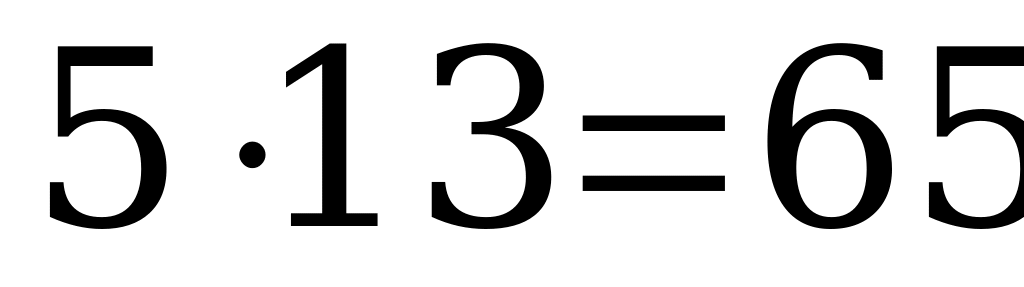 (см). Очевидно, что реальной длиной шага может быть только 65 см.
(см). Очевидно, что реальной длиной шага может быть только 65 см.
Ответ: 65 см.
Гриша с папой пошел в тир. Уговор был такой: Гриша делает пять выстрелов и за каждое попадание в цель получает право сделать еще два выстрела. Всего Гриша сделал 17 выстрелов. Сколько раз Гриша попал в цель?
Решение:
Пусть Гриша из первых пяти выстрелов попал все пять раз. За эти выстрелы он получил еще по два выстрела.
2*5=10.
Ему стало доступно еще десять выстрелов. Итого у него 10+5=15 выстрелов.
Чтобы Гриша мог сделать 17 выстрелов, ему нужно попасть еще раз. Получается, что Гриша 6 раз попал в цель.
│ │ │ │ │
۸ ۸ ۸ ۸ ۸ ۸
Ответ: 6 выстрелов.
В бассейне с горизонтальным дном площадью 1 га содержится миллион литров воды. Можно ли в этом бассейне проводить соревнования по плаванию?
Решение:
1 га = 10 000 кв.м = 1 000 000 кв.дм, т.е. на 1 кв.дм площади поверхности дна приходится 1 л воды. Но 1 л = 1 куб.дм. Следовательно, глубина слоя воды 1 дм. Соревнования по плаванию проводить нельзя.
Семья состоит из трех человек: отца, матери и сына. В настоящее время сумма их возрастов составляет 74 года, а 10 лет назад эта сумма составляла 47 лет. Сколько лет сейчас отцу, если он старше сына на 28 лет?
Решение:
Из того, что 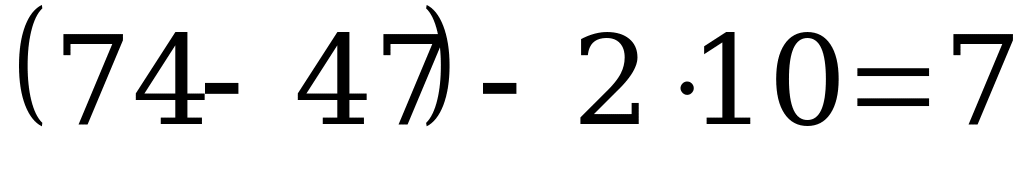 следует, что сейчас сыну 7 лет. Тогда отцу 28+7 = 35 лет.
следует, что сейчас сыну 7 лет. Тогда отцу 28+7 = 35 лет.
Ответ: 35 лет.
6.3. 7 класс
1. Инопланетяне сообщили жителям Земли, что в системе их звезды есть три планеты А, Б, В. Они живут на второй планете. Далее передача ухудшилась из-за помех, но было принято еще два сообщения, которые , как установили ученые, оба неверные:
А – не третья от звезды планета;
Б – вторая планета.
На какой планете (А, Б, или В) живут инопланетяне?
Решение:
Разумные существа живут на планете В.
А – не третья от звезды планета – это сообщение неверно. Значит А – третья планета.
Б – вторая планета – тоже неверно. Значит, Б – первая планета.
Остается принять, что В – вторая планета.
Ответ: планета В.
2. Собака, находясь а пункте А, погналась за лисицей, которая была на расстоянии 30 м от собаки в пункте В. Скачок собаки равен 2 м, скачок лисицы 1 м. Собака делает 2 скачка, в то время как лисица делает 3 скачка. На каком расстоянии от пункта А собака догонит лисицу?
Решение:
За единицу времени собака пробегает 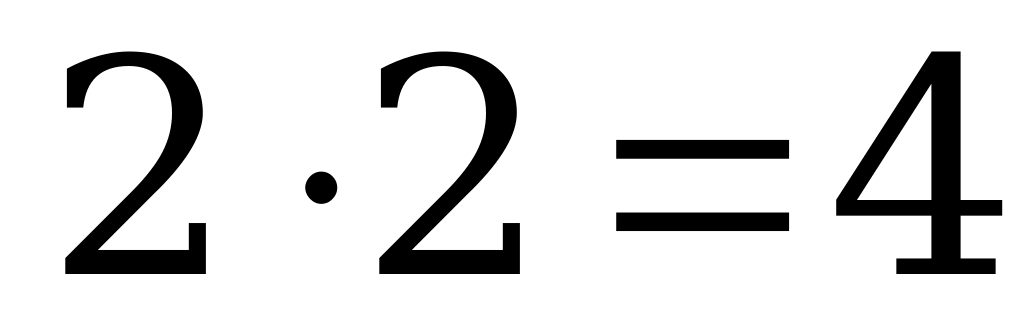 (м), а лисица
(м), а лисица 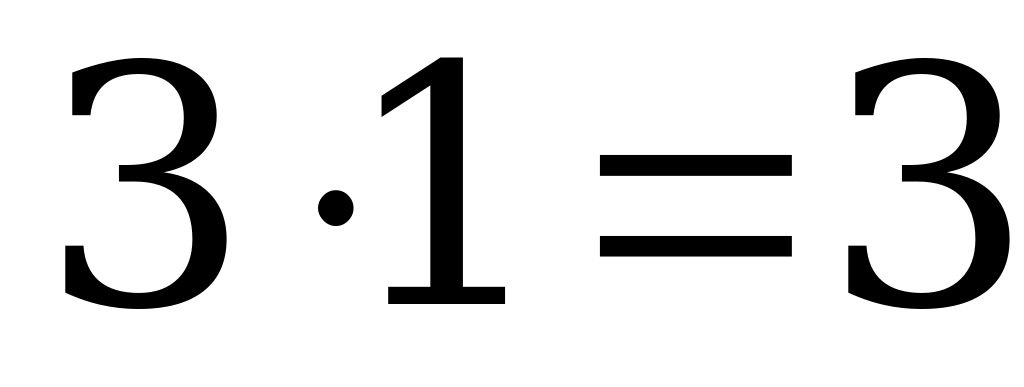 (м), значит за единицу времени собака настигает лисицу на 1 м. Расстояние в 30 м будет покрыто за 30 единиц времени.
(м), значит за единицу времени собака настигает лисицу на 1 м. Расстояние в 30 м будет покрыто за 30 единиц времени.
Ответ: 120м.
3. Петя считает пальцы на левой руке от большого пальца до мизинца и обратно от мизинца до большого. Каждый следующий счет приходится на другой палец. На какой палец придется число 2004? (Счет: 1 – большой, 2 – указательный, 3 – средний, 4 – безымянный, 5 – мизинец, 6 – безымянный, 7 – средний и т.д.)
Решение:
На большой палец приходится счет 1, 9, 17, 25, … ,1993, 2001, так как 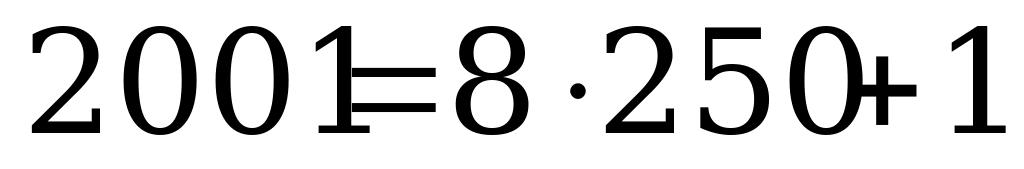 .
.
Ответ: безымянный.
4. В ящике 25 кг гвоздей. Как с помощью чашечных весов и одной гири в 1 кг за два взвешивания отмерить 19 кг гвоздей ?
Решение:
При первом взвешивании в одну из чашек весов кладем гирю и все гвозди раскладываем по чашкам так, чтобы установилось равновесие. Получим 13 и 13 кг гвоздей. Первую кучу откладываем, а остальные гвозди делим пополам, взвешивая без гири: 12=6 + 6. Получили искомое количество гвоздей: 19 = 13 + 6.
5. Влажность свежескошенной травы 60%, сена 15%. Сколько сена получится из одной тонны свежескошенной травы?
Решение:
В 1 тонне свежескошенной травы 60% влаги, т.е. – 600кг, поэтому сухой массы 1000-600=400 кг. Эта масса в сене составит 85%, откуда вес сена составит 400: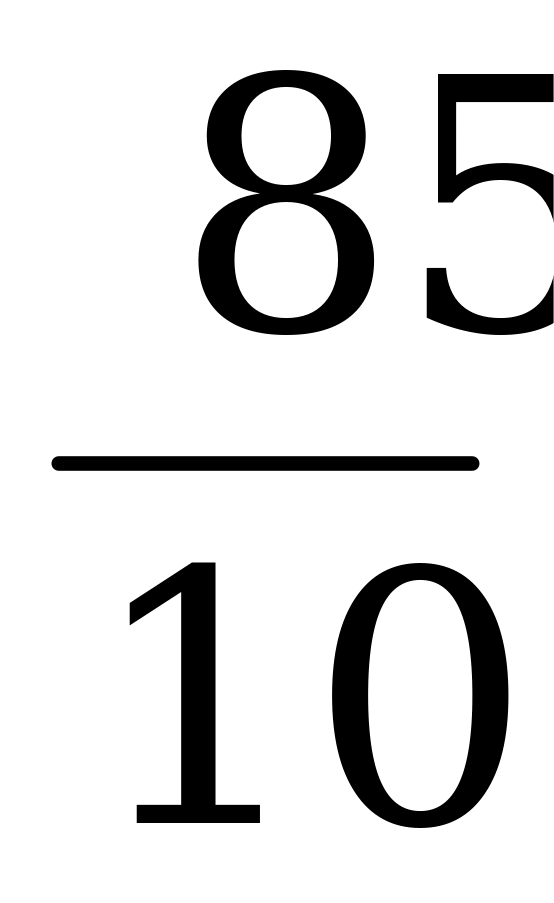 = 470
= 470 кг.
кг.
Ответ: 470  кг.
кг.
6.4. 8 класс
1. Определите, пользуясь линейкой и транспортиром, градусную меру углов четырехугольника, у которого все вершины исключены.
Решение:
Соединим две произвольные точки M и N, принадлежащие смежным сторонам четырехугольника. Получим треугольник, у которого одна сторона MN, а две другие АМ и АN, где А – одна из недоступных вершин четырехугольника. Тогда два угла (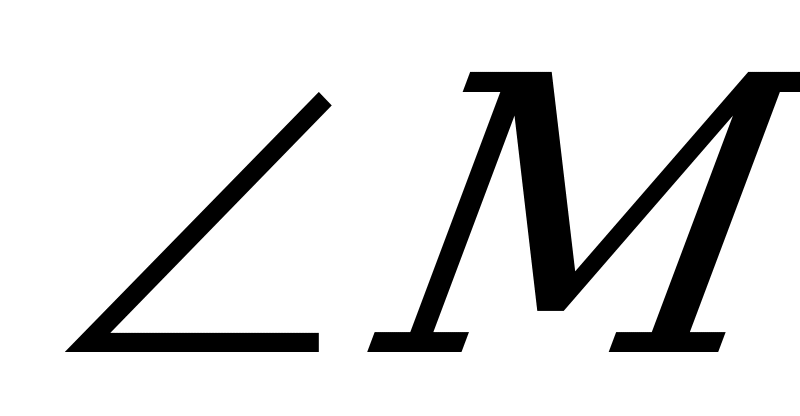 и
и 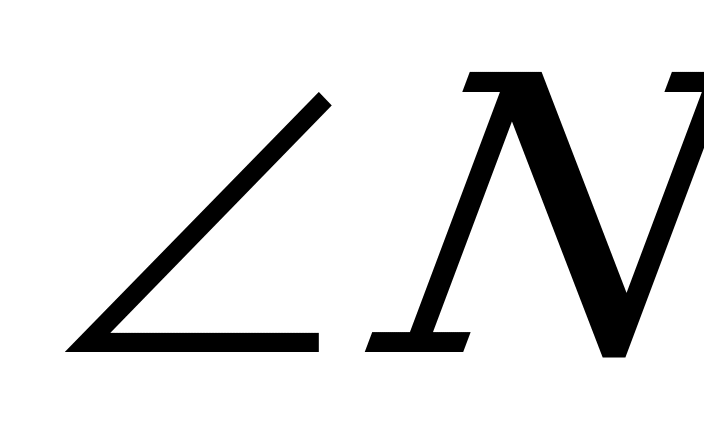 ) треугольника АМN можно измерить , а третий угол (один из возможных углов четырехугольника) – найти вычислением. Таким способом найдем три угла, а четвертый угол определим вычитанием из известной суммы углов четырехугольника суммы трех найденных углов.
) треугольника АМN можно измерить , а третий угол (один из возможных углов четырехугольника) – найти вычислением. Таким способом найдем три угла, а четвертый угол определим вычитанием из известной суммы углов четырехугольника суммы трех найденных углов.
2. В классе не менее 95,5% и не более 96,5% учеников учатся без двоек. При каком наименьшем количестве учеников это возможно?
Решение:
Так как хотя бы один двоечник в классе есть, то меньше всего учеников будет в классе , где двоечник только один. Поскольку двоечников – не более 4,5% от общего числа учеников, то всего в классе не менее 1:0,045 = 22 человек, т.е. не менее 23 человек. Класс из 23 учеников, среди которых ровно один двоечник, удовлетворяет условию задачи. Ответ: 23ученика.
человек, т.е. не менее 23 человек. Класс из 23 учеников, среди которых ровно один двоечник, удовлетворяет условию задачи. Ответ: 23ученика.
3. В городской олимпиаде по математике участвовали двое близнецов. На вопрос о том, есть ли у них еще братья и какого они возраста, близнецы ответили: «У нас есть брат, его возраст записывается двумя одинаковыми цифрами, а суммарный возраст всех нас троих – двузначное число, у которого вторая цифра вдвое больше первой». Определите возраст братьев.
Решение:
Из условия задачи 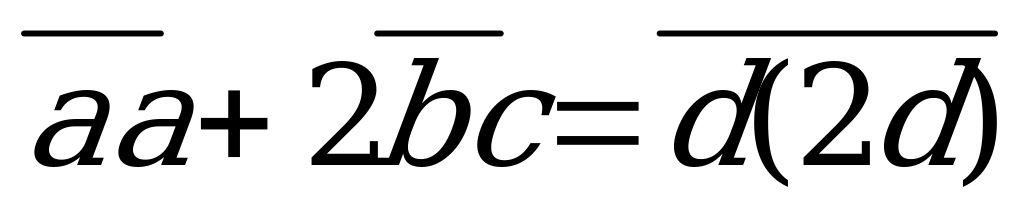 , откуда следует, что a – четная цифра, т.е. a = 2 (теоретически возможно и
, откуда следует, что a – четная цифра, т.е. a = 2 (теоретически возможно и 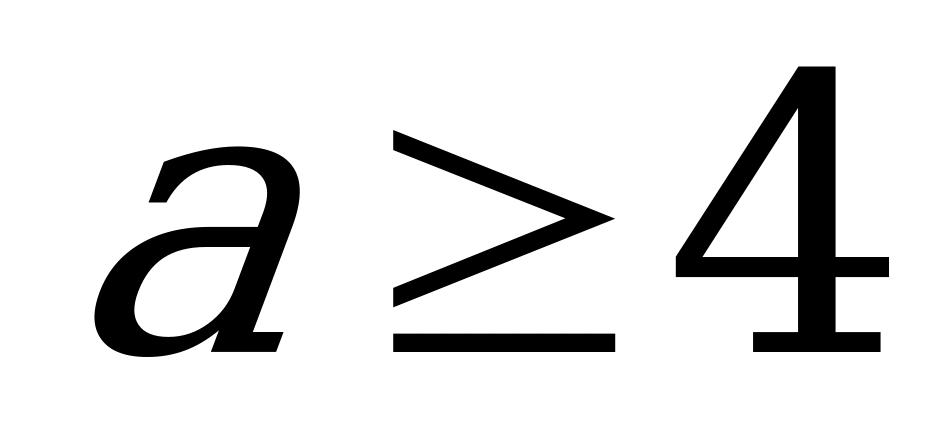 , но тогда
, но тогда 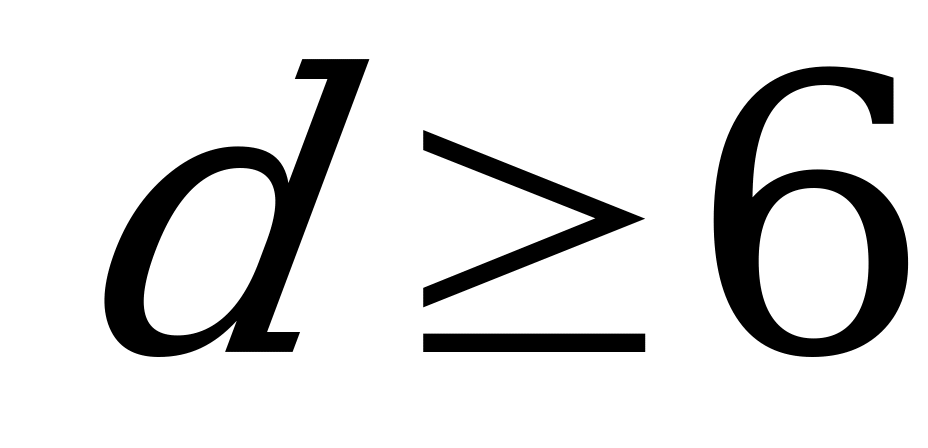 и 2
и 2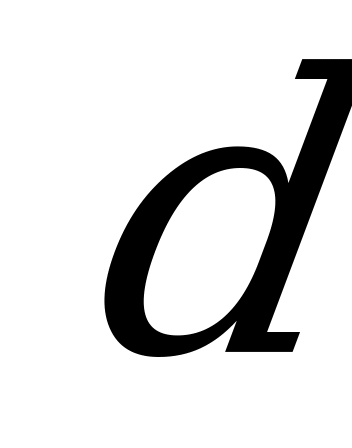 уже не является цифрой). Значит,
уже не является цифрой). Значит, 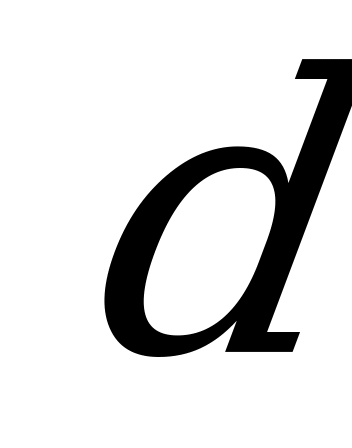 =3 или
=3 или 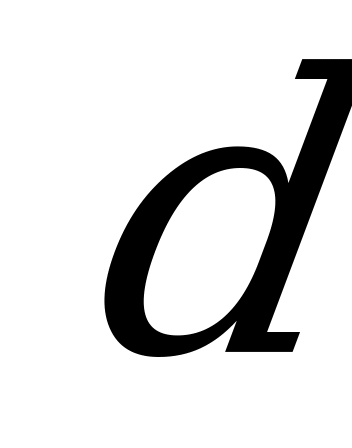 =4. Первое невозможно, т.к. тогда возраст каждого из близнецов -
=4. Первое невозможно, т.к. тогда возраст каждого из близнецов - 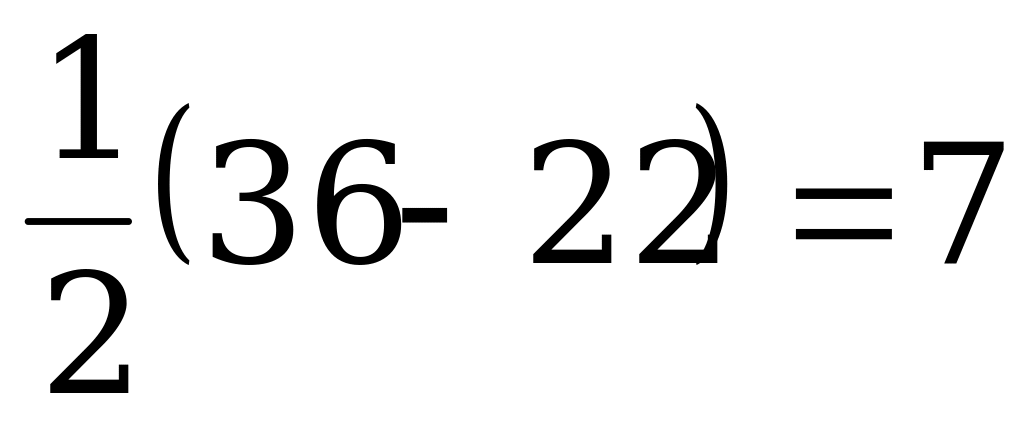 лет, и они не могли участвовать в олимпиаде, во втором случае их возраст
лет, и они не могли участвовать в олимпиаде, во втором случае их возраст 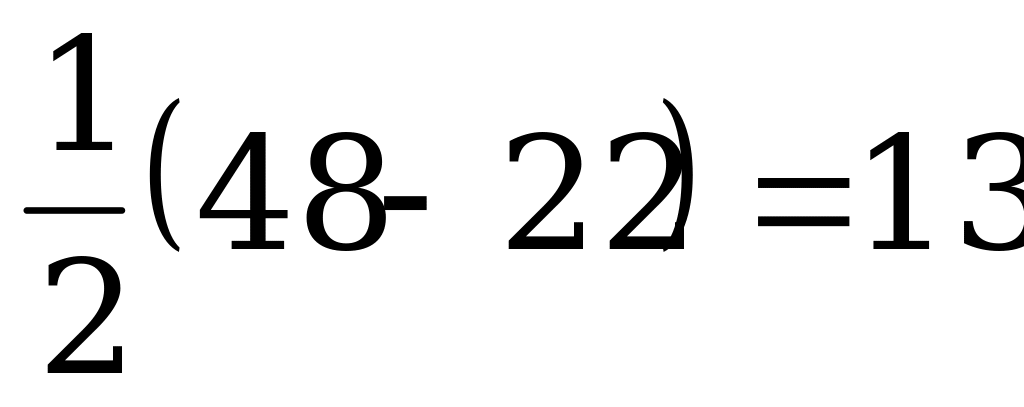 лет.
лет.
Ответ: 13, 13 и 22 года.
4. Доказать, что для любого числа t выполняется неравенство: 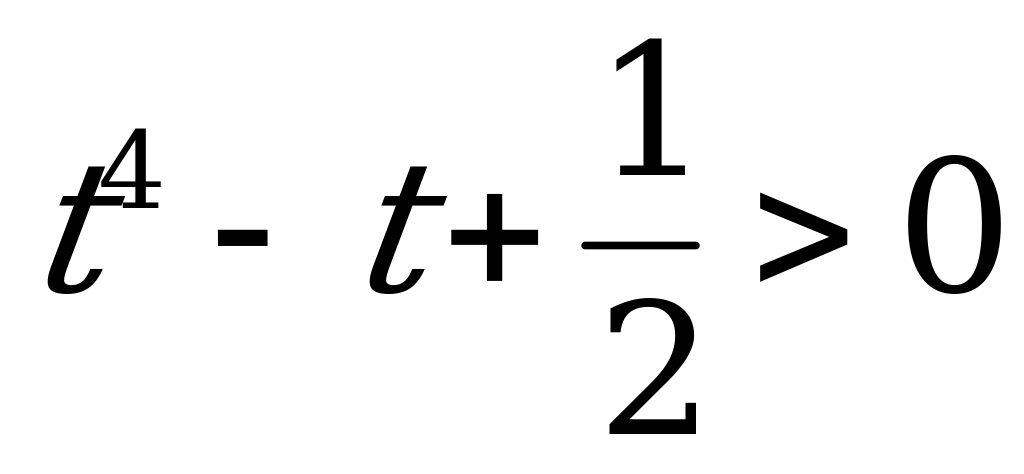 .
.
Решение:
Имеем: 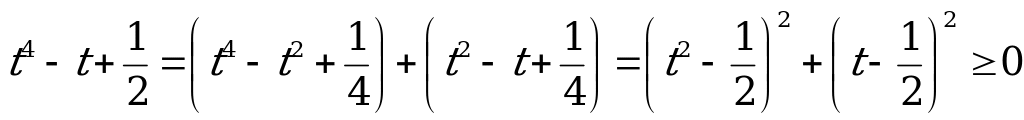 .
.
5. Двое учащихся – высокий и маленький – вышли одновременно из одного и того же дома в одну школу. У одного из них шаг был на 20% короче, чем у другого, но зато он успевал за то же время делать на 20% больше шагов, чем другой. Кто из них раньше пришел в школу?
Решение:
Примем шаг высокого за 1 часть, тогда шаг низкого составит 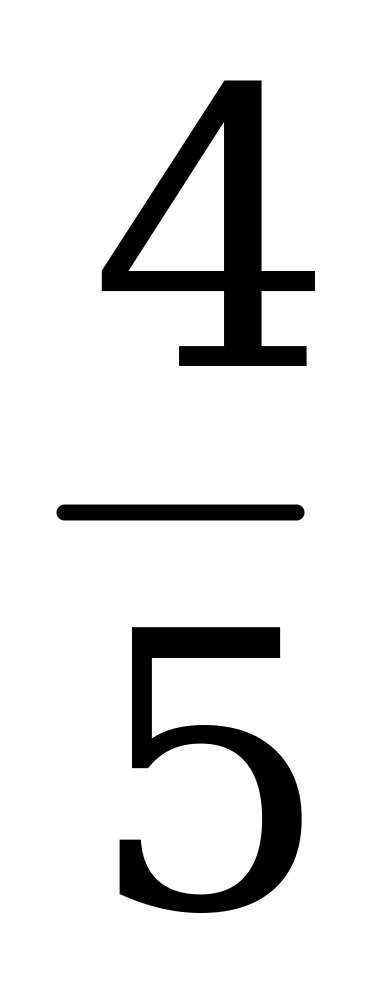 части; на каждые 100 шагов высокого приходится 120 шагов низкого, поэтому за то время, когда высокий пройдет путь в
части; на каждые 100 шагов высокого приходится 120 шагов низкого, поэтому за то время, когда высокий пройдет путь в 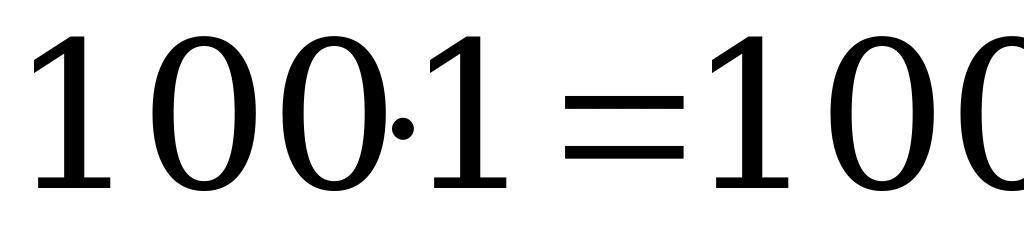 частей, низкий пройдет путь в
частей, низкий пройдет путь в 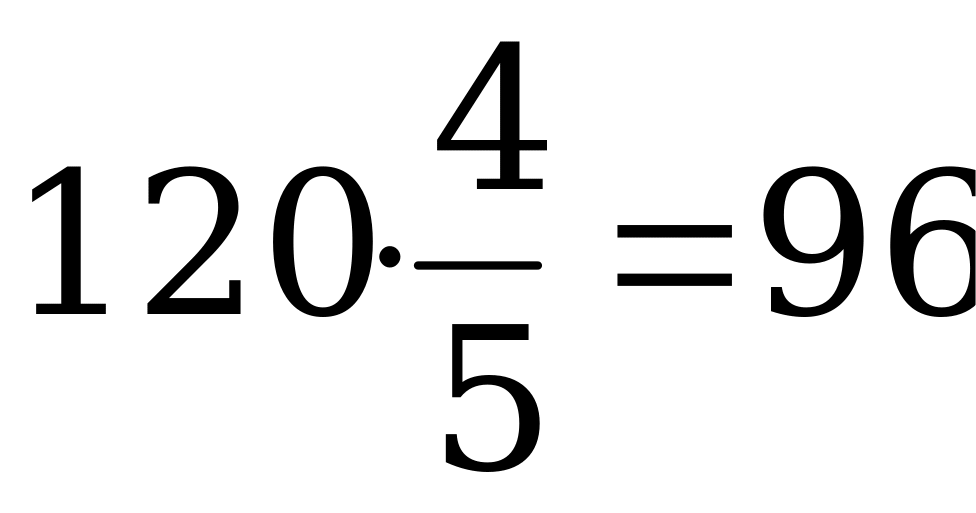 частей, т.е. низкий идет медленнее, значит, придет в школу позднее.
частей, т.е. низкий идет медленнее, значит, придет в школу позднее.
6.5. 9 класс
1. На партийный съезд собрались 100 делегатов, каждый из которых либо всегда говорит правду, либо всегда лжет. Первое же заседание по одному покинули 60 делегатов. Выходя из зала, каждый объявил журналистам: «Среди оставшихся там делегатов лжецов больше, чем правдивых». Сколько всего лжецов среди делегатов съезда?
Решение:
Предположим, что число лжецов превышает 50, а число правдивых, следовательно, не превосходит 49. Тогда среди 60 покинувших заседание обязательно были лжецы, причем лжец, вышедший раньше всех остальных лжецов, сделал свое заявление в тот момент, когда в зале оставалось не менее 50 лжецов. Получается, что заявление, сделанное этим лжецов, было правдивым. Противоречие.
Аналогично доказывается, что и число правдивых делегатов не превышает 50. (Предположив противное, получим, что правдивый, ушедший с заседания раньше всех остальных правдивых, делал свое заявление в момент, когда правдивые в зале составляли большинство).
2. Решить в натуральных числах уравнение ху + уz + хz = 2 (х + у +z).
Решение:
Будем искать решения, удовлетворяющие неравенствам 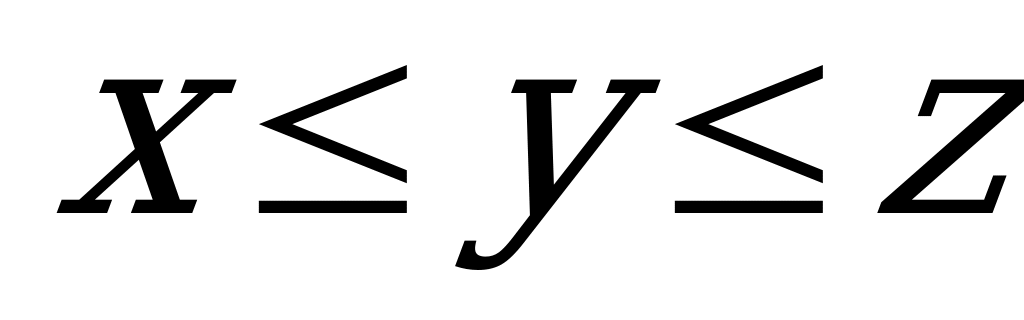 . Если х=1, то уz = 2 +у +z, то есть (у-1)(z-1) = 3, так что у = 2 и z = 4 .Если х = 2, то уz = 4, так что у = z = 2. Убедиться, что при
. Если х=1, то уz = 2 +у +z, то есть (у-1)(z-1) = 3, так что у = 2 и z = 4 .Если х = 2, то уz = 4, так что у = z = 2. Убедиться, что при 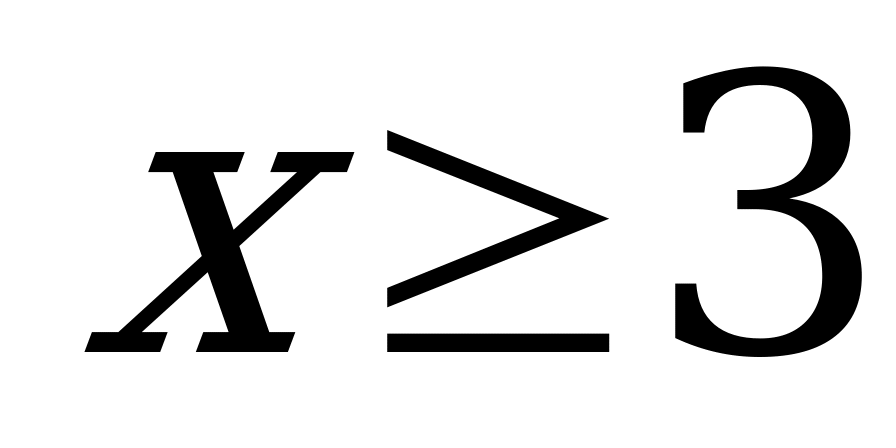
решений нет, можно разными способами. Например, можно переписать уравнение в виде (х-1)(у-1) + (у-1) (z-1) + (z-1)(х-1) = 3.
Или разделить на уz левую и правую части: 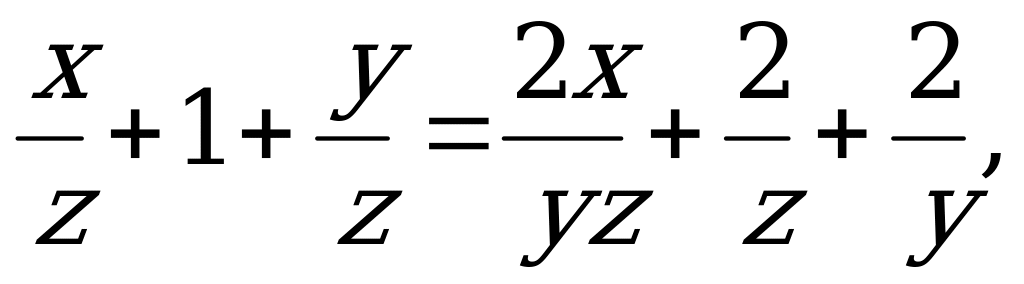 заметив затем, что левая часть больше
заметив затем, что левая часть больше 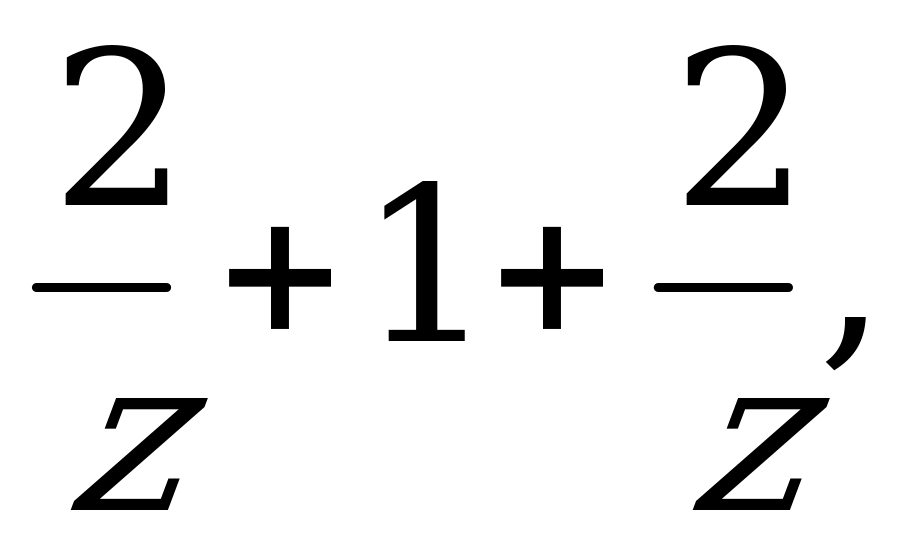 а поэтому
а поэтому 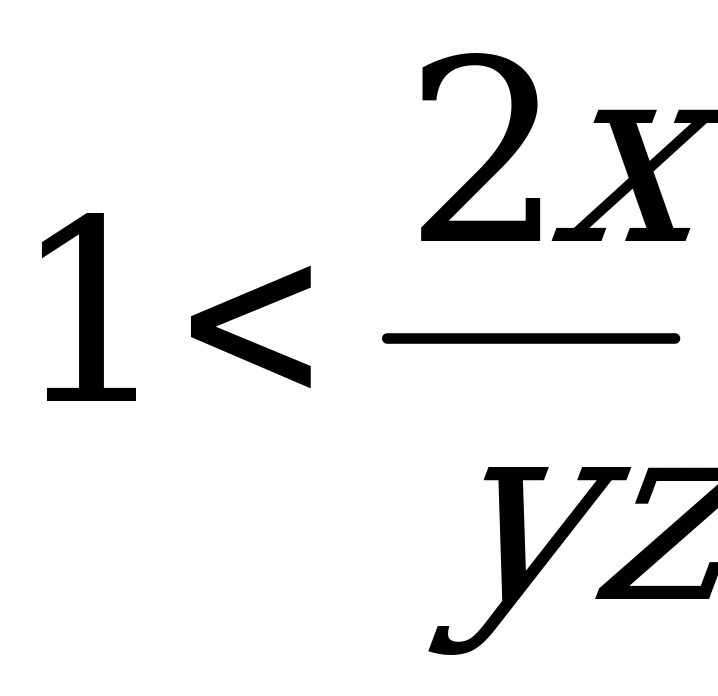 , что невозможно.
, что невозможно.
3. Каждая грань кубика разбита на четыре квадрата. Всякий отрезок, являющийся общей стороной двух из 24-х полученных квадратов, окрашен в синий или красный цвет. Красных отрезков 26 штук. Докажите, что на поверхности куба найдется замкнутая ломаная линия, состоящая только из красных отрезков.
Решение:
Разрежем поверхность кубика по красным линиям. Если при этом поверхность распадется, то это значит, что на поверхности есть хотя бы одна замкнутая линия, состоящая из красных отрезков. Если же поверхность не распалась, то заметим, что синих отрезков 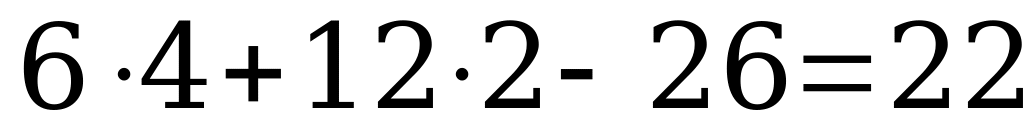 штук, а 22
штук, а 22
Если последнее неравенство кажется не относящимся к делу (точнее, если не ясно, что мы пользовались тем, что в любом связном графе на 24 вершинах должно быть не менее 24-1 ребер), то сожжете рассуждать следующим образом. Будем отрезать квадратики по одному по синим линиям. Чтобы разрезать всю состоящую из 24 квадратиков поверхность на отдельные квадратики, требуется не менее 23 разрезов. Но синих отрезков лишь 22, а 22
4. Все три вершины участка треугольной формы недоступны, вследствие чего стороны и высоты непосредственно измерить нельзя. Как определить площадь этого участка?
Решение:
I способ. Используем теорему (она предварительно доказывается): «Медиана треугольника делит пополам всякий отрезок, соединяющий две точки сторон треугольника и параллельный стороне, к которой проведена медиана».
Пусть имеем треугольник АВС, вершины которого исключены. Проведя в треугольнике АВС два отрезка, параллельные стороне ВС, находим их середины. Полученные две точки определяют прямую, которой принадлежит медиана, проведенная из вершины А. Проведя доступную часть медианы, получим середину стороны ВС – точку N. Аналогично определяется середина стороны АВ – точка М. Значит, МN – средняя линия треугольника АВС, поэтому МN = 0,5 АС.
Из любой точки К средней линии МN опускаем перпендикулярна сторону АС и получаем отрезок KL, равный половине высоты, проведенной к стороне АС. Измерив длины MN и KL, найдем 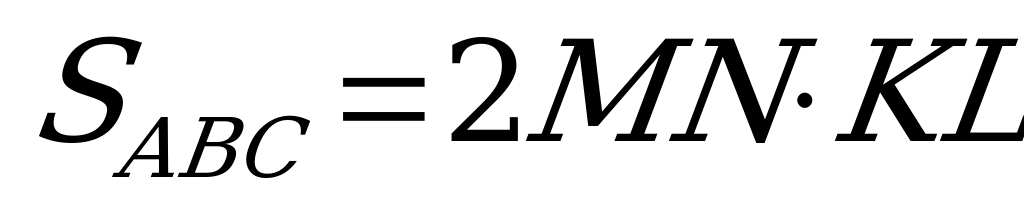 .
.
II способ. Определим длины сторон треугольника АВС (удвоенные соответствующие средние линии). Пусть АВ = с, ВС = а, АС = b. Теперь вычислим площадь треугольника по формуле Архимеда (Герона): 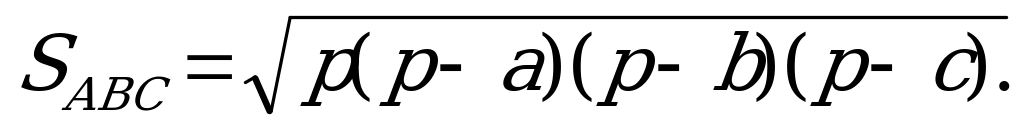
III способ. Построим вспомогательный треугольник А1В1С1, стороны которого соответственно параллельны сторонам данного и равноотстоят от них. Построив биссектрисы углов А1 и В1, найдем точку их пересечения F. Проведем FD 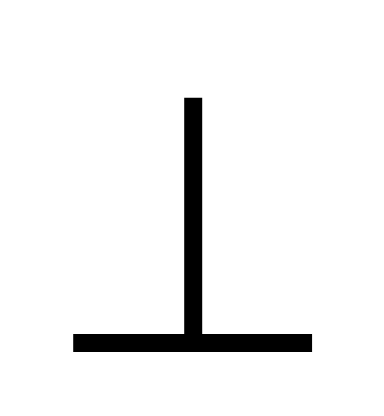 АВ. Треугольники АВС и А1В1С1 подобны. Пусть их коэффициент подобия равен k. Подобны также треугольники AFB и A1FB1. Их коэффициент подобия тоже равен k, поскольку k = АВ : А1В1 = DF : D1F.
АВ. Треугольники АВС и А1В1С1 подобны. Пусть их коэффициент подобия равен k. Подобны также треугольники AFB и A1FB1. Их коэффициент подобия тоже равен k, поскольку k = АВ : А1В1 = DF : D1F.
Отсюда 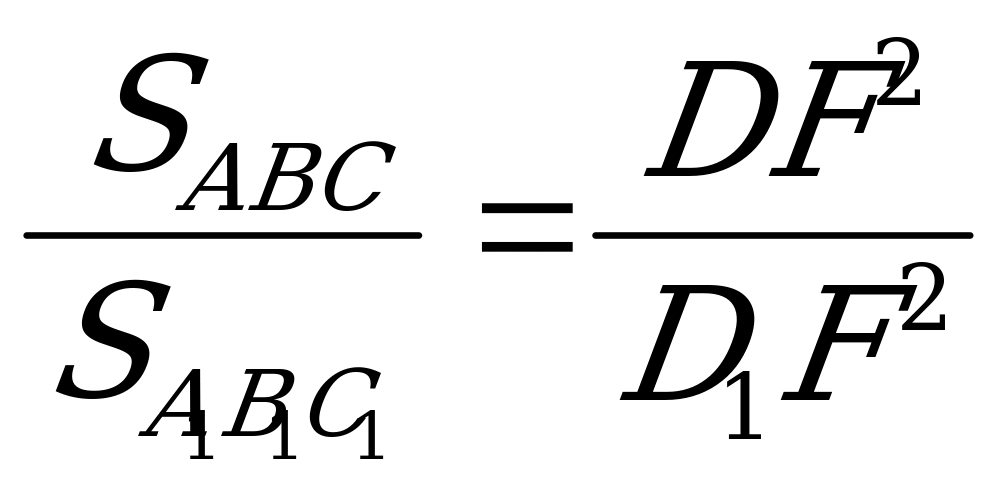 или
или 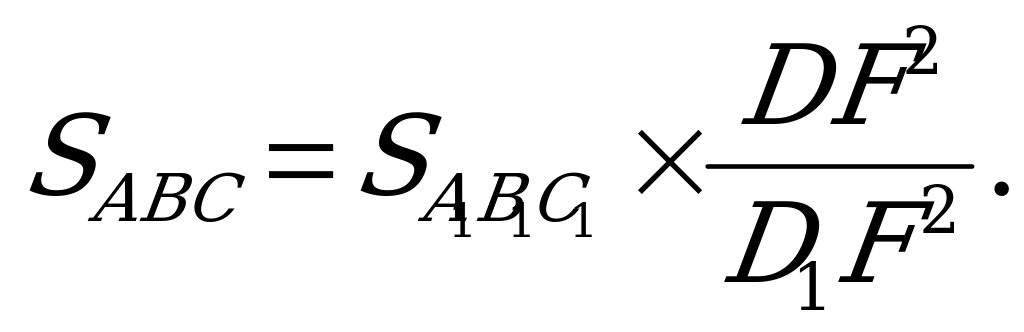 Площадь треугольника А1В1С1, а также длины отрезков DF и D1F доступны для измерения.
Площадь треугольника А1В1С1, а также длины отрезков DF и D1F доступны для измерения.
5. Функция f(x) определена на всей числовой оси и является монотонно возрастающей. Решите неравенство f(5) f(x).
Решение:
Пусть х2х1, где х1 и х2 из области определения функции. Следовательно, f(x2) f(x1). Тогда, если f(5) , то х 5.
6.6. 10 класс
1. Положительные числа a и b таковы, что ab 2021a + 2022b. Доказать, что 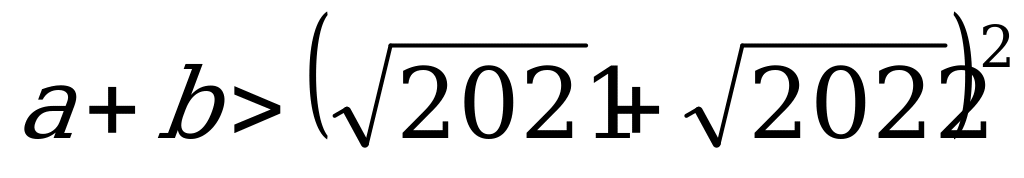 .
.
Решение:
Умножая обе части неравенства ab 2021a + 2022b на 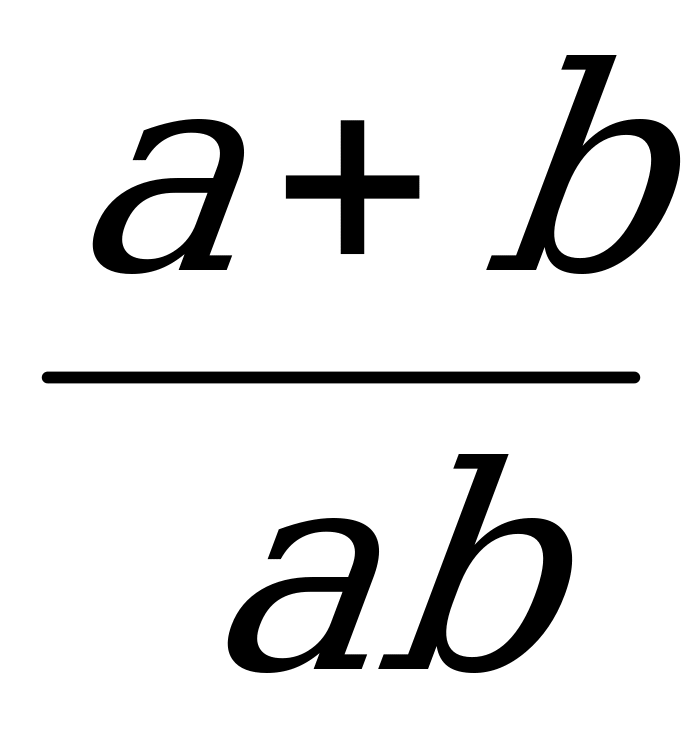 , получим
, получим 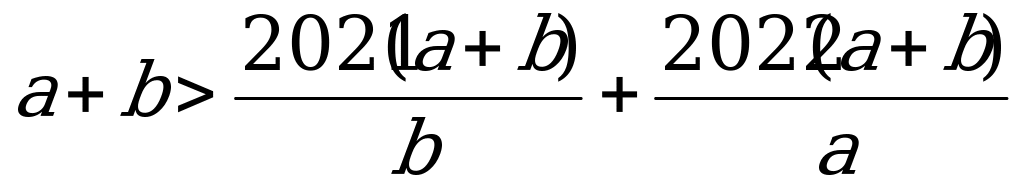 . Утверждение задачи теперь следует из соотношений
. Утверждение задачи теперь следует из соотношений 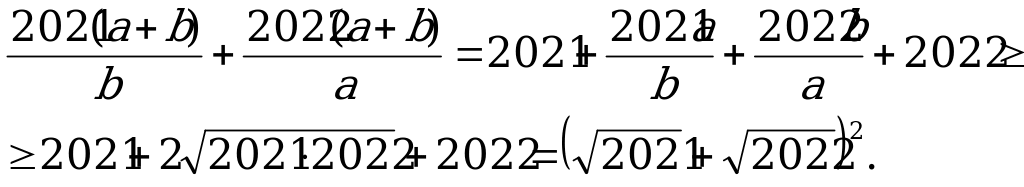
(Использовано неравенство Коши для чисел 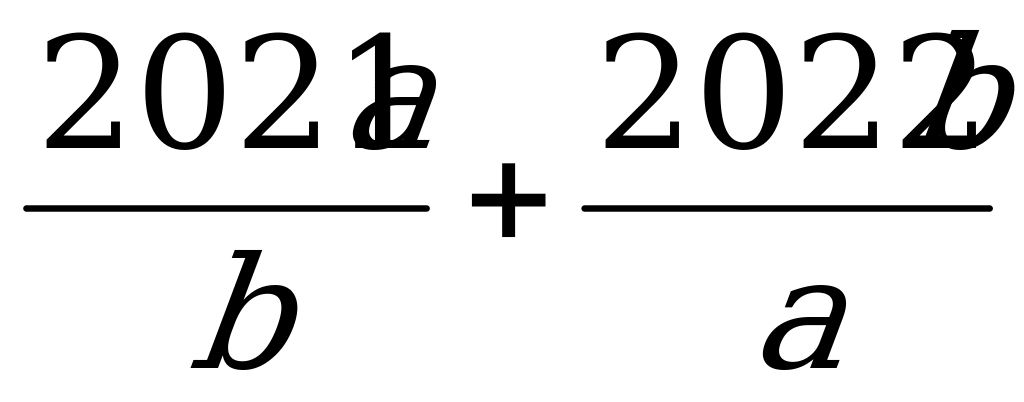 ).
).
2. Выпуклый четырехугольник не поместился на листе бумаги, вне листа оказались все его четыре вершины. Как определить периметр и площадь этого четырехугольника, произведя построения и измерения только на данном листе?
Решение:
I способ. Пусть M, N, K и L – произвольные точки на сторонах данного четырехугольника АВСД. В треугольниках МВN и NСК находим середины сторон ВN и СN – точки F и E. Тогда FE = 0,5ВС, откуда ВС=2FE. Определив таким же образом и другие стороны, находим периметр.
II способ. Проведя PQ||АД и PQ||АВ, получим параллелограмм АPQR, поэтому АP+АR=PQ+QR. Построив такие параллелограммы у каждой вершины четырехугольника, легко определить искомый периметр.
При определении площади воспользуемся таким фактом: середины сторон произвольного четырехугольника являются вершинами параллелограмма, площадь которого равна половине площади данного четырехугольника.
Чтобы найти, например, середину стороны ВС, достаточно от точки F отложить отрезок, равный NE. Так же определяются остальные три вершины вспомогательного параллелограмма. В полученном параллелограмме все элементы доступны для непосредственного измерения, поэтому площадь определяется легко.
3.На доске написаны числа 18 и 19. К уже написанным на доске числам разрешается дописать число, равное сумме любых двух из уже написанных. Можно ли, повторяя эту операцию, добиться того, чтобы на доске оказалось написано число 1994?
Решение:
Число 1994 можно представить в виде 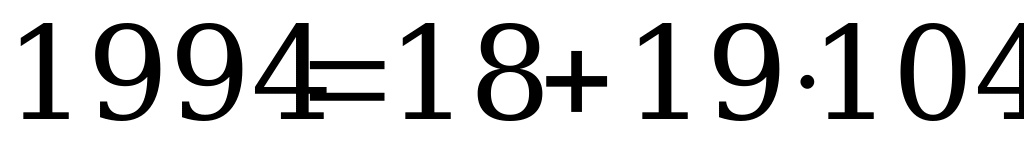 . Поэтому операции, при которых к уже полученной сумме добавляется число 19, приведут к появлению на доске числа 1994: 18+19 = 37, 37 + 19 = 56, …, 1975 +19 = 1994.
. Поэтому операции, при которых к уже полученной сумме добавляется число 19, приведут к появлению на доске числа 1994: 18+19 = 37, 37 + 19 = 56, …, 1975 +19 = 1994.
Ответ: можно.
4. Масса ста гирек, сваленных в одну кучу, составляет 500г. Известно, что имеются только гирьки в 1 г, в 10 г и 50 г. Сколько в кучке гирек каждой массы?
Решение:
Обозначим через х, у, z число гирек массой 1 г, 20 г и 50 г соответственно. По условию задачи
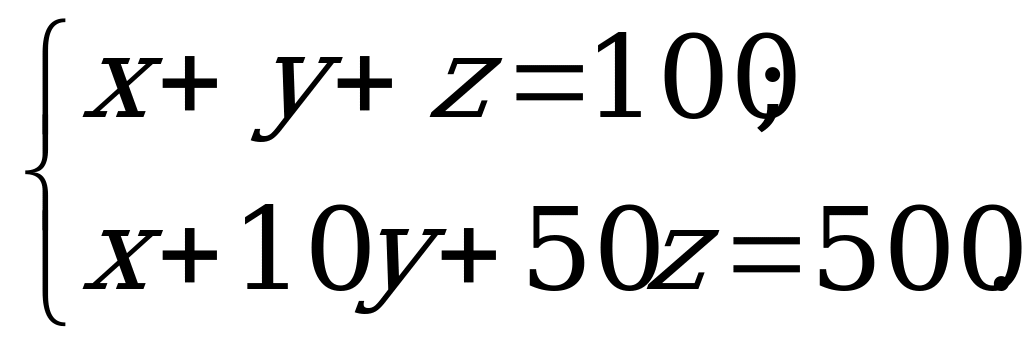
Требуется найти неотрицательные целые числа х, у, z, удовлетворяющие этой системе. Вычитая из второго уравнения системы первое, получаем уравнение
9у + 49z = 400. (1)
Отсюда следует, что 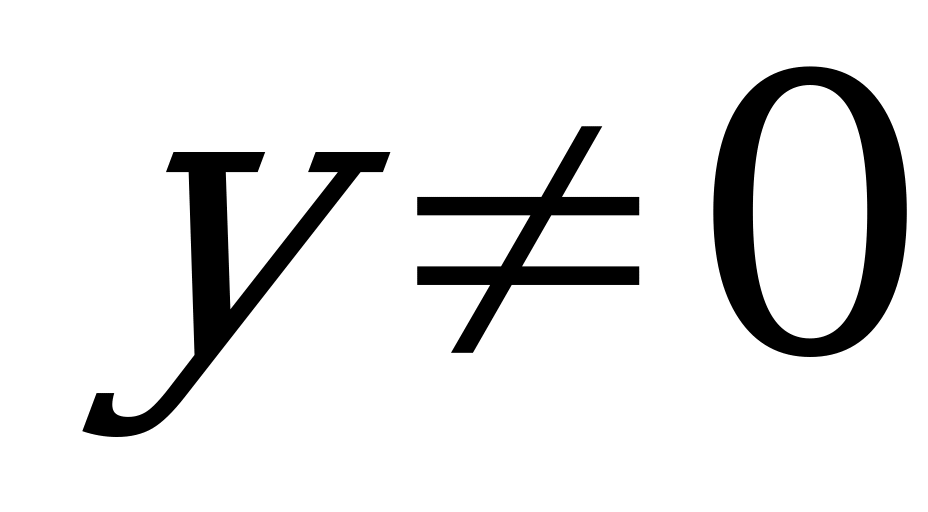 и
и 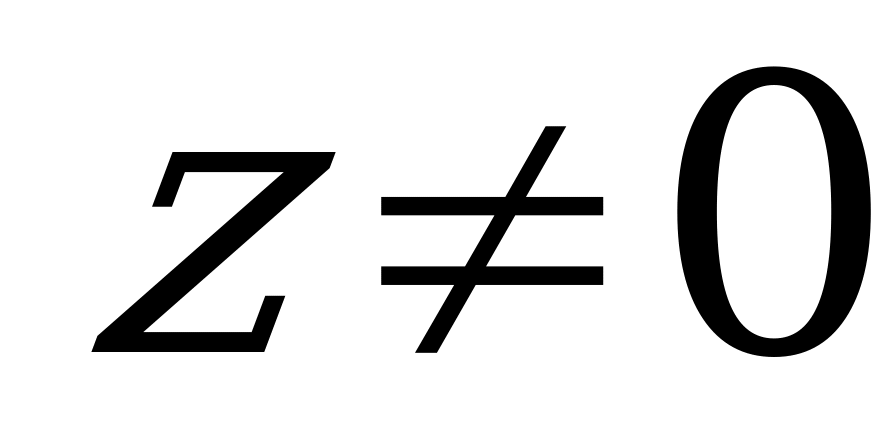 , т.е.
, т.е. 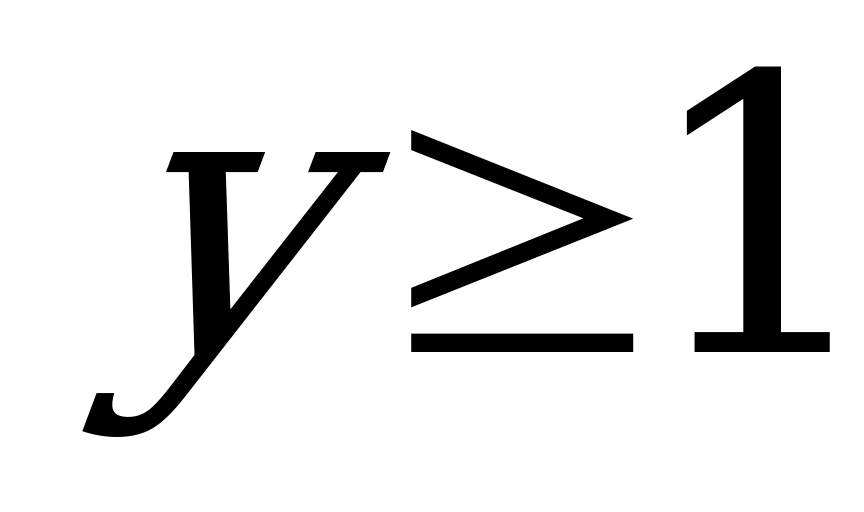 ,
,  (при у=0 уравнение (1) примет вид 49z = 100, а это уравнение не имеет решений в целых числах; при z = 0 получаем уравнение 9у = 100, которое также не имеет целочисленных решений).
(при у=0 уравнение (1) примет вид 49z = 100, а это уравнение не имеет решений в целых числах; при z = 0 получаем уравнение 9у = 100, которое также не имеет целочисленных решений).
Из неравенства 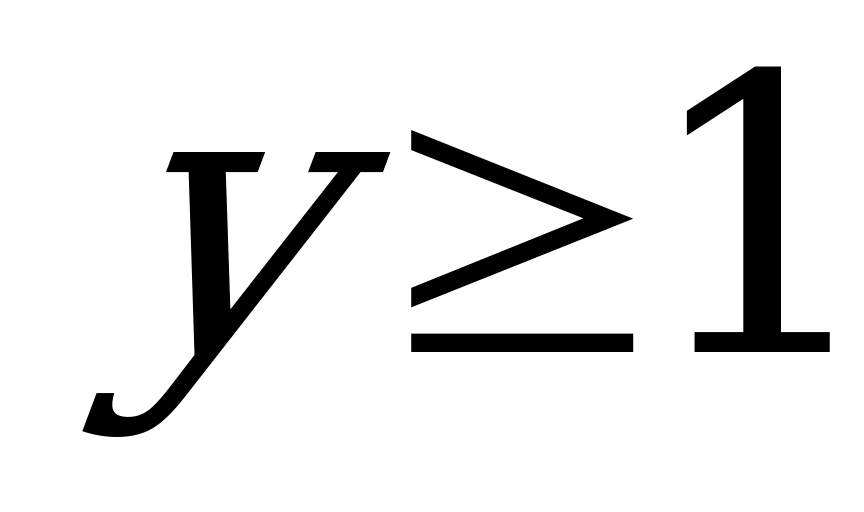 и уравнения (1) получаем 49z = 400 – 9у
и уравнения (1) получаем 49z = 400 – 9у 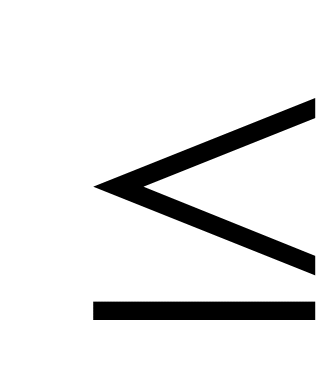 391, zz удовлетворяет неравенствам
391, zz удовлетворяет неравенствам 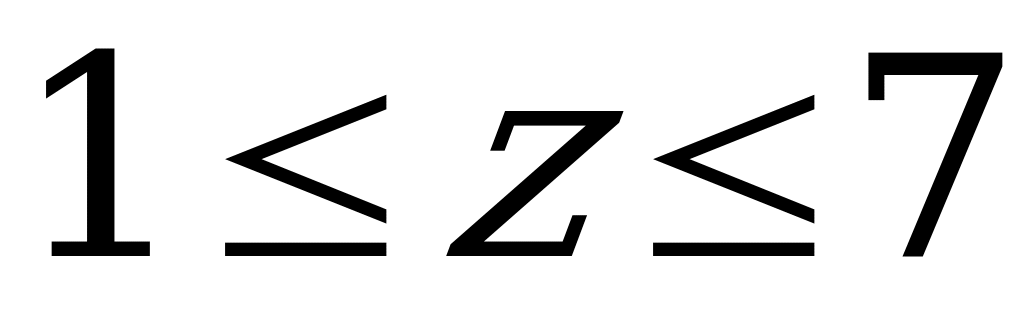 .
.
Из уравнения (1) следует, что число 400 – 49z должно делиться на 9.
А так как 400 – 49z = 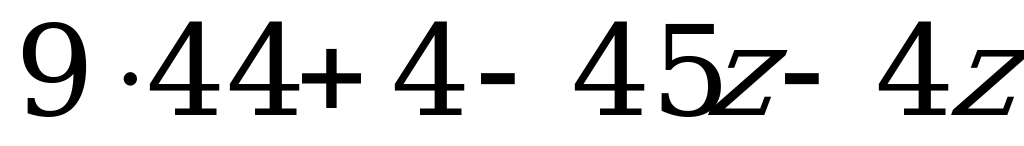 =9(44-5z) + 4(1-z), то это возможно только тогда, когда делится на 9 число 1-z, т.е. когда z = 1.
=9(44-5z) + 4(1-z), то это возможно только тогда, когда делится на 9 число 1-z, т.е. когда z = 1.
Таким образом, z = 1, у = 39, х = 60.
5.Функция f(x) определена при всех действительных значениях х и удовлетворяет при всех 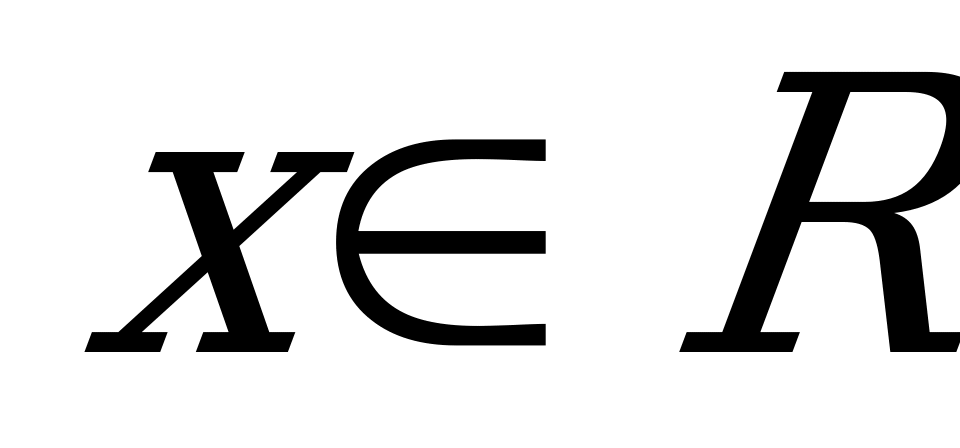 условию 2f (x) + f (1-x) = x2.
условию 2f (x) + f (1-x) = x2.
Найдите f (x).
Решение:
Положим х = 1-у. Тогда данное уравнение
2f (x) + f (x) = x2 (1)
примет вид 2f (1-у) + f (у) = (1-у)2. Последнее уравнение выполняется при всех у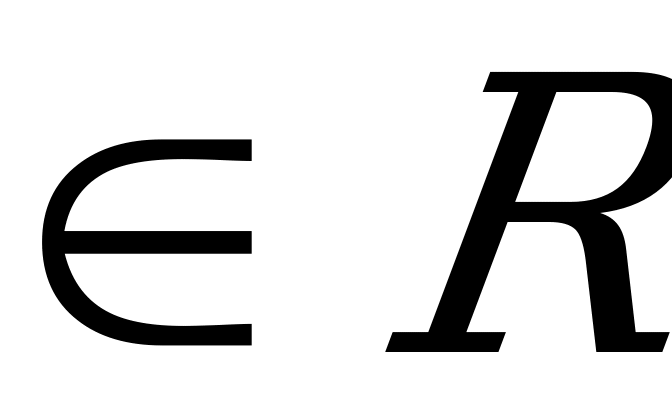 . Заменяя в этом уравнении у на х, получаем уравнение
. Заменяя в этом уравнении у на х, получаем уравнение
2f (1-x) + f (x) = (1-x)2, (2)
вновь содержащее f (x) и f (1-x). Решая систему уравнений (1), (2) как линейную относительно f(x) и f(1-х), находим, что 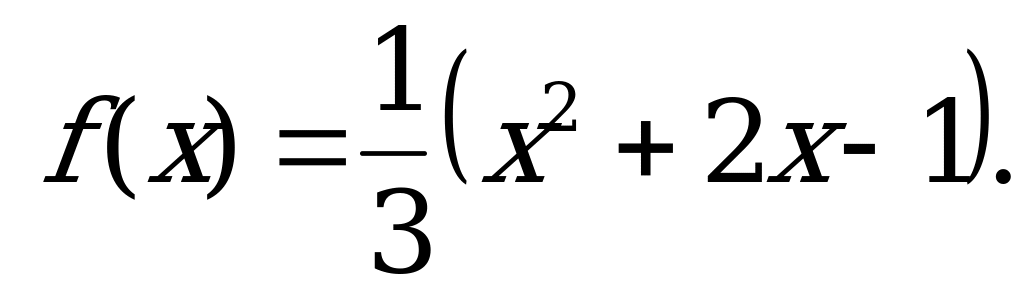 Нетрудно проверить, что найденная функция удовлетворяет функциональному уравнению (1).
Нетрудно проверить, что найденная функция удовлетворяет функциональному уравнению (1).
6.7. 11 класс
1. Известно, что 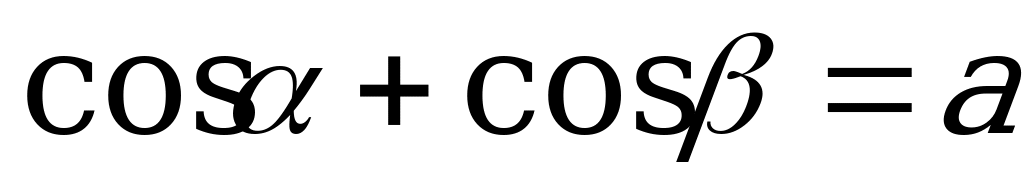 и
и 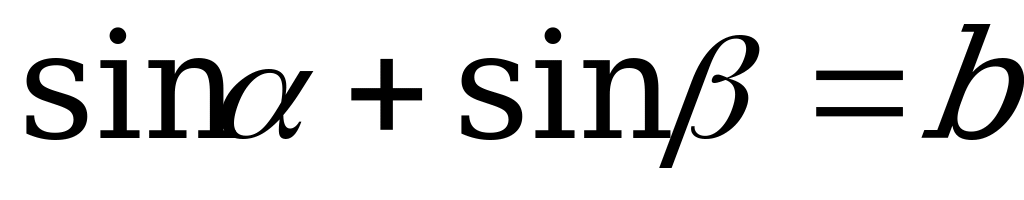 ,
, 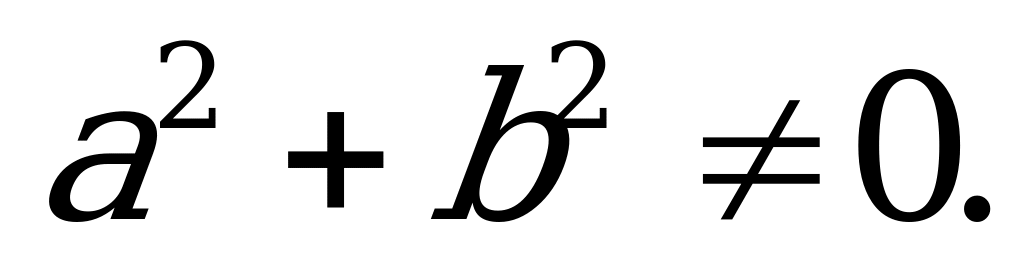 Выразите
Выразите 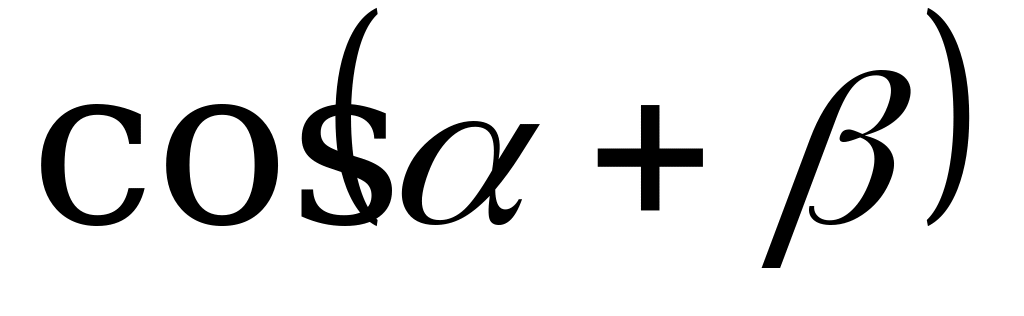 через
через 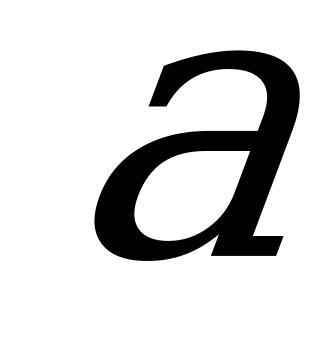 и
и 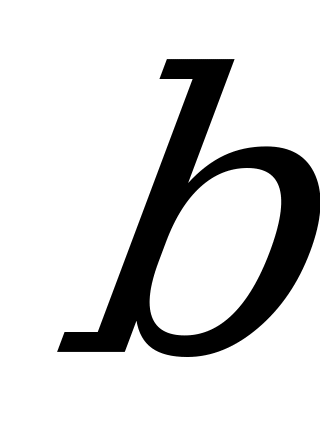 .
.
Решение:
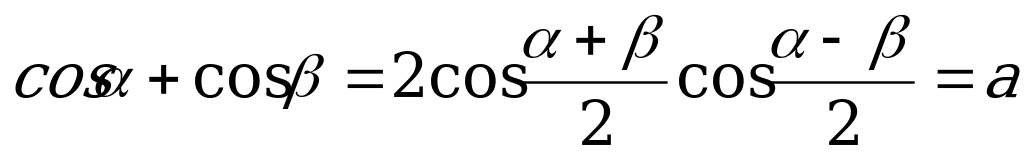 ,
, 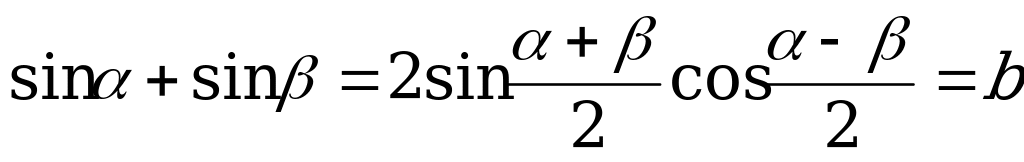 , откуда
, откуда 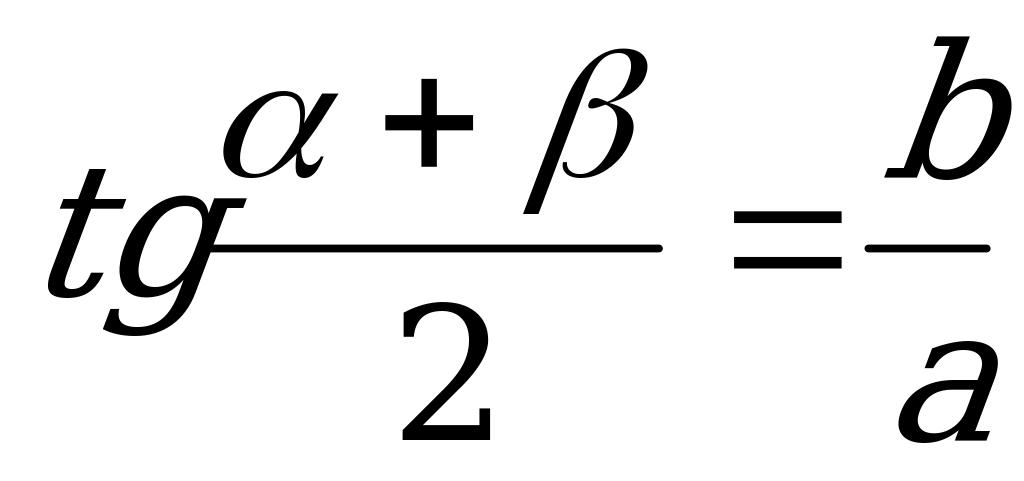 . Осталось воспользоваться формулой
. Осталось воспользоваться формулой
Ответ: 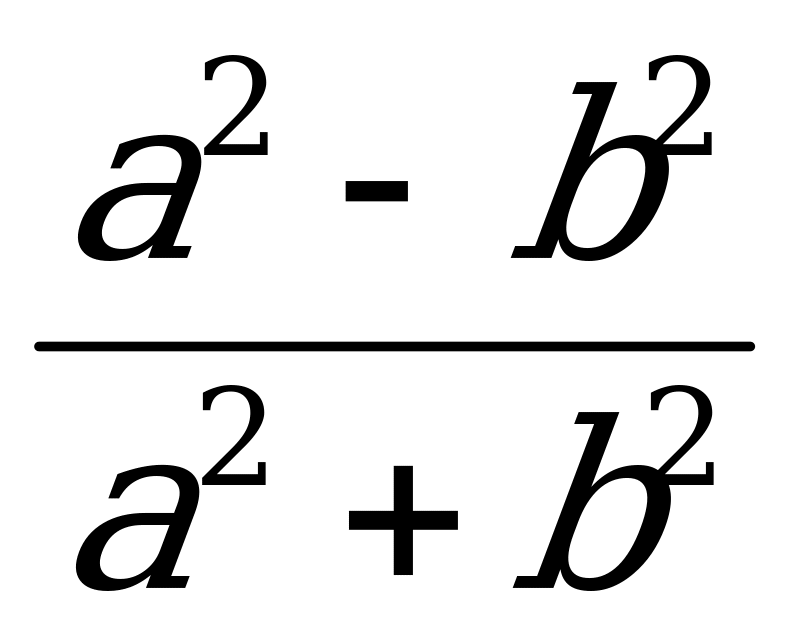 .
.
2. На доске написаны числа 1, 2, 3, …, 10. Какое наименьшее количество чисел нужно стереть с доски так, чтобы оставшиеся числа можно было разбить на две группы с одинаковыми произведениями чисел в группах?
Решение:
Из разложения чисел на простые множители следует, что нужно стереть 7, и в разные группы записать 9 и пару 3, 6, 5 и 10. Искомое разбиение: 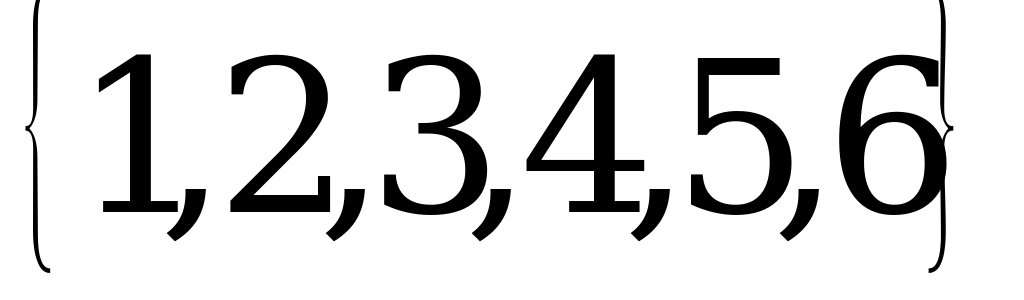 ,
, 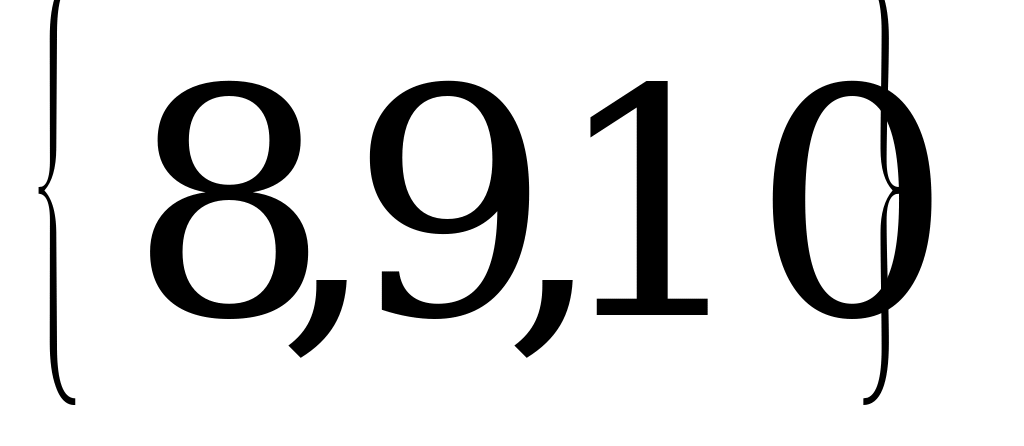 . Здесь
. Здесь 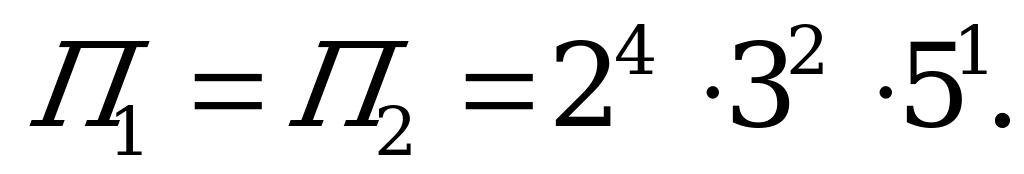
3. В коробке лежат красные, желтые и зеленые карандаши трех размеров: короткие, средние и длинные. Известно, что имеются карандаши всех трех цветов и размеров. Верно ли, что обязательно найдутся три карандаша, попарно различающиеся одновременно и по цвету, и по размеру?
Решение:
Неверно. Например, пусть в коробке лежат 5 карандашей: 3 длинных всех цветов, а также 2 красных: короткий и средний. Тогда среди любых трех попарно различных по размеру карандашей два карандаша будут красными.
Ответ: неверно.
4. Бригады рабочих получили одежду на складе по 2 комплекта на каждого человека. Каждая бригада получила на 20 комплектов больше, чем было бригад. Если бы бригад было на 4 больше и каждой выдавали по 12 комплектов, то одежды на всех не хватило бы. Сколько комплектов было на складе?
Решение:
Пусть было х бригад и в каждой по n рабочих. Тогда число комплектов на бригаду (2n) на 20 больше числа бригад х, т.е. 2n = x + 4 и каждая получила по 12 комплектов., то общее количество комплектов 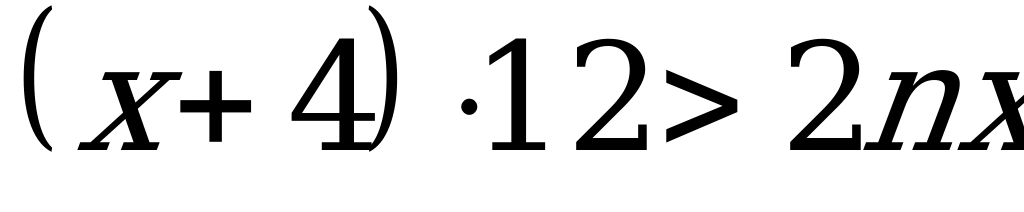 . Это равносильно неравенству
. Это равносильно неравенству 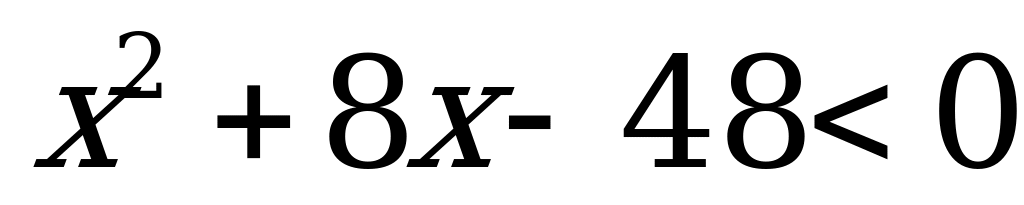 , решением которого являются все х из промежутка (-12,4). С учетом положительности и целочисленности х ограничиваемся лишь тремя натуральными числами: 1, 2, 3.
, решением которого являются все х из промежутка (-12,4). С учетом положительности и целочисленности х ограничиваемся лишь тремя натуральными числами: 1, 2, 3.
Вспомним далее, чо 2n = х + 20, видим, что х = 2n – 20 = 2(n-10), т.е. х – четное число. Из оставшихся трех значений четным является лишь число 2, т.е. n = 11, а общее число комплектов на складе 2nx = 44.
Ответ: 44 комплекта.
5. Окно состоит из прямоугольника, завершенного равносторонним треугольником. Определить отношение высоты прямоугольной части окна к стороне треугольной части так, чтобы при данном периметре окна оно пропускало бы наибольшее количество света.
Решение:
Пусть высота прямоугольной части окна h, а сторона треугольной части a, тогда периметр равен:
P = 2h + 3a,
откуда
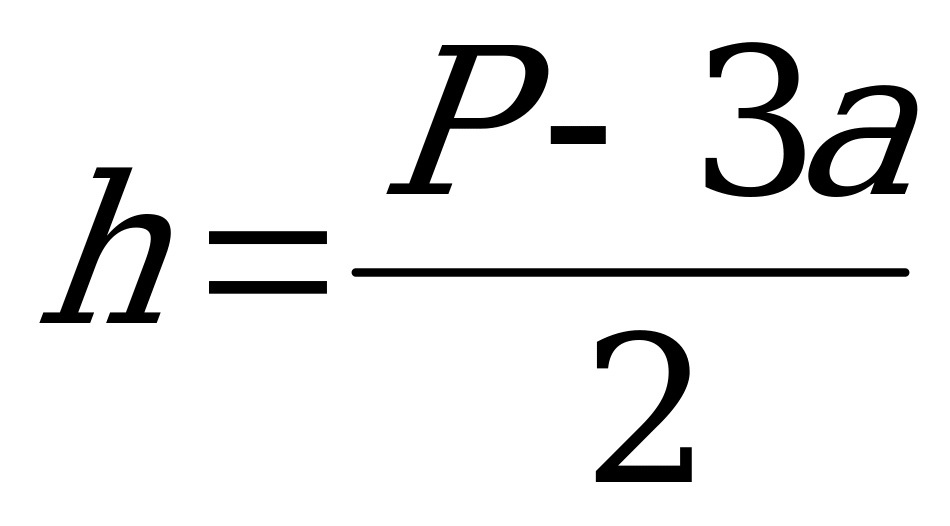 (1).
(1).
Площадь окна 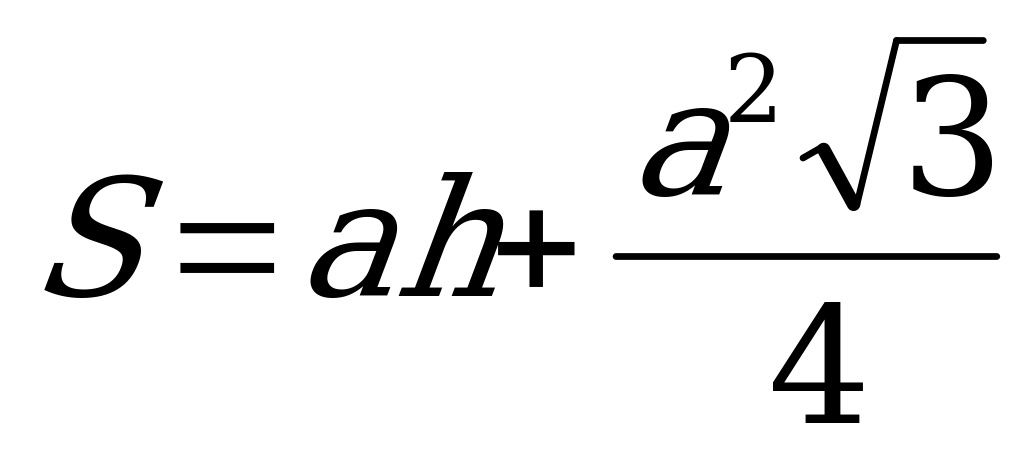 . Учитывая (1), имеем
. Учитывая (1), имеем 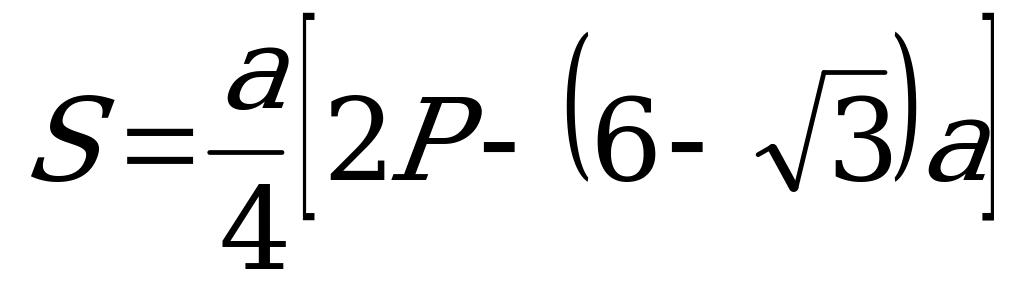 , или
, или 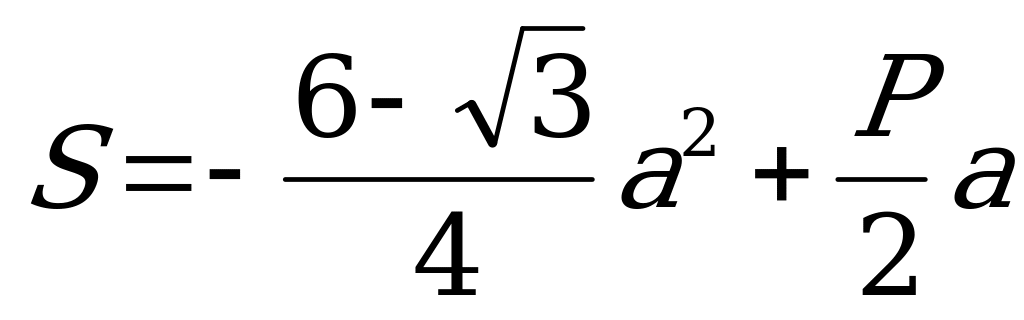 . Итак, S – квадратная функция аргумента a, максимум которой достигается при
. Итак, S – квадратная функция аргумента a, максимум которой достигается при
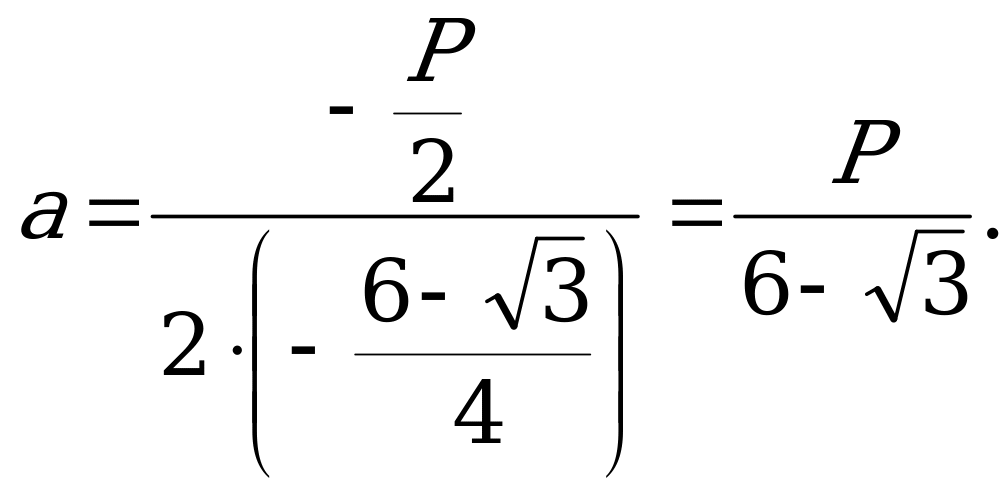 В этом случае
В этом случае 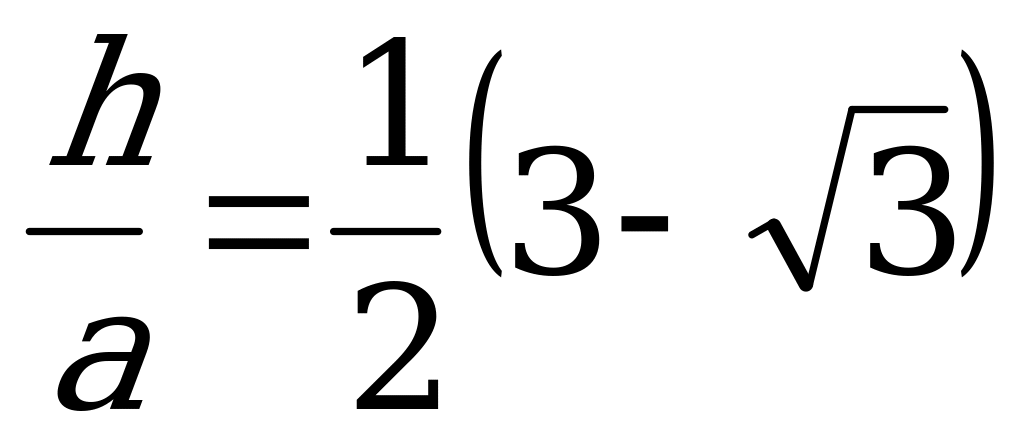 .
.
Рекомендуемая литература
Всероссийские олимпиады школьников по математике 1993–2006: Окружной и финальный этапы /Н. Х. Агаханов и др. Под ред. Н.Х.Агаханова.— М.: МЦНМО, 2007. — 472 с.
Балаян Э.Н. 1001 олимпиадная и занимательная задачи по математике / Э.Н. Балаян. — 3-е изд. — Ростов н/Д : Феникс, 2008. — 364, [1] с.: ил. — (Библиотека учителя).
Горбачёв Н. В. Сборник олимпиадных задач по математике. — М.: МЦНМО, 2004. — 560 с.
Математика в задачах. Сборник материалов выездных школ команды Москвы на Всероссийскую математическую олимпиаду / Под ред. А.А. Заславского, Д.А. Пермякова, А.Б. Скопенкова, М.Б. Скопенкова и А.В. Шаповалова. ਰ М.: МЦНМО, 2009. 488 с.
Канель-Белов А. Я., Ковальджи А. К. Как решают нестандартные задачи / Под ред. В. О. Бугаенко. — 4-е изд. , стереотип. — М. : МЦНМО, 2008. — 96 c.
Московские математические олимпиады 1993—2005 г./ Р.М. Федоров и др. Под ред. В. М. Тихомирова. — М.: МЦНМО, 2006. —456 с.
Для начинающих:
Болл У. , Кокстер Г. Математические эссе и развлечения. — Мир, 1986.
Игнатьев Е. И. В царстве смекалки. — М.: Наука, 1978.
Козлова Е. Г. Сказки и подсказки. Задачи для математического кружка. — М.: МЦНМО, 2004.
Кордемский Б. А. Математическая смекалка. — Юниасм, МДС, 1994.
Произволов В. В. Задачи на вырост. — М.: Бюро Квантум, 2003. — (Приложение к журналу «Квант», № 3, 2003).
Савин А.П. Занимательные математические задачи. — М.: АСТ, 1995.
Спивак А.В. Тысяча и одна задача по математике. — М.: Просвещение, 2002.
Уфнаровский В. А. Математический аквариум. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2000.
Штейнгауз Г. Математический калейдоскоп. — М.: Наука, 1981.
Ященко И. В. Математический праздник. — М.: МЦМНО, 2005.
27






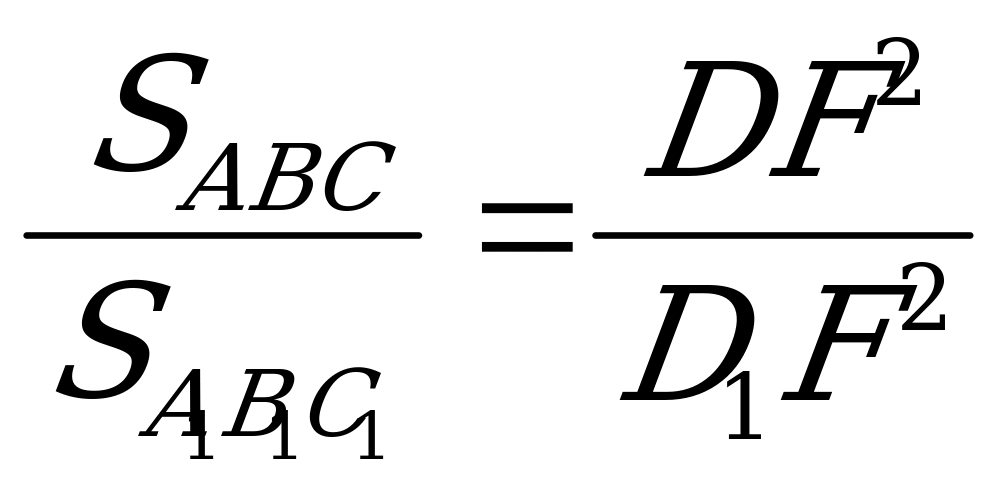 или
или 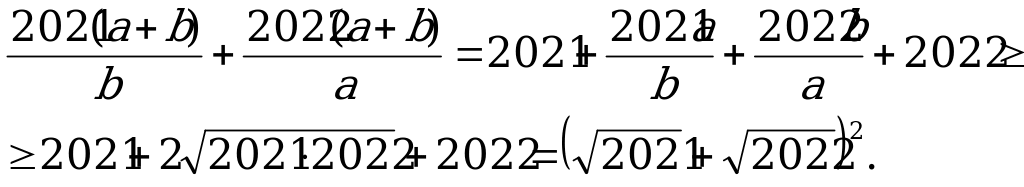
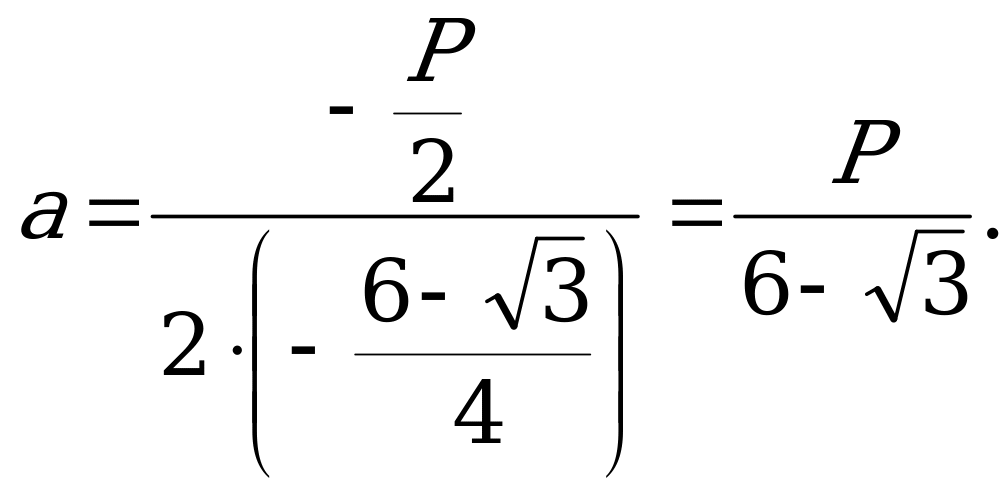 В этом случае
В этом случае 
















