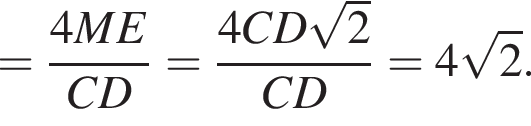Вариант № 12
1. Пользуясь описанием, определите, какими цифрами на плане обозначены деревни. В ответ запишите последовательность четырёх цифр без пробелов, запятых и других дополнительных символов.
| Деревни | Ванютино | Горюново | Егорка | Жилино |
| Цифры |
|
|
|
|
На рисунке изображён план сельской местности.
Таня на летних каникулах приезжает в гости к дедушке в деревню Антоновка (на плане обозначена цифрой 1). В конце каникул дедушка на машине собирается отвезти Таню на автобусную станцию, которая находится в деревне Богданово. Из Антоновки в Богданово можно проехать по просёлочной дороге мимо реки. Есть другой путь — по шоссе до деревни Ванютино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Богданово. Третий маршрут проходит по просёлочной дороге мимо пруда до деревни Горюново, где можно свернуть на шоссе до Богданово. Четвёртый маршрут пролегает по шоссе до деревни Доломино, от Доломино до Горюново по просёлочной дороге мимо конюшни и от Горюново до Богданово по шоссе. Ещё один маршрут проходит по шоссе до деревни Егорка, по просёлочной дороге мимо конюшни от Егорки до Жилино и по шоссе от Жилино до Богданово.
Шоссе и просёлочные дороги образуют прямоугольные треугольники.
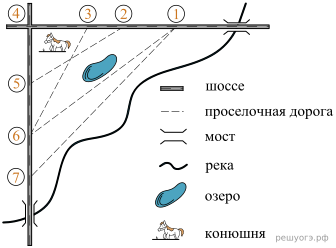
По шоссе Таня с дедушкой едут со скоростью 50 км/ч, а по просёлочным дорогам — со скоростью 30 км/ч. Расстояние от Антоновки до Доломино равно 12 км, от Доломино до Егорки — 4 км, от Егорки до Ванютино — 12 км, от Горюново до Ванютино — 15 км, от Ванютино до Жилино — 9 км, а от Жилино до Богданово — 12 км.
Решение. Пользуясь описанием и рисунком, можно заметить, что деревня Егорка соответствует цифре 2, деревня Доломино — цифре 3, деревня Ванютино — цифре 4, деревня Жилино — цифре 5, деревня Горюново — цифре 6, деревня Богданово — цифре 7.
Ответ: 4625.
2. Найдите расстояние от Антоновки до Егорки по шоссе. Ответ дайте в километрах.
Решение. Расстояние от Антоновки до Доломино состоит из расстояний от Антоновки до Егорки и от Егорки до Доломино, следовательно, расстояние от Антоновки до Егорки равно 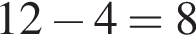 км.
км.
Ответ: 8.
3. Найдите расстояние от Егорки до Жилино по прямой. Ответ дайте в километрах.
Решение. Расстояние от Егорки до Жилино соответствует гипотенузе прямоугольного треугольника с катетами 12 км и 9 км. По теореме Пифагора 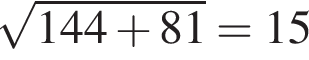 (км.)
(км.)
Ответ: 15.
4. Сколько минут затратят на дорогу Таня с дедушкой из Антоновки в Богданово, если поедут мимо пруда через Горюново?
Решение. Расстояние от Антоновки до Горюнова соответствует гипотенузе треугольника с катетами 20 км и 15 км. Найдем ее по теореме Пифагора: 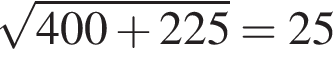 км. По проселочной дороге Таня с дедушкой едут со скоростью 30 км/ч. Следовательно, на путь от Антоновки до Горюново они затратят
км. По проселочной дороге Таня с дедушкой едут со скоростью 30 км/ч. Следовательно, на путь от Антоновки до Горюново они затратят 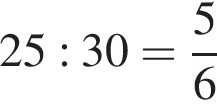 часа или 50 минут. Расстояние от Горюново до Богданово 6 км, скорость по шоссе Тани с дедушкой составляет 50 км/ч. Следовательно, на путь от Горюново до Богданово они затратят
часа или 50 минут. Расстояние от Горюново до Богданово 6 км, скорость по шоссе Тани с дедушкой составляет 50 км/ч. Следовательно, на путь от Горюново до Богданово они затратят  часа или 7,2 минуты. Таким образом, на весь путь Таня с дедушкой затратят
часа или 7,2 минуты. Таким образом, на весь путь Таня с дедушкой затратят 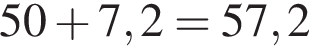 минуты.
минуты.
Ответ: 57,2.
5. На просёлочных дорогах машина дедушки расходует 9,2 литра бензина на 100 км. Известно, что на путь из Антоновки до Богданово через Ванютино, как и на путь через Доломино и Горюново мимо конюшни ей необходим один и тот же объём бензина. Сколько литров бензина на 100 км машина дедушки расходует на шоссе?
Решение. Пусть x литров — расход бензина по шоссе на 100 км. Путь из Антоновки до Богданово через Ванютино проходит полностью по шоссе. Расстояние является суммой расстояний от Антоновки до Ванютино и от Ванютино до Богданово, то есть  Следовательно, бензина будет затрачено
Следовательно, бензина будет затрачено 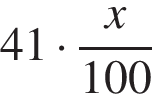 литров.
литров.
Длина пути из Антоновки до Богданово через Доломино и Горюново равна сумме расстояний от Антоновки до Доломино и от Горюново до Богданова  пройденных по шоссе, и расстояния от Доломина до Горюнова
пройденных по шоссе, и расстояния от Доломина до Горюнова 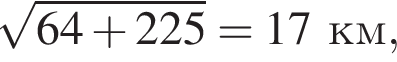 по проселочной дороге. Следовательно, бензина будет затрачено
по проселочной дороге. Следовательно, бензина будет затрачено 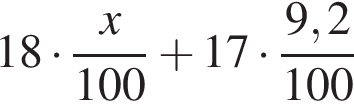 литров.
литров.
Известно, что на оба пути необходим один и тот же объем бензина. Составим и решим уравнение:
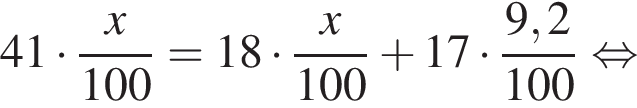
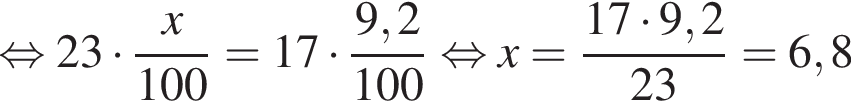 литров на 100 км.
литров на 100 км.
Ответ: 6,8.
6.
Найдите значение выражения 3,8 + 2,9.
Решение. Найдем значение выражения: 3,8 + 2,9 = 6,7.
Ответ: 6,7.
7. На координатной прямой отмечено число 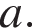
В ответе укажите номер правильного варианта.
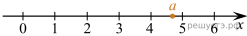
Какое из утверждений относительно этого числа является верным?
1) 
2) 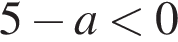
3) 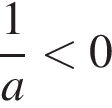
4) 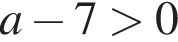
Решение. Заметим, что 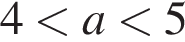 . Проверим все варианты ответа:
. Проверим все варианты ответа:
1) 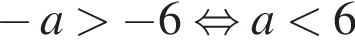 — верно.
— верно.
2) 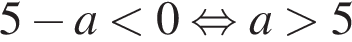 — неверно.
— неверно.
3) 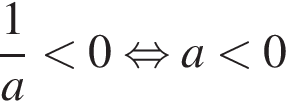 — неверно.
— неверно.
4) 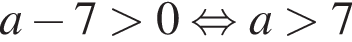 — неверно.
— неверно.
Верным является утверждение 1.
8. Найдите значение выражения 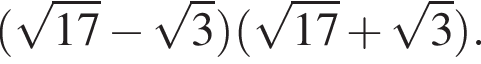
Решение. Последовательно получаем:
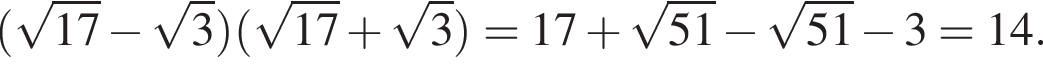
Ответ: 14.
9. Найдите корни уравнения 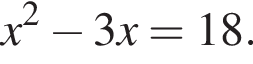
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение. Перенесём всё в уравнении в одну сторону:
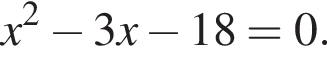
По теореме Виета, сумма корней равна 3, а их произведение равно −18. Тем самым, это числа −3 и 6.
Ответ: −36.
10. Для экзамена подготовили билеты с номерами от 1 до 50. Какова вероятность того, что наугад взятый учеником билет имеет однозначный номер?
Решение. Всего было подготовлено 50 билетов. Среди них 9 были однозначными. Таким образом, вероятность того, что наугад взятый учеником билет имеет однозначный номер равна 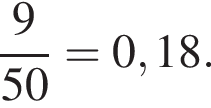
Ответ: 0,18.
11. На рисунке изображён график функции 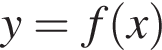 . Какие из утверждений относительно этой функции неверны? Укажите их номера.
. Какие из утверждений относительно этой функции неверны? Укажите их номера.
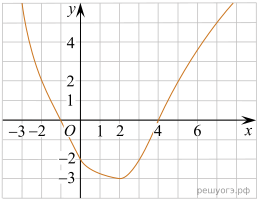
1) функция возрастает на промежутке 
2) 
3) 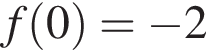
4) прямая  пересекает график в точках
пересекает график в точках 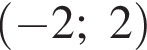 и
и 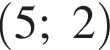
Решение. Проверим каждое из утверждений.
1) Функция возрастает на промежутке  — неверно, функция убывает на промежутке
— неверно, функция убывает на промежутке 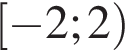 и затем возрастает на
и затем возрастает на  .
.
2)  — неверно,
— неверно, 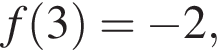
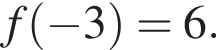
3) 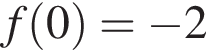 — верно, видно из графика.
— верно, видно из графика.
4) Прямая  пересекает график в точках
пересекает график в точках 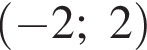 и
и 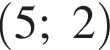 — верно, видно из графика.
— верно, видно из графика.
Таким образом, неверные утверждения находятся под номерами 1 и 2.
Ответ: 12.
12. Закон Менделеева-Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м3), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). Пользуясь этой формулой, найдите объём V (в м3), если T = 250 К, P = 23 891,25 Па, ν = 48,3 моль.
Решение. Выразим объём из закона Клапейрона-Менделеева: 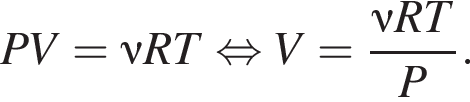 Подставляя, получаем:
Подставляя, получаем:
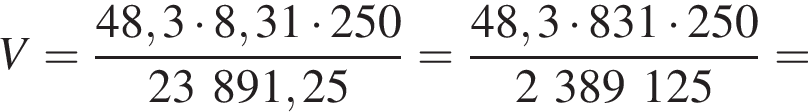
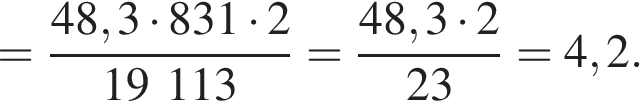
Ответ: 4,2.
13. Укажите решение неравенства 
1)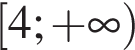
2)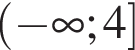
3)
4)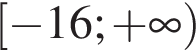
Решение. Последовательно получаем:
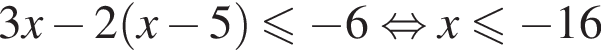
Правильный ответ указан под номером: 3.
Ответ: 3
14. В амфитеатре 12 рядов. В первом ряду 18 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?
Решение. Количества мест в рядах представляют собой арифметическую прогрессию с первым членом 18. Найдем сумму этой прогрессии:
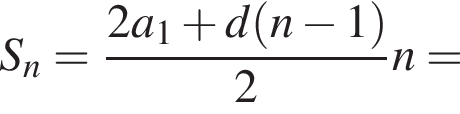
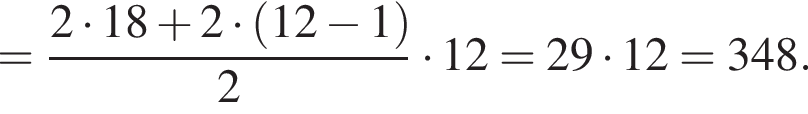
Ответ: 348 мест.
15.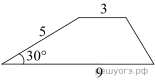
Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Решение. 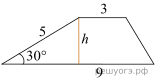 Площадь трапеции вычисляется по формуле
Площадь трапеции вычисляется по формуле
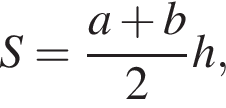 где a и b — основания, а h — высота трапеции. Найдём высоту:
где a и b — основания, а h — высота трапеции. Найдём высоту: 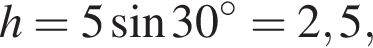 следовательно,
следовательно, 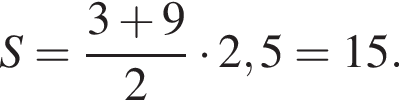
Ответ: 15.
16.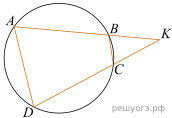
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK = 12, DK = 16, BC = 24. Найдите AD.
Решение. Угол BAD и угол BCD — вписанные углы, опирающиеся на противоположенные дуги.
Следовательно: 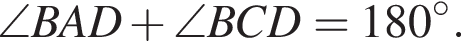
Так как углы BCK и BCD смежные, то 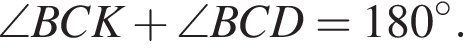
Значит, 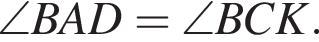
Треугольники AKD и CKB подобны по первому признаку ( и
и 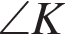 — общий).
— общий).
Следовательно,
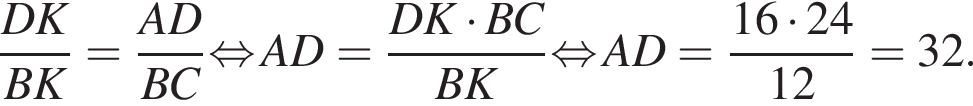
Ответ: 32.
17.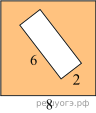
Из квадрата вырезали прямоугольник (см. рис.). Найдите площадь получившейся фигуры.
Решение. Площадь получившейся фигуры равна разности площади квадрата и площади прямоугольника, таким образом:
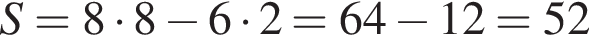 .
.
Ответ: 52.
18.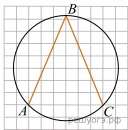
Найдите угол ABC. Ответ дайте в градусах.
Решение. 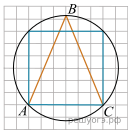 Угол ABC опирается на дугу, которая составляет четверть окружности, т. е. 90°. Так как угол ABC - вписанный, то он равен половине дуги, т. е. 45°
Угол ABC опирается на дугу, которая составляет четверть окружности, т. е. 90°. Так как угол ABC - вписанный, то он равен половине дуги, т. е. 45°
Ответ: 45
19. Какие из следующих утверждений верны?
1) Если две стороны треугольника равны 4 и 5, а угол между ними равен 30°, то площадь этого треугольника равна 10.
2) Площадь трапеции равна произведению суммы оснований на высоту.
3) Площадь трапеции не превосходит произведения средней линии на высоту.
4) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне.
Решение. Проверим каждое из утверждений.
1) «Если две стороны треугольника равны 4 и 5, а угол между ними равен 30°, то площадь этого треугольника равна 10.» — неверно, площадь треугольника равна 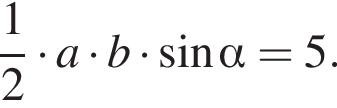
2) «Площадь трапеции равна произведению суммы оснований на высоту.»— неверно, площадь трапеции равна произведению полусуммы оснований на высоту.
3) «Площадь трапеции не превосходит произведения средней линии на высоту.» — верно, площадь трапеции равна произведению средней линии на высоту.
4) «Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне.» — верно, площадь треугольника равна 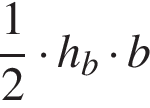
Ответ: 34.
20. Сократите дробь: 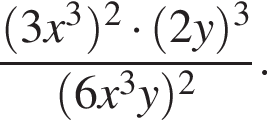
Решение. Имеем:
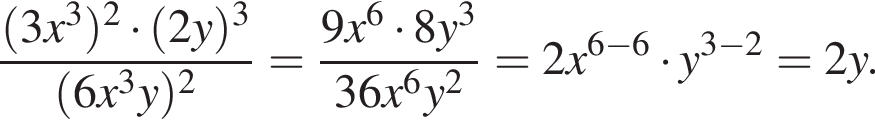
Ответ: 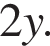
21. Поезд, двигаясь равномерно со скоростью 86 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 6 км/ч, за 18 секунд. Найдите длину поезда в метрах.
Решение. Скорость сближения пешехода и поезда равна 86 − 6 = 80 км/ч. Заметим, что 1 м/c равен 3,6 км/ч. Значит, длина поезда в метрах равна 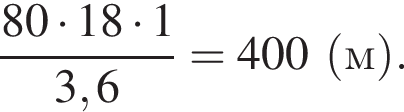
Ответ: 400 м.
22. Постройте график функции
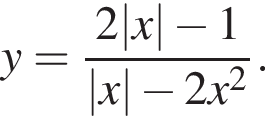
Определите, при каких значениях k прямая y = kx не имеет с графиком общих точек.
Решение. Преобразуем выражение:
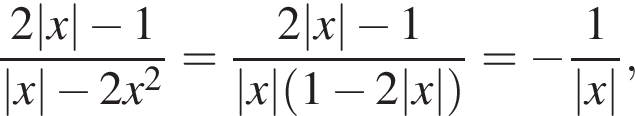
при условии, что 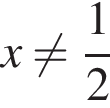 и
и 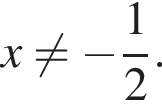
Построим график:
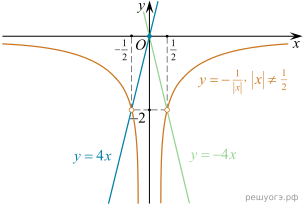
Прямая y = kx не имеет с графиком ни одной общей точки, если она совпадает с осью Ox или если она проходит через точку 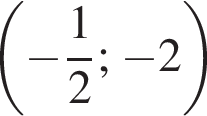 или через точку
или через точку 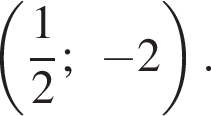 Получаем, что k = −4, k = 0 и k = 4.
Получаем, что k = −4, k = 0 и k = 4.
Ответ: −4; 0; 4.
23. Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 135°, а CD = 29.
Решение. 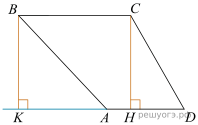 Введём обозначения, как показано на рисунке. Проведём высоты CH и
Введём обозначения, как показано на рисунке. Проведём высоты CH и 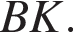 В трапеции сумма смежных углов при боковой стороне равна 180°, поэтому
В трапеции сумма смежных углов при боковой стороне равна 180°, поэтому 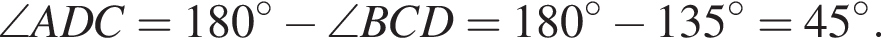 Из прямоугольного треугольника CHD найдём сторону
Из прямоугольного треугольника CHD найдём сторону 
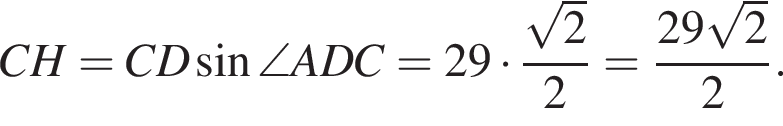
Углы ABC и BAK равны как накрест лежащие углы при параллельных прямых. Высоты CH и BK равны. Из прямоугольного треугольника ABK найдём 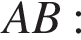
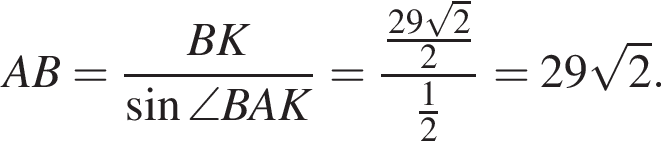
Ответ: 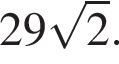
24. В остроугольном треугольнике ABC проведены высоты  и
и 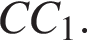 Докажите, что углы
Докажите, что углы 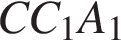 и
и  равны.
равны.
Решение. 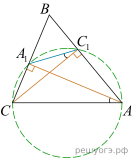 Треугольники
Треугольники 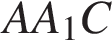 и
и  имеют общую гипотенузу AC. Поэтому точки
имеют общую гипотенузу AC. Поэтому точки 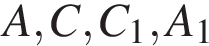 лежат на одной окружности. Углы
лежат на одной окружности. Углы 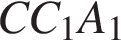 и
и  опираются на одну дугу, и поэтому равны.
опираются на одну дугу, и поэтому равны.
25. В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD = 8, BC = 4.
Решение.  Проведём построения, как показано на рисунке. Расстояние от точки E до прямой CD — отрезок
Проведём построения, как показано на рисунке. Расстояние от точки E до прямой CD — отрезок 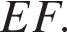 Продолжим стороны AB и CD до пересечения в точке M, проведём отрезок CK, параллельный
Продолжим стороны AB и CD до пересечения в точке M, проведём отрезок CK, параллельный  Рассмотрим четырёхугольник ABCK прямая
Рассмотрим четырёхугольник ABCK прямая  параллельна
параллельна 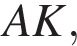 прямая
прямая 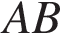 параллельна прямой CK, угол BAK — прямой, следовательно, ABCK — прямоугольник. Откуда
параллельна прямой CK, угол BAK — прямой, следовательно, ABCK — прямоугольник. Откуда 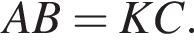 Значит,
Значит, 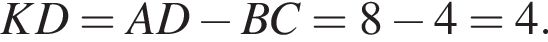 Из прямоугольного треугольника
Из прямоугольного треугольника 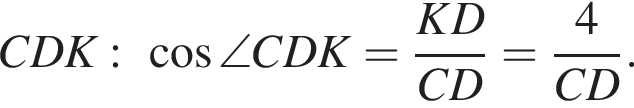 Рассмотрим треугольники MCB и CKD, они прямоугольные, углы DMA и DCK равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны:
Рассмотрим треугольники MCB и CKD, они прямоугольные, углы DMA и DCK равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны:
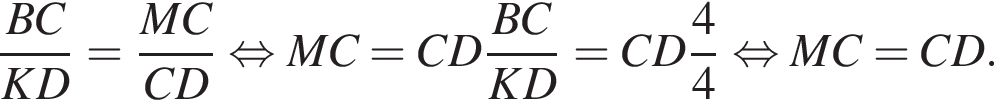
По теореме о касательной и секущей:
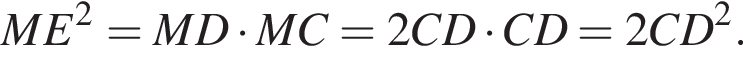
Откуда  Рассмотрим треугольники MEF и MAD, они прямоугольные, угол BMC — общий, следовательно, эти треугольники подобны. Значит, углы MEF и ADM равны, а значит,
Рассмотрим треугольники MEF и MAD, они прямоугольные, угол BMC — общий, следовательно, эти треугольники подобны. Значит, углы MEF и ADM равны, а значит,  Найдём EF из прямоугольного треугольника
Найдём EF из прямоугольного треугольника 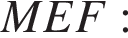
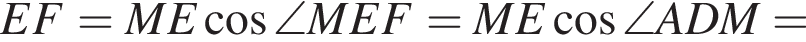
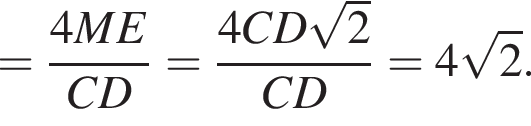
Ответ: 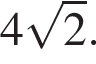
| № задания | ответ |
| 1 | 4625 |
| 2 | 8 |
| 3 | 15 |
| 4 | 57,2 |
| 5 | 6,8 |
| 6 | 6,7 |
| 7 | 1 |
| 8 | 14 |
| 9 | -36 |
| 10 | 0,18 |
| 11 | 12 |
| 12 | 4,2 |
| 13 | 3 |
| 14 | 348 |
| 15 | 15 |
| 16 | 32 |
| 17 | 52 |
| 18 | 45 |
| 19 | 34 |
| 20 | 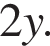
|
| 21 | 400 |
| 22 | −4; 0; 4 |
| 23 | 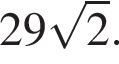
|
| 24 | - |
| 25 | 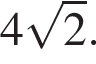
|









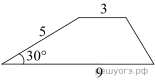
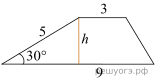 Площадь трапеции вычисляется по формуле
Площадь трапеции вычисляется по формуле


 Угол ABC опирается на дугу, которая составляет четверть окружности, т. е. 90°. Так как угол ABC - вписанный, то он равен половине дуги, т. е. 45°
Угол ABC опирается на дугу, которая составляет четверть окружности, т. е. 90°. Так как угол ABC - вписанный, то он равен половине дуги, т. е. 45°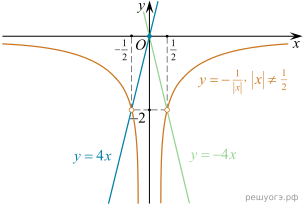
 Введём обозначения, как показано на рисунке. Проведём высоты CH и
Введём обозначения, как показано на рисунке. Проведём высоты CH и 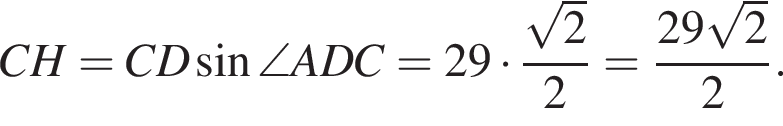
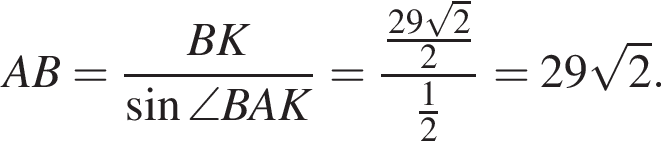
 Треугольники
Треугольники  Проведём построения, как показано на рисунке. Расстояние от точки E до прямой CD — отрезок
Проведём построения, как показано на рисунке. Расстояние от точки E до прямой CD — отрезок