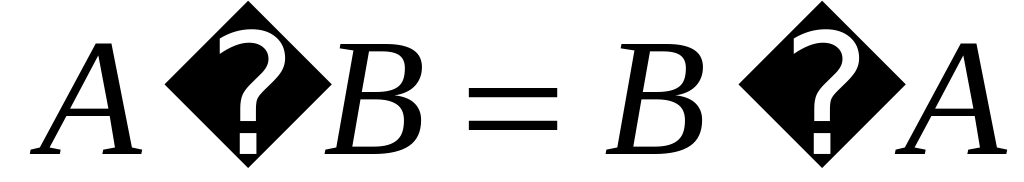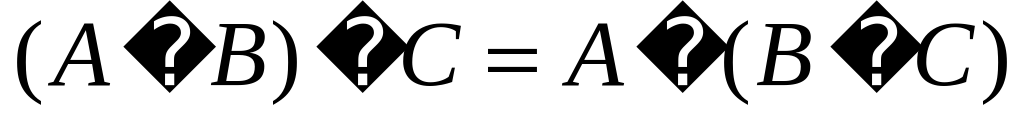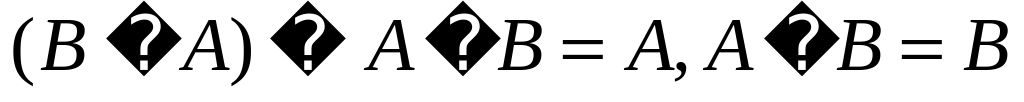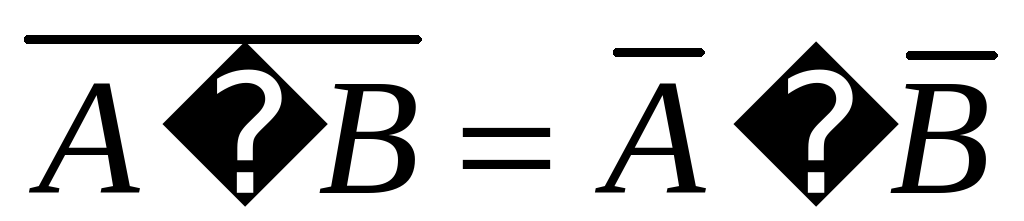18
Тема 12. Элементы дискретной математики
(6 аудиторных часов+2 часа к.р.)
ЛЕКЦИЯ 2/1. ОСНОВНЫЕ ПОНЯТИЯ ДИСКРЕТНОЙ МАТЕМАТИКИ
Введение – 7 мин.
1. Множества и операции над ними – 40 мин.
2. Основные элементы и правила комбинаторики – 40 мин.
Заключение – 3 мин.
Введение
Различные разделы математики, дискретная математика, ее основные разделы: теория множеств, комбинаторика, теория графов.
1. Множества и операции над ними
Само множество является первичным математическим понятием, которое не определяется, а может быть лишь описано или пояснено с помощью примеров.
Обычно под множеством понимают совокупность или набор каких-либо предметов, объектов и т.п., называемых элементами множества, обладающих некоторым характеристическим свойством.
Если рассматриваемый объект обладает этим свойством, его включают в данное множество, если не обладает, то не включают.
Примерами множеств являются: множество студентов университета, множество предприятий некоторой отрасли, множество вещественных чисел и т.д.
Множества будем обозначать большими буквами латинского алфавита: А, В, С, …X, Y,…, а элементы множеств – малыми буквами: a, b, c, …, x, y,…
Если а является элементом множества А, то пишут аÎА (читается "а принадлежит множеству А"). Если же а не принадлежит множеству А, то пишут аÏА.
Запись А = {a, b, c, …} означает, что множество А состоит из элементов a, b, c и других, заданных тем же способом.
Если множество А состоит из элементов ар, где р пробегает множество индексов Р, то будем писать А = {aр}рÎР, или просто А = {aр}.
Из школьного курса известны следующие числовые множества:
R – множество вещественных (действительных) чисел;
I – множество иррациональных чисел,
Q – множество рациональных чисел;
Z – множество целых чисел;
N – множество натуральных чисел.
Множества А и В называются равными (А=В), если они состоят из одних и тех же элементов.
Для удобства вводится понятие пустого множества, которое обозначается символом Æ. Множество, не содержащее ни одного элемента, называется пустым. Например, пустым является множество вещественных корней уравнения х2+2=0.
Если каждый элемент множества А является элементом множества В, то говорят, что множество А является подмножеством множества В, или, что множество В содержит множество А.
Если множество В содержит множество А, но не равно ему, то записывают АÌВ, если допускается и равенство множеств, то записывают АÍВ. Например, если А - множество натуральных чисел, а В – множество вещественных, то А является подмножеством В. Из определения подмножества следует, что АÍА, каково бы ни было множество А. Кроме этого, принято считать, по определению, что пустое множество является подмножеством каждого множества, т.е. ÆÌА.
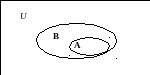
Множества и их различные комбинации можно представлять графически в виде диаграмм Эйлера-Венна.
Диаграммы Эйлера-Венна – геометрические представления множеств.
Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.
Условие АÌВ графически (в виде диаграммы Эйлера-Венна) можно представить следующим образом:
Над множествами можно проводить некоторые операции, подобные арифметическим действиям с числами. Операции над множествами рассматриваются для получения новых множеств из уже существующих.
Пусть А и В - некоторые произвольные множества.
Объединением (или суммой) множеств А и В называется множество АÈВ, состоящее из тех и только тех элементов, которые содержатся хотя бы в одном из множеств А, В:

Таким образом, если элемент принадлежит множеству АÈВ, то он принадлежит либо множеству А, либо множеству В, либо обоим этим множествам.
Пересечением множеств А и В называется множество АÇВ, состоящее из тех и только тех элементов, которые содержатся одновременно и в множестве А и в множестве В:
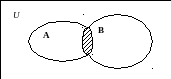

Аналогично определяется пересечение и объединение любого конечного числа множеств.
Р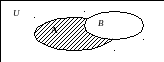 азностью между множеством А и множеством В называется множество А\В, состоящее из элементов, принадлежащих множеству А, но не принадлежащих множеству В:
азностью между множеством А и множеством В называется множество А\В, состоящее из элементов, принадлежащих множеству А, но не принадлежащих множеству В:
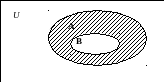
Если ВÌА, то разность А\В называется дополнением `В множества В до множества А или дополнением В в А:
Пример. Пусть даны множества А={1,5,7,8,9}; В={2,5,6,7} и С={1,5}. Найти АÈВ, АÇВ, А\В, `С - дополнение С в А.
Решение. АÈВ={1, 2, 5, 6, 7, 8, 9};
АÇВ={5, 7};
А\В={1, 8, 9};
`С={7, 8, 9}.
Операции над множествами обладают следующими свойствами:
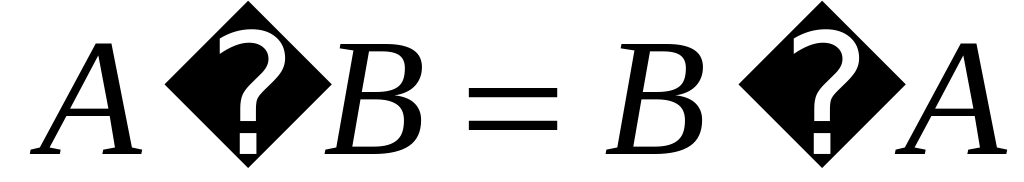
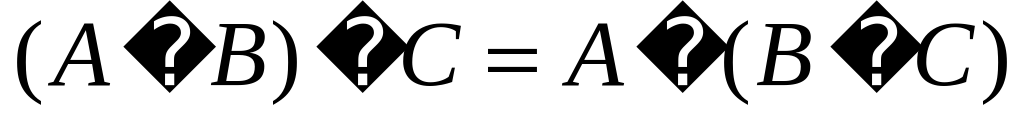


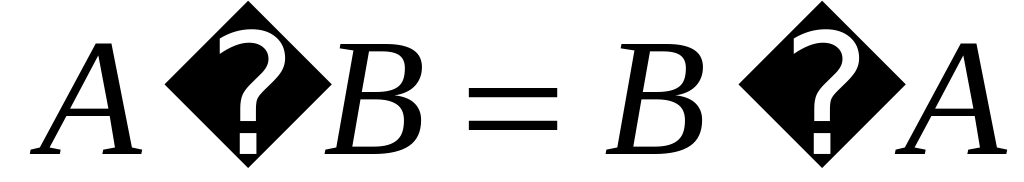
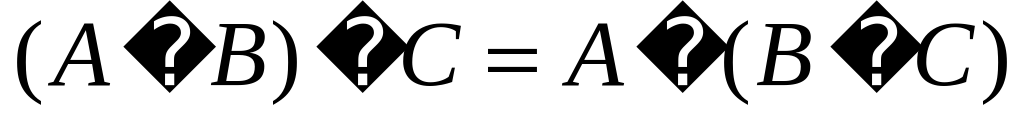

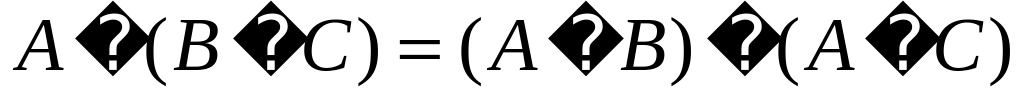
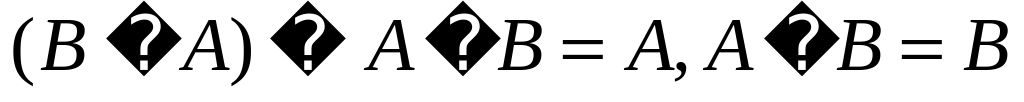
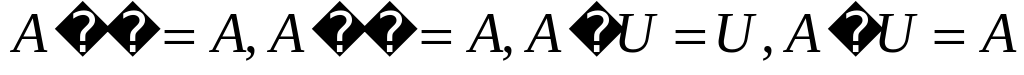

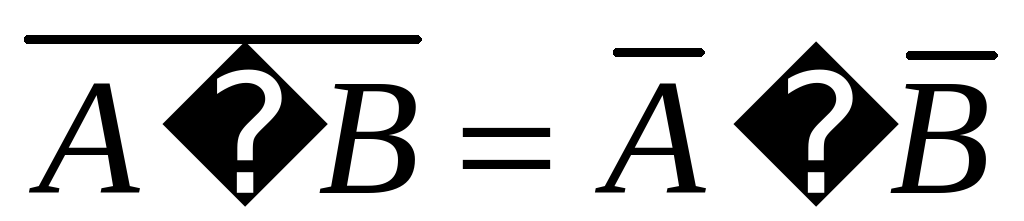
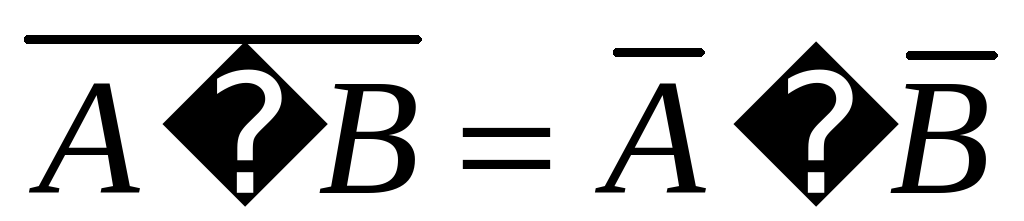
Последние два равенства носят название законов де Моргана.
Для множеств существует операция, называемая декартовым произведением. Пусть множество A состоит из p элементов, а множество B состоит из q элементов. Составим новое множество A × B, состоящее из всех упорядоченных пар (a, b), где aÎA и bÎ B. Очевидно, что множество A × B содержит pq элементов.
Декартовым произведением множеств А и В называется множество A × B всех упорядоченных пар элементов (a, b), из которых aÎA и bÎ B.
Порядок следования пар может быть любым, но расположение элементов в каждой паре определяется порядком следования перемножаемых элементов. Отсюда очевидно, что для разных множеств  .
.
Понятие декартова произведение можно обобщить на случай любого конечного числа множеств.
Кроме самих элементов, каждое множество характеризуется числом всех элементов, принадлежащих множеству, которое называется мощностью множества. Однако для строго определения этого понятия необходимо рассмотреть два вида множеств.
Мощностью конечного множества (множества, содержащего конечное число элементов) называется количество его элементов. Мощность множества A обозначается m (A)
Например, мощность множества A = {1, 3, 5, 7, 9} равна m (A) = 5.
Ясно, что понятие мощности конечных множеств позволяет сравнивать их по количеству элементов.
Так, если A = {1, 3, 5, 7, 9}, а B = {2, 4, 6, 8}, то m (A) = 5, а m (B) = 4 и потому m (A) m (B).
Однако если мы имеем дело с бесконечными множествами, то пересчитать элементы множества уже не удастся. Чтобы получить возможность описывать количество элементов в бесконечных множествах, введём следующие определения.
Между множествами А и В установлено взаимно-однозначное соответствие, если каждому элементу множества А каким-либо образом сопоставлен единственный элемент множества В, при этом каждому элементу множества В сопоставляется единственный элемент множества А.
Множества, между которыми установлено взаимно однозначное соответствие, содержат одинаковое количество элементов.
Множества, между которыми можно установить взаимно-однозначное соответствие, называются равномощными (имеющими одинаковую мощность, эквивалентными).
Равномощность множеств обозначается символом "~": А ~ В.
Предложенное выше определение справедливо и для конечных множеств.
Рассмотрим два конечных множества: А={-2, 0, 3,8} и В={с, х, ф, а}. Понятно, что m (A) = 4 и m (B) = 4, следовательно, А ~ В. По другому определению для этих множеств можно указать, например, следующее взаимно-однозначное соответствие:
-2 ↔ с, 0 ↔ ф, 3 ↔ а, 8 ↔ х.
Таким образом, А ~ В.
Приведем пример равномощных множеств, состоящих их бесконечного числа элементов. Рассмотрим множество N натуральных чисел и множество N2 = {2, 4, 6, …} четных чисел. Взаимно-однозначное соответствие между этими множествами устанавливается соотношениями n ↔ 2n, следовательно, эти множества равномощны: N ~ N2. Этот пример показывает, что собственное подмножество может быть равномощным всему множеству; естественно, это может быть только для бесконечных множеств.
Соотношение эквивалентности множеств транзитивно: если А ~ В, В ~ С, то А ~ С. Взаимно-однозначное соответствие между элементами а и с множеств А и С устанавливается по цепочке а ↔ в ↔ с.
2. Основные элементы и правила комбинаторики
В процессе своей деятельности человеку иногда приходится иметь дело с задачами, в которых нужно подсчитать число всех возможных способов расположения некоторых предметов или число всех возможных способов осуществления некоторых действий. Задачи такого типа и подобные им называются комбинаторными.
Комбинациями или соединениями назовем группы, составленные из каких-либо предметов или элементов, например, букв, чисел, людей, предприятий и т.д.
Комбинаторика – это раздел математики, изучающий вопросы о том, сколько комбинаций (соединений) определенного вида можно составить из данных элементов.
Основными правилами комбинаторики являются правило сложения (суммы) и правило умножения (произведения).
Рассмотрим правило умножения, на примере следующей задачи.
Из города А в город В можно добраться теплоходом, автобусом, самолетом или поездом. Из города В в город С можно добраться поездом, самолетом, либо автобусом. Сколькими способами можно осуществить путешествие из А в С.
Рассмотрим схему:
|
А | Теплоход Автобус Самолет Поезд |
В | Автобус Самолет Поезд |
С |
Из А в В можно добраться четырьмя видами транспорта, т.е. четырьмя способами. Каждый из этих способов может быть использован с каждым из трех способов переезда из В в С. Отсюда легко получить, что существует 4·3=12 различных способов путешествия из А в С.
Соображения, которые были приведены при решении примера, лежат в основе следующего правила комбинаторики.
Правило умножения. Предположим, что требуется выполнить одно за другим k действий. Если первое действие можно выполнить n1 способами, второе n2 способами, третье n3 способами и так до k-го действия, которое может быть выполнено nk способами, то все k действий вместе могут быть выполнены числом способов, равным n1 · n2 · n3 · … · nk.
Пример. В первой группе учится 20 человек, во второй – 25 человек. Для участия в конференции необходимо выбрать по одному человеку из каждой группы. Сколькими способами это можно сделать?
Решение. Из 20 учащихся первой группы может быть выбран любой, т.е. первое действие может быть совершено 20 способами. Аналогично из 25 учащихся второй группы также может быть выбран любой, т.е. второе действие может быть выполнено 25 способами.
Следовательно, по правилу умножения оба действия, выбор из первой и второй групп по одному человеку, могут быть осуществлены 20·25=500 способами. ■
Изменим условие примера и посмотрим, каким окажется его решение.
Пример. В первой группе учится 20 человек, во второй – 25 человек. Произвольно выбирают одного человека из какой-то группы. Сколькими разными способами это можно сделать?
Решение. Из первой группы человека можно выбрать 20 способами, из второй группы 25 способами. Всего способов 20+25=45.
При решении примера существенным оказывается то, что оба действия (выбор человека из первой и выбор человека из второй группы) не могут быть выполнены одновременно, поскольку они взаимно исключают друг друга. В данном случае должно быть выполнено либо первое действие, либо второе, а не первое, а затем второе.
Рассуждения при решении второго примера лежат в основе второго правила комбинаторики.
Правило сложения. Если два действия взаимно исключают друг друга, причем одно из них может быть выполнено т1 способами, а другое − т2 способами, то выполнить одно любое из этих действий можно т1 + т2 способами.
Это правило легко обобщается на любое конечное число действий.
Комбинации элементов могут быть составлены различными способами, а именно, в виде перестановок, размещений и сочетаний. Прежде чем перейти к рассмотрению этих понятий, познакомимся с понятием факториала натурального числа.
Факториалом натурального числа n называется произведение всех натуральных чисел до n включительно, т.е.
 .
.
Например, 1!=1
2!= 1·2=2
3!= 1·2·3=6
4!= 1·2·3·4=24 и т.д.
По определению принято, что 0!=1.
Пусть имеется три различных элемента a, b, c. Будем составлять из этих элементов различные комбинации.
1. Размещения
Выберем из трех элементов a, b, c два элемента с учетом их расположения. Получим
a b, b a, b c, c b, a c, c a.
Составленные комбинации называются размещениями из трех элементов по два.
Размещениями из n элементов по т в каждом называются такие комбинации из т элементов, взятых из n элементов, которые отличаются друг от друга либо самими элементами, либо порядком их расположения.
Например, размещения a b и b a отличаются порядком расположения элементов, а размещения a b и c b отличаются элементами a и c.
Очевидно, что т ≤ n.
На практике чаще представляют интерес не сами размещения, а их число.
Число размещений из n элементов по т может быть вычислено по следующей формуле
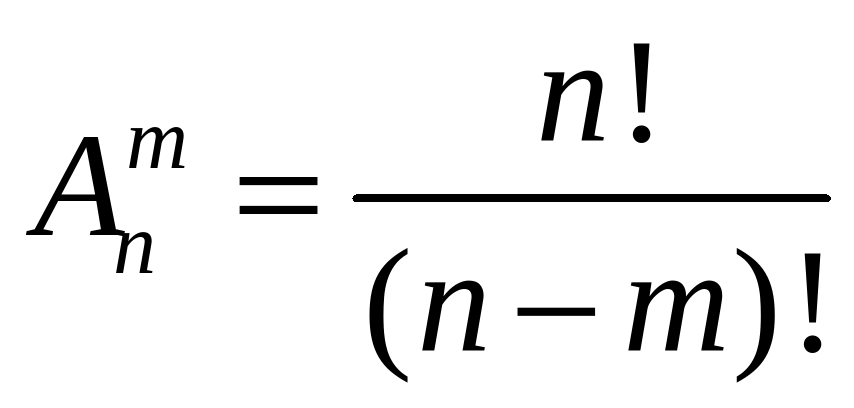 .
.
Пример Руководство некоторого банка должно выбрать трех человек из 12 на три различные должности. Все 12 кандидатов имеют равные шансы на занятие той или иной должности. Сколько существует всевозможных вариантов для выбора?
Решение. Число всевозможных вариантов выбора равно числу размещений из 12 человек по три. Очевидно, что комбинации, состоящие из трех человек, будут размещениями, так как они будут отличаться либо самими людьми, либо расположением этих людей соответственно их должностям (по условию примера – должности разные). Таким образом, число размещений из 12 человек по 3 равно 12·11·10=1320.
В условии предыдущего примера предполагалось, что  . Рассмотрим отдельно случай, когда
. Рассмотрим отдельно случай, когда 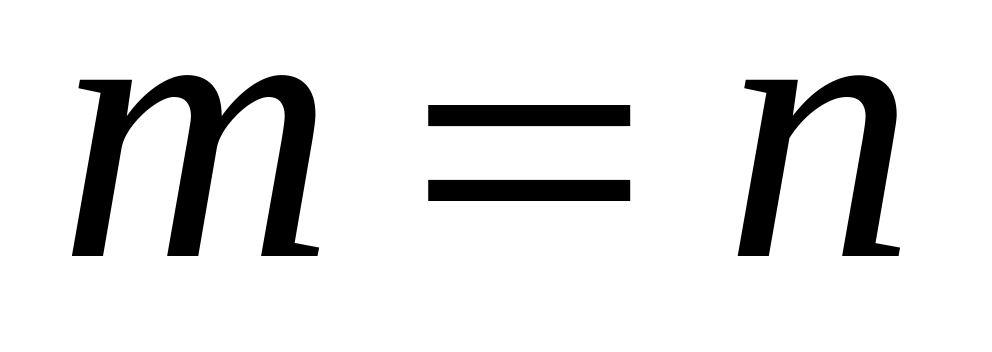 . Соответствующие этому случаю размещения называются перестановками.
. Соответствующие этому случаю размещения называются перестановками.
2. Перестановки
Выберем из трех элементов a, b, c три элемента с учетом их расположения. Получим
a b с, b a с, b c а, c b а, a c b, c a b.
Составленные комбинации называются перестановками из трех элементов.
Перестановками из n элементов называются комбинации, которые состоят из всех n элементов и отличаются лишь порядком расположения этих элементов.
Иначе, перестановки – это размещения из n элементов по n.
Число перестановок из n различных элементов равно
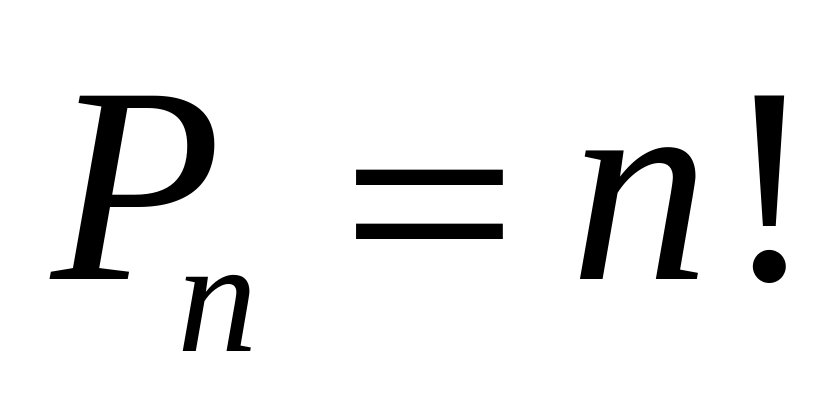
Пример. Представитель торговой фирмы ежедневно просматривает 4 изданий, в которых исследуется спрос и предложение на определенные товары. Сколько существует способов просмотра, если выбор изданий случаен?
Решение. Каждый день все 4 изданий должны быть просмотрены, может меняться лишь порядок просмотра, поэтому число способов просмотра равно .
Рассмотрим два различных размещения, которые состоят из одних и тех же элементов. Тогда они обязательно должны отличаться порядком расположения этих элементов.
Однако часто бывает, что нет необходимости учитывать этот порядок, т.е. размещения, которые отличаются лишь расположением элементов считать равными.
3. Сочетания
Выберем из трех элементов a, b, c два элемента без учета их расположения. Получим
a b, b c, a c.
Составленные комбинации называются сочетаниями из трех элементов по два.
Сочетаниями из n элементов по т в каждом называются такие комбинации т элементов, взятых из n элементов, которые отличаются друг от друга по крайней мере одним элементом.
Очевидно, что т ≤ n.
Число сочетаний из n элементов по т определяется по следующей формуле
где .
Решим рассмотренную выше задачу несколько изменив условие.
Пример. Руководство некоторого банка должно выбрать трех человек из 12 на три одинаковые должности. Все 12 кандидатов имеют равные шансы на занятие той или иной должности. Сколько существует всевозможных вариантов для выбора?
Решение. В виду того, что должности одинаковые, то порядок выбора кандидатов значения не имеет, поэтому при решении применяем формулу для числа сочетаний, получаем
.
Числа называются биномиальными коэффициентами, так как они входят в разложение формулы бинома Ньютона:
.
Числа обладают следующими свойствами:
1) ;
2) ;
3) , где т=0, 1, …, n, удобно применять при ;
4) , где т=0, 1, …, n−1.









 азностью между множеством А и множеством В называется множество А\В, состоящее из элементов, принадлежащих множеству А, но не принадлежащих множеству В:
азностью между множеством А и множеством В называется множество А\В, состоящее из элементов, принадлежащих множеству А, но не принадлежащих множеству В: