«Расскажи ребёнку – услышит,
покажи - увидит,
дай потрогать – поймёт..»
Тема проекта: Формирование пространственного мышления учащихся 5 – 6 классов посредством применения моделей геометрических тел и их конструирования.
Целью работы является разработка системы практических занятий для учащихся 5-6 классов по формированию пространственного мышления.
Задачи проекта:
-
Формирование у учащихся основных геометрических понятий;
-
Создание условий для подготовки учащихся к изучению систематического курса геометрии;
-
Развитие конструктивных умений и навыков посредством: развития мыслительных операций, развития чертежных навыков, конструирования;
-
Развитие пространственного воображения; развитие мелкой моторики, необходимой для успешного обучения;
-
Развитие памяти, внимания, воображения, наблюдательности.
Объектом исследования является пространственное мышление учащихся.
Предмет исследования – процесс формирования пространственного мышления в 5 – 6 классах.
Методы:
-
Изучение и анализ психолого-педагогических и методических источников по теме работы;
-
Методы педагогических исследований: наблюдение, беседа, тестирование, анкетирование учащихся;
-
Экспериментальные методы: организация и проведение опытного обучения; проведение контрольных срезов с целью выявления уровня развития пространственного мышления учащихся; анализ результатов педагогического эксперимента.
Известно, что основные трудности при изучении математики в школе возникают в ходе изучения геометрии. Связано это с тем, что недостаточно развито пространственное воображение, что затрудняет выполнение чертежа.
Для развития пространственного воображения на уроках геометрии я использую различные модели геометрических тел.
Работа с моделями не только помогает ученику представить форму, но развить пространственное мышление. После работы с моделями учащиеся лучше строят и конструируют на плоскости.
Модели изготавливают дети самостоятельно, под моим руководством на дополнительных занятиях или дома. Изготовление и применение моделей геометрических тел позволяет повысить познавательный интерес, доступность изложения и усвоения нового материала, способствует укреплению сотрудничества учителя с учениками. За каждую модель выставляется оценка в журнал. Таким образом, для кабинета математики, силами учеников, изготовлено много различных моделей, как каркасных, так и поверхностных из картона.
Изготовленные модели применяются на уроках геометрии в старших классах и для изучения наглядной геометрии в 5-6 классах.
Они позволяют определить площадь поверхности, объем, выполнить измерения длин, углов и его элементов.
Применяются модели при объяснении нового материала, проверке домашнего задания; при проведении лабораторных и практических работ на нахождение площадей и объемов геометрических тел в старших классах, а также при изучении наглядной геометрии в 5-6 классах.
Сегодня хочу вам показать применение различных моделей при изучении математики в 5-6 классах в виде практических работ.
-
Место темы в системе знаний по предмету
Согласно учебному плану в 5–6 классах изучается интегрированный предмет «Математика», который включает арифметический материал и наглядную геометрию. На изучение наглядной геометрии в курсе:
- 5 класса отводится 31ч., в том числе тема «Фигуры в пространстве» 9ч.;
- 6 класса – 28ч., в том числе тема «Фигуры в пространстве» 7ч.
Содержание обучения.
5 класс. Наглядные представления о пространственных фигурах: прямоугольный параллелепипед, куб, многогранники. Изображение простейших многогранников. Развёртки куба и параллелепипеда. Создание моделей многогранников (из бумаги, проволоки, пластилина и других материалов). Объём прямоугольного параллелепипеда, куба. Единицы измерения объёма.
6 класс. Наглядные представления о пространственных фигурах: параллелепипед, куб, призма, пирамида, конус, цилиндр, шар и сфера. Изображение пространственных фигур. Примеры развёрток многогранников, цилиндра и конуса. Создание моделей пространственных фигур (из бумаги, проволоки, пластилина и других материалов). Понятие объёма, единицы измерения объёма. Объём прямоугольного параллелепипеда, куба.
ПРЕДМЕТНЫЕ РЕЗУЛЬТАТЫ
К концу 5 класса
Распознавать параллелепипед, куб, использовать терминологию: вершина, ребро, грань, измерения, находить измерения параллелепипеда, куба.
Вычислять объём куба, параллелепипеда по заданным измерениям, пользоваться единицами измерения объёма.
Решать несложные задачи на измерение геометрических величин в практических ситуациях.
К концу 6 класса
Распознавать на моделях и изображениях пирамиду, конус, цилиндр, использовать терминологию: вершина, ребро, грань, основание, развёртка.
Изображать на клетчатой бумаге прямоугольный параллелепипед.
Вычислять объём прямоугольного параллелепипеда, куба, пользоваться основными единицами измерения объёма;
Решать несложные задачи на нахождение геометрических величин в практических ситуациях.
-
Практические работы
5 класс
Практическая работа № 1
Тема «Многогранники. Изображение многогранников. Модели пространственных тел»
Тип урока. Изучение нового материала.
Материалы к уроку: модели многогранников (параллелепипед, куб, тетраэдр, октаэдр).
-
Подсчитайте количества вершин, ребер и граней у простейших тел – параллелепипеда, куба, тетраэдра и октаэдра. Внесите в таблицу данные.
-
Примените формулу Эйлера для данных многогранников.
| Многогранник | Г | Р | В | Формула Эйлера В+Г=2+Р |
| Параллелепипед |
|
|
|
|
| Куб |
|
|
|
|
| Тетраэдр |
|
|
|
|
| Октаэдр |
|
|
|
|
-
Ответьте на вопросы:
- Что можете сказать о количествах граней, вершин и ребер параллелепипеда и куба?
- Как вы думаете, формула Эйлера выполняется для всех многогранников?
Практическая работа № 2
Тема «Объём куба, прямоугольного параллелепипеда»
Тип урока. Закрепление пройденного материала.
Материалы к уроку: модели параллелепипеда (заранее детям можно дать домашнее задание – принести коробку, имеющую форму прямоугольного параллелепипеда), карандаш, линейка, ручка.
-
Измерьте ширину, длину и высоту прямоугольного параллелепипеда и занесите в таблицу.
| Ширина, мм | Длина, мм | Высота, мм | V=? | Рисунок |
|
|
|
|
|
|
-
Вычислите объем прямоугольного параллелепипеда.
-
Изобразите прямоугольный параллелепипед.
Практическая работа № 3
«Прямоугольный параллелепипед»
(выполняется на клетчатой бумаге)
Рассмотрите рисунок и выполните задания:
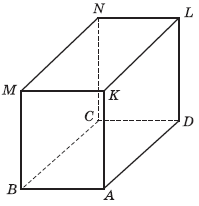
1. Выпишите все невидимые грани параллелепипеда.
2. Известны длины ребер: АВ = 3 см, АD = 6 см, AK = 4 см. Запишите длины ребер MN, NL, DL.
3. Начертите грань АВМK в натуральную величину.
Практическая работа № 4
«Многогранники»
Материал к уроку: пластилин, нож для пластилина, карандаш, ручка, линейка.
-
Слепите из пластилина куб. Разрежьте его на две части, выбирая разные направления Нарисуйте куб и покажите для каждого случая, как проходит по кубу линия разреза.
-
Какие многогранники могут получиться при разрезании куба плоскостью?
Практическая работа №5
Тема "Развёртка куба"
Материал к уроку: пластилин, зубочистки, карандаш, ручка, линейка, бумага А4, ножницы, клей.
-
Из пластилина и зубочисток составь куб.
-
Измерь ребра куба.
-
Изобрази развертку своего куба на бумаге, вырежи и склей из нее куб.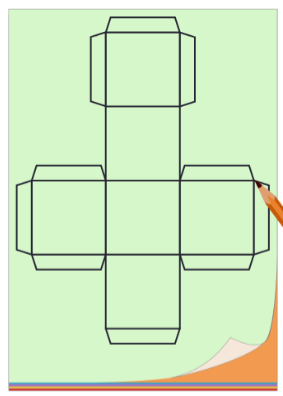
Практическая работа №6
Тема «Объём прямоугольного параллелепипеда»
Материал к уроку: 2 емкости прямоугольной формы, вода.
-
Влейте в одну емкость воду.
-
Перелейте из данной емкости воду в другую емкость.
-
Какой вывод сделаете по отношению к объемам емкостей?
-
Вычислите объём первой и второй емкостей.
6 класс
Практическая работа №1
Тема «Изображение пространственных фигур. Призма»
Материалы к уроку: модель призмы, линейка, карандаш, ручка.
-
Изобразите данную модель призмы.
-
Обозначьте вершины призмы.
-
Заполните таблицу.
| Рисунок | Названия | Обозначение на чертеже |
|
| Основания |
|
| Боковые грани |
|
| Боковая поверхность |
|
| Полная поверхность |
|
| Боковые ребра |
|
| Высота |
|
| Диагональ |
|
Практическая работа №2
Тема «Изображение пространственных фигур. Пирамида»
Материалы к уроку: модель пирамиды, линейка, карандаш, ручка
-
Изобразите данную модель пирамиды.
-
Обозначьте вершины пирамиды.
-
Заполните таблицу.
| Рисунок | Названия | Обозначение на чертеже |
|
| Основание |
|
| Боковые грани |
|
| Боковая поверхность |
|
| Полная поверхность |
|
| Боковые ребра |
|
| Ребра основания |
|
| Высота |
|
Практическая работа №1. Параллелепипед
Работа 1. Изобразите в тетради данный параллелепипед. И выполните следующие задания:
А) Назовите все вершины параллелепипеда
Б) Назовите все ребра параллелепипеда
В) Известны длины ребер: АВ = 3 см, АD = 6 см, AK = 4 см. Запишите длины ребер MN, NL, DL.
Г) Выпишите с вашего рисунка все невидимые грани параллелепипеда
Д) Вычислите площадь основания
Е) Вычислите площадь боковой поверхности
Ж) Вычислите площадь полной поверхности параллелепипеда
З) Вычислите объем параллелепипеда
Р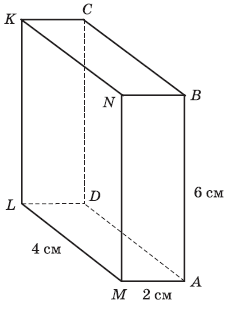 абота 2. На рисунке изображен параллелепипед и заданы его измерения. Какое утверждение является неверным?
абота 2. На рисунке изображен параллелепипед и заданы его измерения. Какое утверждение является неверным?
1) Ребра АВ и KL параллельны.
2) Расстояние от вершины А до ребра LD равно 4 см.
3) Расстояние от вершины В до грани KNML равно 6 см.
4) Диагональ параллелепипеда BL больше диагонали грани KNML.
5. Для каждого рисунка укажите соответствующее ему неравенство.
Практическая работа №2. Шестиугольная призма
Изобразите в тетради данную шестиугольную призму и выполните следующие задания:
А) Закрасьте основания призмы.
Б) Выпишите видимые боковые ребра призмы.
В) Длины ребер оснований призмы равны 10 см, боковые ребра — 15 см. Найдите длину проволоки, необходимой для изготовления каркаса призмы.
Практическая работа №3. Цилиндр
Работа 1. Мичил решил покрасить бочку без крышки изнутри. Размеры бочки составляют: высота – 80 см, диаметр основания бочки – 54 см. Сколько потребуется краски, если на 1 кв.м. расходуется 120 гр краски.
Работа 2. Выполнив необходимые измерения по данной модели цилиндра, вычислите:
А) Площадь основания
Б) Площадь боковой поверхности
В) Вычислите площадь полной поверхности цилиндра.
Практическая работа №4. Конус
Работа 1. По заданной модели конусы выполните следующие задания:
А) Измерьте длину окружности
Б) Вычислите радиус окружности
Работа 2. Изобразите заданный конус в тетради.
А) Постройте осевую симметрию конуса
Б) Отметьте произвольную точку А на боковой поверхности конуса. Постройте точку В, симметричную точке А относительно оси конуса.
Изучение геометрического материала с помощью моделей тел, дает им первые геометрические идеи, развивает у детей визуальное и наглядно-образное мышление и пространственное воображение, развивает у них конструктивные навыки.









 абота 2. На рисунке изображен параллелепипед и заданы его измерения. Какое утверждение является неверным?
абота 2. На рисунке изображен параллелепипед и заданы его измерения. Какое утверждение является неверным?




















