Министерство здравоохранения Кузбасса
Новокузнецкий филиал
Государственного бюджетного профессионального образовательного учреждения
«Кузбасский медицинский колледж»
Специальность 34.02.01
Сестринское дело
ИНДИВИДУАЛЬНЫЙ ПРОЕКТ
по дисциплине
«Математика»
по теме
«Вероятность вокруг нас»
Обучающийся _____________ Смирнова Марина Андреевна
(подпись) (ФИО)
Преподаватель _______ Шилепина Надежда Ивановна
(подпись) (ФИО)
Индивидуальный проект защищен:
«___» ____________ 20__ г.
Оценка _________________
НОВОКУЗНЕЦК 2021
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ 3
1. ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ 5
1.2. История возникновения теории вероятностей 6
1.2 Виды событий 7
1.3 Области применения теории вероятности 9
2. Практическое применение ТЕОРИЯ ВЕРОЯТНОСТЕЙ Вокруг нас 12
2.1 Анкетирование и анализ данных 12
2.2 Решение задач с помощью теории вероятности в разных областях 14
ЗАКЛЮЧЕНИЕ 17
СПИСОК ИСТОЧНИКОВ 18
Приложения 19
ВВЕДЕНИЕ
Мы живём в мире, где каждый день происходят случайные события. Многие из них остаются незамеченными, а некоторые меняют ход истории. Например, случайно изменилась погода, ученик забыл дома тетрадь или Колумб случайно открыл Америку. Люди часто используют в речи выражения «возможно», «вероятно», «будем надеяться», но вычислением появления случайного события, изучением его закономерностей занимается «Теория вероятностей».
Вероятность — одно из основных понятий не только в математической статистике, но и в жизни любого человека. Так каждому из нас каждый день приходится принимать множество решений в условиях неопределенности. Однако эту неопределенность можно «превратить» в некоторую определенность. И тогда это знание может оказать существенную помощь при принятии решения. Как ни странно, но человек часто применяет теорию вероятностей в повседневном быту, хотя может и не знать математические формулы и распределения кривой вероятности, и это не обязательно. Жизненный опыт, логика и интуиция всегда подсказывают человеку его шансы на удачу, будь то поступление на работу, карьера, личная жизнь, решение проблем, возможность выигрыша и т.п. Однако, иногда очень полезно проверить совпадает ли «эмпирический анализ» с математическим, ведь у каждого «случайного» события есть четкая вероятность его наступления.
Я выбрала данную тему проекта, потому что она интересна и познавательна. Мы часто не замечаем, что в повседневной жизни знания из разных разделов и областей математики встречаются на каждом шагу.
Актуальность: тему, выбранную мной, нельзя назвать совсем новой, но это не делает её менее актуальной, так как она связана с нашей жизнью. Я заинтересовалась, как часто мы сталкиваемся с теорией вероятностей в нашей жизни, и какую она играет роль.
Цель проекта: узнать более подробно о теории вероятностей и о возможности её применения в современной жизни.
Задачи, с помощью которых будет решаться данная цель:
-
Изучить теоретические аспекты теории вероятностей;
-
Выявить основные понятия теории вероятности;
-
Провести опрос среди студентов;
-
Показать применение теории вероятности в решении задач.
Объект исследования: теория вероятностей.
Предмет исследования: применение теории вероятностей вокруг нас.
Метод исследования: сбор, обработка теоретического материала, описание, толкование, анализ и синтез литературы, опрос студентов.
Объем и структура индивидуального проекта: композиционный состав – введение, 2 главы, заключение, 6 использованных информационных источников, 1 приложение.
Период исследования:
-
Выбор темы – октябрь;
-
Составление графика этапов – октябрь;
-
Представление итога работы – октябрь;
-
Сбор материала – октябрь-декабрь;
-
Работа над поставленными целями, задачами. Создание доклада и презентации – ноябрь-февраль;
-
Подведение итогов, формулирование выводов, оформление презентации – февраль;
-
Подготовка к выступлению с докладом – март.
- ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Математику многие любят за ее вечные истины: дважды два всегда четыре, сумма четных чисел четна, а площадь прямоугольника равна произведению его смежных сторон. В любой задаче, которую мы решаем на уроках математики, у всех получается один и тот же ответ – нужно только не делать ошибок в решении.
Реальная жизнь оказывается не такой простой и однозначной. Исходы многих явлений невозможно предсказать заранее, какой бы полной информацией мы о них не располагали. Нельзя, например, сказать наверняка, какой стороной упадет брошенная вверх монета, когда в следующем году выпадет первый снег или сколько человек в городе захотят в течение ближайшего часа позвонить по телефону.
Такие непредсказуемые явления называются случайными. Однако случай тоже имеет свои законы, которые начинают проявляться при многократном повторении случайных явлений. Именно такие закономерности изучаются в специальном разделе математики – теории вероятностей.
Теория вероятностей - математическая наука, позволяющая по вероятностям одних случайных событий находить вероятности других случайных событий, связанных каким-либо образом с первыми.
Вероятность – это числовая характеристика возможности появления случайного события в конкретных условиях, которые могут быть воссозданы многократно.
Событие – это факт, который может произойти или не произойти в результате проведения опыта или испытания.
1.2. История возникновения теории вероятностей
Теория вероятностей возникла в середине XVII в. Первые работы по ней, принадлежащие французским учёным Б. Паскалю и П. Ферма и голландскому учёному X. Гюйгенсу. Теория появилась в связи с подсчётом различных вероятностей в азартных играх. В конце XVIII – начале XIX века теория вероятности уже находит ряд весьма актуальных применений в естествознании и технике (главным образом в теории ошибок наблюдений в геодезии и астрономии, и в теории стрельбы). Развитие теории вероятности во второй половине XIX века связано в основном с именами русских математиков: П. Л. Чебышева, А. М. Ляпунова и А. А. Маркова.
Одним из основных понятий теории вероятностей является понятие события. Под событием понимают любой факт, который может произойти в результате опыта или испытания. Под опытом, или испытанием, понимается осуществление определённого комплекса условий.
Примеры событий:
-
попадание в цель при выстреле из орудия (опыт — произведение выстрела; событие — попадание в цель);
-
выпадение двух гербов при трёхкратном бросании монеты (опыт — трёхкратное бросание монеты; событие — выпадение двух гербов);
-
появление ошибки измерения в заданных пределах при измерении дальности до цели (опыт — измерение дальности; событие — ошибка измерения).
Можно привести бесчисленное множество подобных примеров. События обозначаются заглавными буквами латинского алфавита и т.д.
-
Виды событий
Различают события совместные и несовместные. События называются совместными, если наступление одного из них не исключает наступления другого. В противном случае события называются несовместными. Например, подбрасываются две игральные кости. Событие — выпадение трех очков на первой игральной кости, событие — выпадение трех очков на второй кости. И — совместные события. Пусть в магазин поступила партия обуви одного фасона и размера, но разного цвета. Событие — наудачу взятая коробка окажется с обувью черного цвета, событие — коробка окажется с обувью коричневого цвета, и — несовместные события.
Событие называется достоверным, если оно обязательно произойдет в условиях данного опыта.
Событие называется невозможным, если оно не может произойти в условиях данного опыта. Например, событие, заключающееся в том, что из партии стандартных деталей будет взята стандартная деталь, является достоверным, а нестандартная - невозможным.
Событие называется возможным, или случайным, если в результате опыта оно может появиться, но может и не появиться. Примером случайного события может служить выявление дефектов изделия при контроле партии готовой продукции, несоответствие размера обрабатываемого изделия, заданному отказ одного из звеньев автоматизированной системы управления.
События называются равновозможными, если по условиям испытания ни одно из этих событий не является объективно более возможным, чем другие. Например, пусть магазину поставляют электролампочки (причем в равных количествах) несколько заводов-изготовителей. События, состоящие в покупке лампочки любого из этих заводов, равновозможны.
Важным понятием является полная группа событий. Несколько событий в данном опыте образуют полную группу, если в результате опыта обязательно появится хотя бы одно из них. Например, в урне находится десять шаров, из них шесть шаров красных, четыре белых, причем пять шаров имеют номера. — появление красного шара при одном извлечении, — появление белого шара, — появление шара с номером. События образуют полную группу совместных событий.
Введем понятие противоположного, или дополнительного, события. Под противоположным событием понимается событие, которое обязательно должно произойти, если не наступило некоторое событие. Противоположные события несовместны и единственно возможны. Они образуют полную группу событий. Например, если партия изготовленных изделий состоит из годных и бракованных, то при извлечении одного изделия оно может оказаться либо годным — событие, либо бракованным — событие.
Формулы вычисления теории вероятности
Вероятность случайного события: 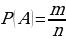 , где m – «подходящие» события; n – все возможные n исходы.
, где m – «подходящие» события; n – все возможные n исходы.
Теорема сложения вероятностей несовместных событий:
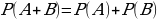
Теорема умножения вероятностей несовместных событий:
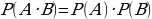
Вероятность осуществления хотя бы одного из независимых событий: 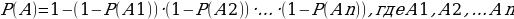 – взаимно независимые события
– взаимно независимые события
Формула Бернулли:  , где
, где 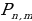 – вероятность того, что событие A наступит в n испытаниях m раз.
– вероятность того, что событие A наступит в n испытаниях m раз.
-
Области применения теории вероятности
Теперь рассмотрим области применения теории вероятности.
В физике: дело в том, что в любом опыте существует большое количество неучтенных факторов. В случае скорости света такими факторами могут быть непостоянство температуры, неточность в измерении длины волны и т. д., но они могут сказываться лишь в восьмом знаке после запятой. Степень достоверности этого утверждения и оценивается вероятностью. Теория вероятности очень важна при вычислении достоверных значений основных физических величин.
В астрономии: именно для использования в астрономии был разработан знаменитый «метод наименьших квадратов» (Лежандр 1805, Гаусс 1815). Главной задачей, для решения которой он был первоначально использован, стал расчет орбит комет, который приходилось производить по малому числу наблюдений. Ясно, что надежное определение типа орбиты (эллипс или гипербола) и точный расчет ее параметров оказывается трудным, так как орбита наблюдается лишь на небольшом участке. Метод оказался эффективным, универсальным, и вызвал бурные споры о приоритете. Его стали использовать в геодезии и картографии. Сейчас, когда искусство ручных расчетов утрачено, трудно представить, что при составлении карт мирового океана в 1880-х годах в Англии методом наименьших квадратов была численно решена система, состоящая из примерно 6000 уравнений с несколькими сотнями неизвестных.
В биологии (генетике): если пары генов g1 и g2 передаются от родителей потомку, то он получает эти гены в одной из комбинаций g1 g1, g2 g2, g1 g2 (генетически комбинации g1 g2 и g2 g1 не отличаются). С помощью деревьев можно наглядно представить наследование генов g1 и g2 (генеалогическое дерево). Пусть ген g1 передаётся с вероятностью n, а ген g2 – с вероятностью m (и от матери, и от отца), тогда 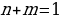 . Комбинацию g1 g1 получим с вероятностью n2, g1 g2 – с вероятностью 2nm, а g2 g2 – с вероятностью m2. Из условия
. Комбинацию g1 g1 получим с вероятностью n2, g1 g2 – с вероятностью 2nm, а g2 g2 – с вероятностью m2. Из условия 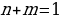 следует, что
следует, что 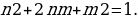
В экономике: планирование, исследование и прогнозирование экономических явлений невозможны без построения экономико-математических моделей, которые опираются на теорию вероятностей. Коммерческие банки в данный момент располагают широким охватом операций денежно-кредитного характера, но их главное направление - выдача кредитов. Сейчас у банков появляется серьезная опасность - кредитный риск. Он зависит от вероятности исполнения заемщиком всех обязательств соглашения по объемам и срокам. Величина вероятности определяется способностью заёмщика погашать кредитные обязательства.
В психологии: каждый день мы принимаем десятки решений. Они могут быть совсем мелкими и незаметными, например, перебежать дорогу на желтый свет или переждать красный и спокойно пойти на зеленый. А могут быть очень ответственными, например, в каких активах хранить сбережения. Всякий раз мы думаем, взвешиваем, пытаясь принять оптимальное решение, но как бы сильно мы ни были подготовлены, насколько бы полно не владели информацией, в наших решениях будет всегда присутствовать риск, процент удачи. Иными словами, на практике однозначно правильное решение возможно очень редко, вместо него приходится принимать вероятно более правильное, прикидочно оценивания большое количество факторов. А в таких ситуациях работает психология, вносящая коррективы в качество оценки.
В медицине: широкое применение статистических методов в медицине началось сравнительно недавно (вторая половина XX века). развитие эффективных методов лечения (антибиотики, инсулин, эффективная анестезия, искусственное кровообращение) потребовало достоверных методов оценки их эффективности. возникло новое понятие «доказательная медицина» начала развиваться более формальный, количественный подход к терапии многих заболеваний.
Таким образом, в первой главе проекта мы изучили теоретические аспекты теории вероятностей и выявили её понятия. Также рассмотрели области применения теории вероятностей. Мы встречаемся с теорией вероятностей почти каждый день, поэтому она играет значительную роль в нашей жизни, может помочь решить задачи и определить исход события.
- Практическое применение ТЕОРИЯ ВЕРОЯТНОСТЕЙ Вокруг нас
2.1 Анкетирование и анализ данных
В рамках данной темы было решено провести анкетирование. В опросе принимали участие 13 студентов первого курса. Целью данного анкетирования является определение знаний студентов о теории вероятностей.
О прос
прос
Рисунок 1
Вывод: большинство студентов знает понятие теории вероятности.
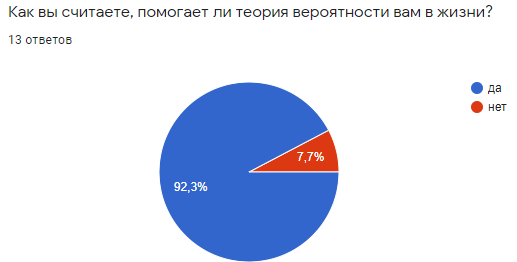
Рисунок 2
В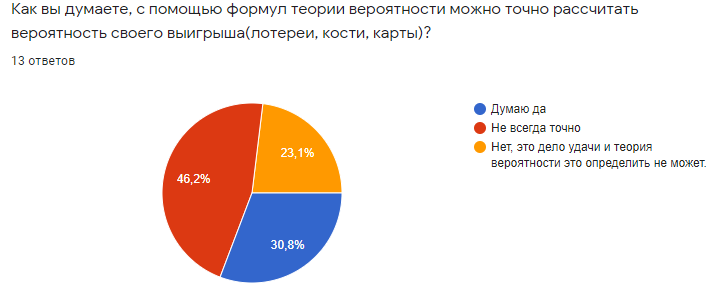 ывод: многие студенты думают, что теория вероятности помогает им в жизни, но ребят, которые думают наоборот, немало.
ывод: многие студенты думают, что теория вероятности помогает им в жизни, но ребят, которые думают наоборот, немало.
Рисунок 3
В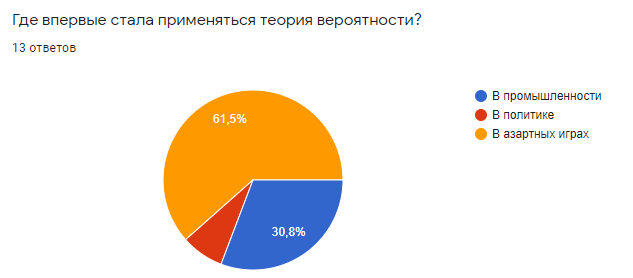 ывод: студенты проголосовали за то, что теория вероятностей помогает нам в жизни, но немало учащихся, которые думают, что теория вероятности помогает не всегда точно.
ывод: студенты проголосовали за то, что теория вероятностей помогает нам в жизни, но немало учащихся, которые думают, что теория вероятности помогает не всегда точно.
Рисунок 4
Вывод: Студенты знают, где впервые применялась теория вероятности.
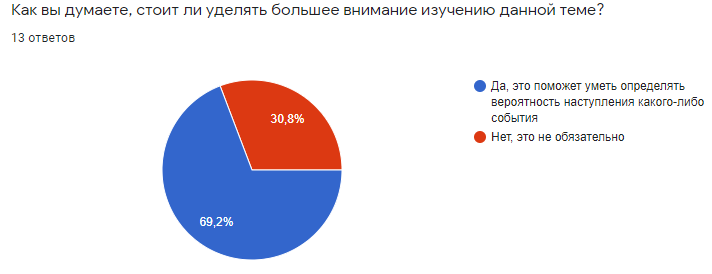
Рисунок 5
Вывод: Многие ребята проголосовали за то, что нужно уделять внимание теории вероятности.
Так как студенты проголосовали за то, что теории вероятностей поможет определять вероятность наступления какого-либо события, рассмотрим задачи с применением теории вероятностей в задачах.
-
Решение задач с помощью теории вероятности в разных областях
В медицине
Задача: однажды утром у себя на лице вы обнаруживаете красноватую сыпь и немедленно хотите узнать, не заразились ли вы корью. Врач назначает тест на корь, и его результат оказывается положительным. Больны вы или нет?
Решение: обозначим А событие «тест на корь положителен», а В – событие «у меня корь». Чтобы воспользоваться формулой Байерса, нам нужно знать вероятности Р(В), Р(А|В) и Р(А|~В). Р(В) – вероятность того, что у меня в принципе может быть корь; среди взрослых это редкая болезнь, и мы можем положить её равной 5%, т.е. Р(В)=0,05. Условная вероятность Р(А|В) описывает надёжность теста: чему равна вероятность того, что для больного человека тест даёт положительный результат? Если бы тест был совершенным, эта вероятность была бы равна 1,0 или 100%. Однако таких тестов не существует, и можно только надеяться приблизиться к идеалу. Мы оптимистически положим эту вероятность равной 0,98 (98%). Р(А|~В) – вероятность того, что тест даёт положительный результат, несмотря на то, что вы здоровы. Также было бы хорошо, чтобы это значение было равно нулю, но и эта цель недостижима. Реалистично положить вероятность «фальшивого положительного» результата равной 20% - Р(А|~В)=0,2. Теперь можно приступать к вычислениям. Мы хотим знать Р(В|А) – вероятность того, что при положительном результате действительно имеется заболевание. Воспользовавшись формулой Байерса, мы получаем результат 0,205. Вероятность того, что вы действительно больны, составляет отрадные 20%, что действительно поражает. Большинство людей ожидает, что она окажется гораздо больше. Это обусловлено тем, что, оценивая вероятность, мы недооцениваем информацию о том, что сама по себе болезнь встречается очень редко.
В Биологии
Задача: одна из форм шизофрении наследуется как рецессивный признак. Определить вероятность рождения ребенка с шизофренией от здоровых родителей, если известно, что бабушка со стороны отца и дед со стороны матери страдали этими заболеваниями.
Решение: мужчина и женщина здоровы, следовательно, они несут доминантный ген А. У каждого из них один из родителей нес рецессивный признак шизофрении (аа), следовательно, в их генотипе присутствует также рецессивный ген а, и их генотип – Аа. Вероятность рождения больного ребенка равна 1/4 (число событий, при котором появляется генотип аа, равно 1, число всех возможных событий равно 4). Вероятность рождения ребенка, больного шизофренией, равна 25% (1/4).
В сельском хозяйстве
Задача: ирландские сеттеры могут быть слепыми в результате действия рецессивного гена. Пара животных с нормальным зрением дала помёт из нескольких щенков, один из которых оказался слепым. Установить генотипы родителей. Какова вероятность рождения гетерозиготного щенка среди зрячих? (см. Приложение 1)
Решение: Аа - генотипы обоих родителей, при скрещивании получаем щенков: АА Аа Аа аа - первый - полностью зрячий (гомозиготный) второй и третий - зрячий (гетерозиготный) четвертый – слепой; соответственно вероятность рождения гетерозиготного щенка равна 2/4 или 0.5.
Итак, во второй главе проанализировали ответы на вопросы студентов. Результаты неплохие, учащиеся знают основные знания о теории вероятности. Также рассмотрели задачи, в которых можно увидеть применение теории вероятностей, приведенных выше.
ЗАКЛЮЧЕНИЕ
Теория вероятности действительно может нам помочь, ведь, подсчитав по формуле, свои шансы, мы можем понять, стоит ли делать что-то или нет. А без теории вероятности мы бы чаще ошибались, пробуя все подряд. Таким образом, зная теорию вероятности можно объяснить некоторые события нашей жизни. Благодаря теории вероятности, мы уменьшаем наши шансы на ошибку. И всегда лучше сначала узнать какова вероятность успеха, прежде чем делать.
Изучив теоретические аспекты теории вероятности, выявили её основные понятия. Также рассмотрели области применения теории вероятности и поняли, что она играет значительную роль в нашей жизни. Провели опрос среди студентов первого курса, учащиеся имеют достаточно знаний о теории вероятности. Также рассмотрели задачи, в которых можно увидеть применение теории вероятности.
Поставленная цель и задачи моей работы достигнуты.
СПИСОК ИСТОЧНИКОВ
-
Мордкович, А. Г. Математика : алгебра и начала математического анализа, геометрия. 10 класс : учебник для общеобразовательных организаций (базовый уровень) / А. Г. Мордкович, И. М. Смирнова. - 11-е изд., стереотип. – Москва : Мнемозина, 2014. - 447 с. : ил. - ISBN 978-5-346-03204-5. - Текст : непосредственный.
-
Мордкович, А. Г. Математика. 11 класс : учебник для учащихся общеобразовательных организаций (базовый уровень) / А. Г. Мордкович, И. М. Смирнова. - 11-е изд., стереотип. – Москва : Мнемозина, 2015. - 429 с. : ил. - ISBN 978-5-346-03480-3. - Текст : непосредственный.
-
Гилярова, М. Г. Математика для медицинских колледжей: учебник / М. Г. Гилярова. –. Ростов н/Д : Феникс, 2016. – 442, с.: ил. – (Среднее медицинское образование). Текст : непосредственный.
-
Теория вероятностей и основные понятия теории URL – https // bookmaker-ratings.ru/wiki/teoriya-veroyatnostej-i-osnovny-e-ponyatiya-teorii/. – (дата обращения 18.11.2020). – Текст : электронный.
-
Основные понятия и определения теории вероятностей URL – https //www.sites.google.com/site/ktnoscience/Home/lecture/l2. –(дата обращения 18.11.2020). – Текст : электронный.
-
Теория вероятностей в нашей жизни URL – https //school-science.ru/6/7/36092. – (дата обращения 18.11.2020). – Текст : электронный.
-
Приложения
Приложение 1
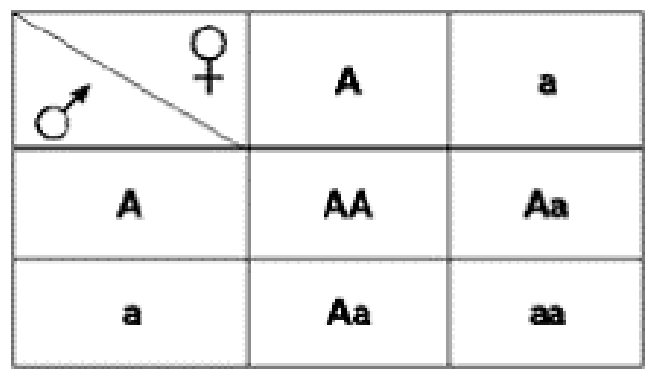
Рисунок 1 – Генотип щенков







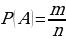 , где m – «подходящие» события; n – все возможные n исходы.
, где m – «подходящие» события; n – все возможные n исходы.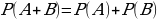
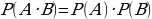
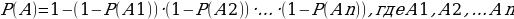 – взаимно независимые события
– взаимно независимые события , где
, где 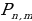 – вероятность того, что событие A наступит в n испытаниях m раз.
– вероятность того, что событие A наступит в n испытаниях m раз.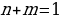 . Комбинацию g1 g1 получим с вероятностью n2, g1 g2 – с вероятностью 2nm, а g2 g2 – с вероятностью m2. Из условия
. Комбинацию g1 g1 получим с вероятностью n2, g1 g2 – с вероятностью 2nm, а g2 g2 – с вероятностью m2. Из условия 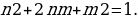
 прос
прос
 ывод: многие студенты думают, что теория вероятности помогает им в жизни, но ребят, которые думают наоборот, немало.
ывод: многие студенты думают, что теория вероятности помогает им в жизни, но ребят, которые думают наоборот, немало. ывод: студенты проголосовали за то, что теория вероятностей помогает нам в жизни, но немало учащихся, которые думают, что теория вероятности помогает не всегда точно.
ывод: студенты проголосовали за то, что теория вероятностей помогает нам в жизни, но немало учащихся, которые думают, что теория вероятности помогает не всегда точно.






















