

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 25.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Использование дидактических игр на уроках математики как одного из средств развития логического мышления младших школьников
Использование дидактических игр на уроках математики как одного из средств развития логического мышления младших школьников
Просмотр содержимого документа
«Использование дидактических игр на уроках математики как одного из средств развития логического мышления младших школьников»
Использование дидактических игр на уроках математики
как одного из средств развития логического мышления младших школьников
Учитель начальных классов
Мациева Амнат Султановна
ВВЕДЕНИЕ 3
Глава 1. Теоретические аспекты использования дидактических игр на уроках математики как одного из средств развития логического мышления младших школьников 6
1.1 Сущность логического мышления младших школьников на уроках математики и проблемы его развития 6
1.2 Психолого-педагогические предпосылки использования дидактических игр на уроках математики 18
1.3 Использование дидактических игр в практике современной начальной школы как одно из средств развития логического мышления детей 27
Выводы по главе 1 33
Глава 2. Опытно-экспериментальная работа по развитию логического мышления у младших школьников с использованием дидактических игр на уроках математики 35
2.1 Выявление уровня логического мышления младших школьников 35
2.2 Разработка системы дидактических игр на уроках математики в 1 классе 41
2.3 Результаты экспериментального исследования 54
Выводы по главе 2 57
Заключение 60
Список использованных источников 63
ПРИЛОЖЕНИЕ
ВВЕДЕНИЕ
Я.А.Коменский сказал прекрасные слова :
«Постигать вершины наук нужно без трудности ,
скуки,окриков и побоев ,а как бы играя и шутя.»
Актуальность исследования.На современном этапе развития нашего общества первоочередной задачей школы является воспитание всесторонне развитого человека. Важной составной частью этой задачи является борьба за высокое качество знаний и умений учащихся, формирование у них навыков самостоятельного умственного труда, воспитание творческой личности.
Реформа школы нацеливает на использование всех возможностей, всех ресурсов для повышения эффективности учебно-воспитательного процесса. Далеко не все педагогические ресурсы используются в сфере воспитания. К таким не часто используемым средствам обучения и воспитания относится игра.
Проблема игровой деятельности нашла свое отражение во многих педагогических теориях и системах. Значительное распространение в мировой педагогической практике приобрела созданная в первой половине ХХIвв. система дидактических игр Ф. Фребеля.
Растущий интерес к вопросам игровой деятельности в начале ХХ века реализовался во всемирно известной педагогической системе М. Монтессори, теоретическими основами которой является свободное воспитание и сенсуализм (теория, согласно которой основой психической жизни являются чувственные представления).
На развитие теории игровой деятельности в значительной мере повлияла отечественная научная педагогическая мысль. К. Ушинский отмечал, что в процессе игры «самостоятельно работает детская душа».
В конце ХІХ – начале ХХ вв. теория игровой деятельности значительно обогатилась идеями С. Русовой по организации игр разных видов.
Известные педагоги (П. Блонский, А. Макаренко, В. Сухомлинский, В. Сорока, Г. Росинский, С. Щацкий и др.) экспериментально исследовали ведущие педагогические проблемы, создали парадигмы практической воспитательной работы с учащимися в контексте различных видов игровой деятельности.
Значительное количество педагогических идей по игровой деятельности ребенка психологи высказали вскользь в результатах психологических исследований. Проблемой игры занимались такие психологи как Д.Б. Эльконин, А.Н. Леонтьев и др.
Изучение опыта работы учителей показывает, что в реальном учебном процессе для развития логического мышления детей дидактические игры используются эпизодически или вообще не используются. Многие учителя недостаточно владеют методикой использования дидактических игр на уроках в целях повышения логического мышления детей. Причиной этого, на наш взгляд, является отсутствие научно обоснованной системы использования дидактических игр, методики использования такой системы[31].
Актуальность. Недостаточная разработанность данной проблемы и объективная необходимость повышения логического мышления младших школьников обусловили выбор темы исследования.
Объект исследования – процесс развития логического мышления у младших школьников.
Предмет исследования – методическая система использования дидактических игр.
Гипотеза исследования – логическое мышление младших школьников будет развиваться активнее, если на уроках математики использовать дидактические игры в образовательном процессе.
Цель исследования – разработать и научно обосновать систему дидактических игр и методическую систему использования их на уроках математики, проверить условия эффективного их влияния на развитие логического мышления младших школьников, повышение результатов обучения.
Для реализации цели исследования необходимо было рассмотреть следующие задачи:
1. Изучить состояние исследуемой проблемы в психолого-педагогической теории; раскрыть содержание понятия «дидактическая игра».
2. Систематизировать опыт учителей по использованию дидактических игр для развития логического мышления в практике современной начальной школы.
3. Разработать систему дидактических игр на уроках математики в первом классе.
4. Проверить эффективность предложенной системы.
Для решения поставленных задач был использован комплекс методов исследования: теоретический анализ психолого-педагогической и методико-математической литературы по проблеме исследования; изучение и обобщение педагогического опыта; целенаправленные педагогические наблюдения, анкетирование, констатирующий и формирующий эксперимент.
Теоретическая значимость проведенного исследования заключается в уточнении содержания понятия «дидактическая игра», в обогащении знаний о методике использования дидактических игр для развития логического мышления, проводимых на уроках математики.
Практическое значение исследования: разработаны и проверены в ходе эксперимента система дидактических игр развития логического мышленияи методические рекомендации.
1.1 Сущность логического мышления младших школьников на уроках математики и проблемы его развития
Эффективность и качество обучения математике определяются не только глубиной и прочностью овладения школьниками системой математических знаний, умений и навыков, предусмотренных программой, но и уровнем их математического развития, степенью подготовки к самостоятельному овладению знаниями, сформированностью умений выявлять, усваивать и запоминать основное из того большого объема информации, который содержит школьный курс математики.
Таким образом, у школьников должны быть сформированы определенные качества мышления, твердые навыки рационального учебного труда, развит познавательный интерес. Поэтому естественно, что среди многих проблем совершенствования обучения математике в младшей школе большое значение имеет проблема формирования у учащихся математического мышления.
Логическое мышление - способность мыслить точно и последовательно, не допуская противоречий в своих рассуждениях, и умение разоблачать логические ошибки. Эти качества мышления имеют большое значение в любой области научной и практической деятельности. Рассуждения, в которых отсутствуют строгая логика, а вместо этого присутствуют непоследовательность и противоречие, усложняют деятельность человека[6, с.41].
Рассмотрим математическую логику.
Математическая логика на самом деле состоит из двух отдельных частей: во-первых, применением методов формальной логики в математике и математическом суждении, и, во-вторых, применением методов математики для представления и анализа формальной логики.
Специфика математики такова, что изучение этого учебного предмета, пожалуй, наиболее сильно влияет на развитие мышления школьников. В самом деле, развитие мышления школьников тесно связано с формированием приемов мышления в процессе их учебной деятельности. Эти приемы мышления (анализ, синтез, обобщение, абстрагирование и т. д.) выступают также как специфические методы научного исследования, особенно ярко проявляющиеся при обучении математике (и в частности, при решении задач).
Решение задач - вовсе не привилегия математики. Все человеческое познание есть не что иное, как непрекращающийся процесс постановки и разрешения все новых и новых задач, вопросов, проблем. И только тогда человек усвоит научные формулы и положения, когда увидит в них не просто фразы, которые предстоит запомнить, а прежде всего с трудом найденные ответы на живые вопросы, на вопросы,которые естественно вырастают из жизни.
Практика школьного обучения настойчиво требует от учителя проводить конкретную работу по развитию у учащихся математического мышления.
Математическое образование представляет собой сложный процесс, основными целевыми компонентами которого являются: а) усвоение школьниками системы математических знаний; б) овладение школьниками определенными математическими умениями и навыками; в) развитие мышления учащихся[1, с.41].
Математическое мышление является не только одним из важнейших компонентов процесса познавательной деятельности учащихся, но и таким компонентом, без целенаправленного развития которого невозможно достичь эффективных результатов в овладении школьниками системой математических знаний, умений и навыков.
Математическое мышление имеет свои специфические черты и особенности, которые обусловлены спецификой изучаемых при этом объектов, а также спецификой методов их изучения.
Прежде всего, отметим, что математическое мышление часто характеризуется проявлением так называемых математических способностей. Существует общее мнение об активной работе в процессе математического мышления определенных качеств мышления (например, гибкость, пространственное воображение, умение выделять существенное и т. д.), которые в равной степени могут быть соотнесены как к математическому мышлению, так и к мышлению физическому, техническому и т. д., т. е. к научному мышлению вообще.
К числу важных качеств научного мышления относится организованность памяти. Память каждого школьника является необходимым звеном в его познавательной деятельности, зависит от ее характера, целей, мотивов и конкретного содержания. Организованность памяти означает способность к запоминанию, долговременному сохранению, быстрому и правильному воспроизведению основной учебной информации и упорядоченного опыта.
Понятно, что в обучении математике следует развивать у школьников как оперативную, так и долговременную память, обучать их запоминанию наиболее существенных общих методов и приемов решения задач, доказательства теорем; формировать умения систематизировать свои знания и опыт[10].
Организованность памяти дает возможность соблюдать принцип экономии в мышлении. Поэтому нецелесообразно загружать память учащихся ненужной или незначительной информации, не накапливать в них опыт учебной деятельности, бесполезной для дальнейшего обучения. Так, например, до недавнего времени школьники «разучивали» решение типовых текстовых задач, не имеющих большого познавательного значения, это очень негативно сказывалось и на развитии их памяти. Опыт показывает, что организованность памяти формируется у школьников особенно эффективно, если запоминание каких-либо фактов основывается на понимании этих фактов. Поэтому зубрежка школьниками многочисленных правил является не только непродуктивной деятельностью, но и просто вредной.
В процессе обучения математике развитию и укреплению памяти школьников способствуют: а) мотивация изучения; б) составление плана учебного материала, подлежащего запоминанию; в) широкое использование в процессе запоминания, сравнения, аналогии, классификации и т. п.
Такие качества научного мышления, как ясность, точность, лаконичность речи и записи, не требуют особых комментариев.
Логическое мышление характеризуется обычно умением выводить следствия из данных предпосылок, умением вычленять отдельные случаи из некоторого общего положения, умением теоретически предсказывать конкретные результаты, обобщать полученные выводы и т. п. Известно, что развитие логического мышления школьников в процессе обучения математике является предметом особой заботы учителей и методистов. В процессе обучения математике логическое мышление проявляется (и развивается) у учащихся, прежде всего в ходе различных математических выводов: индуктивных (полная индукция) и дедуктивных, в ходе доказательств теорем, обоснований решения задачи и тому подобное[15, с.68].
Рассмотрим развитие логического мышления при обучении математике.
Об актуальности проблемы развития логического мышления школьников можно говорить в различных аспектах.
Во-первых, проблема развития логического мышления должна иметь свое отражение в школьном курсе математики в силу недостаточности подготовки учащихся в этой части, в силу большого числа логических ошибок, допускаемых учащимися при изучении школьного курса математики, где предъявляются наиболее высокие требования по сравнению с другими школьными предметами по логической организации материала.
Во-вторых, необходимо четко поставить, сформулировать проблему в силу того, что разные авторы под развитием логического мышления подразумевают разные задачи. В статьях, рекомендациях, как правило, поднимаются отдельные аспекты, общие задачи развития логического мышления. Есть необходимость в целом сформулировать проблему.
Существуют различные трактовки терминов «логика мышление», «логическое мышление». В педагогике, в методике преподавания математики эти понятия отдельными авторами понимаются очень широко как обеспечение связей в мыслях. Такое понимание охватывает и логику поиска нового знания (диалектическую логику) и логику оформления имеющегося знания и логику здравого смысла. Также имеет место смешение элементарных психологических операций процесса мышления и логических форм. Нередко к логическим операциям относят элементарные операции мышления: анализ, синтез, сравнение и др.
Задача развития логического мышления учащихся ставится и определенным образом решается в массовой школе. Во всех школьных программах по математике как одна из целей обучения предмету отмечена - развитие логического мышления. Еще век назад Л.М. Толстой отмечал, что математика имеет своей задачей не счисление, но обучение человеческой мысли при исчислении.
Но программы по математике пока что не содержат расшифровки этой цели. Поэтому каждый учитель понимает ее по-своему и по-своему ее решает. Представляется, что есть необходимость осознавать проблему развития логического мышления во всей широте и многогранности и уметь ее реализовывать в обычном учебном процессе, не привлекая дополнительного содержания, лишь расставляя в обычном учебном материале определенные акценты[3].
Выработка умений учащихся логически мыслить протекает быстрее, если обучение должным образом организовано, если осознаются отдельные логические формы. С осознанием отдельных логических форм человек начинает более четко мыслить и выражать свои мысли в языке.
По мере изучения вопросов общей и частных методик проблема развития логического мышления раскрывается более детально. Требования к формулировкам определений понятий, к построению доказательств и т. д. рассматриваются в соответствующих темах. Однако разрозненные сведения необходимо систематизировать, обобщить, углубить, довести до такого уровня, чтобы постановление целей развития логического мышления, постановка учебных задач не представляла бы трудностей.
Почему проблема развития логического мышления чаще всего поднимается в школьном курсе математики? Логично мыслить можно учить через любую науку, любой школьный предмет. Но на школьную математику в этом плане ложится наибольшая нагрузка. Ни в одном школьном предмете нет цепочек получения новых суждений, т. е. нет сложных формальных доказательств. В других школьных предметах доказательства фрагментарны, состоят из одного - двух шагов. Наличие многошаговых доказательств - одно из проявлений специфики математики - науки и школьного предмета. Отсутствие полноценного школьного курса математики существенно отражается на логическом, и, соответственно, на общем развитии человека.
Особую актуальность проблема развития логического мышления приобретает в связи с реализацией идей гуманизации школьного математического образования.
История проблемы развития логического мышления при обучении математике связана определенным образом с проблемами строгости доказательства в самой науке математике.
Логика формальных рассуждений - формальная логика дошла до нашего времени из древних времен благодаря работам древнегреческого мыслителя Аристотеля (384-322 гг. к н. э.), в которых разработана теория дедукции, т. е. правил логического вывода, независящих от содержания рассуждений. Аристотелю принадлежит открытие формального характера логического вывода, состоящий в том, что в рассуждениях одни предложения выводятся из других независимо от их содержания, в силу своей определенной структуры, формы. Отсюда и название формальной логики.
Формальная логика возникает тогда, когда развитие специальных наук и вообще человеческого мышления сделало актуальным вопрос о том, как надо рассуждать, чтобы получать правильные выводы.
В связи с появлением неевклидовой геометрии, осознанием проблемы непротиворечивости системы научных знаний возникает потребность в совершенствовании аппарата доказательств. В IXX веке в результате применения в формальной логике математических методов возникает математическая логика.
Математическая логика существенно обогатила курс формальной логики, введя большую строгость в математические доказательства на основании новых требований к получению новых суждений[22].
Основной задачей формальной логики является отделение правильных способов рассуждения от неправильных. Рассуждение можно считать верным лишь в том случае, если из истинных суждений - посылок нельзя получить ложное суждение - ложное заключение. Рассуждение, допускающее получение ложного заключения из истинных посылок, не только не расширяет наши знания об окружающем мире, но доставляет о нем неправильную информацию. Поэтому такие рассуждения недопустимы.
Анализ содержания школьного курса математики позволяет обнаружить те логические действия, которые выполняются учениками, которые изучают математический курс. Номенклатура умений может быть упорядочена следующим образом:
Учащиеся должны уметь:
- формулировать определения понятий с использованием различных связок и квантификаторов;
- приводить примеры понятий, подводить объекты под определения различных логических конструкций;
- приводить контрпримеры, т. е. строить отрицание определений различных логических конструкций;
- понимать отношения между двумя понятиями;
- проводить классификацию известных понятий;
- понимать свойства конкретных отношений - рефлективность, симметричность, транзитивность - без употребления соответствующей терминологии;
- понимать смысл терминов «следует», «следовательно», «если ..., то ... »;
- выделять условия и заключения теоремы;
- строить отрицание утверждений различной структуры;
- различать свойства и признаки понятий;
- уметь проводить полученное доказательство;
- понимать эквивалентность отдельных определений, доказывать это в отдельных случаях;
- понимать смысл терминов «хотя бы один», «не более», «не менее», «все», «некоторые».
Овладение перечисленными действиями по упорядочению изучаемого материала и является содержанием проблемы развития логического мышления.
Какие же пути решения проблемы развития логического мышления учащихся?
Для решения задач развития логического мышления не требуется включение в курс дополнительного математического материала. Задачи развития логического мышления можно ставить и решать на обычном учебном материале.
Роль математики в развитии логического мышления исключительно велика. Причина столь исключительной роли математики в том, что это наиболее теоретическая наука из всех исследуемых в школе.
В ней высокий уровень абстракции и в ней наиболее естественным способом изложения знаний является способ перехода от абстрактного к конкретному[33].
Как показывает опыт, в школьном возрасте одним из эффективных способов развития мышления является решение школьниками нестандартных логических задач.
Кроме того, решение нестандартных логических задач способно привить интерес ребенка к изучению «классической» математики. Педагогами неоднократно утверждалось, что развитие у детей логического мышления – это одна из важных задач начального обучения. Умение мыслить логически, выполнять умозаключения без наглядной опоры, сопоставлять суждение за определенными правилами – необходимо условие успешного усвоение учебного материала.
Основная работа для развития логического мышления должна вестись с задачей. Ведь в любой задаче заложены большие возможности для развития логического мышления. Нестандартные логические задачи – отличный инструмент для такого развития.
Существует значительное множество такого рода задач.
Однако, что зачастую наблюдается на практике? Ученикам предлагается задача, они знакомятся с нею и вместе с учителем анализируют условие и решают ее. Но извлекается из такой работы максимум пользы? Нет. Если дать эту задачу через день-два, то часть учеников может опять испытать затруднения при решении.
Наибольший эффект при этом может быть достигнут в результате применения различных форм работы над задачей. Это:
1. Работа над решенной задачей. Многие ученики только после повторного анализа осознают план решения задачи. Это путь к выработке твердых знаний по математике. Конечно, повторение анализа требует времени, но оно окупается.
2. Решение задач разными способами. Мало уделяется внимания решению задач разными способами в основном из-за недостатка времени. Но ведь это умение свидетельствует о достаточно высокое математическое развитие. Кроме того, привычка нахождения другого способа решения сыграет большую роль в будущем. Но я считаю, что это доступно не всем учащимся, а лишь тем, кто любит математику, имеет особые математические способности.
3. Правильно организованный способ анализа задачи - с вопроса или от данных к вопросу.
4. Представление ситуации, описанной в задачи (нарисовать «картинку»). Учитель обращает внимание детей на детали, которые нужно обязательно представить, а которые можно опустить. Мнимое участие в этой ситуации. Разбивка текста задачи на смысловые части. Моделирование ситуации с помощью чертежа, рисунка.
5. Самостоятельное составление задач учениками.
Составить задачу:
1) используя слова: больше на, столько, меньше в, на столько больше, на столько меньше;
2) решаемую в 1, 2, 3 действия;
3) по данном ее плане решения, действиям и ответу;
4) по выражению и т.д.
6. Решение задач с отсутствующими или лишними данными.
7. Изменение вопроса задачи.
8. Составление различных выражений по данным задачам и объяснение, что обозначает то или иное выражение. Выбрать те выражения, которые являются ответом на вопрос задачи.
9. Объяснение готового решения задачи.
10. Использование приема сравнения задач и их решений.
11. Запись двух решений на доске - одного верного и другого неверных.
12. Изменение условия задачи так, чтобы задача решалась другим действием/
13. Закончить решение задачи.
14. Какой вопрос и какое действие лишние в решении задачи (или, наоборот, восстановить пропущенное вопрос и действие в задаче).
15. Составление аналогичной задачи с измененными данными.
16. Решение обратных задач[2]
Систематическое использование на уроках математики и внеурочных занятий специальных задач и заданий, направленных на развитие логического мышления, организованных согласно приведенной выше схеме, расширяет математический кругозор школьников и позволяет более уверенно ориентироваться в простейших закономерностях окружающей их действительности и активнее использовать математические знания в повседневной жизни.
Важнейшей задачей математического образования является вооружение учащихся общими приемами мышления, пространственного воображения, развитие способности понимать смысл поставленной задачи, умение логично рассуждать, усвоить навыки алгоритмического мышления. Каждому важно научиться анализировать, отличать гипотезу от факта, четко выражать свои мысли, а с другой стороны - развить воображение и интуицию (пространственное представление, способность предвидеть результат и предугадать путь решения). Именно математика предоставляет благоприятные возможности для воспитания воли, трудолюбия, настойчивости в преодолении трудностей, упорства в достижении целей.
Сегодня математика как наука с многосторонними связями, что оказывает существенное влияние на развитие других наук и практики, является базой научно-технического прогресса и важным компонентом развития личности.
Одной из основных целей изучения математики является формирование и развитие мышления человека, прежде всего, абстрактного мышления, способности к абстрагированию и умения «работать» с абстрактными, «неуловимыми» объектами. В процессе изучения математики в наиболее чистом виде может быть сформировано логическое (дедуктивное) мышление, алгоритмическое мышление, много качеств мышления - такие, как сила и гибкость, конструктивность и критичность и т.д.
Поэтому в качестве одного из основных принципов новой концепции в «математике для всех» на первый план выдвинута идея приоритета развивающей функции обучения математике. В соответствии с этим принципом центром методической системы обучения математике становится не изучение основ математической науки как таковой, а познание окружающего человека мира средствами математики и, как следствие, к динамической адаптации человека к этому миру, к социализации личности.
Основной целью математического образования должно быть развитие умения математически, а выходит, логично и осознанно исследовать явления реального мира. Реализации этой цели может и должно способствовать решение на уроках математики различного рода нестандартных логических задач.
Основной целью математического образования должно быть развитие умения математически, а выходит, логично и осознанно исследовать явления реального мира. Реализации этой цели может и должно способствовать решение на уроках математики различного рода нестандартных логических задач[19].
Специфика предмета математики состоит в том, что материал каждого урока логически связан с ранее изученным, иногда значительно удаленных во времени друг от друга. На уроках математики в профессиональных учебных заведениях целенаправленное повторение материала помогает привести в систему знания учащихся, делает их более прочными и осознанными. Благодаря тому, что знания обобщаются и систематизируются, удается значительно расширить зону их применения, увеличить количество упражнений и повысить эффективность практической работы учащихся и развития логического мышления. А развитое логическое мышление учеников поможет им решать разные жизненные ситуации и профессиональные задачи,обеспечит будущему работнику возможности для самостоятельного углубленного изучения теоретических вопросов, связанных с освоением новой техники и технологии. В практической деятельности современного работника наряду с повышением требований к быстрого и точного выполнения производственных задач все большее значение приобретают элементы умственного труда. Развитие логического мышления на уроках математики будет способствовать формированию у учащихся этих способностей.
Школа – один из существующих факторов ускоренного социально – экономического развития общества. В наше время школа ищет наиболее результативные методы обучения и воспитания. Особенно эта проблема стоит перед начальным звеном школы.
Современный школьный курс математики имеет большие развивающие возможности благодаря своей целостности и логической строгости. Для того, чтобы учащиеся начальных классов усвоили важные математические идеи, положенные в его основу (множество, отношение, функция, уравнение, неравенство, геометрическая фигура и т. п), нужно подобрать такие методы и формы обучения, чтобы материал подавался на доступном для них уровне. К таким методам относят игру.
Игра относится к традиционным и интересным методам обучения и воспитания школьников. Ценность этого метода заключается в том, что в игровой деятельности образовательная, развивающая и воспитательная функции действуют в тесной взаимосвязи. Игра, как метод обучения организует, развивает учащихся, расширяет их возможности, воспитывает личность.
Игра благоприятно действует на развитие психических процессов, новых видов умственной деятельности, усвоение новых знаний и умений младших школьников, потому что в игре поэтапная отработка умственных действий происходит постоянно и ненавязчиво[18, с.52].
Важная роль игры в развитии психических процессов ребенка объясняется тем, что она вооружает ребенка доступными для него способами активного воссоздания, моделирования с помощью наружных, предметных действий такового содержания, которое при иных условиях было бы невозможным и не могло быть по-настоящему освоено.
В игровой деятельности создаются благоприятные условия для развития интеллекта ребенка, для перехода от наглядно-действенного мышления к образному и к элементам словесно-логического мышления. Именно в игре развивается способность ребенка создавать обобщенные типичные образы, мысленно преобразовывать их.
Трудно найти специалиста в области детской психологии, который не касался проблемы игры, не высказывал бы своей точки зрения на ее природу и значение, однако специальных исследований по этой проблеме очень мало, буквально единицы.
Начало изучения теории игры связано с такими именами мыслителей как Ф. Шиллер, Г. Спенсер, В. Вундт. Разрабатывая свои философские, психологические и главным образом эстетические взгляды, они постепенно, только в некоторых положениях касались игры как одного из самых распространенных явлений детской жизни.
В эмпирической психологии при изучении игры, так как и при анализе других видов деятельности преобладал функционально-аналитический подход. Одни исследователи (К.Д. Ушинский – в России, Дж. Сэлли, К. Бюлер, В. Штерн – за рубежом) видели в игре проявления отражения или фантазии, приведенные в движение разнообразными эффективными тенденциями; другие (А.И. Сикорский – в России, Дж. Дьюи – за рубежом) связывали игру с развитием мышления.
Современная психология определяет, что игра охватывает все периоды жизни человека. Это важная форма ее жизнедеятельности, а не возрастной признак. С игрой человек не расстается всю жизнь, меняются лишь ее мотивы, формы проведения, степень проявления чувств и эмоций. Разработкой теории детских игр, выяснением роли, структуры и значение игры для воспитания и обучения детей занимались психологи Ж.Пиаже, Л.С. Выготский, А.М. Леонтьев, Д.Б. Эльконин и др.
Использование игр в обучении делает неуместной авторитарную позицию учителя в общении с детьми. Ведь, чтобы заинтересовать детей предстоящей деятельностью, внести в обучение ситуации неожиданности, свободного выбора, яркие положительные эмоции, педагог должен сам стать участником игры.
Особенно важно сочетание игры с учебной деятельностью в начальных классах, когда сложный переход от дошкольного детства к школе обуславливает постепенную смену ведущих видов деятельности – игровой на учебную.
Структура развернутой игровой деятельности включает такие компоненты:
- побудительный – потребности, мотивы, интересы, стремления, которые определяют желание ребенка участвовать в игре;
- ориентировочный – выбор средств и способов игровой деятельности;
- исполнительский – операции, которые дают возможность реализовать игровую цель;
- контрольно-оценочный – коррекция и стимулирование активности игровой деятельности.
В детских играх свободная игровая деятельность выступает как самоцель. В дидактических играх, созданных педагогикой (в том числе и народной), игровая деятельность специально планируется и приспосабливается для учебных целей. Дидактические игры – разновидность игр с правилами. В мировой педагогике известны системы дидактических игр, впервые разработанные для дошкольного воспитания Ф. Фребель и М. Монтессори, для начального обучения – А. Декроли.
Дидактические игры, которые используются в начальной школе, выполняют различные функции: активизируют интерес и внимание детей, развивают познавательные способности, сообразительность, воображение, закрепляют знания, умения и навыки, тренируют сенсорные умения, навыки и тому подобное. Правильно построенная интересная дидактическая игра обогащает процесс мышления индивидуальными чувствами, развивает саморегуляцию, тренирует волевые качества ребенка.
По мнению Д.Б. Эльконина, на грани дошкольного и школьного возраста игра является основным видом деятельности в жизни ученика [15]. С психологической точки зрения, этот возраст характеризуется высокой активностью, которая ищет формы и пути реализации. В конце концов, оказывается, что именно игра остается ведущей формой жизнедеятельности детей этого возраста, компенсируя недостатки и ограниченности реальной жизни.
Игра, как отмечается в психологическом словаре, – это произвольная деятельность, отражающая в специфической условно-обобщенной форме отношение человека к миру, людям, к самой себе и имеющая целью самовыражение индивида, формирование у него определенных типов социального поведения и активизацию биологических и интеллектуальных возможностей личности [24]. Содержание понятия игры очень широкое. Существуют игры для детей и взрослых; игры сюжетно-ролевые, психологические, спортивные, азартные, деловые, дидактические и другие. В контексте нашего исследования мы, разумеется, рассмотрим лишь дидактические игры. Само их название говорит о том, что эти игры направлены на обучение. Дидактические игры являются одним из средств овладения знаниями, умениями, навыками. Нас интересуют дидактические игры, используемые на уроках математики в начальных классах.
Мнения о значение игры для развития личности можно найти в трудах выдающихся философов, педагогов и психологов.
В своем исследовании А.Н. Леонтьев пришел к выводу, что в процессе деятельности ребенка возникает противоречие между бурным развитием потребности взаимодействовать с предметами, с одной стороны, и способами реализации этого взаимодействия – с другой. Ребенок стремится к определенным действиям, но при этом не обладает теми операциями, которые нужно осуществлять в соответствии с реальными предметными условиями реализации этих действий. Это противоречие может быть устранено только в одном виде деятельности, а именно – в игре. Только в игровой деятельности требуемые операции могут быть заменены другими операциями, а его предметные условия - другими предметными условиями, причем содержание самого действия сохраняется [17].
По утверждению некоторых ученых, игра является ведущей деятельностью в младшем школьном возрасте, благодаря которой в психике ребенка происходят значительные изменения, формируются качества, подготавливающие переход к новому, более высокому уровню развития. В игровой деятельности развиваются и перестраиваются познавательные психические интересы, зарождаются новые виды деятельности, появляются элементы обучения.
Л.С. Выготский считает, что использование игровых методов в начальной школе соответствует естественным особенностям детей этого возраста, а, следовательно, способствует эффективности обучения. Такой же точки зрения придерживается и Д.Б. Эльконин. Он указывает на то, что благодаря использованию форм деятельности, которые сочетают в себе обучающие и игровые элементы, можно существенно повысить эффективность процесса обучения младших школьников [31].
Ученые единодушны, утверждая, что ученики начальной школы не имеют естественной мотивации к изучению любого учебного предмета. Игра вполне реально может выступать неким катализатором, толчком к учебе, ведь без мотива не может происходить ни один вид деятельности.
С началом обучения в школе резко меняется социальная среда ребенка, что, безусловно, влияет на ее психологическое состояние. Игра как привычная деятельность в этом возрасте помогает ей преодолеть скованность, застенчивость и страх. Поэтому, по мнению ученых, именно игровые формы обучения наиболее способствуют адаптации ребенка к новым условиям и социализации младшего школьника в школьную среду.
Игровая деятельность, в отличие от других форм работы с учениками начальной школы, создает все необходимые предпосылки для эффективной организации учебного процесса по всем предметам школьного цикла, в том числе и математики.
Подавляющее большинство ученых отмечают, что именно в игровой деятельности формируются и совершенствуются восприятие, внимание, мышление, память – фундаментальные психические процессы, без достаточного развития которых нельзя говорить о воспитании гармоничной личности.
На значение игры обращали внимание выдающиеся классики педагогики Н.К. Крупская, А.С. Макаренко.
Н.К. Крупская, изучая психологические особенности детей, отмечала, что игра является потребностью развивающегося организма. Она говорила о большие воспитательные и развивающие возможности игры: «В игре развиваются физические силы ребенка, тверже становится рука, развивается воображение, изобретательность, инициативность».
А.С. Макаренко писал: «В детском возрасте игра – это норма и ребенок должен всегда играть, даже тогда, когда выполняет серьезное дело...» Выдающийся педагог высказывался за широкое использование игры в воспитании школьников. Игра, по мнению А.С. Макаренко, – многофункциональное средство воспитательной работы. Она дает возможность воспитывать коллективизм, творческую направленность личности, сознательную дисциплину, организованность, развивает интеллектуальные способности, эстетические чувства. Особое место принадлежит игре в подготовке подрастающего поколения к труду. Хотя игра не создает материальных, культурных, иначе говоря, общественных ценностей, однако она приучает человека к физическим и психическим усилиям, нужных для работы[21].
Ученый поставил вопрос о специфике педагогического руководства игрой, где педагог должен уметь так же играть, как дети, – только тогда педагогическое руководство игрой будет эффективным. Это означает, что надо научно обеспечить профессиональную подготовку учителя к руководству игрой с учетом своеобразия этой деятельности.
Игровая деятельность как педагогическая проблема четко очерчена в научном наследии А. Запорожца. Ученый подчеркивал, что проблема игры в педагогике приобретает особую актуальность, поскольку в процессе игровой деятельности создаются особенно благоприятные условия для усвоения детьми новых знаний и умений, для формирования у них таких важных качеств человеческого ума, как способность выполнять действия в умственном плане, символически изменять реальные объекты и оперировать подобной заменой с познавательной целью.
Анализ педагогического наследия В. Сухомлинского показывает, что в глазах педагога-гуманиста игра – насущная потребность младшего школьника. Для ребенка игра является самым серьезным делом. В игре раскрывается перед детьми мир, творческие возможности личности. Без игры нет и не может быть полноценного умственного развития. Игра – это огромное светлое окно, через которое в духовный мир ребенка вливается животворный поток представлений, понятий об окружающем мире. Выдающийся педагог считал игру долей яркой духовной жизни.
Развитие ребенка в процессе игровой деятельности должно быть педагогически управляемым. Система методов и форм воспитательных воздействий в процессе игры должна строиться на учете исторического развития игры и психологического анализа – только там можно построить адекватную картину игровой деятельности, раскрыть ее закономерности и на этой основе разработать соответствующие методы педагогического воздействия на игру[11].
Игра, как известно, является самой естественной и привлекательной деятельностью для младших школьников. Еще К.Д. Ушинский писал: «Сделать серьезное занятие для детей занимательным – вот задача первоначального обучения. Каждый здоровый ребенок требует деятельности, и к тому же серьезной деятельности... С первых же уроков приучайте ребенка полюбить свои обязанности и находить удовольствие в их исполнении» [29].
Именно в играх начинается непринужденное общение ребенка с коллективом класса, взаимопонимание между учителем и учеником. В процессе игры у детей вырабатывается привычка сосредотачиваться, работать вдумчиво, самостоятельно, развивается внимание, память, жажда знаний. Удовлетворяя свою естественную неусыпную потребность в деятельности, в процессе игры ребенок «достраивает» в уме все, что недоступно ей в окружающей деятельности, в восторге не замечает, что учится – познает новое, запоминает, ориентируется в различных ситуациях, углубляет приобретенный ранее опыт, сравнивает запас представлений, понятий, развивает фантазию.
В игре наиболее полно проявляются индивидуальные особенности, интеллектуальные возможности, склонности, способности детей.
Эффективное преподавание математики в начальных классах невозможно без поисков новых путей активизации познавательной деятельности учащихся. Учащиеся должны не только усвоить определенную программой систему знаний по математике, но и научиться наблюдать объекты, явления, процессы, сравнивать их, выявлять взаимосвязь между математическими понятиями, действиями, величинами и их отношениями, научиться формировать свои выводы, пользоваться математическим языком[33].
Полученные учениками прочные знания превращаются в убеждения только тогда, когда они являются результатом сознательной самостоятельной работы мысли. Следовательно, учителю важно усваивать такие методические приемы, которые бы возбуждали мнению школьников, подводили их к самостоятельным поискам, выводов и обобщений. Современная школа должна вооружить учащихся не только знаниями, умениями и навыками, но и методами творческой мыслительной и практической деятельности.
Вполне естественно, что именно в игре следует искать скрытые возможности для успешного усвоения учащимися математических идей, понятий, формирование необходимых умений и навыков. Дидактические игры позволяют индивидуализировать работу на уроке, давать задания, посильные каждому ученику, максимально развивать их способности. Игра воспитывает чувство ответственности, коллективизма.
Играя, дети будут учиться считать, решать задачи, конструировать, сравнивать, обобщать, классифицировать, делать самостоятельные выводы, обосновывать их.
Если сначала ученик заинтересовывается игрой, то очень быстро его уже будет интересовать связанный с ней материал, в нем возникнет потребность изучить, понять, запомнить этот материал, то есть он начнет готовиться к участию в игре. Игра дает возможность легко привлечь внимание и длительное время поддерживать у учеников интерес к тем важным и сложным предметам, свойствам и явлениям, на которых в обычных условиях сосредоточить внимание не всегда удается. Например, однообразное решение примеров утомляет детей, возникает безразличие к учебе. Однако решение этих самых примеров во время игры «Кто быстрее?» становится для детей увлекательной, интересной деятельностью через конкретность поставленной цели – у каждого возникает желание победить, не отстать от товарищей, не подвести их, показать всему классу, что он умеет, знает.
Подводя итог, можно сказать, что игра – это один из важнейших методов в обучении и воспитании школьников. Рассматривая значение игры с точки зрения психологии и педагогики, утверждаем, что игра относится к средствам повышения эффективности учебно-воспитательного процесса.
Таким образом, учитывая указанные факторы, можно утверждать, что качественное развитие основных психических процессов (восприятия, внимания, памяти, мышления, воображения) в младшем школьном возрасте зависит от того, насколько успешно организована учебная деятельность. Повысить ее эффективность можно при условии использования на уроках, в частности, математики, различных видов дидактических игр, поскольку учебно-игровая деятельность, с одной стороны, способствует повышению эффективности обучения учащихся начальной школы, а с другой – создает условия для развития и совершенствования психических процессов в младшем школьном возрасте.
Не менее как три века человек пытается раскрыть тайну игры – привлекательной для ребенка деятельности, надежной помощницы педагога, бесконечно сложного явления для ученого.
Становление теории детской игровой деятельности прошло долгий и сложный путь развития.
На современном этапе развития нашего общества первоочередной задачей школы является воспитание всесторонне развитого человека. Важной составной частью этой задачи является борьба за высокое качество знаний и умений, формирование у них навыков самостоятельного умственного труда, воспитание творческой личности. Роль начальной школы в решении этой задачи решающая.
Рассмотрев монографии, статьи журналов «Начальная школа», «Начальная школа» можно сказать, что использование дидактических игр в практике современной начальной школы играет важное значение.
Вопрос включение элементов игры в учебный процесс интересует каждого, но по-разному. Одни учителя считают, что проведение занятий с элементами игры являются нецелесообразными, поскольку они не дают определенной степени решить основные образовательные задачи; другие, напротив, одобрительно относятся к проведению занятий с элементами игры, уверяют, что растет активизация познавательной деятельности учащихся. Игра – это серьезное дело, но в то же время радостная, интересная. По словам А.С. Макаренко, хорошая игра должна быть похожа на хорошую работу.
В статье Павла Копосова «Место учебной игры в методической системе современной дидактики» внимание обращается на неоднозначное и не простое решение вопроса внедрения игровой методики в учебный процесс. По мнению автора статьи, в совершенстве разработанная игровая методика может играть роль «двигателя» познавательного процесса, но совершенство «ходовой части» обеспечивает уровень эффективности методики того или иного предмета. Игра не может компенсировать несовершенства применения методики учебного предмета. Общепризнанно, что наряду со специфически предметными знаниями, умениями и навыками необходимо формировать у учащихся общеучебные навыки: самостоятельности, самоконтроля, анализа, синтеза, обобщения и тому подобное. Игра является лишь формой и не может компенсировать содержательной кризиса познавательного процесса – не обучение приспосабливается к игре, а игра – к содержанию учебного задания, в структуре которого необходимо предусмотреть и проблемность, и уровень самостоятельности, и элементы самоконтроля и тому подобное. Учебная игра несет в себе значительный потенциал активизации учебно-познавательной деятельности, необходимо лишь как в теории, так и на практике глубже раскрыть механизм взаимодействия учебного и игрового компонентов познавательного процесса.
В статье «Формирование познавательной активности учащихся в процессе совместной игровой деятельности» Елены Жорник речь идет об изменении технологий обучения в результате включения в учебно-воспитательный процесс дидактических игр. Исследования, связанные с разработкой и внедрением новых технологий обучения, в основу которых положено применение игр, свидетельствуют о наличии у них значительных возможностей повышения эффективности подготовки учителей.
Елена Жорник отмечает: «Игры дают возможность внести проблемность в познавательный процесс, осуществить самоконтроль и самокорректировку познавательной деятельности. Успешное проведение игр ведет к развитию познавательной самостоятельности учащихся». [9]
Систематизировав опыт работы многих современных школ, Елена Жорник уверяет, что дидактическая игра позволяет ярко реализовать все ведущие функции обучения: образовательную, воспитательную и развивающую. Они действуют в органическом единстве. Игра стимулирует познавательный интерес. Использование игр помогает сформировать познавательную самостоятельность – качество личности, проявляющееся в готовности собственными силами осуществить целенаправленную познавательную деятельность. Игры создают определенный эмоциональный фон в ученическом коллективе, но и требуют определенного эмоционального настроя.
Дидактические игры призваны смягчить воздействие перегрузки от однообразной механической работы в процессе многократного повторения, способствуют обострению внимания на этапе осознания новых знаний, терминов, понятий, определений.
Итак, учебная игра, как указано в данной статье, несет в себе значительный потенциал активизации учебно-познавательной деятельности, необходимо лишь как в теории, так и на практике глубже раскрывать именно механизм взаимодействия учебного и игрового компонентов познавательного процесса.
В своей статье «Использование дидактических игр в обучении» Елена Жорник рассказывает о сложности использования игры в обучении. Эта сложность связана с особенностями самой игры (доплановое поведение, отсутствие персональной ответственности каждого за результаты действий, упрощенное представление о реальности), что требует от ученика усилий для вхождения в игру. Нужно, чтобы учащиеся были сориентированы на результаты игры. Автор статьи уверяет, что игра начинается не тогда, когда ученики получают задания, а когда им становится интересно играть. Это означает, что игра вызывает приятные эмоции и дает работу уму. В статье выделены также виды эмоционального и интеллектуального стимулирования. Елена Жорник подчеркивает, что организация и проведение игр требуют большого мастерства. Педагогу нужно выбрать четкую стратегию руководства групповым общением. В дидактических играх учащиеся наблюдают, сравнивают, классифицируют предметы по признакам, выполняют анализ и синтез, делают обобщения. Активность учащихся – главный критерий эффективного проведения игры[9].
Статья Т.И. Рудаковой «Дидактическая игра – действенное средство активизации познавательной активности учащихся» раскрывает нам такие важные вопросы как:
1. Почему важна и необходима игра в начальной школе?
2. Теоретические положения об игре.
3. Дидактическая игра – действенное средство активизации мыслительной деятельности учащихся.
4. Игра – большое пространство в дальнейшей работе для педагогических наблюдений и размышлений.
В своей работе Т.И. Рудакова использует дидактические игры на уроках математики. Автор делится опытом использования некоторых видов дидактических игр при изучении определенных тем. Например, когда она ставит цель упражнять детей в прямом и обратном счете, а также закрепить знания о смежных числах, то обращается к игре «Кто знает, пусть считает дальше».Дети становятся в круг. Ведущий называет число и бросает мяч одному. Ученик должен поймать мяч, назвать число-соседа. Перед началом игры договариваются, как считать: в прямом или обратном порядке, возвращая мяч ведущему[25].
А вот пример использования подвижной дидактической игры. Игра «Математический ручеек» помогает учителю закрепить состав числа. Двое учащихся берутся за руки, образуя ворота, и держат цифровую карточку, например, 8. Остальные дети (их тоже восемь) расходятся по классу. Затем каждый должен найти свою пару 7-1, 6-2, 5-3, 4-4. Учитель подает сигнал: «Ручей к воротам!», – и дети парами проходят через ворота. «Ворота» пропускают только те пары, которые правильно составили заданное число из двух меньших, то есть состав числа.
Каждый учитель знает, насколько важным является усвоение учащимися различных случаев состава числа для успешного выполнения ими в будущем операций сложения и вычитания в пределах 10, на которых основываются вычисления всех последующих концентрах. Учителя также знают, насколько тяжело идет процесс запоминания состава чисел. А приведенная дидактическая игра иллюстрирует нам способ значительно облегчить этот процесс.
Т.И. Рудакова из опыта своей работы убедилась, что игра раскрывает детей лучше от диагностических тестов. Это для учителя в будущем – большой простор для наблюдений и размышлений. Ориентация на игру как способ обучения и форму организации деятельности помогли автору данной статьи сделать работу приятной, отношения с учениками – дружелюбными и доверчивыми, а обучение – интересным и увлекательным.
В статье «Роль современных дидактических игр в развитии познавательных интересов и способностей младших школьников» А.А. Козлова (учитель начальных классов) уверяет, что учителя должны обращать внимание на личность ребенка, развивать его лучшие качества. Но реализация этой задачи требует нового подхода к обучению и воспитанию детей. Обучение должно быть развивающим, направленным на формирование познавательных интересов и возможностей учащихся. В связи с этим особое значение имеют игровые формы обучения, в том числе, дидактические игры. Они дают возможность развивать у учащихся внимание, память и тому подобное. Игровые задания положительно влияют на развитие осознания, изобретательности учеников. Некоторые игры требуют не только умственных, но и волевых усилий: организованности, выдержки, умения соблюдать правила игры. Учительница приводит примеры дидактических игр на уроках математики, разработанные ею. При составлении дидактических игр она руководствовалась не только необходимостью повысить познавательную активность и интерес учащихся, но и желанием сформировать адекватные взаимоотношения в коллективе[13].
В статье «Формирование вычислительных навыков в процессе игры» речь идет о том, как с помощью игры можно сформировать у школьников вычислительные навыки. Как отмечается в данной статье, основная задача начального курса математики – формирование у учащихся особых, доведенных до автоматизма навыков сложения и вычитания в пределах 20 и табличных навыков умножения и деления. Автоматизм навыков достигается в процессе упражнений. Но выполнение однотипных упражнений утомляет детей. Поэтому в урок математики учителя включают игры и игровые упражнения. Среди них «Молчанка», «Угадай пример», «Круговые примеры», «Математическая эстафета» и другие.
В статье «Дидактические игры» С.А. Денис – учительница начальных классов делится с нами своим опытом работы в школе. Она уверяет, чтобы раскрыть все «секреты» школьной жизни и обучения, дать шестилеткам знания, умения и навыки, предусмотренные программой, нужно применять не только занятия, но и дидактические игры. Это одно из средств развития познавательной деятельности маленьких школьников. В данной статье учительница приводит примеры нескольких игр. Например, игру «Путешествие в лес» учитель применяет на уроке математики. Для проведения этой игры она заготовляет раздаточные карточки, силуэтные рисунки (мухомор, боровик, елка). Ученики получают по 1-2 карточки с вариантами задания под названием «Составь примеры». Ребенок сигнализирует «елочкой», примеры составлены. В награду получает «боровичок», неправильный ответ – «мухомор»[8].
Учитель-методист Неля Скопич в своей статье «Творческие упражнения и игры, как неотъемлемая часть логического мышления младших школьников» сообщает нам о том, что у учащихся шестилетнего возраста преобладают игровые интересы, произвольное поведение, наглядно-образное мышление. Это касается, в том числе и уроков математики. Неля Скопич уверяет, что увлекшись игрой, ребенок не замечает, что учится, запоминает новое, ориентируется в необычных ситуациях; пополняемый запас ее понятий, представлений, развивается фантазия. Поэтому игровые элементы дают возможность учителю заинтересовать учащихся и в течение достаточно длительного времени поддерживать их интерес к сложным вопросам, свойств и явлений, на которых в обычных условиях сосредоточить внимание детей не всегда удается.
В монографии Н.И. Никитинской, Н.Д. Мацко рассматриваются вопросы организации и управления игровой деятельностью младших школьников в процессе усвоения важных математических понятий. Особое внимание уделено проблемам развития творческих возможностей учащихся, их памяти, внимания, представления. В данной монографии описывается дидактическая и воспитательная цель игр, даются методические рекомендации по проведению игр на различных этапах урока.
М.В. Богданович в своей монографии «Методика преподавания математики в начальных классах» тоже вспоминает о дидактические игры. Он считает, что на уроке игра организуется не для того, чтобы дети поиграли, а, чтобы чему-то научились. Автор данной монографии уверяет, что игра не предшествует выполнению учебных заданий и не чередуется с ними, а является одной из форм организации коллективной работы учащихся в классе.
Выводы по главе 1Проведенное теоретическое исследовании, посвященное проблеме использования дидактических игр на уроках математики в начальной школе с целью развития логического мышления детей, позволило решить поставленные задачи и сформулировать основные результаты исследования.
1. Изучая состояние исследуемой проблемы в педагогической теории и практике, мы пришли к следующим выводам.
• Потребность современного общества требует от школы наиболее результативных методов обучения и воспитания, и эта потребность стоит перед начальным звеном школы.
• Проведен анализ научных разработок, учебной и методической литературы, работы учителей начальных классов показывает, что и в теории, и в практике школы проблема использования дидактических игр имеет определенное отражение. Однако на сегодня нет целостного подхода к решению этой проблемы: отсутствует научно обоснованная система дидактических игр и методика их использования в начальной школе.
2. Дидактические игры на уроках математики не полностью используются учителями не за то, что не имеет методических указаний и образцов их проведения, а из-за того, что некоторые учителя не хотят их проводить по определенным причинам. Об этом грустно узнавать, ведь работа такого учителя уже не имеет нужной эффективности, не заинтересовывает детей, а наоборот отбивает у них желание учиться. Конечно, такое обучение не приведет к полному всестороннему развитию личности.
3. Следовательно, каждый учитель начальных классов должен осознать, что, используя дидактические игры на уроках математики улучшает учебный процесс учащихся. В игре ребенок развивается, познает что-то новое, лучше усваивает материал урока и тому подобное.
2.1. Выявление уровня логического мышления младших школьников
Результативность проведенного исследования изучалась путем постоянных наблюдений, анкетирования, которые проводились как в процессе констатирующего эксперимента, так и формирующего. Исследования проводились на базе четырехлетней начальной школы. Рассмотрим отдельно результаты констатирующего и формирующего экспериментов.
Основной задачей констатирующего эксперимента было определение уровня логического мышления учеников начальной школы. На основе анкетирования среди учителей ГБОУ «Лингвистическая школа им.Ю.Д.Дешериева» было выяснено, что большинство учителей начальных классов в той или иной степени используют дидактические игры на уроках математики и во внеурочное время, но основная масса учителей делает это эпизодически. Мы выяснили, что учителя испытывают трудности в подборе дидактических игр для соответствующих уроков. Все это мы описали в третьем параграфе первой главы.
В ходе эксперимента изучалась и деятельность учащихся в работе над дидактическими играми. Чтобы выяснить этот вопрос, мы провели серию наблюдений на уроках математики, причем классы нами выбирались только те, в которых учителя использовали дидактические игры более-менее систематически. Также проводились беседы с учениками.
На основе материалов констатирующего эксперимента в значительной мере были определены и вопросы отбора и содержания дидактических игр: как игр из учебника или пособия, так и тех дополнительных игр, которые учителя подбирают к уроку самостоятельно. Как правило, дидактические игры, подобранные учителями самостоятельно, копируют игры учебника или пособия. Оригинальные среди них попадаются редко. Поэтому в нашем исследовании нужно было разграничить дидактические игры учебника или пособия и дидактические игры, подобранные учителями самостоятельно и уже на основе этого разграничения строить собственную систему дидактических игр. По этим материалам была разработана экспериментальная система, которая включала 28 игр.
В ходе экспериментальной работы мы столкнулись с потребностью выяснить вопрос о формах организации работы над дидактическими играми: фронтальную, индивидуальную методику их использования. Изучая причины, через которые на многих уроках не нашлось времени для запланированных учителями игр, мы пришли к необходимости исследовать особенности использования дидактических игр на различных этапах урока и пришли к выводу, что лучше всего использовать дидактические игры на этапе устных вычислений. Было определено также, какие конкретные виды дидактических игр стоит включить в экспериментальную работу.
Эта первая часть научной работы послужила отправной точкой нашего исследования, в ходе которого эксперимент выводился на качественно иной теоретический уровень. Для этого надо было переосмыслить суть процесса обучения математике в начальной школе и место в нем дидактических игр как метода развития логического мышления ученика.
Задача формирующего эксперимента заключалась в том, чтобы обосновать и проверить ряд положений, рекомендаций и показателей.
Нужно было проверить и уточнить составленную систему дидактических игр для 1 класса; определить и уточнить методы и формы работы с дидактическими играми; определить эффективность применения разработанной системы дидактических игр и методики ее использования.
Методика формирующего эксперимента включала проведение учителем специально разработанных нами уроков и их фрагментов; непосредственное проведение занятий самим исследователем; наблюдение за действиями учителя и учащихся в процессе работы с дидактическими играми; анкетирование и анализ устных ответов учащихся; проведение бесед с учителем и учащимися о применении дидактических игр экспериментальной системы.
Вопросы методики проведения экспериментальной системой были поданы учителю в виде конспектов отдельных уроков или фрагментов уроков. Общая картина проведения эксперимента была разъяснена учителю в процессе консультаций. Во время прохождения педпрактики уроки проводились самим исследователем.
Формирующий эксперимент проводился в МБОУ СОШг В течение которых было охвачено 60 учащихся 1 А и 1 В классов.
Эксперимент состоял из трех этапов: 1) предварительного изучения уровня логического мышления учеников; 2) формирующего этапа с элементами поиска; 3) изучение результативности исследования.
Результативность исследования оценивалась на основе использования учителями дидактических игр; частично использовалось сравнение результатов начального и конечного контроля, а также бесед с учителем и непосредственных наблюдений.
Согласно целей и этапов эксперимента, мы поставили перед собой следующие задачи: 1) выявить у учителей наличный (исходный) уровень сформированности умений проводить дидактические игры на уроках математики с целью развития логического мышления; 2) параллельно с обучением учащихся математике в объеме требований учебной программы ознакомить учителей с новыми способами и формами работы над дидактическими играми с целью развития логического мышления учеников; согласно возможностей учителей и учащихся осуществить окончательный отбор содержания системы дидактических игр и уточнить методику их проведения; 3) проверить эффективность разработанной методики путем выявления нового уровня сформированности логического мышления учащихся.
В ходе первого этапа эксперимента мы провели контроль устных вычислений, который проводился как в экспериментальном, так и в контрольном классе в конце октября. Моя задача состояла в наблюдении за действиями и поступками учителей и учеников на этих уроках и на основе этого сделать соответствующий итог. Приведем содержание этих дидактических игр.
Игра «Покажи нужную цифру»
Материал игры: карточки с изображением предметов, мелкие предметы, игрушки.
Содержание игры. Учитель показывает учащимся карточку с изображением нескольких предметов, а ученики, быстро посчитав, показывают соответствующую цифру.
Игра «Будь внимательным»
Содержание игры. Учитель зачитывает стихотворение и называет его участников, а ученики посчитав показывают соответствующую числу цифру.
В класс зашел Мухаммад,
А за ним – Ахмед,
За ним – Залина,
За ней Самира,
А позади Идрис.
Сколько здесь малышей?
Результаты контроля обобщены в таблице 1.
Таблица 1Правильность ответов учащихся в устных вычислениях в начале года в экспериментальном и контрольном классе
| Классы | Количество учеников (в %) | |||
| Игра «Покажи нужную цифру» | Игра «Будь внимательным» | |||
| Правильно ответили | Неправильно ответили | Правильно ответили | Неправильно ответили | |
| 1‑А экспер. | 23 | 77 | 24 | 76 |
| 1‑В контр. | 21 | 79 | 22 | 78 |
Из таблицы видно, что результаты этого контроля примерно одинаковые и в контрольном, и в экспериментальном классе.
Ответы учащихся приведены на рис. 1 и 2.
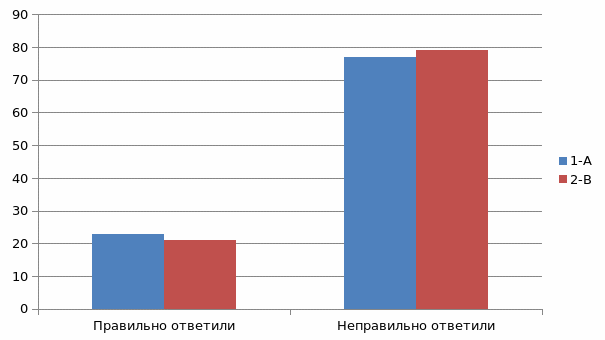
Рисунок 1 – Ответы учащихся на задания в игре «Покажи нужную цифру», количество
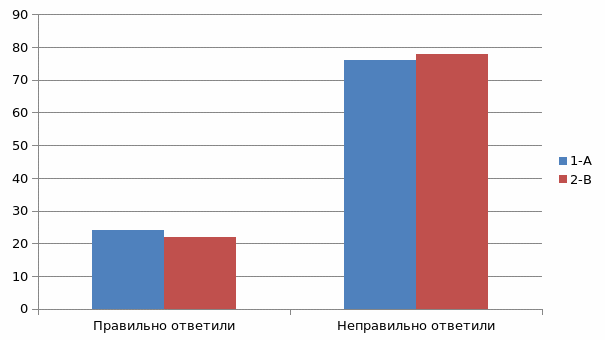
Рисунок 2 – Ответы учащихся на задания в игре «Будь внимательным», кол-во
В ходе констатирующего эксперимента были выявлены затруднения, которые вызвали у учащихся дать правильный ответ в ходе игр. Наблюдая за учениками данных классов, мы заметили, что активность их на уроке велика, однако это не означает, что каждый ученик отвечал правильно. Так, в начале эксперимента в 1 А классе дали правильный ответ 7 учеников, а в 1 только 5 учеников.
Работа учителя как экспериментального, так и контрольного класса была нацелена на то, чтобы сформировать у учащихся умение быстрого счета. Так игру «Покажи нужную цифру» они проводили в показательной форме, где показывали ученикам карточку с изображением нескольких предметов, а ученики, быстро посчитав, должны показать соответствующую цифру.
Трудности, связанные с данной игрой, оказались типичными для учеников. Им трудно было воспринимать показательную форму игры и, хотя активность их была велика, зато правильность ответов низкой.
Наблюдая за учениками, мы убедились, что они лучше восприняли игру в словесной форме, и поэтому правильность ответов несколько лучше. Однако другие игры лучше воспринимались в зрительной форме. Подобные трудности характерны для младшего школьного возраста, поэтому избавиться от них полностью невозможно. Пути постепенного преодоления их мы видим в регулярном проведении учителями разнообразных форм дидактических игр.
Заметим, что только сильные ученики класса полностью участвовали в играх.
Еще одна трудность, с которой мы столкнулись в ходе эксперимента, заключалась в том, что иногда было трудно выбрать оптимальный вариант проведения игр. Это требовало с нашей стороны более детального изучения форм и методов проведения игр. Нужно было учитывать не только соотношение сильных и средних учеников и общую подготовленность класса, но и дидактическую ситуацию на уроке.
В дальнейшем в нашем исследовании работа заключалась в том, чтобы предоставить учителю экспериментального класса разработанную нами систему дидактических игр, по которой он должен был работать в течение остального учебного года. То есть учитель должен проводить уроки математики с использованием дидактических игр нашей системы. Конечно, учитель контрольного класса тоже проводил уроки математики с использованием дидактических игр, но не из нашей системы. Он использовал игры учебника или пособия, или подбирал игры к уроку самостоятельно и делал это не так регулярно, как учитель экспериментального класса.
В ходе эксперимента сравнение эффективности обучения в экспериментальном и контрольном классе осуществлялась по следующим показателям: 1) по результатам усвоения основного материала программы по математике для начальных классов; 2) по результатам использования разработанных нами игр; 3) за изменениями в общем развитии детей, их интересах, отношении к учебе.
В конце эксперимента в экспериментальном и в контрольном классе мы снова провели контроль устных вычислений.
Разрабатывая систему дидактических игр на уроках математики в 1 классе, нужно исходить из методического анализа понятия дидактическая игра, учитывать цели использования игр на уроках математики, потребность в оптимизации учебного процесса, индивидуальные возможности младших школьников. При этом следует придерживаться следующих концептуальных требований:
1. Система должна способствовать развивающему обучению математики, оптимальному развитию каждого ребенка в частности.
2. Игры системы должны быть согласованы с тем материалом, который изучается по учебнику и находится в зоне доступности ребенка.
3. Система должна осуществлять пропедевтическую функцию в изучении математики, в частности, знакомить учащихся с различными разделами математики.
4. Система должна учитывать современные условия школьной практики, быть удобной для работы учителя.
Система дидактических игр разрабатывалась на основе анализа стабильного учебника математики, пособия для учителя, рекомендаций научного руководителя. В процессе работы оказалось, что большое количество дидактических игр целесообразно применять совместно с соответствующим программным материалом, который изучается в 1 классе. Поэтому данная система включает в себя следующие подсистемы дидактических игр:
1. Дидактические игры, связанные с изучением свойств и отношений предметов.
2. Дидактические игры, связанные с изучением нумерации чисел первого десятка и числа 0.
3. Дидактические игры, связанные с изучением практических действий в пределах 10.
4. Дидактические игры, связанные с изучением нумерации чисел второго десятка.
В каждую подсистему входят игры, разнообразные по форме их проведения, а именно: фронтальные игры, индивидуальные игры, подвижные игры, спокойные игры, игры-соревнования и тому подобное. Общий вид системы дидактических игр, которая использовалась нами в 1 классе, можно изобразить следующей структурной схемой:



Подвижные
Соревнования
Игры жестов






Эстафеты
Игры с мячом м’ячем


Дидактические игры, связанные с изучением свойств и отношений предметов
Дидактические игры, связанные с изучением нумерации чисел первого десятка и числа 0
Дидактические игры, связанные с изучением нумерации чисел второго десятка
Дидактические игры, связанные с изучением практических действий в пределах 10.





Спокойные


Фронтальные
Индивидуальныені
Рисунок 3 - Общий вид системы дидактических игр, которая использовалась нами в 1 классе
Как видно из схемы, новые виды игр в течение года вводятся постепенно и к концу первого класса дети знакомы со всеми названными видами игр.
У учащихся шестилетнего возраста преобладают игровые интересы, произвольное поведение, наглядно-образное мышление. Поэтому использование дидактических игр на уроках, в частности, математики играет важное значение. Увлекшись игрой, ребенок не замечает, что учится, запоминает новое, ориентируется в необычных ситуациях; пополняемый запас ее понятий, представлений, развивается фантазия. Игровые элементы дают возможность учителю заинтересовать учащихся и в течение достаточно длительного времени поддерживать их интерес к сложным вопросам, свойств и явлений, на которых в обычных условиях сосредоточить внимание детей не всегда удается.
Используя дидактические игры уже с первого класса на уроках математики можно заметить, что у первоклассника происходят ощутимые изменения в его мышлении: развивается умение анализировать, обобщать, делать выводы, доказывать целесообразность своих действий.
Подаем содержательную характеристику каждой подсистемы дидактических игр, которые можно использовать на уроках математики в 1 классе.
Дидактические игры, связанные с изучением свойств и отношений предметов.
Первый урок математики в первом классе начинается с изучения темы «Знакомство учащихся с учебником. Предмет. Фигура. Счет предметов». Поэтому, чтобы уточнить знания и умения учащихся называть числа от 1 до 10, считать предметы учителю следует предложить учащимся дидактическую игру во время работы со счетным материалом. Игра называется «Сколько?»
Материалы игры: карточки с цифрами, карточки с изображением разного количества предметов, игрушки, наборное полотно.
Содержание игры. Вариант 1. Учитель выставляет на наборном полотне карточки с изображением, например, звездочек и, показывая каждую из них указкой, предлагает считать хором. Потом указкой показывает звездочки, начиная с последней, а ученики хором считают от последней к первой. Учитель должен обратить внимание детей на то, что в обоих случаях получили одно и то же число. Далее, вынимая карточки со звездочками по одной (намеренно не по порядку), он предлагает детям снова считать хором. Выясняется, что и в этом случае получили то же число. Затем учитель ставит на место все карточки по одной, а дети вслух их считают. После этого учитель заменяет, например, две карточки со звездочками карточками с шарами и предлагает детям сосчитать, сколько всего карточек на напорномполотне. Когда дети получат опять то самое число, учитель предлагает карточки со звездочками заменить карточками с шариками и снова сосчитать. Оказывается, что и в этот раз количество карт такое же.
Вариант 2. Учитель выставляет игрушки на столе или на карнизе доске и предлагает ученикам, показывая игрушки указкой, не только считать вслух, но и поднимать цифру, которую они называют. Дети считают в прямом и обратном порядке, с заменых отдельных игрушек.
Вариант 3. Учитель хлопает в ладоши несколько раз, а ученики, посчитав количество аплодисментов, молча поднимают карточку с соответствующей цифрой.
Вариант 4. Учитель хлопает в ладоши, ученики также хлопают и считают аплодисменты.
Вариант 5. Учитель показывает таблицу с изображением различных или одинаковых предметов (или выставляет карточки на наборном полотне) и предлагает молча сосчитать и показать соответствующую цифру.
Наряду с выработкой умений счета значительное внимание следует уделять в этот период выяснению отношений: «больше», «меньше», «столько же». Учащиеся знакомятся с однозначным соответствием, а затем учатся определять, каких предметов больше, а каких меньше. Важно, чтобы отношения «больше» – «меньше» с самого начала выступало во взаимосвязи, чтобы дети сразу же осознавали, что, когда в одной из сравниваемых совокупностей предметов больше, то это означает, что во второй их меньше. Постепенно ученики учатся выяснять, на сколько в одной из групп предметов больше (меньше), чем во второй, что надо сделать, чтобы предметов в обеих группах стало поровну. Поэтому во время изучения темы «Сравнение групп предметов по количеству,понятий одинакового количества, неодинакового количества, столько же, больше, меньше можно использовать игру «Покажи «столько же», «больше», «меньше»».
Материалы игры: в учителя и учеников набор карточек с числами и различные предметы.
Содержание игры. Вариант 1. Учитель показывает учащимся карточку с числом 3 и говорит: «Больше», ученики показывают 4, 5 и более предметам, или карточку с изображением более 3 предметов. Когда учитель говорит: «Столько же» и показывает карточку с числом 5, все дети поднимают в руке 5 предметов, когда учитель показывает число 5 и говорит: «Меньше», ученики показывают 2-3 предмета и т. д.
Вариант 2. Учитель показывает карточку с числом и говорит: «Больше», «Меньше», «Столько же», а ученики поднимают карточки с большим, меньшим и таким же числом.
Наряду с выработкой умений счета проводится работа по уточнению таких пространственных представлений: слева – справа, выше – ниже, длиннее – короче, шире – уже, перед, после, под, над, за, посередине и т. д. и широко используются, уточняются и расширяются представления учащихся об известных им геометрических фигурах.
Чтобы лучше сформировать у учащихся вышеперечисленные пространственные представления, учителю необходимо использовать соответствующие игры. А именно, во время изучения темы «Взаимное расположение предметов в пространстве (посреди, позади, под, над, на, за). Счет предметов» можно провести игру «Назови своих соседей».
Учитель спрашивает детей, кто сидит рядом с ними за партой, кто сзади, спереди.
С помощью этой игры у детей формируются соответствующие представления. Игру нужно предлагать учащимся после изучения нового материала. Это дает возможность лучшему усвоению данного материала.
Игру «Составим узор» можно использовать на уроке во время изучения темы «Взаимное расположение предметов (сверху, снизу). Направление (вверх, вниз)»
По заданию учителя из геометрических фигур на парте в один ряд ученики составляют узор: 5 треугольников, под треугольниками – кружочки, над треугольниками – квадратами. Затем учащиеся меняют узор и рассказывают, как они разместили геометрические фигуры.
Данная игра учит учеников размещать предметы в пространстве, различать предметы за размещением, знакомит с направлениями движения: вверх, вниз, расширяются представления о геометрические фигуры, формируется навык счета.
Для лучшего уточнения таких пространственных представлений: выше – ниже, длиннее – короче можно использовать игру «Выше – ниже, длиннее – короче».
Содержание игры. Учитель предлагает всем ученикам быстро встать и, в зависимости от слов, сказанных учителем, показать ниже (выше), чем показывает он сам.
Вариант 1. Учитель показывает ниже (выше) стола и говорит «выше» («ниже»). Дети быстро поднимают руки значительно выше (ниже), чем показал учитель.
То же касается и слов «длиннее – короче». Учитель показывает ученикам определенное расстояние между ладонями своих рук и говорит «дольше» («короче»), а дети соответственно показывают большую (меньшую) расстояние, чем у учителя.
Вариант 2. Игра проводится аналогично первому варианту, но осложняется тем, что учитель показывает рукой высоту и говорит «выше», а сам опускает руку ниже. Ученик должен сделать наоборот. То же касается и «шире – уже». Эта игра, как правило, вызывает оживление, смех, поскольку ученики часто ошибаются, и является действенным средством для снятия переутомления.
Мы привели подробные описания игр этой подсистемы. Относительно индивидуальных, то они проводились нами с использованием индивидуальных карточек с изображением игры (например, «Забей гол в ворота», «Установи соответствие», «Поймай рыбку» и другие).
Дидактические игры, связанные с изучением нумерации чисел первого десятка и числа 0.
Изучая нумерацию чисел первого десятка, школьники учатся читать и записывать эти числа, сравнивая их, используя знаки«», «=», определять место каждого числа в числовом ряду, решать примеры на сложение (вычитание) единицы, например: 5 + 1, 7 + 1, 9 – 1, 3 – 1 др. А дидактическая игра «Больше, меньше, поровну» поможет учащимся лучше усвоить данный материал.
Материал игры: у каждого ученика на парте набор знаков:,
Содержание игры. Учитель вывешивает таблицу или открывает доску с заранее подготовленными записями цифр.
Ученикам каждого варианта надо на своей парте разложить предметы так, как показано в записях, и поставить нужные знаки. Проверить правильность выполненных действий можно предложить соседям по парте, или это делает учитель, быстро пройдя между партами.
На основе наблюдений и сравнения конечных множеств первоклассники делают вывод: каждое следующее число больше на 1 от данного, а каждое предыдущее меньше на единицу от данного: если добавить или вычесть 1, то соответствующее число станет больше или меньше на 1; чтобы увеличить (уменьшить) число на 1, нужно прибавить (вычесть) 1; если добавить 1, то получим следующее число, а если вычесть 1, то получим предыдущее число. Поскольку в этот период обучения детям еще трудно длительное время сосредотачиваться и управлять своим вниманием, предпочтение следует отдавать подвижным играм (аплодисментам, манипуляциям с предметами, перемещению детей, движениям руками и тому подобное).
Целью приведенных выше игр является формирование у учащихся пространственных и количественных представлений, выработка вычислительных и графических умений и навыков, а именно:
1. Свободно считать, называя числа в прямом и обратном порядке, начиная с любого числа.
2. Знать, как можно достать (создать) каждое число различными способами.
3. Знать, как называются числа и как они записываются. Умение ставить в соответствие числу цифру и наоборот.
4. Умение отыскать, какое место занимает каждое число в натуральном ряде чисел и какое число стоит перед (меньше на 1) и после (больше на 1) данного числа.
5. Знать и представлять, что каждое названное число больше всех тех, что ему предшествовали, и тем меньше всех чисел, что идут за ним.
6. Умение ориентироваться в пространстве.
В процессе работы над нумерацией чисел первого десятка учитель подготавливает учащихся к изучению действий сложения и вычитания. Чтобы сформировать правильные представления об этих действиях, наряду со случаями сложения и вычитания, на которых раскрывается принцип образования чисел натуральной последовательности, рассматриваются случаи сложения и вычитания вида: 2+2, 3+2, 5-2, 5-3, 1+4, 5-4, 4-2. К пониманию смысла действий школьники подходят на основе операций над совокупностями предметов. Действительно, объединение конечных множеств, то есть нахождению ответа на вопросы типа «сколько всего?», – соответствует действие сложения чисел, а выделение части множества, то есть нахождению ответа на вопрос типа «сколько осталось?», «сколько стало, когда отдали?» и др. соответствует действие вычитания чисел.
Выполняя операции над множествами предметов и действий над числами, ученики воспринимают и количественные отношения «больше на...», «меньше на...». Поэтому примеры на сложение и вычитание предлагаются им в форме «увеличить на…», «уменьшить на...».
Во время изучения соответствующего материала учитель может провести на уроке дидактическую игру «Увеличить и уменьшить на 1».
Материал игры: карточки с числами.
Содержание игры. Учитель поднимает вверх карточку с любым числом, а ученики поднимают в левой руке карточку с таким числом, которое получится в результате увеличения данного числа на 1, а в правой руке – карточку с числом, которое образуется при уменьшении данного числа на 1. Скажем, учитель поднимает карточку с числом 7. Ученики должны в левой руке поднести карточку с числом 6.
В игре побеждает ряд учеников, которые ни разу не ошибались или ошибались меньше.
Во время усвоения нумерации чисел в пределах 10 у учащихся формируется понятие о нуль, как число элементов пустого множества. Отнимая по одному элементу из данного множества до тех пор, пока в ней не останется ни одного элемента, ученики каждый раз называют количество элементов каждого множества.
Чтобы сформировать у детей понятия о числе и цифре 0, а также на основе практических действий с предметами раскрыть образование ноля, определить его место в натуральном ряде учителю поможет дидактическая игра «Образуй числовой ряд».
Играют две команды. У каждого ученика – карточки с цифрами. По сигналу учителя команды должны образовать числовой ряд слева направо (справа налево). Выигрывает команда, которая быстро и правильно выполнит задание.
Данная игра проводится в начале урока, чтобы подготовить детей к изучению нового материала, повторить уже изученный материал, то есть числовой ряд, размещения чисел в ряде. Далее учитель знакомит детей с числом и цифрой 0.
Сравнив нуля с другими числами натурального ряда, дети устанавливают, что ноль меньше чисел 1, 2, ..., 10, поэтому должна стоять в числовом ряду перед числом 1. На этом этапе работы учитель замечает, что ноль – начало числового ряда, начало отсчета на линейке, цифра для обозначения чисел (0, 10, 20, 30, 40...).
Дидактические игры, связанные с изучением практических действий в пределах 10.
После изучения темы «Порядковая и количественная счет» дети начинают изучать тему «Составление примеров на сложение. Знак «+» (добавить). Чтение и решение примеров на сложение». Задача учителя на данном уроке состоит в том, чтобы ознакомить детей со знаком «+» (добавить), учить учащихся составлять примеры на сложение. Уже на следующем уроке дети упражняются в усвоении результатов сложения в пределах 5 на основе состава чисел.
Для лучшего упражнения в усвоении результатов добавление учитель может предложить детям игру «Восстанови числа».
Содержание игры. Учитель говорит: «На снегу белочка засыпала примеры. Подул ветерок и часть примеров засыпал снежком. Помогите белочке восстановить числа в примерах».
... + 2 = 4 ... + 1 = 5
... + 2 = 5 ... + 1 = 4
Данная игра предлагается детям на уроке после изучения нового материала, чтобы они упражнялись в усвоении действия сложения.
Игру «Помоги зверятам» учитель может использовать на уроке как для усвоения действия сложения.
На доске – рисунки зверушек, под ними примеры.
– Белочка, зайчик и ежик на уроке математики в лесной школе решали примеры. Подкралась хитрая лиса и украла цифры. Помогите зверятам восстановить примеры.
Класс разделен на три команды.
Одна команда помогает белочке, вторая – зайчик, а третья – ежику. Побеждает команда, которая правильно выполнила задание.
| 5 | 4 | + |
| + | + | 4 |
| 6 | 3 | 2 |
В 1 классе дети не только решают примеры на сложение, а и еще на вычитание, то есть знакомятся с действием вычитания, знаком «–» (вычесть). Во время изучения данной темы, учитель на основе рассмотрения рисунков и практических действий с предметами раскрывает смысл действия вычитания, взаимосвязь действий сложения и вычитания. Учит учащихся составлять, читать и решать примеры на вычитание по рисункам.
Для усвоения таблиц сложения и вычитания в пределах 10 учитель может предложить ученикам следующие игры: «Молчанка», «Эстафета», «День и ночь».
Данные игры предлагаются на этапе устных вычислений.
Игра «День и ночь».
Учитель задает ученикам вопросы, а ученики должны быстро отвечать на них.
- Число 7 уменьшить на 5.
- Первое слагаемое 2, второе слагаемое 6. Найти сумму.
- На сколько число 9 больше числа 5?
- На сколько число 7 меньше числа 10?
Игра «Эстафета».
Ученики по очереди называют примеры из таблицы сложения числа 4; таблицы вычитания числа 5. Выигрывает тот ряд, в котором все ученики быстро и правильно назовут соответствующие примеры.
Игра «Молчанка».
Учитель молча показывает указкой число снаружи круга. Учащиеся молча выполняют соответствующее действие над указанным числом и числом внутри круга и результат показывают на числовом веере. Выигрывает тот ряд, в котором все ученики быстро и правильно показали на числовых веерах результаты.
7 8
+1
-1
5 9 6 4
3 4 2 7
2 9
Дидактическую игру «На 2 больше и на 2 меньше» также можно использовать во время изучения соответствующего материала.
Материал игры: карточки с числами.
Содержание игры. Учитель называет числа в пределах от 2 до 10 и предлагает ученикам в правой руке поднимать число, больше на 2 от данного, а в левой – меньше на 2 от данного. Например, учитель называет число 3, а учащиеся показывают числа 1 и 5. далее учитель называет число 5, а учащиеся показывают числа 3 и 7 и т. д.
Эту же игру можно проводить, предлагая увеличивать и уменьшать числа на 1, на 3, на 4 и так далее.
Дидактические игры, связанные с изучением нумерации чисел второго десятка.
В 1 классе дети изучают не только нумерацию в пределах 10, но и нумерацию чисел 11-20. Учитель продолжает работу по формированию понятия числа, натуральной последовательности чисел, знакомит учащихся с записью и чтением чисел второго десятка, продолжает формирование знаний о по местное значение цифр и десятичный состав чисел, приемы сложения и вычитания, основанные на знании десятичного состава числа, с приемом сложения и вычитания 1, закрепляет умения и навыки учащихся в выполнении сложения и вычитания в пределах 20.
Чтобы сформировать навыки счета в пределах 20, можно использовать игру «Продолжи счет».
Содержание игры. Учитель объясняет учащимся содержание игры, продемонстрировав ее для примера с одним из учеников. Учитель начинает счет (11, 12), ученик продолжает (13, 14...). Далее называет любое число (в пределах изученного материала) и предлагает ученикам (то одному, то другому) продолжить математике. Побеждает тот ученик (ряд учащихся), который не ошибся или допустил меньше всего ошибок. Можно предлагать и в обратном порядке. Важно поднять учеников и дать им возможность показать класса, умеют или не умеют они считать.
Используя дидактические игры уже с первого класса на уроках математики можно заметить, что у первоклассника происходят ощутимые изменения в его мышлении: развивается умение анализировать, обобщать, делать выводы, доказывать целесообразность своих действий.
Итак, мы разработали систему дидактических игр, которые можно использовать на уроках математики в 1 классе. Данная система состоит из четырех подсистем, где каждая из них еще включает игры, связанные с формой их проведения. Все это мы изобразили структурной схеме и подали содержательную характеристику некоторых игр. Соответствующая система игр разрабатывалась с целью проверки ее эффективности в нашем экспериментальном исследовании, о котором мы расскажем в следующем параграфе.
2.3 Результаты экспериментального исследования
В конце эксперимента в экспериментальном и в контрольном классе мы снова провели контроль устных вычислений.
Приводим тексты игр, которые использовались на данном этапе урока.
Игра-эстафета «Заселить» числовые домики
Содержание игры. Ученики каждого ряда выходят и записывают соответствующие числа в числовые домики. Побеждает тот ряд учеников, кто быстро и правильно записал нужные числа.


5
4
3
2
3
4
2
3
1
2
Результаты итогового контроля обобщены в таблице 2
Таблица 2
Правильность ответов учащихся в устных вычислениях в конце года в экспериментальном и контрольном классе
| Классы | Количество учеников (у%) | |||
| Игра «Покажи нужную цифру» | Игра «Будь внимательным» | |||
| Правильно ответили | Неправильно ответили | Правильно ответили | Неправильно ответили | |
| 1‑А экспер. | 57 | 43 | 53 | 47 |
| 1‑В контр. | 27 | 73 | 33 | 67 |
Сравнение последствий проведенного контроля свидетельствует о том, что в экспериментальном классе правильность ответов учащихся в устных вычислениях выросла. Мы объясняем это целенаправленной работой учителя по использованию дидактических игр на уроках математики, которая проводилась в соответствии с задачами формирующего эксперимента.
В ниже приведенных диаграммах приведены ответы учащихся в экспериментальном и контрольном классе в конце эксперимента.
Ответы учащихся приведены на рис. 4 и 5.
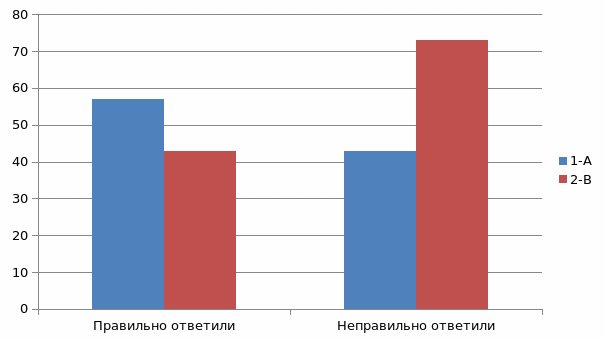
Рисунок 4 – Ответы учащихся на задания в игре «Покажи нужную цифру», количество
Рисунок 5 – Ответы учащихся на задания в игре «Будь внимательным», количество
Итак, из таблиц и диаграмм видно, что большие сдвиги в правильности ответов, учащихся в устных вычислениях течение учебного года состоялись в 1 А классе. Мы объясняем это тем, что ученики 1 А класса обучались по нашей экспериментальной системой (по сравнению с 1 классом, где обучение проходило в обычной форме).
Результаты эксперимента, свидетельствует о том, что предложенная нами система дидактических игр является важным средством повышения общего логического мышления на уроках математики в 1 классе. Практическая реализация предложенной системы позволит повысить общий уровень логического мышления учащихся по математике; обеспечить условия для развития у учащихся интереса к математике и активизировать познавательную деятельность младших школьников.
Выводы по главе 2
Для достижения поставленных задач разработана система дидактических игр.
1. Разработано содержание понятий «дидактическая игра» и «система дидактических игр».
2. Сформулированы требования к проведению дидактических игр:
- проводить игры целенаправленно и систематически на каждом уроке;
- обеспечить условия для проведения игр;
- игровой материал должен соответствовать игре;
- игры должны быть интересными, способствовать развитию учащихся.
3. Сформулированы основные требования к системе дидактических игр:
- система должна способствовать развивающем обучению, оптимальному развитию каждого ребенка в частности;
- система должна обеспечивать рост активности учащихся на уроке;
- игры системы должны быть согласованы с материалом учебника, находиться в зоне доступности ребенка;
- система должна осуществлять пропедевтическую функцию в изучении математики;
- система должна учитывать современные условия школьной практики, быть удобной для работы учителя.
4. Были выяснены вопросы отбора игр на конкретный урок.
5. Система для 1 класса состоит из 28 игр.
Соблюдение указанных требований к системе дидактических игр обеспечивает развитие логического мышления младших школьников.
6. Были решены общие вопросы методики использования дидактических игр.
- Изучены возможности работы с дидактическими играми на разных этапах урока. Сделан вывод, что такие возможности есть практически на всех этапах урока, однако лучшие условия имеет этап устных вычислений. В заключительной части урока можно работать с любыми играми, а на других этапах – только с теми, работа с которыми отнимает относительно мало времени и содержание которых соответствует общей цели работы на данном этапе.
- Испытаны разные формы организации работы с дидактическими играми: Фронтальную, индивидуальную. В частности, было выяснено, в каких случаях целесообразно использование этих форм.
7. Разработана методика использования дидактических игр экспериментальной системы. В контексте конкретных условий класса были созданы четкие и подробные разработки использования игр.
Проведенное теоретическое и экспериментальное исследование, посвященное проблеме использования дидактических игр на уроках математики в начальной школе, позволило решить поставленные задачи и сформулировать основные результаты исследования.
1. Изучая состояние исследуемой проблемы в педагогической теории и практике, мы пришли к следующим выводам.
- Потребность современного общества требует от школы наиболее результативных методов обучения и воспитания, и эта потребность стоит перед начальным звеном школы.
- Проведен анализ научных разработок, учебной и методической литературы, работы учителей начальных классов показывает, что и в теории, и в практике школы проблема использования дидактических игр имеет определенное отражение. Однако на сегодня нет целостного подхода к решению этой проблемы: отсутствует научно обоснованная система дидактических игр и методика их использования в начальной школе.
2. Поиски эффективной системы использования дидактических игр на уроках математики побудили нас к изучению психолого-педагогических условий их использования. Была проанализирована концепция развивающего обучения, выделены соответствующие особенности детской психики. На основе анализа психолого-педагогических условий использования дидактических игр на уроках математики были сформулированы требования к методике их проведения:
- методика должна руководствоваться принципом полной реализации возрастных познавательных возможностей детей;
- она должна обеспечивать вариативность условий, в которых протекает работа учителя и ученика;
- методика должна способствовать оптимальному развитию каждого школьника;
- обучение по данной методической системе должно обеспечивать каждому ученику физическое и психологическое здоровье.
3. Для достижения поставленных задач разработана система дидактических игр.
1) Разработано содержание понятий «дидактическая игра» и «система дидактических игр».
2) Сформулированы требования к проведению дидактических игр:
- проводить игры целенаправленно и систематически на каждом уроке;
- обеспечить условия для проведения игр;
- игровой материал должен соответствовать игре;
- игры должны быть интересными, способствовать развитию учащихся.
3) Сформулированы основные требования к системе дидактических игр:
- система должна способствовать развивающему обучению, оптимальному развитию каждого ребенка в частности;
- система должна обеспечивать рост активности учащихся на уроке;
- игры системы должны быть согласованы с материалом учебника, находиться в зоне доступности ребенка;
- система должна осуществлять пропедевтическую функцию в изучении математики;
- система должна учитывать современные условия школьной практики, быть удобной для работы учителя.
4) Были выяснены вопросы отбора игр на конкретный урок.
5) Система для 1 класса состоит из 28 игр.
Соблюдение указанных требований к системе дидактических игр обеспечивает разносторонность условий для математического развития младших школьников.
4. Были решены общие вопросы методики использования дидактических игр.
- Изучены возможности работы с дидактическими играми на разных этапах урока. Сделан вывод, что такие возможности есть практически на всех этапах урока, однако лучшие условия имеет этап устных вычислений. В заключительной части урока можно работать с любыми играми, а на других этапах – только с теми, работа с которыми отнимает относительно мало времени и содержание которых соответствует общей цели работы на данном этапе.
- Испытаны разные формы организации работы с дидактическими играми: фронтальная, индивидуальная. В частности, было выяснено, в каких случаях целесообразно использование этих форм.
5. Разработана методика использования дидактических игр экспериментальной системы. В контексте конкретных условий класса были созданы четкие и подробные разработки использования игр.
6. Комплексный подход к занятиям с дидактическими играми системы, проведение формирующего эксперимента позволили определить эффективность системы обучения. Результативность исследования оценивалось на основе использования учителями дидактических игр; сравнение результатов начального и конечного контроля в экспериментальном и контрольном классе; бесед и наблюдений. Результаты эксперимента показали, что практическая реализация предложенной системы позволяет:
- повысить уровень логического мышления учащихся на уроках математики;
- повысить общий уровень знаний по математике;
- развивать интерес учащихся к математике.
Обучение учащихся с использованием дидактических игр значительно повысит уровень знаний не только сильных учеников, но и средних и даже слабых.
Подытоживая в целом, отметим: поставленные задачи решены, цель исследования достигнута, гипотеза подтверждена
-
Аникеева, Н.П. Воспитание игрой: Книга для учителя. – М.: Просвещение, 1987.
-
Байрамукова П.У., Джулай А.М. Обучение математике в начальных классах: практические и лабораторные занятия. Ростов –на –Дону. Феникс. 2007.
-
Болотина, Н.И. Дидактическая игра – одно из средств активизации познавательной деятельности детей шестилетнего возраста // Начальная школа. – 2012. – №12. – С. 42-44.
-
Вапняр, Н.Ф. Использование математических игр на уроке // Начальная школа. – 2015. – №3.
-
Грабская, И.А., Киричук А.И. Игровые формы психологической коррекции: Использование игровых упражнений в развитии внимания школьников // Советская школа. – 1990. – №12. – С. 59-64.
-
Гримакова, Г.Н., ЮсубоваИ.Б. Развитие познавательной самостоятельности школьника в игровой деятельности // Начальная школа. – 2014. – №11. –С. 41-45.
-
Гуцан, Л. Игра как средство пропедевтической профориентационной работы // Начальная школа. – 2015. – №9. –С. 51-53.
-
Денис, С.А. Дидактические игры // Начальная школа. – 2014. – №10.
-
Жорник А. Формирование познавательной деятельности учащихся в процессе совместной игровой деятельности // Родная школа. – 2010. – №3. –С. 37-39.
-
Земцева, Л.И., Сушкова Е.Ю. Роль дидактической игры на уроках математики // Начальная школа. – 2016. – №10.
-
Казакова, А.Г. Дидактические игры на уроках математики // Начальная школа. – 2013. – №5.
-
Кларин, М.В. Игра в учебном процессе [начальной школы]. Сов. Педагогика. - 1985. – №6. –C. 57–61.
-
Козлова, Е.А. Роль современных дидактических игр в развитии познавательных интересов и способностей младших школьников /Начальная школа. – 2014. – №11. –С. 49-52.
-
Колосов, П. Место учебной игры в методической системе современной дидактики // Родная школа. – 2016. – №11. –С. 65-66.
-
Кравцова, Е.Е. Методологическое значение взглядов Д.Б. Эльконина на детскую игру // Мир психологии. – 2017. – №1.–С. 68-76.
-
Кудикина, Н.В. Ретроспективный взгляд на формирование современной модели игровой деятельности // Путь образования. – 2013. – №1. –С. 46-49.
-
Личностные особенности развития интеллектуально одаренных младших школьников. Прометей. Мякишева Н.М. 2014г.http://www.iprbookshop.ru/8308.html
-
Маслюкова, Т.А. Дидактические игры на уроках математики // Начальная школа. – 2015. – №2. – С. 52-54.
-
Мацко, Н.Д., Никитинская Н.И. Игровая деятельность учащихся на уроках математики // Начальная школа. – 2013. – С. 126.
-
Мельничук, А.И. Дидактические игры как средство адаптации шестилетнего ребенка к обучению и воспитанию //Начальная школа. – 2015. – №16-18. –С. 2-6.
-
Методика преподавания дисциплин естественнонаучного цикла. Современные проблемы и тенденции развития. Омская юридическая академия. Агалаков С.А., Бабичева И.В., Болдовская Т.Е., Берникова И.К., Борзенко Е.К., Еремин А.М. 2015г.
http://www.iprbookshop.ru/29824.html
-
Общие вопросы методики обучения математике в начальных классах. Амурский гуманитарно-педагогический государственный университет. Алексеева О.В. 2015г.http://www.iprbookshop.ru/22283.html
-
Пахно, Т.И. элементы игры на уроках математики // Начальная школа. – 2011. – №5.
-
Рыжук, В.И. Игра как метод обучения и воспитания // Начальное обучение и воспитание. – 2015. – №16-18. – С. 20-25.
-
Рудакова, Т.И. Дидактическая игра – действенное средство активизации познавательной активности учащихся // Начальное обучение и воспитание. – 2015. – №16-18. –С. 7-13.
-
Сопко, И.П. Игровые способы в обучении шестилеток // Начальная школа. – 2012. – №3. –С. 39-40
-
Стольникова, С. Детская игра под углом зрения психолога // Начальное образование. – 2013. – №38. – С. 7.
-
Ушинский, К.Д. Избранные педагогические произведения. – М.: Советская школа, 1949, С. 213.
-
Федусенко, Ю. Особенности влияния учебно-игровой деятельности на развитие основных психических процессов в младшем школьном возрасте // Родная школа. – 2015. – №4. – С. 25.
-
Фок,А.В., Смолень Г.И. Роль игры в формировании нравственных качеств и взаимоотношений // Начальная школа. – 2017. – №2. – С. 25.
-
Царева С.Е. Методика преподавания математики в начальной школе: Учеб. для вузов. - М.: Академия, 2014. -496с. -
-
Щербань, П. Дидактические игры в учебно-воспитательном процессе // Начальная школа. – 2013. – №9. – С. 18-20.
-
Шадрина И.В. Методика преподавания начального курса математики. М. Юрайт. 2018г.
ПРИЛОЖЕНИЯ
Приложение 1
Урок нового поколения.
Тема: Порядковый счет. Неделя.
Цель: Объяснить учащимся, чем отличаются ответы на вопрос «сколько» и «который», научить употреблять порядковые числительные. Познакомить с понятием «неделя» и названиями дней недели. Развивать логическое мышление. Формировать навыки счета.
Оборудование: Демонстрационный материал: картинки, предметные картинки, игрушки, цифровая касса, таблицы.
Ход урока
1) Организационный момент.
- Добрый день, в добрый час!
Рада, дети, видеть вас!
Все вы услышали звонок?
Он позвал вас на урок.
Каждый из вас приготовился,
на перерыве постарался.
Сейчас сядут все девочки,
А за ними все мальчики.
- Сейчас мы с вами начнем урок математики.
Математика – наука
Точная и серьезная.
И прожить нам без нее,
Даже дня нельзя.
2) Повторение изученного материала.
а) Опрос по технологии «Микрофон»
- Посчитайте от 1 до 6; от 6к 1.
- Назовите « соседей» числа 5;
- Какое число при счете предшествует числу 3?
- Какое число следует за числом 6?
б) Интересные задачи
Кошка Мурка на все ножки
Надела шелковые чулочки.
И один где-то потерялся.
Сколько на кошке осталось? (3)
Мчатся на санках
Четверо малышей.
Трое из них – девочки.
Сколько же здесь мальчиков? (1)
3) Изучение нового материала.
а) Работа с демонстрационным материалом
На наборном полотне картинки: груша, яблоко, слива, вишня, малина.
- Что вы видите на доске? Как можно назвать одним словом? (фрукты)
- Посчитайте, сколько всего фруктов?(5)
- Какой фрукт стоит на первом месте? На втором?
- На котором месте стоит слива? Вишня?
- Что стоит последним?
Слова указывают на порядок размещения предметов. Мы называли фрукты слева направо.
Для того, чтобы правильно определить порядковый номер предмета, надо знать, в каком порядке нужно перечислять. Если направление не указывается, то считают слева направо.
б) Работа с печатной тетрадью.
- Посчитайте предметы слева направо и справа налево. Сколько всего?
- Рассмотрите вторую задачу. Кого вы видите на рисунке? Которая за порядком бабушка, если считать слева направо? справа налево? Сколько всего людей?
- Которые по порядку Пес, Петух, Осел, если считать слева направо? справа налево? Сколько всего животных?
- Практическое задание. Раскрась третий слева и четвертый справа котиков.
в) Игра «Поезд»
Содержание игры. Учитель поочередно вызывает к доске учеников. Каждый из них, выполняя роль вагона, называет свой номер. Первый вызванный ученик говорит: «Я – первый вагон». Второй ученик выполняет роль второго вагона, он называет свой порядковый номер и т.д. Затем дети поворачиваются в другую сторону – последний вагон становится первым. Дети называют свои порядковые номера справа налево.
4) Физкультминутка.
Встанем, дети, ровненько.
Вот так! Вот так!
Поклонимся низко.
Вот так! Вот так!
Далее руки в стороны,
Веселенько пойдем в пляски!
Так все прыг! прыг!
А ножками диб! диб!
Вверх ручки поднимай.
И все вместе приседай!
Станем вновь ровненько!
а) Работа с печатной тетрадью (продолжение)
Загадка.
Семь братьев возрастом равные, именами разные. (Дни недели)
- Дети, кто скажет сколько дней в неделе?
- А как эти дни называются?
- С какого дня начинается неделя?
- Какая по порядку среда? суббота?
- Что же помогает следить за сменой дней недели?
- Закрасьте пятый слева листок календаря. Какой день недели он показывает? День перед этим днем? за этим днем?
Стихотворение про дни недели.
Семеро детей в неделе –
Вот семейка удивительная,
Никак не может папа
Всех до кучи посчитать.
Понедельник где-то путешествует
И кота в мешке бдит.
А вторник со средой
Носят решето с водой,
А четверг идет к пятнице
Отведать маслица.
Довольна суббота,
Аж кипит у всех работа.
Вместе все ушли обрадованные
Отдохнуть до воскресенья.
- Дети, давайте еще раз повторим названия дней недели. Я называю порядковый номер, а вы – день недели, который ему соответствует.
(первый – понедельник, второй – вторник и т. д.)
Упражнение на логическое мышление. Задание 8.
б) Игра «Будь внимателен»
Сколько лапок у волков? (4)
Сколько у мышки есть хвостов? (1)
Сколько ушек у зайцев? (2)
Сколько пальцев на руке? (5)
Сколько крыльев у лисы? (Нисколько)
Сколько в тереме колодцев? (Нисколько)
Сколько лягушек летает в небе? (Нисколько)
Сколько хвостиков у тебя? (Шутка)
в) Игра «Найди соседей»
- На доске – таблицы с геометрическими фигурами:


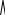







Ученики выкладывают карточки с нужными цифрами.
г) Игра «Что изменилось?»
Учитель ставит на столе 5 игрушек: заяц, медведь, волк, лиса, еж. Ученики называют: первый – заяц, второй – медведь и т. д. Затем ученики закрывают глаза, а учитель переставляет игрушки местами. Ученики открывают глаза и рассказывают, что изменилось.
д) Игра «Что лишнее»



- Какая фигура лишняя? (треугольник)
-Какой порядковый номер она имеет? (Пятый)
5) Физкультминутка.
Буратино потянулся,
Раз – нагнулся, два – нагнулся,
Руки в сторону развел –
Пожалуй, ключик потерял.
А чтобы ключик отыскать.
Надо нам цыпочки встать.
6) Работа в парах.
На каждую парту учитель кладет конверт с рисунками грибов, читает стихотворение, а дети, работая в парах должны выполнять указание учителя, то есть правильно выложить грибы.
Шесть грибовЛаураимела
И на стол их разложила.
Первый гриб – дождевик,
Под дождем расти он привык.
Подберезовик – это два,
Круглая у него голова.
Рыжик – третий, он рыжий,
Съедобный, да еще и вкусный.
А четвертый – боровик,
Он – веселый шутник.
Сыроежка будет пятая,
Только чуть-чуть примятая.
Шестой очень подозрительный,
Хоть красный, словно спелый.
Белые крапинки, он имеет:
Мухомора каждый знает!
Он ядовитый, опасный
И к столу неуместный.
(В конце упражнения учащиеся еще раз называют в какой последовательности расположены грибы).
7) Итог урока. (Дети отвечают по технологии «Микрофон»)
- Дети, что мы сегодня изучили на уроке?
- Что вам больше всего понравилось?
- Посмотрите на своего соседа по парте, улыбнитесь друг другу и скажите:
- Я – молодец!
- Ты – молодец!
- Мы все – молодцы!
Вот и прозвучал звоночек –
Закончился наш урок,
За работу по заслугам,
Спасибо вам, друзья!
Приложение 2
Учимся взвешивать. Килограмм. 1 класс
Тема: Единицы измерения массы. Килограмм.
Цель: Ознакомить учеников с единицей измерения массы -1 килограмм. Показать практическое использование этой единицы. Углубить умения решать примеры и задачи. Развивать творческое мышление.
Оборудование: таблицы, весы, гири, хлеб, сахар, крупа, яблоки.
Ход урока.
1) Организационный момент.
Раздался школьный звонок,
Начинаем урок.
Будем работать старательно,
Чтобы услышать в конце,
Чтобы в нашем 1 классе
Дети – просто молодцы.
- Дети, у нас сегодня очень интересный урок. Мы будем играть в разные игры. Но для этого нам нужно пригласить на урок такие слова: «внимательность», «исполнительность» и «память» (учитель на доске прикрепляет эти слова)
внимательность
память
исполнительность
2) Повторение и закрепление изученного материала.
Устный счет.
а) Задачи – стихи.
• Быстро едет Федор
На велосипеде,
А за ним – еще пять ребят.
Сколько ребят едет в сад? (1+5)
• У Имашки три копейки,
А Заремаимеет пять.
Поможем девочкам
Деньги все посчитать. (3+5)
б) Найти примеры с ответом 9.
4+5
8+0
10-1
6+3
10-4
Математический диктант.
Первое слагаемое 4, второе 6. Вычислите сумму.
На сколько 6 больше 4?
На сколько 3 меньше 7?
8 увеличить на 1.
5 уменьшить на 2.
3) Изучение нового материала.
а) Беседа
- Все предметы имеют разную массу. Возьмите в одну руку учебник, а в другую карандаш. Что тяжелее? Что легче? В этом случае говорят, что масса учебника больше массы карандаша. Разные предметы имеют разную массу. Массу определяют взвешиванием. Чтобы измерить величину, надо знать единицу ее измерения. Одной из единиц измерения массы является килограмм. Взвешивают килограммами на весах. Весами пользуются в магазинах, на базаре.
- Кто работает в магазине? (Продавцы)
- Как зовут тех людей, которые покупают товары? (Покупатели)
б) Игра «Магазин»
Чтобы взвесить товар продавцы имеют весы и гири.
- Давайте взвесим на весах пакет с крупой. На левую чашу кладем пакет с крупой, а на правую – гири. Гири бывают весом 1 кг, 2кг,5 кг. На письме слово килограмм записывают сокращенно: 1кг,2кг,3кг.
- Итак , ставим столько гирь, чтобы весы уравновесились. Какую массу имеют гири, такую и крупа.
- А теперь взвесим буханку, учебник, яблоки. (Дети выступают в роли продавцов и покупателей)
в) Работа в тетрадях.
- Каллиграфическая минутка: прописать 1кг, 2 кг, 5кг.
- Решение примеров
10-6+4 8-4+2 3+7-8 9-4+3
4) Физкультминутка
Ноги шире, руки в стороны -
Лес сошел в короткие сроки.
Ветра леса не сломать.
Для зверей лес – пища и дом.
Ветви – руки подняли,
Солнцу дань уважения отдали.
А землице поклонились,
Ветвями вниз наклонились.
5) Работа с учебником.
а) Задание №1
Рассмотрите рисунок и скажите, какая масса риса и какая масса гранатов.
б) Решение задачи по технологиям «Два – четыре – все вместе», «Микрофон».
Мальчик поймал 5 окуней, а девочка – на 2 окуни меньше. Сколько окуней поймала девочка? Сколько окуней поймали дети вместе?
Учитель изучает условие задачи с учащимися по обычной методике(2мин), потом говорит:
Подумайте, и решите задачу сначала самостоятельно (1мин), затем обсудите с соседом по парте(1мин), а затем в четверках (1мин). После этого один ученик из четверки представляет решение задачи с помощью технологии «Микрофон».
После того, как ученики пришли к общему решению, учитель предлагает кому-то из детей записать задачу на доске, а остальные в тетрадях.
в) Сравнение выражений и числа по технологии «Работа в парах».
Учитель предлагает самостоятельно выполнить задание, а потом объединиться в пары с соседом по парте и сделать взаимопроверку.
7

 +3 9 9-4 6 4+4 10
+3 9 9-4 6 4+4 10
9

 -2 7 9-3 5 5+5 9
-2 7 9-3 5 5+5 9
Представление результатов с помощью технологии «Микрофон».
6) Закрепление изученного материала.
а) Составление выражений и задач по рисунку.





1кг 3кг 2кг ? 4кг?
Какова масса двух куриц?
- На сколько масса индюка больше массы курицы? А масса двух куриц? (одинакова)
- Составьте задачу. Которая бы решалась так: 3+1=
Масса кота 1кг, масса кролика 3 кг. Какова масса кота и кролика вместе?
| 4 |
|
|
| 9 | 5 |
|
|
|
| 6 |
| 4 |
|
|
|
| 5 |
|
|
| 1 | 6 |
7) Итог урока.
- Что мы сегодня изучали на уроке? (Килограмм)
- В какую игру мы с вами играли? (Магазин)
- Какие слова мы пригласили на урок? (усидчивость, память,внимательность)
- Вы сегодня хорошо постарались, были внимательными и хорошо запомнили материал, поэтому эти слова вам подготовили разные интересные загадки.
- Итак, загадка от «внимательности»
На крыльце играли пять мышек. Прибежала кошка и села на крыльце. Сколько зверей стало? (Одна кошка, потому мышата убежали)
- Загадка от «усердия»
Еж весит 1кг, а заяц – на 5кг больше. Сколько весит заяц? (6 кг)
- Загадка от «памяти»
- Что тяжелее: 1кг муки или 1кг железа? (масса одинаковая)
- А сейчас к вашему вниманию изюминка.
Курица говорит петуху: «Дружище,
Вижу ты поправилась очень...»
Петух согласился: «Угу ».
И поплелся на вес.
Стал Петька двумя ногами
И затянул два килограмма.
- Ого - го,- крикнул, - а ну,
Состояния только на одну...
Сколько сейчас петух весит? (тоже три).
45
© 2023, Мациева Амнат Султановна 2450 20
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Полезное для учителя




 + = 7
+ = 7





















