ИСПОЛЬЗОВАНИЕ ПРОБЛЕМНОЙ ЛЕКЦИИ КАК СРЕДСТВА ДИАЛОГИЧЕСКОГО ОБЩЕНИЯ С ОБУЧАЕМЫМИ
Белоусова О. П.
«Лицей №13» (г. Троицк)
Реализация компетентностного подхода предусматривает широкое использование в учебном процессе активных и интерактивных форм проведения занятий (семинаров в диалоговом режиме, дискуссий, деловых и ролевых игр, разбор конкретных ситуаций и т.п.) в сочетании с внеклассной работой, с целью формирования метапредметных обучающихся. Одной из основных активных форм обучения является лекция с проблемным изложением материала.
Проблемное изложение знаний осуществляется на основе создания и разрешения проблемных ситуаций, т.е выдвижением в процессе обучения спорных положении, различных вариантов решения той или иной задачи, а также вовлечением обучаемых в активное обсуждение поставленных проблем и принятие совместных решений [2].
Проблемная лекция позволяет отвлечь учащихся от механического конспектирования излагаемого материала и привлечь их к активной познавательной деятельности. В отличие от информационной лекции, на которой преподносится и объясняется готовая информация, подлежащая запоминанию, на проблемной лекции новое знание вводится как неизвестное, которое необходимо «открыть». Создав проблемную ситуацию, учитель побуждает учащихся к поиску решения проблемы, постепенно подводя их к искомой цели. Поэтому целесообразно, чтобы поставленные в процессе чтения лекции проблемы не объяснялись тут же самим учителем, а их решение определялось в процессе обсуждения, и к выводам ученик пришёл самостоятельно [5].
Общий эффект проблемной лекции определяется её содержанием, способом организации совместной деятельности и теми средствами общения, которые обеспечивают эффективную «трансляцию» материала. Диалогическое общение по ходу изложения материала улучшает усвоение, положительно влияет на мотивационную сферу познавательной деятельности, побуждает к совместному размышлению, вскрывает логику разрешения противоречий, а в итоге является необходимым условием для развития логического и критического мышления обучаемых [4]. Диалог предполагает выявление отношения ученика к обсуждаемой проблеме. Правильно построенный диалог создаёт атмосферу взаимопонимания, доверия, позволяет ученикам приобретать умение чётко формулировать и излагать свои мысли [6].
Чтобы сделать общение на уроках диалогическим, учителю необходимо прежде всего учитывать эмоциональное состояние обучаемых, опираться на положительное в них, создавать ситуацию успеха, проявлять живой интерес к взаимному обмену информацией. Целесообразно также, чтобы даже в недостаточно чётком решении учитель находил рациональное звено, акцентировал на нём внимание и, тем самым, поощрял ученика к дальнейшей активности. Основная задача лектора состоит не столько в передачи информации, сколько в приобщении обучаемых к объективным противоречиям. «Сотрудничая» с проблемой, ученики открывают для себя новые знания. Этим усиливается тенденция планировать обучение как творческий процесс, не сводимый к освоению готовых правил решения разнообразных задач [1].
Для создания проблемных ситуаций при обучении математике мы используем прикладные задачи или их отдельные фрагменты. Задачи подбираются так, чтобы их постановка привела к необходимости приобретения учащимися новых знаний.
Приведём фрагмент лекции с проблемной ситуацией по теме «Второй замечательный предел», которая начинается с постановки прикладной задачи.
Учитель: Представьте такую ситуацию. Первоначальный вклад в банк составляет Q0 рублей. Банк выплачивает ежегодно р % годовых. Найдите размер вклада Q через t лет.
Ученик: Очевидно, при р% годовых размер вклада ежегодно будет увеличиваться в (1+р/100) раз, тогда получим:
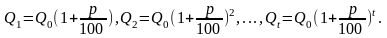
Учитель: А если проценты по вкладу начисляются не один раз в году, а n раз?
Ученик: При том же ежегодном приросте р% начисления за (1/n) часть года составит (p/n) %, а размер вклада за t лет при m начислениях составит
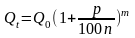
Учитель: Какие возможны значения n?
Ученик: Если проценты по вкладу начисляются каждое полугодие, то n=2, ежеквартально - n=4, ежемесячно - n=12, ежедневно - n=365.
Учитель: А чаще?
Ученик: Каждый час, т.е. n=8760, каждую минуту, каждую секунду и т.д.
Учитель: Итак, мы пришли к выводу, что теоретически проценты могут начисляться непрерывно, тогда 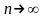 . Чему же при этом размер вклада будет равен за t лет?
. Чему же при этом размер вклада будет равен за t лет?
Ученик: размер вклада за t лет будет равен:
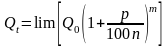 .
.
Учитель: Вычислите данный предел.
Ученик: Так как Q0 от n не зависит, вынесем его за знак предела. Имеем:
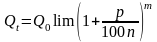 .
.
При 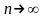 имеем в данном случае неопределенность
имеем в данном случае неопределенность 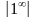 . (пытаются применить известные методы раскрытия неопределённостей, которые не приводят к желаемому результату).
. (пытаются применить известные методы раскрытия неопределённостей, которые не приводят к желаемому результату).
Возникла проблема как следствие противоречия между пониманием научной важности рассматриваемой задачи и отсутствием теоретической базы для её решения.
Учитель: Итак, в результате рассмотрения данной задачи о непрерывном начислении процентов возникла необходимость раскрытия неопределённости 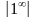 . Изученными ранее методами этого сделать нельзя. Поэтому мы рассмотрим новое понятие – «второй замечательный предел», которое нам поможет в вычислении аналогичных пределов и изучении метода раскрытия неопределённости
. Изученными ранее методами этого сделать нельзя. Поэтому мы рассмотрим новое понятие – «второй замечательный предел», которое нам поможет в вычислении аналогичных пределов и изучении метода раскрытия неопределённости 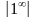 . В итоге получена формула непрерывного начисления процентов:
. В итоге получена формула непрерывного начисления процентов:
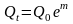 .
.
Далее целесообразно предложить учащимся оценить погрешность вычисления суммы вклада по полученной формуле непрерывного начисления процентов и по формуле сложных процентов Qt=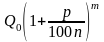 и сделать соответствующие выводы.
и сделать соответствующие выводы.
В результате, такое общение в виде диалога направлено на поддержание познавательной, мыслительной активности обучаемых. Начав с якобы нерешенной задачи, учитель создаёт проблемную ситуацию, формируя в сознании обучаемых мотив овладения рубежом научного знания. Серия вопросов трансформирует проблему в модель поиска её решения, где рассматриваются различные пути, средства и методы решения. Решение проблемы требует творческого мышления.
В статье, на примере фрагмента лекции с проблемной ситуацией, по теме «Второй замечательный предел», говорится об использовании метода диалогизации, как средстве общения учителя с обучаемыми.
Список использованной литературы:
-
Бодалёв А.А. О взаимосвязи общения и отношения // Вопросы психологии. 1994. №1, с. 24
-
Вербицкий А.А. Активное обучение в высшей школе: контекстный подход: метод. пособие. – М.: Высшая школа, 1991. – 207с., -с.93-94.
-
Зимняя И.А. Педагогическая психология. М., 1999.,С.324
-
Горшкова В.В. Проблема субъекта в педагогике. Учебное пособие к спецкурсу. – Л., 1991. – 77с, c.18
-
Зимняя И.А. Педагогическая психология. М., 1999.,c.324 – c.288-289.
-
Коротаева Е.В. Основы педагогического взаимодействия. Екатеринбург, 1996. – 183с., с.54.







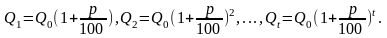
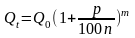
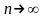 . Чему же при этом размер вклада будет равен за t лет?
. Чему же при этом размер вклада будет равен за t лет?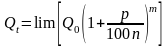 .
.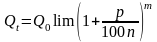 .
.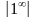 . (пытаются применить известные методы раскрытия неопределённостей, которые не приводят к желаемому результату).
. (пытаются применить известные методы раскрытия неопределённостей, которые не приводят к желаемому результату).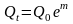 .
.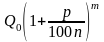 и сделать соответствующие выводы.
и сделать соответствующие выводы. 



















